Statistical Notes
Miscellaneous statistical stuff
- Critiques
- “Someone Should Do Something”: Wishlist of Miscellaneous Project Ideas
- Estimating Censored Test Scores
- The Traveling Gerontologist Problem
- Bayes Nets
- Genome Sequencing Costs
- Proposal: Hand-Counting Mobile App for More Fluid Group Discussions
- Air Conditioner Replacement
- Some Ways of Dealing With Measurement Error
- Value of Information: Clinical Prediction Instruments for Suicide
- Bayesian Model Averaging
- Dealing With All-Or-Nothing Unreliability of Data
- Dysgenics Power Analysis
- Power Analysis for Racial Admixture Studies of Continuous Variables
- Operating on an Aneurysm
- The Power of Twins: Revisiting Student’s Scottish Milk Experiment Example
- RNN Metadata For Mimicking Individual Author Style
- MCTS
- Candy Japan A/B Test
- DeFries-Fulker Power Analysis
- Inferring Mean IQs From SMPY/TIP Elite Samples
- Genius Revisited: On the Value of High IQ Elementary Schools
- Great Scott! Personal Name Collisions and the Birthday Paradox
- Detecting Fake (Human) Markov Chain Bots
- Optimal Existential Risk Reduction Investment
- Model Criticism via Machine Learning
- Proportion of Important Thinkers by Global Region Over Time in Charles Murray’s Human Accomplishment
- Program for Non-Spaced-Repetition Review of past Written Materials for Serendipity & Rediscovery: Archive Revisiter
- On the Value of New Statistical Methods
- Bayesian Power Analysis: Probability of Exact Replication
- Expectations Are Not Expected Deviations and Large Number of Variables Are Not Large Samples
- Oh Deer: Could Deer Evolve to Avoid Car Accidents?
- Evolution As Backstop for Reinforcement Learning
- Acne: a Good Quantified Self Topic
- Fermi Calculations
- Selective Emigration and Personality Trait Change
- The Most Abandoned Books on GoodReads
- Best Student Ever!
- Little’s Law in the Wild
- Tail Collapse
Critiques
criticism of teeth-removal experiment in rats https://www.lesswrong.com/r/discussion/lw/kfb/open_thread_30_june_201411ya_6_july_201411ya/b1u3
criticism of small Noopept self-experiment http://www.bluelight.org/vb/threads/689936-My-Paper-quot-Noopept-amp-The-Placebo-Effect-quot?p=11910708&viewfull=1#post11910708
why Soylent is not a good idea https://www.lesswrong.com/lw/hht/link_soylent_crowdfunding/90y7
misinterpretation of fluoridation meta-analysis and ignorance of VoI http://theness.com/neurologicablog/index.php/anti-fluoride-propaganda-as-news/#comment-76400
https://www.lesswrong.com/lw/1lt/case_study_melatonin/8mgf
Fulltext: is this possible? http://nextbigfuture.com/201411ya/05/kl-vs-gene-makes-up-six-iq-points-of.htmlNootropics/comments/25233r/boost_your_iq_by_6_points/chddd7f
tACS causes lucid dreaming: https://www.reddit.com/r/LucidDreaming/comments/27y7n6/no_brain_stimulation_will_not_get_you_lucid/ck6isgo
Herbalife growth patterns: https://www.reddit.com/r/business/comments/24aoo2/what_unsustainable_growth_looks_like_herbalife/ch5hwtv
Plausible correlate of Fairtrade: https://www.reddit.com/r/Economics/comments/26jb2d/surprise_fairtrade_doesnt_benefit_the_poor/chrx9s4
slave whippings vs cotton production https://www.lesswrong.com/r/discussion/lw/kwc/open_thread_sept_17_201411ya/bajv
whether a study on mental illness & violence shows schizophrenics are not more likely to murder but rather be murdered: https://www.reddit.com/r/psychology/comments/2fwjs8/people_with_mental_illness_are_more_likely_to_be/ckdq50k / http://www.nationalelfservice.net/publication-types/observational-study/people-with-mental-illness-are-more-likely-to-be-victims-of-homicide-than-perpetrators-of-homicide/#comment-95507 (see also http://slatestarscratchpad.tumblr.com/post/120950150581/psycholar-giraffepoliceforce-museicetc https://www.reddit.com/r/slatestarcodex/comments/744rqn/violence_is_not_a_product_of_mental_illness/dnwb1kj/ )
Fortune analysis of higher female CEO returns https://www.lesswrong.com/r/discussion/lw/l3b/contrarian_lw_views_and_their_economic/bftw
algae/IQ: https://www.lesswrong.com/r/discussion/lw/l9v/open_thread_nov_17_nov_23_201411ya/bm7o
synaesthesia/IQ: https://www.reddit.com/r/psychology/comments/2mryte/surprising_iq_boost_12_in_average_by_a_training/cm760v8
misinterpretation: https://slatestarcodex.com/201411ya/12/08/links-1214-come-ye-to-bethlinkhem/
underpowered/multiple-correction jobs program: https://slatestarcodex.com/201411ya/12/08/links-1214-come-ye-to-bethlinkhem/
claimed fall in digit span backwards minuscule and non-statistically-significant, no evidence of heterogeneity beyond variability due to sample size https://drjamesthompson.blogspot.com/2015/04/digit-span-bombshell.html?showComment=1428096775425
Claimed randomized experiment of whether sushi tastes worse after freezing is not actually a randomized experiment https://www.reddit.com/r/science/comments/324xmf/randomized_doubleblind_study_shows_the_quality_of/cq8dmsb
sexual openness result undermined by ceiling effect http://mindhacks.com/2015/04/28/when-society-isnt-judging-womens-sex-drive-rivals-mens/
music study claiming WM interaction: possible ceiling effect? see FB PM
attempt to measure effect of Nazi anti-schizophrenia eugenics program failed to use breeder’s equation to estimate possible size of effect, which is too small to detect with available data and hence attempt is foredoomed: https://rpubs.com/JLLJ/GSCZ
claim high IQ types almost 100% failure rates due to inappropriate model assumption of normal distribution + narrow standard deviation: https://polymatharchives.blogspot.com/2015/01/the-inappropriately-excluded.html?showComment=1441741719623
implausible claims about success rate of facial recognition applied to St Petersburg population: https://news.ycombinator.com/item?id=11491264 (see also “Facial recognition systems stumble when confronted with million-face database”)
human Toxoplasma gondii study is not well-powered as authors claim due to incorrect power analysis, and results are evidence for harm: https://blogs.discovermagazine.com/neuroskeptic/2016/02/20/myth-mind-altering-parasite-toxoplasma-gondii/
attempt at attributing Bitcoin price increases to technology improvements: https://www.reddit.com/r/Bitcoin/comments/5tbt8f/buzz_factor_or_innovation_potential_what_explains/ddlmzrz/
analysis of designer drug/research chemical activity on Wikipedia is driven almost entirely by editing patterns of just 2 Wikipedia editors particularly interested in the topic: http://calib.ro/chemical-wiki/explorations/2016-09-12-emcdda-watchlist-and-wikipedia-timeline#comment-3277669328
failure to use mediation SEM, difference-in-statistical-significance-is-not-a-significant-difference: https://www.reddit.com/r/slatestarcodex/comments/6qwb0q/critical_thinking_skills_are_more_important_than/dl51ubw/
Neanderthal ancestry percentage & autism: https://www.reddit.com/r/slatestarcodex/comments/74fevz/findings_suggest_that_high_levels_of_neanderthal/dny3sh9/
Anime image classification project likely undone by using non-i.i.d. images
Failed Facebook Critiques
Facebook emotion study: https://www.reddit.com/r/psychology/comments/29vg9j/no_emotions_arent_really_contagious_over_facebook/cip7ln5
A reply to http://www.ischool.berkeley.edu/newsandevents/news/20140828facebookexperiment (too long for inclusion in https://news.ycombinator.com/item?id=8378743 )
91 points and no comments? OK, I guess it falls to me to jump on this grenade.
So why is the Facebook study bad science? After 5 screens of meandering anecdotes, insinuations, insults, etc we finally get to a real criticism:
Did people feel betrayed about the lack of informed consent? You know, in psychology research, when people find out they’ve been an unwitting experimental subject, it’s not uncommon for them to feel duped. They’re at least surprised. The only distinction is that academics who experiment on subjects without getting their consent first usually tell people about it immediately afterward. They debrief the subjects and answer questions. They unruffle ruffled feathers. They may allow a subject to remove his or her data from the experiment. In some cases, they even offer follow-up services. Given that Facebook did nothing to inform subjects or make them feel whole again, it’s hard to blame folks for feeling unduly violated.
So? As was pointed out, these experiments are run all the time by all sorts of entities, and by making this criticism you are implicitly arguing that it would be better for Facebook to keep the results secret (like companies usually do) instead of informing us about very relevant results in the brave new world of the Internet. Far from arguing for good science, OP is arguing for bad science as somehow ‘ethical’. (This is quite aside from the issue that informed consent makes no sense and was a kneejerk reaction to abuses that didn’t need the invention of scholastic concepts like ‘informed consent’.)
The experiment also forced many people to contemplate, for the first time, the kind of persuasive power Facebook might surreptitiously wield around the world given its size and scale.
Also not a reason for it being ‘bad science’.
On the other side of the firestorm were people who couldn’t see how the experiment was any different from your run-of-the-mill psychology experiment. Or, alternatively, how it was different from the widespread Internet practice of A/B testing, where you experiment with different variations of a website to see which is most effective at persuading visitors to buy, or download, or whatever the site’s goal is. Some of these experiments feel blatantly manipulative, like the headlines that are constantly tested and retested on visitors to see which ones will get them to click. We have a word for headlines like this: “click-bait.” But nobody ever hands out consent forms.
Oh good, so the author isn’t a complete idiot.
The every-which-way quality of the reaction, I think, comes in part from the fact that the study crossed academic and corporate boundaries, two areas with different ethical standards. It was unclear which to hold the company to.
Wait, what? What happened to all the bloviating earlier about the lack of consent? Now the problem is it ‘crosses boundaries’? WTF. Also: still nothing about how this was ‘bad science’.
If you were a researcher at Facebook, probably one of the things that would provide you with the greatest source of tension about your job would be evidence that the product you’re pushing to half the world’s population actually causes them to feel “negative or left out.” That would be a pretty epic fail for a company that wants to “make the world more open and connected.”
I believe that Kramer is concerned with addressing the popular worry that Facebook makes us unhappy. Not just because I’ve met him but because, in the study, he seems adamant about refuting it. In discussing his findings, Kramer asserts that the study “stands in contrast to theories that suggest viewing positive posts by friends on Facebook may somehow affect us negatively, for example, via social comparison.”
…[long description of ‘social comparison’ which I’m not sure why is in there since the experiment in question strongly suggests it’s not relevant]
Yes, it would suck if that were true and would undermine Facebook’s value, so kudos to Facebook for not hiding its head under a rock and experimenting to find out the truth. Kudos… wait, I forgot, this is ‘lousy social science’ we’re supposed to be booing and hissing about.
In fact, social comparison is often posited as the solution to what’s known as the “Easterlin Paradox,” which finds that, while our happiness increases with our income, societies that get richer do not tend to get happier.
Actually, if you look at the graphs, they do tend to get happier it’s just there’s severe diminishing returns and the graph looks logarithmic rather than linear. Minor point, but it annoys me to think that being wealthier doesn’t help. It does.
[another 5 screens of meandering somewhat related speculation]
In fact, she finds that greater passive consumption over time, controlling for individual predispositions, is associated with lower perceived social support, lower bridging social capital (feeling part of a broader community), and marginally lower positive affect, higher depression, and higher stress.
Gee, I wonder why that might be… No, let’s jump to the insinuation that Facebook causes the higher depression etc. Yeah, that’s plausible.
The first question about the study is whether anything notable happened. This was a common criticism. Although Facebook has tremendous scale, it doesn’t mean the scientific community should care about every effect the company can demonstrate. Neither should the company itself work on small stuff that barely moves the needle. Though Kramer said he removed a lot of emotion from users’ News Feeds (between 10–90% of positive or negative posts), he saw very little change in the emotions users subsequently expressed. All of the changes were 0.1% or less. That’s not 10% or 1% — that’s 0.1%….Still, the small effects raise important questions. Why were they so small?
Bzzt. First hard scientific criticism, and they failed. The reason the effects were small were, as the paper explicitly discusses (OP did read the paper, right? The whole thing? Not just blogs and media coverage?), the intervention was designed to be small (that’s real ethics for you, not bullshit about informed consent), the intervention only affects one of several news sources each user is exposed to (decreasing the intervention still more), and the measure of mood in subsequent items is itself a very noisy measure (measurement error biases the effect downwards). The results are exactly as one would expect and this is an invalid experiment. http://psychcentral.com/blog/archives/201411ya/06/23/emotional-contagion-on-facebook-more-like-bad-research-methods/ makes the same mistake. The description of how much was removed is also wrong; here’s a quote from the paper:
Two parallel experiments were conducted for positive and negative emotion: One in which exposure to friends’ positive emotional content in their News Feed was reduced, and one in which exposure to negative emotional content in their News Feed was reduced. In these conditions, when a person loaded their News Feed, posts that contained emotional content of the relevant emotional valence, each emotional post had between a 10% and 90% chance (based on their User ID) of being omitted from their News Feed for that specific viewing. It is important to note that this content was always available by viewing a friend’s content directly by going to that friend’s “wall” or “timeline,” rather than via the News Feed. Further, the omitted content may have appeared on prior or subsequent views of the News Feed. Finally, the experiment did not affect any direct messages sent from one user to another…Both experiments had a control condition, in which a similar proportion of posts in their News Feed were omitted entirely at random (ie. without respect to emotional content). Separate control conditions were necessary as 22.4% of posts contained negative words, whereas 46.8% of posts contained positive words. So for a person for whom 10% of posts containing positive content were omitted, an appropriate control would withhold 10% of 46.8% (ie. 4.68%) of posts at random, compared with omitting only 2.24% of the News Feed in the negativity-reduced control.
Note the difference between writholding ‘4.68% of posts’ or ‘2.24% of the News Feed’ and OP’s desccription as removing ‘between 10-90% of positive or negative posts’.
Words were determined to be positive or negative using a dictionary provided by the Linguistic Inquiry and Word Count software, known as LIWC, last updated in 200718ya. About 47% of posts in the experiment contained positive words while about 22% of posts contained negative words, leaving 31% of posts with no emotional words at all, as defined by LIWC. Everything but the text of the posts was discarded for this analysis, including photos.
The third study, which looks at the contagion of negative emotion in instant messaging, finds that LIWC actually cannot tell the difference between groups sharing negative versus neutral emotions.
Protip: don’t cite broken links like http://dbonline.igroupnet.com/ACM.TOOLS/Rawdata/Acm1106/fulltext/1980000/1979049/p745-guillory.pdf without any other citation data. I can’t figure out what this study is supposed to be but given that the link is broken despite the blog post being written barely a month or two ago, I suspect OP is misrepresenting it.
Looking more broadly, one study compares a number of similar techniques and finds that LIWC is a middling performer, at best. It is consistently too positive in its ratings, even labeling the conversation in social media around the H1N1 disease outbreak as positive overall. Another study that looks at emotional contagion in instant messaging finds that, even when participants have been induced to feel sad, LIWC still thinks they’re positive.
Good thing the experiment tested multiple conditions and found similar results.
Used in raw form as in the Facebook experiment, however, it appears to be substantially inferior to machine learning.
Sure. But should we let the perfect be the enemy of better?
Further, we know next to nothing about how well LIWC performs in social media when it comes to emotions under the big headings of positive and negative emotion. If it detects some negative emotions, like anger, better than others like sadness this too may bias what we learn from the Facebook experiment.
Yes, maybe the LIWC works well in these circumstances, maybe it doesn’t. Who knows? One could write this of any instrument or analysis being applied in a new situation. I hear the philosophers call this ‘the problem of induction’; maybe they have a solution.
In a word: no. Facebook posts are likely to be a highly biased representation of how Facebook makes people feel because Facebook posts are a highly biased representation of how we feel in general…Looking at social situations in general, we know for example that there are powerful pressures to conform to the attitudes, feelings and beliefs of others. And so if we look at Facebook from this standpoint, it’s easy to see how the effects reported in the Facebook experiment might be due to conformity rather than genuine emotional contagion. Consciously or unconsciously, we may sense a certain emotional tone to our News Feeds and therefore adapt what we post, ever so slightly, so that we don’t stick out too much.
Oh for heaven’s sake. So if they had found a ‘social comparison’ effect, then that’s proof of social comparison; and if they didn’t, well, that’s OK because ‘Facebook posts are likely to be highly biased’ and it’s all due to conformity! Way to explain every possible outcome there, OP. Just being biased doesn’t mean you can’t randomize interventions and learn.
Experience sampling involves randomly interrupting people as they go about their lives to ask how they’re feeling in the moment. It’s private, so it’s less subject to social biases. It does not rely on recollections, which can be off. And it solicits experiences evenly across time, rather than relying on only the moments or feelings people think to share.
But wait! I thought we ‘consciously or unconsciously’ self-censored, and “If we censor fully a third of what we want to express at the last minute, how much are we censoring before we even reach for the keyboard? [to report an experience sample]”? So the question is which source of bias do we prefer: people knowing they’re in an experiment and responding to perceived experimenter demands, or people not knowing and going about life as normal? I know which I prefer, especially since the research has actually been done…
…
Oh my god, it just keeps going on and on doesn’t it? Dude really likes experience sampling, but I’m thinking he needs to write more concisely. OK, I’m going to wrap up here because I’d like to read something else today. Let’s summarize his complaints and my counter-objections:
no consent: irrelevant to whether this was good science or ‘lousy social science’
crossed boundaries between corporations and academia: likewise irrelevant; also, welcome to the modern Internet
small effect size: misunderstood the statistical design of study and why it was designed & expected to have small effects
used LIWC with high error rate for measuring emotionality of posts: if random error, biases effect to zero and so is not an argument against statistically-significant findings
and LIWC may have systematic error towards positivity: apparently not an issue as negative & positive conditions agreed, and the studies he cites in support of this claim are mixed or unavailable
also, other methods are better than LIWC: sure. But that doesn’t mean the results are wrong
maybe LIWC has large unknown biases applied to short social media texts: possible, but it’s not like you have any real evidence for that claim
Facebook news posts are a biased source of mood anyway: maybe, but they still changed after random manipulation
experience sampling is sooooooo awesome: and also brings up its own issues of biases and I don’t see how this would render the Facebook study useless anyway even if we granted it (like complaints #1, 2, 6, 7)
Now, I don’t want to overstate my criticisms here. The author has failed to show the Facebook study is worthless (I’d wager much more money on the Facebook results replicating than 95% of the social science research I’ve read) and it would be outright harmful for Facebook to aim for large effect sizes in future studies, but he does at least raise some good points about improving the followup work: Facebook certainly should be providing some of its cutting-edge deep networks for sentiment analysis for research like this after validating them if it wants to get more reliable results, and it would be worthwhile to run experience sampling approaches to see what happens there, in addition to easier website tests (in addition, not instead of).
Correlation=Causation in Cancer Research
Failed attempt at estimating P(causation|correlation):
How often does correlation=causality? While I’m at it, here’s an example of how not to do it… “A weight of evidence approach to causal inference”, Swaen & van 2009:
Objective: The Bradford Hill criteria are the best available criteria for causal inference. However, there is no information on how the criteria should be weighed and they cannot be combined into one probability estimate for causality. Our objective is to provide an empirical basis for weighing the Bradford Hill criteria and to develop a transparent method to estimate the probability for causality. Study Design and Setting: All 159 agents classified by International Agency for Research of Cancer as category 1 or 2A carcinogens were evaluated by applying the nine Bradford Hill criteria. Discriminant analysis was used to estimate the weights for each of the nine Bradford Hill criteria.
Results: The discriminant analysis yielded weights for the nine causality criteria. These weights were used to combine the nine criteria into one overall assessment of the probability that an association is causal. The criteria strength, consistency of the association and experimental evidence were the three criteria with the largest impact. The model correctly predicted 130 of the 159 (81.8%) agents. Conclusion: The proposed approach enables using the Bradford Hill criteria in a quantitative manner resulting in a probability estimate of the probability that an association is causal.
Sounds reasonable, right? Take this IARC database, presumably of carcinogens known to be such by randomized experiment, and see how well the correlate studies predict after training with LDA - you might not want to build a regular linear model because those tend to be weak and not too great at prediction rather than inference. It’s not clear what they did to prevent overfitting, but reading through, something else strikes me:
The IARC has evaluated the carcinogenicity of a substantial number of chemicals, mixtures, and exposure circumstances. These evaluations have been carried out by expert interdisciplinary panels of scientists and have resulted in classification of these agents or exposure conditions into human carcinogens (category 1) probable human carcinogens (category 2A), possible human carcinogens (category 2B), not classifiable agents (category 3), and chemicals that are probably not carcinogenic to humans (category 4) (IARC, 200619ya). Although the IARC Working Groups do not formally use the Bradford Hill criteria to draw causal inferences many of the criteria are mentioned in the individual reports. For instance, the preamble specifically mentions that the presence of a dose-eresponse is an important consideration for causal inference. In this analysis, the IARC database serves as the reference database although we recognize that it may contain some disputable classifications. However, to our knowledge there is no other database containing causal inferences that were compiled by such a systematic process involving leading experts in the areas of toxicology and epidemiology.
Wait.
These evaluations have been carried out by expert interdisciplinary panels of scientists and have resulted in classification of these agents or exposure conditions into human carcinogens
evaluations have been carried out by expert interdisciplinary panels
IARC Working Groups do not formally use the Bradford Hill criteria to draw causal inferences many of the criteria are mentioned
Wait. So their database with causality/non-causality classifications is… based on… opinion. They got some experts together and asked them.
And the experts use the same criterion which they are using to predict the classifications.
What. So it’s circular. Worse than circular, randomization and causality never even enter the picture. They’re not doing ‘causal inference’, nor are they giving an ‘overall assessment of the probability that an association is causal’. And their conclusion (“The proposed approach enables using the Bradford Hill criteria in a quantitative manner resulting in a probability estimate of the probability that an association is causal.”) certainly is not correct - at best, they are predicting expert opinion (and maybe not even that well), they have no idea how well they’re predicting causality.
But wait, maybe the authors aren’t cretins or con artists, and have a good justification for this approach, so let’s check out the Discussion section where they discuss RCTs:
Using the results from randomized controlled clinical trials as the gold standard instead of the IARC database could have been an alternative approach for our analysis. However, this alternative approach has several disadvantages. First, only a selection of risk factors reported in the literature have been investigated by means of trials, certainly not the occupational and environmental chemicals. Second, there are instances in which randomized trials have yielded contradictory results, for instance, in case of several vitamin supplements and cancer outcomes.
You see, randomized trials are bad because sometimes we haven’t done them but we still really really want to make causal inferences so we’ll just pretend we can do that; and sometimes they disagree with each other and contradict what we epidemiologists have already proven, while the experts & IARC database never disagrees with themselves! Thank goodness we have official IARC doctrine to guide us in our confusion…
This must be one of the most brazen “it’s not a bug, it’s a feature!” moves I’ve ever seen. Mon chapeau, Gerard, Ludovic; mon chapeau.
Incidentally, Google Scholar says this paper has been cited at least 40 times; looking at some, it seem the citations are generally all positive. These are the sort of people deciding what’s a healthy diet and what substances are dangerous and what should be permitted or banned.
Enjoy your dinners.
Aerobic vs Weightlifting
Aerobic vs weightlifting exercise claims: multiple problems but primarily p-hacking, difference-in-statistical-significance-is-not-a-significant-difference, and controlling for intermediate variable.
…For example, weightlifting enhances brain function, reverses sarcopenia, and lowers the death rate in cancer survivors. Take this last item, lowering death rate in cancer survivors: garden-variety aerobic exercise had no effect on survival, while resistance training lowered death rates by one third… –http://roguehealthandfitness.com/case-for-weightlifting-as-anti-aging/
[paper in question: “The Effect of Resistance Exercise on All-Cause Mortality in Cancer Survivors”, et al 2014; https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4126241/ ]
This is a bad study, but sadly the problems are common to the field. Claiming that this study shows ‘weight lifting lowered death rates and aerobic exercise did not change survival’ is making at least 4 errors:
correlation!=causation; this is simply your usual correlation study (you know, of the sort which is always wrong in diet studies?), where you look at some health records and crank out some p-values. There should be no expectation that this will prove to be causally valid; in particular, reverse confounding is pretty obvious here and should remind people of the debate about weight and mortality. (Ah, but you say that the difference they found between aerobic and resistance shows that it’s not confounding because health bias should operate equally? Well, read on…)
power: with only 121 total deaths (~4% of the sample), this is inadequate to detect any differences but comically large correlates of health, as the estimate of predicting a third less mortality indicates
p-hacking/multiplicity, type S errors, exaggeration factor: take a look at that 95% confidence interval for resistance exercise (which is the only result they report in the abstract), which is an HR of 0.45-0.99. In other words, if the correlate were even the tiniest bit bigger, it would no longer have the magical ‘statistical-significance at p<0.05’. There’s at least 16 covariates, 2 stratifications, and 3 full models tested (that they report). By the statistical-significance filter, a HR of 0.67 will be a serious exaggeration (because only exaggerated estimates would - just barely - reach p=0.05 on this small dataset with only 121 deaths). We can rule out a HR of 0.67 as credible simply on a priori grounds: no exercise RCT has ever shown reductions in all-cause mortality remotely like that, and that’s the sort of reduction you just don’t see outside of miracle drugs for lethal diseases (for example, aspirin and vitamin D have RRs of >0.95).
“The Difference Between ‘Significant’ and ‘Not Significant’ is Not Itself Statistically-Significant” (http://www.stat.columbia.edu/~gelman/research/published/signif4.pdf): the difference between aerobic exercise and resistance exercise is not statistically-significant in this study. The HR in model 1 for aerobic exercise is (0.63-1.32), and for aerobic exercise, (0.46-0.99). That is, the confidence intervals overlap. (Specifically, comparing the proportion of aerobic exercisers who died with the resistance exercisers who died, I get
prop.test(c(39,75), c(1251,1746))= p=0.12; to compute a survival curve I would need more data, I think.) The study itself does not anywhere seem to directly compare aerobic with resistance but always works in a stratified setting; I don’t know if they don’t realize this point about the null hypotheses they’re testing, or if they did do the logrank test and it came out non-statistically-significant and they quietly dropped it from the paper.the fallacy of controlling for intermediate variables: in the models they fit, they include as covariates “body mass index, current smoking (yes or no), heavy drinking (yes or no), hypertension (present or not), diabetes (present or not), hypercholesterolemia (yes or no), and parental history of cancer (yes or no).” This makes no sense. Both resistance exercise and aerobic exercise will themselves influence BMI, smoking status, hypertension, diabetes, and hypercholesterolemia. What does it mean to estimate the correlation of exercise with health which excludes all impact it has on your health through BMI, blood pressure, etc? You might as well say, ‘controlling for muscle percentage and body fat, we find weight lifting has no estimated benefits’, or ‘controlling for education, we find no benefits to IQ’ or ‘controlling for local infection rates, we find no mortality benefits to public vaccination’. This makes the results particularly nonsensical for the aerobic estimates if you want to interpret them as direct causal estimates - at most, the HR estimates here are an estimate of weird indirect effects (‘the remaining effect of exercise after removing all effects mediated by the covariates’). Unfortunately, structural equation models and Bayesian networks are a lot harder to use and justify than just dumping a list of covariates into your survival analysis package, so expect to see a lot more controlling for intermediate variables in the future.
The first three are sufficient to show you should not draw any strong conclusions, the latter two are nasty and could be problematic but can be avoided. These concerns are roughly ranked by importance: #1 puts a low ceiling on how much confidence in causality we could ever derive, a ceiling I informally put at ~33%; #2 is important because it shows that very little of the sampling error has been overcoming; #3 means we know the estimate is exaggerated; #4 is not important, because while that misinterpretation is tempting and the authors do nothing to stop the reader from making it, there’s still enough data in the paper that you can correct for it easily by doing your own proportion test; #5 could be an important criticism if anyone was relying heavily on the estimate contaminated by the covariates but in this case the raw proportions of deaths is what yields the headlines, so I bring this up to explain why we should ignore model 3’s estimate of aerobic exercise’s RR=1. This sort of problem is why one should put more weight on meta-analyses of RCTs - for example, “Progressive resistance strength training for improving physical function in older adults” https://onlinelibrary.wiley.com/enhanced/doi/10.1002/14651858.CD002759.pub2
So to summarize: this study collected the wrong kind of data for comparing mortality reduction from aerobics vs weightlifting, insufficient mortality data to result in strong evidence, exaggerates the result through p-hacking, did not actually compare aerobics and weightlifting head to head, and the analysis’s implicit assumptions would ignore much of any causal effects of aerobics/weightlifting!
Moxibustion Mouse Study
http://www.eurekalert.org/pub_releases/2013-12/nrr-pam120513.php … “Pre-moxibustion and moxibustion prevent Alzheimer’s disease” … http://www.sjzsyj.org/CN/article/downloadArticleFile.do?attachType=PDF&id=754
I don’t believe this for a second. But actually, this would be a nice followup to my previous email about the problems in animal research: this paper exhibits all the problems mentioned, and more. Let’s do a little critique here.
This paper is Chinese research performed in China by an all-Chinese team. The current state of Chinese research is bad. It’s really bad. Some reading on the topic:
https://web.archive.org/web/20131203150612/https://www.wired.co.uk/news/archive/2013-12/02/china-academic-scandal
https://newhumanist.org.uk/2365/lies-damn-lies-and-chinese-science
https://news.bbc.co.uk/2/hi/8448731.stm
https://gwern.net/doc/statistics/bias/2010-zhang.pdf
https://www.nytimes.com/201015ya/10/07/world/asia/07fraud.html
https://news.bbc.co.uk/1/hi/world/asia-pacific/4755861.stm
https://news.bbc.co.uk/2/hi/asia-pacific/8442147.stm
https://www.nature.com/articles/463142a
https://www.sciencenews.org/view/generic/id/330930/title/Traditional_Chinese_medicine_Big_questions
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0020185
https://www.npr.org/201114ya/08/03/138937778/plagiarism-plague-hinders-chinas-scientific-ambition
I will note that there have been statistical anomalies in some of the Chinese papers on dual n-back training I have used in my meta-analysis, so I have some personal experience in the topic. #. ‘traditional medicine’ research is really bad no matter where you go. They mention acupuncture as justification? That’s just fantastic. https://en.wikipedia.org/wiki/Acupuncture punctures some of the hyperbolic claims, the PLOS link above deals with the poor-quality of the Chinese reviews & meta-analyses in general, and Cochrane is not too kind to acupuncture: https://www.thecochranelibrary.com/details/collection/691705/Acupuncture-ancient-tradition-meets-modern-science.html And in many of the reviews/meta-analyses there are stark geographic differences where the East Asian studies turn in tons of positive results while the Western studies somehow… don’t. #. The lead author is not an ordinary neuroscientist or doctor, but works at the “College of Acupuncture and Moxibustion”. Is he really going to publish a study concluding “moxibustion does not affect Alzheimer’s”⸮ Really⸮ #. Does this claim even make sense? Moxibustion, really⸮ For those not familiar, https://en.wikipedia.org/wiki/Moxibustion entails
> Suppliers usually age the mugwort and grind it up to a fluff;practitioners burn the fluff or process it further into a cigar-shaped stick. They can use it indirectly, with acupuncture needles, or burn it on the patient’s skin.
How on earth is this supposed to help AD? How does burning a planton your skin affect plaques in your brain? Or if they use acupuncture needles, how plausible is it that a few milligrams at most of mugwort inserted into the skin would do anything? While Wikipedia is not Cochrane or anything, it is troubling that this entry lists no useful application of moxibustion. And then it goes and links to “Does moxibustion work? An overview of systematic reviews” https://www.biomedcentral.com/1756-0500/3/284 which finds that
> Ten SRs met our inclusion criteria, which related to thefollowing conditions: cancer, ulcerative colitis, stroke rehabilitation, constipation, hypertension, pain conditions and breech presentation. Their conclusions were contradictory in several instances. Relatively clear evidence emerged to suggest that moxibustion is effective for breech presentation.
That review also mentions, incidentally, that
> Many of the primary moxibustion trials originate from China(data not shown); Vickers et al. demonstrated that virtually 100% of Chinese acupuncture trials are positive [ /doc/statistics/bias/1998-vickers.pdf], which seems to be equally applied to moxibustion, an acupuncture-like intervention. This casts considerable doubt on the reliability of these studies.
Alright, so let’s take stock here. Without ever looking beyond the title and authorship, we have found that this is a paper from a country with infamously bad research, in a field with infamously bad research quality, led by a researcher with considerable inherent conflict of interest, using a technique/substance which has already been linked with biased research, on a hypothesis that is grossly implausible. Based on all these base rates, we can say that there is basically zero chance this result will ever replicate, much less to other mice strains or even to humans.
It seems unfair to reject the paper out of hand, though, so let’s look at the actual paper a little.
Forty healthy rats were randomly divided into four groups: control group, model group, moxibustion group and pre-moxibustion group. The latter three groups were treated with intracerebral injection of Aβ1–42 to establish an AD-like pathology. The moxibustion group received suspended moxibustion on Baihui and Shenshu acupoints for 14 days after Aβ1–42 injection. The pre-moxibustion group was treated with moxibustion for eight courses (each course lasting for 6 days) prior to the exposure and 14 days after Aβ1–42 exposure. The final analysis incorporated all rats.
From the materials and methods:
Male Wistar rats (12 months old; 500 ± 20 g), of specific pathogen free grade, were obtained from the Experimental Animal Center of Huazhong University of Science and Technology (Wuhan, China), with license No. SCXK (E) 2008-0005.
After the hair around the acupoints was shaved, an ignited moxa-stick (diameter 6 mm; Nanyang Shennong Aaicao Appliance Company, Nanyang, Henan China; a round long stick made of moxa floss, also called moxa roll), was suspended perpendicularly 2 cm above the acupoints. Baihui (located in the middle of the parietal bone[50]) and Shenshu (located under the second lumbar on both sides [50]) acupoints were simultaneously given suspended moxibustion. Each treatment consisted of a 15-minute moxibustion, keeping the spot warm and red but not burnt. Generally, the skin temperature was kept at 43 ± 1° during the moxibustion procedure.
Right away we can spot 3 of the usual animal research methodological problems:
the sample size is too small - at n=10 rats in each group, you are not going to detect anything without large effect sizes. It is implausible that suspended moxa has any effects, and it is especially implausible that the effect sizes would be large.
there is no mention of blinding. The technicians or research assistants or whomever clearly know which mice they are dealing with.
there is mention of randomization, but it’s not specified how the randomization was done, which means it probably was done by the ‘stick your hand in and grab’ method, and probably does not balance by litter or other variables. This massively worsens the power problem, see “Design, power, and interpretation of studies in the standard murine model of ALS” http://www.researchals.org/uploaded_files/ALS%202008%209%204.pdf
(I’m a little curious about whether they really started with 10 mice in each group: the mice spent at least 60 days in the experiment and I wonder how many, out of 40, you would expect to die in that time period, especially after you’ve done your level best to give 3⁄4s of them Alzheimer’s disease during that time.)
I also note that the moxibustion situation is even worse than I thought: they did not use acupuncture needles to get some mugwort into the mice, they did not put any moxa/mugwort in physical contact, but instead the burning was 2cm away from the mice! The mechanism was bad, but it just got worse.
There’s no mention of the data being provided anywhere at all, either their website or the publisher; there’s some evidence that providing access to a paper’s data correlates with higher-quality research, so I mention this absence. It also makes it harder for me to do anything more complex like a post hoc power analysis.
Moving on, they list as dependent variables:
Morris water maze navigation test
Morris water maze spatial probe test
apoptosis rate of hippocampal neurons
Let’s look at the stats a bit.
Significance: The paper lists no less* than 14 p-values (4 < 0.05, the rest < 0.01), and for all of them uses an alpha of 0.05. The smallest given constraint is p<0.01. A Bonferroni correction on this would be 0.05/14 (since they must have done at least 14 tests to report 14 p-values), which means an alpha of 0.003571. But 0.01 > 0.05/14, so the 4 0.05 p-values disappear under multiple correction and probably most of the 0.01s would too.
this is a lower bound since the Morris diagrams report something like 20 p-values themselves, but I didn’t feel like carefully parsing the text to figure out exactly how many p-values are being reported
Effect sizes: no tables are provided, but figure 2 (the second Morris maze test) is illustrative. The control mice have no problem remember where the platform used to be, and so spend almost half a minute (~24s) in the right area searching for it. Makes sense, they don’t have AD. The AD mice have terrible memory, and so only spend ~6s in the right area and most of their time in the wrong place. Also makes sense. Now, what about the AD mice who had some moxa burnt 2cm away from their skin? They spend 14-16s or more than twice and almost 3 times as much as the non-moxa AD mice! And the claimed standard error on all 4 group of mice’s time is tiny, maybe 1s eyeballing the graph. So they are claiming, in this point, to have an effect size on memory of something like d = (15-6)/1 = 9. Insane! From burning some mugwort 2cm away from the mice’s skin‽
Power: actually, that result shows an example of what I mean by the result being absurd. Let’s calculate what that effect size implies for the power of their t-test comparing the model AD mice with the moxa AD mice. So let’s say the 2 moxa groups equate to n=20 15(1.5), and the AD controls were then n=10 5(0.5). The pooled standard deviation of the non-moxa and moxa mice is sqrt(((20-1)(1.5^2) + (10-1)(0.5^2)) / (20 + 10 - 2)) = 1.267, so the effect size was actually d=(15-5)/1.267 = 7.89. With 20 mice in 1 group and 10 mice in the other, an alpha of 0.05, then our power turns out to be…
library(pwr) pwr.t2n.test(n1 = 20, n2 = 10, d = 7.89, sig.level = 0.05) t test power calculation n1 = 20 n2 = 10 d = 7.89 sig.level = 0.05 power = 1
A power of 100%. Absurd. Have you ever seen animal research (or Alzheimer’s research…) with such high power? Real effects, real treatments, in large clinical trials or in meta-analyses, are hardly ever that high.
So. I don’t know how they got the results they got. Did they administer dozens of tests until they got the results they wanted? Did they simply make up the data like so many Chinese academics have? Or did they start with 30 mice in each group and cherrypick the best/worst 10? Did they abuse the model AD mice to make the AD+moxa mice look good?
In conclusion: this paper is complete bullshit, will not replicate.
“Someone Should Do Something”: Wishlist of Miscellaneous Project Ideas
Split out to list of ideas.
Estimating Censored Test Scores
An acquaintance asks the following question: he is applying for an university course which requires a certain minimum score on a test for admittance, and wonders about his chances and a possible trend of increasing minimum scores over time. (He hasn’t received his test results yet.) The university doesn’t provide a distribution of admittee scores, but it does provide the minimum scores for 2005–8201312ya, unless all applicants were admitted because they all scored above an unknown cutoff—in which case it provides no minimum score. This leads to the dataset:
2005,NA
2006,410
2007,NA
2008,NA
2009,398
2010,407
2011,417
2012,NA
2013,NAA quick eyeball tells us that we can’t conclude much: only 4 actual datapoints, with 5 hidden from us. We can’t hope to conclude anything about time trends, other than there doesn’t seem to be much of one: the last score, 417, is not much higher than 410, and the last two scores are low enough to be hidden. We might be able to estimate a mean, though.
We can’t simply average the 4 scores and conclude the mean minimum is 410 because of those NAs: a number of scores have been ‘censored’ because they were too low, and while we don’t know what they were, we do know they were <398 (the smallest score) and so a bunch of <398s will pull down the uncensored mean of 410.
On approach is to treat it as a Tobit model and estimate using something like the censReg library (overview).
But if we try a quick call to censReg, we are confounded: a Tobit model expects you to provide the cutoff below which the observations were censored, but that is something we don’t know. All we know is that it must be below 398, we weren’t told it was exactly 395, 394, etc. Fortunately, this is a solved problem. For example: “The Tobit model with a non-zero threshold”, 2007 tells us:
In this paper, we consider estimating the unknown censoring threshold by the minimum of the uncensored yi’s. We show that the estimator γ’ of γ is superconsistent and asymptotically exponentially distributed. Carson (198837ya, 198936ya) also suggests estimating the unknown censoring threshold by the minimum of the uncensored yi’s. In a recent paper, Zuehlke (200322ya) rediscovers these unpublished results and demonstrates via simulations that the asymptotic distribution of the maximum likelihood estimator does not seem to be affected by the estimation of the censoring threshold.
That seems to be almost too simple and easy, but it makes sense and reminds me a little of the German tank problem: the minimum might not be that accurate a guess (it’s unlikely you just happened to draw a sample right on the censoring threshold) and it definitely can’t be wrong in the sense of being too low. (A Bayesian method might be able to do better with a prior like an exponential.)
With that settled, the analysis is straightforward: load the data, figure out the minimum score, set the NAs to 0, regress, and extract the model estimates for each year:
scores <- data.frame(Year=2005:2013,
MinimumScore=c(NA,410,NA,NA,398,407,417,NA,NA));
censorThreshold <- min(scores$MinimumScore, na.rm=T)
scores[is.na(scores)] <- 0
library(censReg)
## 'censorThreshold-1' because censReg seems to treat threshold as < and not <=
summary(censReg(MinimumScore ~ Year, left=censorThreshold-1, data=scores))
# Warning message:
# In censReg(MinimumScore ~ Year, left = censorThreshold - 1, data = scores) :
# at least one value of the endogenous variable is smaller than the left limit
#
# Call:
# censReg(formula = MinimumScore ~ Year, left = censorThreshold -
# 1, data = scores)
#
# Observations:
# Total Left-censored Uncensored Right-censored
# 9 5 4 0
#
# Coefficients:
# Estimate Std. error t value Pr(> t)
# (Intercept) -139.9711 Inf 0 1
# Year 0.2666 Inf 0 1
# logSigma 2.6020 Inf 0 1
#
# Newton-Raphson maximisation, 37 iterations
# Return code 1: gradient close to zero
# Log-likelihood: -19.35 on 3 Df
-139.9711 + (0.2666 * scores$Year)
# [1] 394.6 394.8 395.1 395.4 395.6 395.9 396.2 396.4 396.7With so little data the results aren’t very reliable, but there is one observation we can make.
The fact that half the dataset is censored tells us that the uncensored mean may be a huge overestimate (since we’re only looking at the ‘top half’ of the underlying data), and indeed it is. The original mean of the uncensored scores was 410; however, the estimate including the censored data is much lower, 397 (13 less)!
This demonstrates the danger of ignoring systematic biases in your data.
So, trying to calculate a mean or time effect is not helpful. What might be better is to instead exploit the censoring directly: if the censoring happened because everyone got in, then if you showed up in a censored year, you have 100% chance of getting in; while in a non-censored year you have an unknown but <100% chance of getting in; so the probability of a censored year sets a lower bound on one’s chances, and this is easy to calculate as a simple binomial problem—5 out of 9 years were censored years, so:
binom.test(c(5,4))
#
# Exact binomial test
#
# data: c(5, 4)
# number of successes = 5, number of trials = 9, p-value = 1
# alternative hypothesis: true probability of success is not equal to 0.5
# 95% confidence interval:
# 0.212 0.863
# sample estimates:
# probability of success
# 0.5556So we can tell him that he may have a >55% chance of getting in.
The Traveling Gerontologist Problem
A quick probability exercise: Wikipedia mentions Finland has 566 centenarians as of 201015ya.
That’s few enough you could imagine visiting them all to research them and their longevity, in a sort of traveling salesman problem but with gerontologists instead. Except, because of the exponential increase in mortality, centenarians have high annual mortality rates; it depends on the exact age but you could call it >30% (eg. Finnish 99yos in 2012 had a death toll of 326.54/1000). So you might well try to visit a centenarian and discover they’d died before you got there.
How bad a risk is this? Well, if the risk per year is 30%, then one has a 70% chance of surviving a year. To survive a year, you must survive all 365 days; by the multiplication rule, the risk is x where or 0.7 = x365.25; solving, x = 0.999024.
It takes time to visit a centenarian—it wouldn’t do to be abrupt and see them for only a few minutes, you ought to listen to their stories, and you need to get to a hotel or airport, so let’s assume you visit 1 centenarian per day.
If you visit centenarian A on day 1, and you want to visit centenarian B on day 2, then you can count on a 99.9% chance B is still alive. So far so good. And if you wanted to visit 566 centenarians (let’s imagine you have a regularly-updated master list of centenarians from the Finnish population registry), then you only have to beat the odds 566 times in a row, which is not that hard: 0.999024566 = 0.5754023437943274.
But that’s coldblooded of you to objectify those Finnish centenarians! “Any centenarian will do, I don’t care.” What if you picked the current set of 566 centenarians and wanted to visit just them, specifically—with no new centenarians introduced to the list to replace any dead ones.
That’s a little more complicated. When you visit the first centenarian, it’s the same probability: 0.999024. When you visit the second centenarian the odds change since now she (and it’s more often ‘she’ than ‘he’, since remember the exponential and males having shorter mean lifetimes) has to survive 2 days, so it’s or 0.9990242; for the third, it’s 0.9990243, and so on to #566 who has been patiently waiting and trying to survive a risk of 0.999024566, and then you need to multiply to get your odds of beating every single risk of death and the centenarian not leaving for a more permanent rendezvous: , which would be , or in Haskell:
product (map (\x -> 0.999024**x) [1..566])
→ 8.952743340164081e-69(A little surprisingly, Wolfram Alpha can solve the TeX expression too.)
Given the use of floating point in that function (567 floating point exponentiations followed by as many multiplications) and the horror stories about floating point, one might worry the answer is wrong & the real probability is much larger. We can retry with an implementation of computable reals, CReal, which can be very slow but should give more precise answers:
:module + Data.Number.CReal
showCReal 100 (product (map (\x -> 0.999024**x) [1..566]))
→ 0.0000000000000000000000000000000000000000000000000000000000000000000089527433401308585720915431195262Looks good—agrees with the floating point version up to the 11th digit:
8.9527433401 64081e-69
8.9527433401 308585720915431195262We can also check by rewriting the product equation to avoid all the exponentiation and multiplication (which might cause issues) in favor of a single exponential:
(as before)
= (since )
= (by arithmetic progression/Gauss’s famous classroom trick since )
= (start substituting in specific values)
=
= 0.999024160461
So:
0.999024^160461
→ 8.95274334014924e-69Or to go back to the longer version:
0.999024**((566*(1 + 566)) / 2)
→ 8.952743340164096e-69Also close. All probabilities of success are minute.
How fast would you have to be if you wanted to at least try to accomplish the tour with, say, a 50-50 chance?
Well, that’s easy: you can consider the probability of all of them surviving one day and as we saw earlier, that’s 0.999024566 = 0.58, and two days would be So you can only take a little over a day before you’ve probabilistically lost & one of them has died; if you hit all 566 centenarians in 24 hours, that’s ~24 centenarians per hour or ~2 minutes to chat with each one and travel to the next. If you’re trying to collect DNA samples, better hope they’re all awake and able to give consent!
So safe to say, you will probably not be able to manage the Traveling Gerontologist’s tour.
Bayes Nets
Daily Weight Data Graph
As the datasets I’m interested in grow in number of variables, it becomes harder to justify doing analysis by simply writing down a simple linear model with a single dependent variable and throwing in the independent variables and maybe a few transformations chosen by hand. I can instead write down some simultaneous-equations/structural-equation-models, but while it’s usually obvious what to do for k < 4 and if it’s not I can compare the possible variants, 4 variables is questionable what the right SEM is, and >5, it’s hopeless. Factor analysis to extract some latent variables is a possibility, but the more general solution here seems to be probabilistic graphical models such as Bayesian networks.
I thought I’d try out some Bayes net inference on some of my datasets. In this case, I have ~150 daily measurements from my Omron body composition scale, measuring total weight, body fat percentage, and some other things (see an Omron manual):
Total weight
BMI
Body fat percentage
Muscle percentage
Resting metabolism in calories
“Body age”
Visceral fat index
The 7 variables are interrelated, so this is definitely a case where a simple lm is not going to do the trick. It’s also not 100% clear how to set up a SEM; some definitions are obvious (the much-criticized BMI is going to be determined solely by total weight, muscle and fat percentage might be inversely related) but others are not (how does “visceral fat” relate to body fat?). And it’s not a hopelessly small amount of data.
The Bayes net R library I’m trying out is bnlearn (paper).
library(bnlearn)
weight <- read.csv("https://gwern.net/doc/nootropic/quantified-self/2015-03-22-gwern-weight.csv")
weight$Date <- NULL; weight$Weight.scale <- NULL
# remove missing data
weightC <- na.omit(weight)
# bnlearn can't handle integers, oddly enough
weightC <- as.data.frame(sapply(weightC, as.numeric))
summary(weightC)
# Weight.Omron Weight.BMI Weight.body.fat Weight.muscle
# Min. :193.0000 Min. : 26.90000 Min. :27.00000 Min. :32.60000
# 1st Qu.:195.2000 1st Qu.: 27.20000 1st Qu.:28.40000 1st Qu.:34.20000
# Median :196.4000 Median : 27.40000 Median :28.70000 Median :34.50000
# Mean :196.4931 Mean : 28.95409 Mean :28.70314 Mean :34.47296
# 3rd Qu.:197.8000 3rd Qu.: 27.60000 3rd Qu.:29.10000 3rd Qu.:34.70000
# Max. :200.6000 Max. : 28.00000 Max. :31.70000 Max. :35.50000
# Weight.resting.metabolism Weight.body.age Weight.visceral.fat
# Min. :1857.000 Min. :52.00000 Min. : 9.000000
# 1st Qu.:1877.000 1st Qu.:53.00000 1st Qu.:10.000000
# Median :1885.000 Median :53.00000 Median :10.000000
# Mean :1885.138 Mean :53.32704 Mean : 9.949686
# 3rd Qu.:1893.000 3rd Qu.:54.00000 3rd Qu.:10.000000
# Max. :1914.000 Max. :56.00000 Max. :11.000000
cor(weightC)
# Weight.Omron Weight.BMI Weight.body.fat Weight.muscle
# Weight.Omron 1.00000000000 0.98858376919 0.1610643221 -0.06976934825
# Weight.BMI 0.98858376919 1.00000000000 0.1521872557 -0.06231142104
# Weight.body.fat 0.16106432213 0.15218725566 1.0000000000 -0.98704369855
# Weight.muscle -0.06976934825 -0.06231142104 -0.9870436985 1.00000000000
# Weight.resting.metabolism 0.96693236051 0.95959140245 -0.0665001241 0.15621294274
# Weight.body.age 0.82581939626 0.81286141659 0.5500409365 -0.47408608681
# Weight.visceral.fat 0.41542744168 0.43260100665 0.2798756916 -0.25076619829
# Weight.resting.metabolism Weight.body.age Weight.visceral.fat
# Weight.Omron 0.9669323605 0.8258193963 0.4154274417
# Weight.BMI 0.9595914024 0.8128614166 0.4326010067
# Weight.body.fat -0.0665001241 0.5500409365 0.2798756916
# Weight.muscle 0.1562129427 -0.4740860868 -0.2507661983
# Weight.resting.metabolism 1.0000000000 0.7008354776 0.3557229425
# Weight.body.age 0.7008354776 1.0000000000 0.4840752389
# Weight.visceral.fat 0.3557229425 0.4840752389 1.0000000000
## create alternate dataset expressing the two percentage variables as pounds, since this might fit better
weightC2 <- weightC
weightC2$Weight.body.fat <- weightC2$Weight.Omron * (weightC2$Weight.body.fat / 100)
weightC2$Weight.muscle <- weightC2$Weight.Omron * (weightC2$Weight.muscle / 100)Begin analysis:
pdap <- hc(weightC)
pdapc2 <- hc(weightC2)
## bigger is better:
score(pdap, weightC)
# [1] -224.2563072
score(pdapc2, weightC2)
# [1] -439.7811072
## stick with the original, then
pdap
# Bayesian network learned via Score-based methods
#
# model:
# [Weight.Omron][Weight.body.fat][Weight.BMI|Weight.Omron]
# [Weight.resting.metabolism|Weight.Omron:Weight.body.fat]
# [Weight.body.age|Weight.Omron:Weight.body.fat]
# [Weight.muscle|Weight.body.fat:Weight.resting.metabolism][Weight.visceral.fat|Weight.body.age]
# nodes: 7
# arcs: 8
# undirected arcs: 0
# directed arcs: 8
# average markov blanket size: 2.57
# average neighbourhood size: 2.29
# average branching factor: 1.14
#
# learning algorithm: Hill-Climbing
# score: BIC (Gauss.)
# penalization coefficient: 2.534452101
# tests used in the learning procedure: 69
# optimized: TRUE
plot(pdap)
## https://i.imgur.com/nipmqta.pngThis inferred graph is obviously wrong in several respects, violating prior knowledge about some of the relationships.
More specifically, my prior knowledge:
Weight.Omron== total weight; should be influenced byWeight.body.fat(%),Weight.muscle(%), &Weight.visceral.fatWeight.visceral.fat: ordinal variable, <=9 = normal; 10-14 = high; 15+ = very high; from the Omron manual:Visceral fat area (0—approx. 300 cm , 1 inch=2.54 cm) distribution with 30 levels. NOTE: Visceral fat levels are relative and not absolute values.
Weight.BMI: BMI is a simple function of total weight & height (specificallyBMI = round(weight / height^2)), so it should be influenced only byWeight.Omron, and influence nothing elseWeight.body.age: should be influenced byWeight.Omron,Weight.body.fat, andWeight.muscle, based on the description in the manual:Body age is based on your resting metabolism. Body age is calculated by using your weight, body fat percentage and skeletal muscle percentage to produce a guide to whether your body age is above or below the average for your actual age.
Weight.resting.metabolism: a function of the others, but I’m not sure which exactly; manual talks about what resting metabolism is generically and specifies it has the range “385 to 3999 kcal with 1 kcal increments”; https://en.wikipedia.org/wiki/Basal_metabolic_rate suggests the Omron may be using one of several approximation equations based on age/sex/height/weight, but it might also be using lean body mass as well.
Unfortunately, bnlearn doesn’t seem to support any easy way of encoding the prior knowledge—for example, you can’t say ‘no outgoing arrows from node X’—so I iterate, adding bad arrows to the blacklist.
Which arrows violate prior knowledge?
[Weight.visceral.fat|Weight.body.age](read backwards, asWeight.body.age → Weight.visceral.fat)[Weight.muscle|Weight.resting.metabolism]
Retry, blacklisting those 2 arrows:
pdap2 <- hc(weightC, blacklist=data.frame(from=c("Weight.body.age", "Weight.resting.metabolism"), to=c("Weight.visceral.fat","Weight.muscle")))New violations:
[Weight.visceral.fat|Weight.BMI][Weight.muscle|Weight.Omron]
pdap3 <- hc(weightC, blacklist=data.frame(from=c("Weight.body.age", "Weight.resting.metabolism", "Weight.BMI", "Weight.Omron"), to=c("Weight.visceral.fat","Weight.muscle", "Weight.visceral.fat", "Weight.muscle")))New violations:
[Weight.visceral.fat|Weight.Omron][Weight.muscle|Weight.BMI]
pdap4 <- hc(weightC, blacklist=data.frame(from=c("Weight.body.age", "Weight.resting.metabolism", "Weight.BMI", "Weight.Omron", "Weight.Omron", "Weight.BMI"), to=c("Weight.visceral.fat","Weight.muscle", "Weight.visceral.fat", "Weight.muscle", "Weight.visceral.fat", "Weight.muscle")))One violation:
[Weight.muscle|Weight.body.age]
pdap5 <- hc(weightC, blacklist=data.frame(from=c("Weight.body.age", "Weight.resting.metabolism", "Weight.BMI", "Weight.Omron", "Weight.Omron", "Weight.BMI", "Weight.body.age"), to=c("Weight.visceral.fat","Weight.muscle", "Weight.visceral.fat", "Weight.muscle", "Weight.visceral.fat", "Weight.muscle", "Weight.muscle")))
# Bayesian network learned via Score-based methods
#
# model:
# [Weight.body.fat][Weight.muscle|Weight.body.fat][Weight.visceral.fat|Weight.body.fat]
# [Weight.Omron|Weight.visceral.fat][Weight.BMI|Weight.Omron]
# [Weight.resting.metabolism|Weight.Omron:Weight.body.fat]
# [Weight.body.age|Weight.Omron:Weight.body.fat]
# nodes: 7
# arcs: 8
# undirected arcs: 0
# directed arcs: 8
# average markov blanket size: 2.57
# average neighbourhood size: 2.29
# average branching factor: 1.14
#
# learning algorithm: Hill-Climbing
# score: BIC (Gauss.)
# penalization coefficient: 2.534452101
# tests used in the learning procedure: 62
# optimized: TRUE
plot(pdap5)
## https://i.imgur.com/nxCfmYf.png
## implementing all the prior knowledge cost ~30:
score(pdap5, weightC)
# [1] -254.6061724No violations, so let’s use the network and estimate the specific parameters:
fit <- bn.fit(pdap5, weightC); fit
# Bayesian network parameters
#
# Parameters of node Weight.Omron (Gaussian distribution)
#
# Conditional density: Weight.Omron | Weight.visceral.fat
# Coefficients:
# (Intercept) Weight.visceral.fat
# 169.181651376 2.744954128
# Standard deviation of the residuals: 1.486044472
#
# Parameters of node Weight.BMI (Gaussian distribution)
#
# Conditional density: Weight.BMI | Weight.Omron
# Coefficients:
# (Intercept) Weight.Omron
# -0.3115772322 0.1411044216
# Standard deviation of the residuals: 0.03513413381
#
# Parameters of node Weight.body.fat (Gaussian distribution)
#
# Conditional density: Weight.body.fat
# Coefficients:
# (Intercept)
# 28.70314465
# Standard deviation of the residuals: 0.644590085
#
# Parameters of node Weight.muscle (Gaussian distribution)
#
# Conditional density: Weight.muscle | Weight.body.fat
# Coefficients:
# (Intercept) Weight.body.fat
# 52.1003347352 -0.6141270921
# Standard deviation of the residuals: 0.06455478599
#
# Parameters of node Weight.resting.metabolism (Gaussian distribution)
#
# Conditional density: Weight.resting.metabolism | Weight.Omron + Weight.body.fat
# Coefficients:
# (Intercept) Weight.Omron Weight.body.fat
# 666.910582196 6.767607964 -3.886694779
# Standard deviation of the residuals: 1.323176507
#
# Parameters of node Weight.body.age (Gaussian distribution)
#
# Conditional density: Weight.body.age | Weight.Omron + Weight.body.fat
# Coefficients:
# (Intercept) Weight.Omron Weight.body.fat
# -32.2651379176 0.3603672788 0.5150134225
# Standard deviation of the residuals: 0.2914301529
#
# Parameters of node Weight.visceral.fat (Gaussian distribution)
#
# Conditional density: Weight.visceral.fat | Weight.body.fat
# Coefficients:
# (Intercept) Weight.body.fat
# 6.8781100009 0.1070118125
# Standard deviation of the residuals: 0.2373649058
## residuals look fairly good, except for Weight.resting.metabolism, where there are some extreme residuals in what looks a bit like a sigmoid sort of pattern, suggesting nonlinearities in the Omron scale's formula?
bn.fit.qqplot(fit)
## https://i.imgur.com/mSallOv.pngWe can double-check the estimates here by turning the Bayes net model into a SEM and seeing how the estimates compare, and also seeing if the p-values suggest we’ve found a good model:
library(lavaan)
Weight.model1 <- '
Weight.visceral.fat ~ Weight.body.fat
Weight.Omron ~ Weight.visceral.fat
Weight.BMI ~ Weight.Omron
Weight.body.age ~ Weight.Omron + Weight.body.fat
Weight.muscle ~ Weight.body.fat
Weight.resting.metabolism ~ Weight.Omron + Weight.body.fat
'
Weight.fit1 <- sem(model = Weight.model1, data = weightC)
summary(Weight.fit1)
# lavaan (0.5-16) converged normally after 139 iterations
#
# Number of observations 159
#
# Estimator ML
# Minimum Function Test Statistic 71.342
# Degrees of freedom 7
# P-value (Chi-square) 0.000
#
# Parameter estimates:
#
# Information Expected
# Standard Errors Standard
#
# Estimate Std.err Z-value P(>|z|)
# Regressions:
# Weight.visceral.fat ~
# Weight.bdy.ft 0.107 0.029 3.676 0.000
# Weight.Omron ~
# Wght.vscrl.ft 2.745 0.477 5.759 0.000
# Weight.BMI ~
# Weight.Omron 0.141 0.002 82.862 0.000
# Weight.body.age ~
# Weight.Omron 0.357 0.014 25.162 0.000
# Weight.bdy.ft 0.516 0.036 14.387 0.000
# Weight.muscle ~
# Weight.bdy.ft -0.614 0.008 -77.591 0.000
# Weight.resting.metabolism ~
# Weight.Omron 6.730 0.064 104.631 0.000
# Weight.bdy.ft -3.860 0.162 -23.837 0.000
#
# Covariances:
# Weight.BMI ~~
# Weight.body.g -0.000 0.001 -0.116 0.907
# Weight.muscle -0.000 0.000 -0.216 0.829
# Wght.rstng.mt 0.005 0.004 1.453 0.146
# Weight.body.age ~~
# Weight.muscle 0.001 0.001 0.403 0.687
# Wght.rstng.mt -0.021 0.030 -0.700 0.484
# Weight.muscle ~~
# Wght.rstng.mt 0.007 0.007 1.003 0.316
#
# Variances:
# Wght.vscrl.ft 0.056 0.006
# Weight.Omron 2.181 0.245
# Weight.BMI 0.001 0.000
# Weight.body.g 0.083 0.009
# Weight.muscle 0.004 0.000
# Wght.rstng.mt 1.721 0.193Comparing the coefficients by eye, they tend to be quite close (usually within 0.1) and the p-values are all statistically-significant.
The network itself looks right, although some of the edges are surprises: I didn’t know visceral fat was predictable from body fat (I thought they were measuring separate things), and the relative independence of muscle suggests that in any exercise plan I might be better off focusing on the body fat percentage rather than the muscle percentage since the former may be effectively determining the latter.
So what did I learn here?
learning network structure and direction of arrows is hard; even with only 7 variables and n = 159 (accurate clean data), the hill-climbing algorithm will learn at least 7 wrong arcs.
and the derived graphs depend disturbingly heavily on choice of algorithm; I used the
hchill-climbing algorithm (since I’m lazy and didn’t want to specify arrow directions), but when I try out the alternatives likeiambon the same data & blacklist, the found graph looks rather different
Gaussians are, as always, sensitive to outliers: I was surprised the first graph didn’t show BMI connected to anything, so I took a closer look and found I had miscoded a BMI of 28 as 280!
bnlearn, while not as hard to use as I expected, could still use usability improvements: I should not need to coerce integer data into exactly equivalent numeric types just becausebnlearndoesn’t recognize integers; and blacklisting/whitelisting needs to be more powerful—iteratively generating graphs and manually inspecting and manually blacklisting is tedious and does not scalehence, it may make more sense to find a graph using
bnlearnand then convert it into simultaneous-equations and manipulate it using more mature SEM libraries
Zeo Sleep Data
Here I look at my Zeo sleep data; more variables, more complex relations, and more unknown ones, but on the positive side, ~12x more data to work with.
zeo <- read.csv("~/wiki/doc/zeo/gwern-zeodata.csv")
zeo$Sleep.Date <- as.Date(zeo$Sleep.Date, format="%m/%d/%Y")
## convert "05/12/2014 06:45" to "06:45"
zeo$Start.of.Night <- sapply(strsplit(as.character(zeo$Start.of.Night), " "), function(x) { x[2] })
## convert "06:45" to 24300
interval <- function(x) { if (!is.na(x)) { if (grepl(" s",x)) as.integer(sub(" s","",x))
else { y <- unlist(strsplit(x, ":")); as.integer(y[[1]])*60 + as.integer(y[[2]]); }
}
else NA
}
zeo$Start.of.Night <- sapply(zeo$Start.of.Night, interval)
## correct for the switch to new unencrypted firmware in March 2013;
## I don't know why the new firmware subtracts 15 hours
zeo[(zeo$Sleep.Date >= as.Date("2013-03-11")),]$Start.of.Night <- (zeo[(zeo$Sleep.Date >= as.Date("2013-03-11")),]$Start.of.Night + 900) %% (24*60)
## after midnight (24*60=1440), Start.of.Night wraps around to 0, which obscures any trends,
## so we'll map anything before 7AM to time+1440
zeo[zeo$Start.of.Night<420 & !is.na(zeo$Start.of.Night),]$Start.of.Night <- (zeo[zeo$Start.of.Night<420 & !is.na(zeo$Start.of.Night),]$Start.of.Night + (24*60))
zeoSmall <- subset(zeo, select=c(ZQ,Total.Z,Time.to.Z,Time.in.Wake,Time.in.REM,Time.in.Light,Time.in.Deep,Awakenings,Start.of.Night,Morning.Feel))
zeoClean <- na.omit(zeoSmall)
# bnlearn doesn't like the 'integer' class that most of the data-frame is in
zeoClean <- as.data.frame(sapply(zeoClean, as.numeric))Prior knowledge:
Start.of.Nightis temporally first, and cannot be causedTime.to.Zis temporally second, and can be influenced byStart.of.Night(likely a connection between how late I go to bed and how fast I fall asleep) &Time.in.Wake(since if it takes 10 minutes to fall asleep, I must spend ≥10 minutes in wake) but not othersMorning.Feelis temporally last, and cannot cause anythingZQis a synthetic variable invented by Zeo according to an opaque formula, which cannot cause anything but is determined by othersTotal.Zshould be the sum ofTime.in.Light,Time.in.REM, andTime.in.DeepAwakeningsshould have an arrow withTime.in.Wakebut it’s not clear which way it should run
library(bnlearn)
## after a bunch of iteration, blacklisting arrows which violate the prior knowledge
bl <- data.frame(from=c("Morning.Feel", "ZQ", "ZQ", "ZQ", "ZQ", "ZQ", "ZQ", "Time.in.REM", "Time.in.Light", "Time.in.Deep", "Morning.Feel", "Awakenings", "Time.in.Light", "Morning.Feel", "Morning.Feel","Total.Z", "Time.in.Wake", "Time.to.Z", "Total.Z", "Total.Z", "Total.Z"),
to=c("Start.of.Night", "Total.Z", "Time.in.Wake", "Time.in.REM", "Time.in.Deep", "Morning.Feel","Start.of.Night", "Start.of.Night","Start.of.Night","Start.of.Night", "Time.to.Z", "Time.to.Z", "Time.to.Z", "Total.Z", "Time.in.Wake","Time.to.Z","Time.to.Z", "Start.of.Night", "Time.in.Deep", "Time.in.REM", "Time.in.Light"))
zeo.hc <- hc(zeoClean, blacklist=bl)
zeo.iamb <- iamb(zeoClean, blacklist=bl)
## problem: undirected arc: Time.in.Deep/Time.in.REM; since hc inferred [Time.in.Deep|Time.in.REM], I'll copy that for iamb:
zeo.iamb <- set.arc(zeo.iamb, from = "Time.in.REM", to = "Time.in.Deep")
zeo.gs <- gs(zeoClean, blacklist=bl)
## same undirected arc:
zeo.gs <- set.arc(zeo.gs, from = "Time.in.REM", to = "Time.in.Deep")
## Bigger is better:
score(zeo.iamb, data=zeoClean)
# [1] -44776.79185
score(zeo.gs, data=zeoClean)
# [1] -44776.79185
score(zeo.hc, data=zeoClean)
# [1] -44557.6952
## hc scores best, so let's look at it:
zeo.hc
# Bayesian network learned via Score-based methods
#
# model:
# [Start.of.Night][Time.to.Z|Start.of.Night][Time.in.Light|Time.to.Z:Start.of.Night]
# [Time.in.REM|Time.in.Light:Start.of.Night][Time.in.Deep|Time.in.REM:Time.in.Light:Start.of.Night]
# [Total.Z|Time.in.REM:Time.in.Light:Time.in.Deep][Time.in.Wake|Total.Z:Time.to.Z]
# [Awakenings|Time.to.Z:Time.in.Wake:Time.in.REM:Time.in.Light:Start.of.Night]
# [Morning.Feel|Total.Z:Time.to.Z:Time.in.Wake:Time.in.Light:Start.of.Night]
# [ZQ|Total.Z:Time.in.Wake:Time.in.REM:Time.in.Deep:Awakenings]
# nodes: 10
# arcs: 28
# undirected arcs: 0
# directed arcs: 28
# average markov blanket size: 7.40
# average neighbourhood size: 5.60
# average branching factor: 2.80
#
# learning algorithm: Hill-Climbing
# score: BIC (Gauss.)
# penalization coefficient: 3.614556939
# tests used in the learning procedure: 281
# optimized: TRUE
plot(zeo.hc)
## https://i.imgur.com/nD3LXND.png
fit <- bn.fit(zeo.hc, zeoClean); fit
#
# Bayesian network parameters
#
# Parameters of node ZQ (Gaussian distribution)
#
# Conditional density: ZQ | Total.Z + Time.in.Wake + Time.in.REM + Time.in.Deep + Awakenings
# Coefficients:
# (Intercept) Total.Z Time.in.Wake Time.in.REM Time.in.Deep Awakenings
# -0.12468522173 0.14197043518 -0.07103211437 0.07053271816 0.21121000076 -0.56476256303
# Standard deviation of the residuals: 0.3000223604
#
# Parameters of node Total.Z (Gaussian distribution)
#
# Conditional density: Total.Z | Time.in.Wake + Start.of.Night
# Coefficients:
# (Intercept) Time.in.Wake Start.of.Night
# 907.6406157850 -0.4479377278 -0.2680771514
# Standard deviation of the residuals: 68.90853885
#
# Parameters of node Time.to.Z (Gaussian distribution)
#
# Conditional density: Time.to.Z | Start.of.Night
# Coefficients:
# (Intercept) Start.of.Night
# -1.02898431407 0.01568450832
# Standard deviation of the residuals: 13.51606719
#
# Parameters of node Time.in.Wake (Gaussian distribution)
#
# Conditional density: Time.in.Wake | Time.to.Z
# Coefficients:
# (Intercept) Time.to.Z
# 14.7433880499 0.3289378711
# Standard deviation of the residuals: 19.0906685
#
# Parameters of node Time.in.REM (Gaussian distribution)
#
# Conditional density: Time.in.REM | Total.Z + Start.of.Night
# Coefficients:
# (Intercept) Total.Z Start.of.Night
# -120.62442964234 0.37864195651 0.06275760841
# Standard deviation of the residuals: 19.32560757
#
# Parameters of node Time.in.Light (Gaussian distribution)
#
# Conditional density: Time.in.Light | Total.Z + Time.in.REM + Time.in.Deep
# Coefficients:
# (Intercept) Total.Z Time.in.REM Time.in.Deep
# 0.6424267863 0.9997862624 -1.0000587988 -1.0001805537
# Standard deviation of the residuals: 0.5002896274
#
# Parameters of node Time.in.Deep (Gaussian distribution)
#
# Conditional density: Time.in.Deep | Total.Z + Time.in.REM
# Coefficients:
# (Intercept) Total.Z Time.in.REM
# 15.4961459056 0.1283622577 -0.1187382535
# Standard deviation of the residuals: 11.90756843
#
# Parameters of node Awakenings (Gaussian distribution)
#
# Conditional density: Awakenings | Time.to.Z + Time.in.Wake + Time.in.REM + Time.in.Light + Start.of.Night
# Coefficients:
# (Intercept) Time.to.Z Time.in.Wake Time.in.REM Time.in.Light
# -18.41014329148 0.02605164827 0.05736596152 0.02291139969 0.01060661963
# Start.of.Night
# 0.01129521977
# Standard deviation of the residuals: 2.427868657
#
# Parameters of node Start.of.Night (Gaussian distribution)
#
# Conditional density: Start.of.Night
# Coefficients:
# (Intercept)
# 1413.382886
# Standard deviation of the residuals: 64.43144125
#
# Parameters of node Morning.Feel (Gaussian distribution)
#
# Conditional density: Morning.Feel | Total.Z + Time.to.Z + Time.in.Wake + Time.in.Light + Start.of.Night
# Coefficients:
# (Intercept) Total.Z Time.to.Z Time.in.Wake Time.in.Light
# -0.924662971061 0.004808652252 -0.010127269154 -0.008636841492 -0.002766602019
# Start.of.Night
# 0.001672816480
# Standard deviation of the residuals: 0.7104115719
## some issues with big residuals at the extremes in the variables Time.in.Light, Time.in.Wake, and Time.to.Z;
## not sure how to fix those
bn.fit.qqplot(fit)
# https://i.imgur.com/fmP1ca0.png
library(lavaan)
Zeo.model1 <- '
Time.to.Z ~ Start.of.Night
Time.in.Wake ~ Total.Z + Time.to.Z
Awakenings ~ Time.to.Z + Time.in.Wake + Time.in.REM + Time.in.Light + Start.of.Night
Time.in.Light ~ Time.to.Z + Start.of.Night
Time.in.REM ~ Time.in.Light + Start.of.Night
Time.in.Deep ~ Time.in.REM + Time.in.Light + Start.of.Night
Total.Z ~ Time.in.REM + Time.in.Light + Time.in.Deep
ZQ ~ Total.Z + Time.in.Wake + Time.in.REM + Time.in.Deep + Awakenings
Morning.Feel ~ Total.Z + Time.to.Z + Time.in.Wake + Time.in.Light + Start.of.Night
'
Zeo.fit1 <- sem(model = Zeo.model1, data = zeoClean)
summary(Zeo.fit1)
# lavaan (0.5-16) converged normally after 183 iterations
#
# Number of observations 1379
#
# Estimator ML
# Minimum Function Test Statistic 22.737
# Degrees of freedom 16
# P-value (Chi-square) 0.121
#
# Parameter estimates:
#
# Information Expected
# Standard Errors Standard
#
# Estimate Std.err Z-value P(>|z|)
# Regressions:
# Time.to.Z ~
# Start.of.Nght 0.016 0.006 2.778 0.005
# Time.in.Wake ~
# Total.Z -0.026 0.007 -3.592 0.000
# Time.to.Z 0.314 0.038 8.277 0.000
# Awakenings ~
# Time.to.Z 0.026 0.005 5.233 0.000
# Time.in.Wake 0.057 0.003 16.700 0.000
# Time.in.REM 0.023 0.002 10.107 0.000
# Time.in.Light 0.011 0.002 6.088 0.000
# Start.of.Nght 0.011 0.001 10.635 0.000
# Time.in.Light ~
# Time.to.Z -0.348 0.085 -4.121 0.000
# Start.of.Nght -0.195 0.018 -10.988 0.000
# Time.in.REM ~
# Time.in.Light 0.358 0.018 19.695 0.000
# Start.of.Nght 0.034 0.013 2.725 0.006
# Time.in.Deep ~
# Time.in.REM 0.081 0.012 6.657 0.000
# Time.in.Light 0.034 0.009 3.713 0.000
# Start.of.Nght -0.017 0.006 -3.014 0.003
# Total.Z ~
# Time.in.REM 1.000 0.000 2115.859 0.000
# Time.in.Light 1.000 0.000 2902.045 0.000
# Time.in.Deep 1.000 0.001 967.322 0.000
# ZQ ~
# Total.Z 0.142 0.000 683.980 0.000
# Time.in.Wake -0.071 0.000 -155.121 0.000
# Time.in.REM 0.071 0.000 167.090 0.000
# Time.in.Deep 0.211 0.001 311.454 0.000
# Awakenings -0.565 0.003 -178.407 0.000
# Morning.Feel ~
# Total.Z 0.005 0.001 8.488 0.000
# Time.to.Z -0.010 0.001 -6.948 0.000
# Time.in.Wake -0.009 0.001 -8.592 0.000
# Time.in.Light -0.003 0.001 -2.996 0.003
# Start.of.Nght 0.002 0.000 5.414 0.000Again no major surprises, but one thing I notice is that ZQ does not seem to connect to Time.in.Light, though Time.in.Light does connect to Morning.Feel; I’ve long suspected that ZQ is a flawed summary and thought it was insufficiently taking into account wakes or something else, so it looks like it’s Time.in.Light specifically which is missing. Start.of.night also is more highly connected than I had expected.
Comparing graphs from the 3 algorithms, they don’t seem to differ as badly as the weight ones did. Is this thanks to the much greater data or the constraints?
Genome Sequencing Costs
# https://www.genome.gov/about-genomics/fact-sheets/Sequencing-Human-Genome-cost
# http://www.genome.gov/pages/der/sequencing_costs_apr2014.xls
# converted to CSV & deleted cost per base (less precision)
## Date, Cost per Genome
## Sep-01,"$95,263,072"
## ...
sequencing <- read.csv("sequencing_costs_apr2014.csv")
sequencing$Cost.per.Genome <- as.integer(gsub(",", "", sub("\\$", "", as.character(sequencing$Cost.per.Genome))))
# interpret month-years as first of month:
sequencing$Date <- as.Date(paste0("01-", as.character(sequencing$Date)), format="%d-%b-%y")
head(sequencing)
## Date Cost.per.Genome
## 1 2001-09-01 95263072
## 2 2002-03-01 70175437
## 3 2002-09-01 61448422
## 4 2003-03-01 53751684
## 5 2003-10-01 40157554
## 6 2004-01-01 28780376
l <- lm(log(Cost.per.Genome) ~ Date, data=sequencing); summary(l)
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.969823683 1.433567932 35.5545 < 2.22e-16
## Date -0.002689621 0.000101692 -26.4486 < 2.22e-16
##
## Residual standard error: 0.889707 on 45 degrees of freedom
## Multiple R-squared: 0.939559, Adjusted R-squared: 0.938216
## F-statistic: 699.528 on 1 and 45 DF, p-value: < 2.22e-16
plot(log(Cost.per.Genome) ~ Date, data=sequencing)
## https://i.imgur.com/3XK8i0h.png
# as expected: linear in log (Moore’s law) 2002–2008, sudden drop, return to Moore’s law-ish ~December 2011?
# but on the other hand, maybe the post-December 2011 behavior is a continuation of the curve
library(segmented)
# 2 break-points / 3 segments:
piecewise <- segmented(l, seg.Z=~Date, psi=list(Date=c(13970, 16071)))
summary(piecewise)
## Estimated Break-Point(s):
## Est. St.Err
## psi1.Date 12680 1067.0
## psi2.Date 13200 279.8
##
## t value for the gap-variable(s) V: 0 0 2
##
## Meaningful coefficients of the linear terms:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 35.841699121 8.975628264 3.99322 0.00026387
## Date -0.001504431 0.000738358 -2.03754 0.04808491
## U1.Date 0.000679538 0.002057940 0.33020 NA
## U2.Date -0.002366688 0.001926528 -1.22847 NA
##
## Residual standard error: 0.733558 on 41 degrees of freedom
## Multiple R-Squared: 0.962565, Adjusted R-squared: 0.958
with(sequencing, plot(Date, log(Cost.per.Genome), pch=16)); plot(piecewise, add=T)
## https://i.imgur.com/HSRqkJO.png
# The first two segments look fine, but the residuals are clearly bad for the third line-segment:
# it undershoots (damaging the second segment's fit), overshoots, then undershoots again. Let's try again with more breakpoints:
lots <- segmented(l, seg.Z=~Date, psi=list(Date=NA), control=seg.control(stop.if.error=FALSE, n.boot=0))
summary(segmented(l, seg.Z=~Date, psi=list(Date=as.Date(c(12310, 12500, 13600, 13750, 14140, 14680, 15010, 15220), origin = "1970-01-01", tz = "EST"))))
# delete every breakpoint below t-value of ~|2.3|, for 3 breakpoints / 4 segments:
piecewise2 <- segmented(l, seg.Z=~Date, psi=list(Date=as.Date(c("2007-08-25","2008-09-18","2010-03-12"))))
with(sequencing, plot(Date, log(Cost.per.Genome), pch=16)); plot(piecewise2, add=T)
# the additional break-point is used up on a better fit in the curve. It looks like an exponential decay/asymptote,
# so let's work on fitting that part of the graph, the post-2007 curve:
sequencingRecent <- sequencing[sequencing$Date>as.Date("2007-10-01"),]
lR <- lm(log(Cost.per.Genome) ~ Date, data=sequencingRecent); summary(lR)
piecewiseRecent <- segmented(lR, seg.Z=~Date, psi=list(Date=c(14061, 16071))); summary(piecewiseRecent)
## Estimated Break-Point(s):
## Est. St.Err
## psi1.Date 14290 36.31
## psi2.Date 15290 48.35
##
## t value for the gap-variable(s) V: 0 0
##
## Meaningful coefficients of the linear terms:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.13831e+02 6.65609e+00 17.10182 2.0951e-13
## Date -7.13247e-03 4.73332e-04 -15.06865 2.2121e-12
## U1.Date 4.11492e-03 4.94486e-04 8.32161 NA
## U2.Date 2.48613e-03 2.18528e-04 11.37668 NA
##
## Residual standard error: 0.136958 on 20 degrees of freedom
## Multiple R-Squared: 0.995976, Adjusted R-squared: 0.994971
with(sequencingRecent, plot(Date, log(Cost.per.Genome), pch=16)); plot(piecewiseRecent, add=T)
lastPiece <- lm(log(Cost.per.Genome) ~ Date, data=sequencingRecent[as.Date(15290, origin = "1970-01-01", tz = "EST")<sequencingRecent$Date,]); summary(lastPiece)
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.012409648 1.875482507 9.07095 1.7491e-05
## Date -0.000531621 0.000119056 -4.46528 0.0020963
##
## Residual standard error: 0.0987207 on 8 degrees of freedom
## Multiple R-squared: 0.71366, Adjusted R-squared: 0.677867
with(sequencingRecent[as.Date(15290, origin = "1970-01-01", tz = "EST") < sequencingRecent$Date,],
plot(Date, log(Cost.per.Genome), pch=16)); abline(lastPiece)
predictDays <- seq(from=sequencing$Date[1], to=as.Date("2030-12-01"), by="month")
lastPiecePredict <- data.frame(Date = predictDays, Cost.per.Genome=c(sequencing$Cost.per.Genome, rep(NA, 305)), Cost.per.Genome.predicted = exp(predict(lastPiece, newdata = data.frame(Date = predictDays))))
nlmR <- nls(log(Cost.per.Genome) ~ SSasymp(as.integer(Date), Asym, r0, lrc), data=sequencingRecent); summary(nlmR)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## Asym 7.88908e+00 1.19616e-01 65.95328 <2e-16
## r0 1.27644e+08 1.07082e+08 1.19203 0.2454
## lrc -6.72151e+00 5.05221e-02 -133.04110 <2e-16
##
## Residual standard error: 0.150547 on 23 degrees of freedom
with(sequencingRecent, plot(Date, log(Cost.per.Genome))); lines(sequencingRecent$Date, predict(nlmR), col=2)
# side by side:
with(sequencingRecent, plot(Date, log(Cost.per.Genome), pch=16))
plot(piecewiseRecent, add=TRUE, col=2)
lines(sequencingRecent$Date, predict(nlmR), col=3)
# as we can see, the 3-piece linear fit and the exponential decay fit identically;
# but exponential decay is more parsimonious, IMO, so I prefer that.
predictDays <- seq(from=sequencingRecent$Date[1], to=as.Date("2020-12-01"), by="month")
data.frame(Date = predictDays, Cost.per.Genome.predicted = exp(predict(nlmR, newdata = data.frame(Date = predictDays))))https://www.unz.com/gnxp/the-intel-of-sequencing/#comment-677904 https://biomickwatson.wordpress.com/2015/03/25/the-cost-of-sequencing-is-still-going-down/
Genome sequencing historically has dropped in price ~18% per year. Consider this simple scenario: if we have a fixed amount of money to spend buying genomes, and we can afford to buy 1 genome in the first year, then the next year we can buy 1.21 genomes, then 1.48 genomes and so on and in 30 years we can afford to buy 385 genomes each year. The number we can afford in year x is:
sapply(0:30, function(x) 1/(0.82^x))
# [1] 1.000000000 1.219512195 1.487209994 1.813670724 2.211793566 2.697309227 3.289401497 4.011465240 4.892030780
# [10] 5.965891196 7.275477068 8.872533010 10.820162207 13.195319764 16.091853371 19.624211428 23.931965156 29.185323361
# [19] 35.591857758 43.404704583 52.932566564 64.551910444 78.721842005 96.002246348 117.075910180 142.775500220 174.116463682
# [28] 212.337150832 258.947744917 315.789932826 385.109674178Genomes are unlike computation, though, as they are data rather than an ephemeral service. Each genome is still useful and accumulates in a database. How many genomes total do we have each year? Quite a lot:
cumsum(sapply(0:30, function(x) 1/(0.82^x)))
# [1] 1.000000000 2.219512195 3.706722189 5.520392914 7.732186480 10.429495707 13.718897204 17.730362444
# [9] 22.622393224 28.588284420 35.863761488 44.736294497 55.556456704 68.751776468 84.843629839 104.467841268
# [17] 128.399806424 157.585129785 193.176987543 236.581692126 289.514258690 354.066169134 432.788011139 528.790257487
# [25] 645.866167667 788.641667886 962.758131569 1175.095282401 1434.043027318 1749.832960144 2134.942634322While initially there’s not much of a pile to concern ourselves with, eventually we have 200025ya+ genomes while still only producing <400 genomes that year, a factor of 5 difference. (As it happens, if you consider UKBB at n = 500k produced as a single investment 2012–52017, 23andMe in 2017 is reportedly n = 2-2.5m, so this 5x multiplier is about right.)
23andMe started back in 200718ya or so offering $1,583.86$1,0002007 SNP panels to a few thousand people, growing to ~1m by 8 years later in July 2015. To reproduce that in this model of constant investment we start with a base of 56k SNPs purchased per year, growing according to the cost decrease:
cumsum(sapply(0:7, function(x) (56000*1)/(0.82^x)))
# [1] 56000.0000 124292.6829 207576.4426 309142.0032 433002.4429 584051.7596 768258.2434 992900.2969What does that yield by 10 years later (2017) or 20 years later (2027)? It yields: 1.6m (1,600,943) and 16.2m (16,212,798) respectively.
Even if we assumed that annual genomes/SNPs leveled off in 2017, the linear increase pushes us into the millions range rapidly:
annualStagnation <- sapply(0:30, function(x) min(334089, (56000*1)/(0.82^x)))
cumsum(annualStagnation)
# [1] 56000.0000 124292.6829 207576.4426 309142.0032 433002.4429 584051.7596 768258.2434 992900.2969 1266854.0206 1600943.0206
# [11] 1935032.0206 2269121.0206 2603210.0206 2937299.0206 3271388.0206 3605477.0206 3939566.0206 4273655.0206 4607744.0206 4941833.0206
# [21] 5275922.0206 5610011.0206 5944100.0206 6278189.0206 6612278.0206 6946367.0206 7280456.0206 7614545.0206 7948634.0206 8282723.0206
# [31] 8616812.0206
data.frame(Year=2007:2037, total=round(totalStagnation))
# Year total
# 2007 56000
# 2008 124293
# 2009 207576
# 2010 309142
# 2011 433002
# 2012 584052
# 2013 768258
# 2014 992900
# 2015 1266854
# 2016 1600943
# 2017 1935032
# 2018 2269121
# 2019 2603210
# 2020 2937299
# 2021 3271388
# 2022 3605477
# 2023 3939566
# 2024 4273655
# 2025 4607744
# 2026 4941833
# 2027 5275922
# 2028 5610011
# 2029 5944100
# 2030 6278189
# 2031 6612278
# 2032 6946367
# 2033 7280456
# 2034 7614545
# 2035 7948634
# 2036 8282723
# 2037 8616812So even if no additional funds per year start getting spent on genomics despite the increasing utility and the cost curve remains the same, the cumulative number of SNPs or whole-genomes will increase drastically over the next 30 years. Genomes on their own have many uses, such as detecting human evolution, allowing better imputation panels, inferring population structure, counting variants, detecting particularly lethal mutations etc, but of course their main use is trait prediction. Given the increases, we would expect large enough n for Hsu’s lasso to undergo phase transition and recover nearly the full SNP heritability (see point-estimates for various traits); the bottleneck increasingly will not be genomes but phenotypic measurements.
Proposal: Hand-Counting Mobile App for More Fluid Group Discussions
Groups use voting for decision-making, but existing vote systems are cumbersome. Hand-raising is faster, but does not scale because hand-counting hands is slow. Advances in machine vision may make it possible for AI to count hands in photos accurately. Combined with a smartphone’s camera, this could yield an app for fast voting in even large groups.
Medium-large (>10 people) groups face a problem in reaching consensus: ballot or pen-and-paper voting is sufficiently slow and clunky that it is too costly to use for anything but the most important discussions. A group is forced to adopt other discussion norms and save a formal vote for only the final decision, and even then the long delay kills a lot of enthusiasm and interest. Voting could be used for many more decisions if it could be faster, and of course all existing group votes would benefit from increased speed. (I am reminded of anime conventions and film festivals where, particularly for short films such as AMVs, one seems to spend more time filling out a ballot & passing them along aisles & the staff painfully counting through each ballot by hand than one actually spends watching the media in question!)
It would be better if voting could be as fluent and easy as simply raising your hand like in a small group such as a classroom—a mechanism which makes it so easy to vote that votes can be held as fast as the alternatives can be spoken aloud and a glance suffices to count (an alert group could vote on 2 or 3 topics in the time it takes to read this sentence). But hand-raising, as great as it is, suffers from the flaw that it does not scale due to the counting problem: a group of 500 people can raise their hands as easily as a group of 50 or 5, but it takes far too long to count ~250 hands: the person counting will quickly tire of the tedium, they will make mistakes counting, and this puts a serious lag on each vote, a lag which increases linearly with the number of voters. (Hands can be easy to approximate if almost everyone votes for or against something, but if consensus is so overwhelming, one doesn’t need to vote in the first place! The hard case of almost-balanced votes is the most important case.)
One might suggest using an entirely different strategy: a website with HTML polls or little clicker gizmos like used in some college lectures to administer quick quizzes. This have the downsides that they require potentially expensive equipment (I used a clicker in one class and I think it cost at least $20, so if a convention wanted to use that in an audience of hundreds, that’s a major upfront cost & my experience was that clickers were unintuitive, did not always work, and slowed things down if anything; a website would only work if you assume everyone has smartphones and is willing to pull them out to use at an instance’s notice and of course that there’s working WiFi in the room, which cannot be taken for granted) and considerable overhead in explaining to everyone how it works and getting them on the same page and making sure every person who wanders in also gets the message. (If anyone is going to be burdened with understanding or using a new system, it should be the handful of conference/festival/group organizers, not the entire audience!) A simpler approach than hands would be specially-printed paper using, for example, QR codes like piCards, which can then be recognized by standard simple computer vision techniques; this is much cheaper than clickers but still requires considerable setup & inconvenience. It’s hard to imagine a film festival running using any system, and difficult to see these systems improving on pen-and-paper ballots which at least are cheap, relatively straightforward, and well-known.
Hand-counting really does seem like the best solution, if only the counting could be fixed. Counting is something computers do fast, so that is the germ of an idea. What if a smartphone could count the votes? You don’t want a smartphone app on the entire audiences’ phones, of course, since that’s even worse than having everyone go to a website to vote; but machine vision has made enormous strides in the 2000s-2010s, reaching human-equivalent performance on challenging image recognition contests like ImageNet. (Machine vision is complicated, but the important thing is that it’s the kind of complicated which can be outsourced to someone else and turned into a dead-easy-to-use app, and the burden does not fall on the primary users—the audience.) What if the organizer had an app which took a photo of the entire audience with lifted arms and counted hands & faces and returned a vote count in a second?
Such an app would be ideal for any cultural, political, or organizational meeting. Now the flow for, eg, a film festival could go: [no explanation given to audience, one just starts] “OK, how many people liked the first short, ‘Vampire Deli’ by Ms Houston?” [everyone raises hand, smartphone flashes, 1s passes] “OK, 140 votes. How many liked the second short, ‘Cthulicious’ by Mr Iouston?” [raises hands, smartphone flashes, 1s passes] “OK… 130 people. Congratulations Ms Houston!” And so on.
Such an app might be considered an infeasible machine vision task, but I believe it could be feasible: facial localization is an old and well-studied image recognition task (and effective algorithms are built into every consumer camera), hands/fingers have very distinct shapes, and both tasks seem easier than the subtle discriminations between, say, various dog breeds demanded of ImageNet contestants.
Specifically, one could implement the machine vision core as follows:
multilayer neural networks trained for one task can be repurposed to similar tasks by removing the highest layer and retraining on the new task, potentially reaping great performance gains as the hybrid network has already learned much of what it needs for the second task (“transfer learning”). So one could take a publicly available NN trained for ImageNet (such as AlexNet, available in caffe), remove the top two layers, and retrain on a dataset of audiences; this will perform better since the original NN has already learned how to detect edges, recognize faces, etc
The simpler task of counting crowds has already shown itself susceptible to deep learning: eg. “Cross-scene Crowd Counting via Deep Convolutional Neural Networks”.
raid Flickr and Google Images for CC-licensed photos of audiences raising their arms; then one can manually count how many arms are raised (or outsource to Amazon Mechanical Turk). With the boost from a transferred convolutional deep network, one might get good performance with just a few thousand photos to train with. If each photo takes a minute to obtain and count, then one can create a useful corpus in a week or two of work.
train the NN, applying the usual data augmentation tricks to increase one’s meager corpus, trying out random hyperparameters, tweaking the architecture, etc
(Note that while NNs are very slow and computationally intensive to train, they are typically quite fast to run; the smartphone app would not be training a NN, which is indeed completely infeasible from a CPU and battery life standpoint—it is merely running the NN created by the original developer.)
with an accurate NN, one can wrap it in a mobile app framework. The UI, at the simplest, is simply a big button to press to take a photo, feed it into the NN, and display the count. Some additional features come to mind:
“headcount mode”: one may not be interested in a vote, but in how many people are in an audience (to estimate how popular a guest is, whether an event needs to move to a new bigger space, etc). If the NN can count faces and hands to estimate a vote count, it can simply report the count of faces instead.
the app should save every photo & count, both as an audit trail and also to support post-vote recounts in case of disputes or a desire for a more definitive count
the reported count should come with an indication of the NN’s uncertainty/error-rate, so users are not misled by their little handheld oracle and so they can redo a vote if the choice is borderline; Bayesian methods, in which previous votes are drawn upon, might be relevant here.
if the original photo could be annotated with graphical notes for each recognized/counted hand & face, this would let the user ‘see’ what the NN is thinking and would help build confidence a great deal
it should support manually entering in a vote-count; if the manual count differs, then this indicates the NN made an error and the photo & count should be uploaded to the original developer so it can be added to the corpus and the NN’s performance fixed in future releases of the app
smartphone cameras may not be high-resolution or have a sufficiently wide field-of-view to capture the entire audience at once; some sort of “montage mode” should exist so the user can swing the phone across the audience, bursts of shots taken, and the overlapping photos stitched together into a single audience photo which can be then fed into the NN as usual
a burst of photos might be superior to a single photo due to smartphone & hand movement blur; I don’t know if it’s best to try to combine the photos, run the NN multiple times and take the median, or feed multiple photos into the NN (perhaps by moving to a RNN architecture?)
the full-strength NN might still be too slow and energy-hungry to run pleasantly on a smartphone; there are model compression techniques for simplifying deep NNs to reduce the number of nodes or have fewer layers without losing much performance, which might be useful in this context (and indeed, were originally motivated by wanting to make speech-recognition run better on smartphones)
Given this breakdown, one might estimate building such an app as requiring, assuming one is already reasonably familiar with deep networks & writing mobile apps:
1 week to find an ImageNet NN, learn how to modify it, and set it up to train on a fresh corpus
3 weeks to create a corpus of <5000 photos with manually-labeled hand counts
5 weeks to train the NN (NNs as large as ImageNet NNs take weeks to train; depending on the GPU hardware one has access to and how many tweaks and hyperparameters one tries, 5 weeks could be drastically optimistic; but on the plus side, it’s mostly waiting as the GPUs suck electricity like crazy)
5 weeks to make an intuitive simple app, submitting to an app store, etc
These estimates are loose and probably too optimistic (although I would be surprised if it took a good developer more than 6 months to develop this app), but that would suggest >14 weeks or 784 hours of work for a developer, start to finish. (Even at minimum wage, this represents a substantial development cost of >$6k; at more plausible developer salaries, easily >$60k of salary.)
How large is the market for such an app? Groups such as anime conventions or anything on a college campus are cheapskates and would balk at a price higher than $4.99 (even if only 5 or 10 staffers need to buy it and it makes the experience much smoother). There are probably several hundred anime or video game conventions which might use this to vote, so that might be 1000 sales there. There’s easily 13,000 business conventions or conferences in the USA, which might not need voting so much, but would be attracted by a headcount mode to help optimize their event. This suggests perhaps $70k in sales with much less profit after the app store cut & taxes, much of which sales would probably be one-offs as the user reuses it for each conference. So even a wild success, in which most events adopt use of such voting software, would barely recoup the development costs; as a product, it seems this is just too much of a niche unless one could develop it much faster (such as by finding an existing corpus of hands/photos, or be certain of banging out the mobile app in much less than I estimated), find a larger market (theaters for audience participation?), or increase price substantially (10x the price and aim at only businesses?).
Air Conditioner Replacement
Is my old air conditioner inefficient enough to replace? After calculating electricity consumption for it and a new air conditioner, with discounting, and with uncertainty in parameters evaluated by a Monte Carlo method, I conclude that the savings are too small by an order of magnitude to pay for a new replacement air conditioner.
I have an old Whirlpool air conditioner (AC) in my apartment, and as part of insulating and cooling my apartment, I’ve wondered if the AC should be replaced on energy efficiency grounds. Would a new AC save more than it costs upfront? What is the optimal decision here?
Initially I was balked in analysis because I couldn’t figure out what model it was, and thus anything about it like its energy efficiency. (No model number or name appears anywhere visible on it, and I’m not going to rip it out of the wall just to look at hidden parts.)
Parameters
So I began looking at all the old Whirlpool AC photographs in Google, and eventually I found one whose appearance exactly matches mine and which was released around when I think the AC was installed. The old AC is the “Whirlpool ACQ189XS” (official) (cost: $0, sunk cost), which is claimed to have an EER of 10.7.
For comparison, I browsed Amazon looking for highly-rated Energy Star AC models with at least 5000 BTU cooling power and costing $250-$300, picking out the Sunpentown WA-8022S 8000 BTU Window Air Conditioner ($271) with 11.3 EER. (Checking some other entries on Amazon, this is fairly representative on both cost & EER.)
Question: what is the electrical savings and hence the payback period of a new AC?
The efficiency unit here is the EER or energy efficiency ratio, defined as BTUs (amount of heat being moved by the AC) divided by watts consumed. Here we have ACs with 10.7 EER vs 11.2 EER; I need ~10k BTUs to keep the apartment cool (after fixing a lot of cracks, installing an attic fan and two box fans, putting tin foil over some windows, insulation under a floor etc), so the ACs will use up , and then x = 898 watts and 934 watts respectively.
(EER is a lot like miles per gallon/MPG as a measure of efficiency, and shares the same drawbacks: from a cost-perspective, EER/MPG don’t necessarily tell you what you want to know and can be misleading and harder to work with than if efficiency were reported as, say, gallons per mile. As watts per BTU or gallons per mile, it is easy to see that after a certain point, the cost differences have become absolutely small enough that improvements are not worth paying for. Going from 30 gallons of gas to 15 gallons of gas is worth more than going from 3 gallons to 1.5 gallons, even if the relative improvement is the same.)
So while operating, the two ACs will use 898 watts vs 934 watts or 0.89kWh vs 0.934kWh to cool; a difference of 36 watts or 0.036kWh.
Each kWh costs around $0.09 so the cost-difference is $0.00324 per hour.
AC is on May-September (5 months), and on almost all day although it only runs intermittently, so say a third of the day or 8 hours, for a total of 1200 hours of operation.
Cost-Benefit
Thus, then the annual benefit from switching to the new AC with 11.2 EER is or $3.9.
The cost is $271 amortized over n years. At $3.9 a year, it will take annually = 68 years to payback (ignoring breakage and discounting/interest/opportunity-cost). This is not good.
Decision: do not replace.
Discounting
To bring in discounting/interest: For what annual payment (cost-savings) would we be willing to pay the price of a new AC? More specifically, if it costs $271 and has an average payout period of 7 years, then at my usual annual discount rate of 5%, how much must each payout be?
r turns out to be ≥$46.83, which sounds about right. (Discounting penalizes future savings, so r should be greater than or $39, which it is.)
$47 is 12x larger than the estimated savings of $3.9, so the conclusion remains the same.
We could also work backward to figure out what EEC would justify an upgrade by treating it as an unknown e and solving for it; let’s say it must payback in 7 years (I doubt average AC lifetime is much longer) at least $271, with the same kWh & usage as before, what must the rival EEC be? as an equation:
and solving:
e > 20.02
I am pretty sure there are no ACs with EER>20!
Another way to look at it: if a new good AC costs ~$300 and I expect it to last ~7 years, then that’s an annual cost of $43. The current AC’s total annual cost to run is or . So it’s immediately clear that the energy savings must be huge—half!—before it can hope to justify a new purchase.
Sensitivity Analysis
The above analyses were done with point-estimates. It’s only fair to note that there’s a lot of uncertainty lurking in those estimates: $0.09 was just the median of the estimates I found for my state’s electricity rates, the AC might be on 4 or 6 months, the hours per day might be considerably higher (or lower) than my guess of 8 hours, 10.7 & 11.2 EERs are probably best-case estimates and the real efficiencies lower (they’re always lower than nominal), the discount rate may be a percent lower or higher and so minimum savings would be off by as much as $4 in either direction, and so on. It would be good to do a bit of a sensitivity analysis to make sure that this is not being driven by any particular number. (Based on the definition, since it’s using mostly multiplication, the final value should be robust to considerable error in estimating each parameter, but you never know.) Throwing together my intuition for how much uncertainty is in each parameter and modeling most as normals, I can simulate my prior distribution of savings:
set.seed(2015-07-26)
simulate <- function() {
BTUs <- rnorm(1, 10000, 100)
EER_old <- 10.7 - abs(rnorm(1, 0, 0.5)) # half-normals because efficiencies only get worse, not better
EER_new <- 11.2 - abs(rnorm(1, 0, 0.5))
kWh <- rnorm(1, 0.09, 0.01)
dailyUsage <- rnorm(1, 8, 2)
months <- sample (4:6, 1)
minimumSavings <- rnorm(1, 47, 4)
annualNetSavings <- ((((BTUs / EER_old ) - (BTUs / EER_new)) / 1000) * kWh * dailyUsage * 30 * months) - minimumSavings
return(annualNetSavings)
}
sims <- replicate(100000, simulate())
summary(sims)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -70.3666500 -46.2051500 -42.3764100 -42.1133700 -38.3134600 -0.7334517
quantile(sims, p=c(0.025, 0.975))
## 2.5% 97.5%
## -53.59989114 -29.13999204Under every simulation, a new AC is a net loss. (Since we have no observed data to update our priors with, this is an exercise in probability, not Bayesian inference, and so there is no need to bring in JAGS.)
There are two choices: replace or not. The expected-value of a replacement is or −$42, and the expected-value of not replacing is or $0; the latter is larger than the former, so we should choose the latter and not replace the old AC.
Hence we can be confident that not getting a new AC really is the right decision.
Some Ways of Dealing With Measurement Error
Prompted by a question on LessWrong, some examples of how to analyze noisy measurements in R:
## Create a simulated dataset with known parameters, and then run a ML multilevel model, a ML SEM, &
## a Bayesian multilevel model; with the last, calculate Expected Value of Sample Information (EVSI):
## SIMULATE
set.seed(2015-08-11)
## "There is a variable X, x belongs to [0, 100]."
toplevel <- rnorm(n=1, 50, 25)
## "There are n ways of measuring it, among them A and B are widely used."
## "For any given measurer, the difference between x(A) and x(B) can be up to 20 points."
A <- toplevel + runif(1, min=-10, max=10)
B <- toplevel + runif(1, min=-10, max=10)
c(toplevel, A, B)
# [1] 63.85938385 55.43608379 59.42333264
### the true level of X we wish to recover is '63.85'
## "Between two any measurers, x(A)1 and x(A)2 can differ on average 10 points, likewise with B."
### let's imagine 10 hypothetical points are sample using method A and method B
### assume 'differ on average 10 points' here means something like 'the standard deviation is 10'
A_1 <- rnorm(n=10, mean=A, sd=10)
B_1 <- rnorm(n=10, mean=B, sd=10)
data <- rbind(data.frame(Measurement="A", Y=A_1), data.frame(Measurement="B", Y=B_1)); data
# Measurement Y
# 1 A 56.33870025
# 2 A 69.07267213
# 3 A 40.36889573
# 4 A 48.67289213
# 5 A 79.92622603
# 6 A 62.86919410
# 7 A 53.12953462
# 8 A 66.58894990
# 9 A 47.86296948
# 10 A 60.72416003
# 11 B 68.60203507
# 12 B 58.24702007
# 13 B 45.47895879
# 14 B 63.45308935
# 15 B 52.27724328
# 16 B 56.89783535
# 17 B 55.93598486
# 18 B 59.28162022
# 19 B 70.92341777
# 20 B 49.51360373
## MLM
## multi-level model approach:
library(lme4)
mlm <- lmer(Y ~ (1|Measurement), data=data); summary(mlm)
# Random effects:
# Groups Name Variance Std.Dev.
# Measurement (Intercept) 0.0000 0.000000
# Residual 95.3333 9.763877
# Number of obs: 20, groups: Measurement, 2
#
# Fixed effects:
# Estimate Std. Error t value
# (Intercept) 58.308250 2.183269 26.70685
confint(mlm)
# 2.5 % 97.5 %
# .sig01 0.000000000 7.446867736
# .sigma 7.185811525 13.444112087
# (Intercept) 53.402531768 63.213970887
## So we estimate X at 58.3 but it's not inside our confidence interval with such little data. Bad luck?
## SEM
library(lavaan)
X.model <- ' X =~ B + A
A =~ a
B =~ b'
X.fit <- sem(model = X.model, meanstructure = TRUE, data = data2)
summary(X.fit)
# ... Estimate Std.err Z-value P(>|z|)
# Latent variables:
# X =~
# B 1.000
# A 7619.504
# A =~
# a 1.000
# B =~
# b 1.000
#
# Intercepts:
# a 58.555
# b 58.061
# X 0.000
# A 0.000
# B 0.000
## Well, that didn't work well - explodes, unfortunately. Probably still not enough data.
## MLM (Bayesian)
library(R2jags)
## rough attempt at writing down an explicit multilevel model which
## respects the mentioned priors about errors being reasonably small:
model <- function() {
grand.mean ~ dunif(0,100)
delta.between.group ~ dunif(0, 10)
sigma.between.group ~ dunif(0, 100)
tau.between.group <- pow(sigma.between.group, -2)
for(j in 1:K){
# let's say the group-level differences are also normally-distributed:
group.delta[j] ~ dnorm(delta.between.group, tau.between.group)
# and each group also has its own standard-deviation, potentially different from the others':
group.within.sigma[j] ~ dunif(0, 20)
group.within.tau[j] <- pow(group.within.sigma[j], -2)
# save the net combo for convenience & interpretability:
group.mean[j] <- grand.mean + group.delta[j]
}
for (i in 1:N) {
# each individual observation is from the grand-mean + group-offset, then normally distributed:
Y[i] ~ dnorm(grand.mean + group.delta[Group[i]], group.within.tau[Group[i]])
}
}
jagsData <- list(N=nrow(data), Y=data$Y, K=length(levels(data$Measurement)),
Group=data$Measurement)
params <- c("grand.mean","delta.between.group", "sigma.between.group", "group.delta", "group.mean",
"group.within.sigma")
k1 <- jags(data=jagsData, parameters.to.save=params, inits=NULL, model.file=model); k1
# ... mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
# delta.between.group 4.971 2.945 0.221 2.353 4.967 7.594 9.791 1.008 260
# grand.mean 52.477 11.321 23.453 47.914 53.280 58.246 74.080 1.220 20
# group.delta[1] 6.017 11.391 -16.095 0.448 5.316 10.059 34.792 1.152 21
# group.delta[2] 5.662 11.318 -15.836 0.054 5.009 10.107 33.548 1.139 21
# group.mean[1] 58.494 3.765 50.973 56.188 58.459 60.838 66.072 1.001 3000
# group.mean[2] 58.139 2.857 52.687 56.366 58.098 59.851 63.999 1.003 920
# group.within.sigma[1] 12.801 2.766 8.241 10.700 12.446 14.641 18.707 1.002 1100
# group.within.sigma[2] 9.274 2.500 5.688 7.475 8.834 10.539 15.700 1.002 1600
# sigma.between.group 18.031 21.159 0.553 3.793 9.359 23.972 82.604 1.006 1700
# deviance 149.684 2.877 145.953 147.527 149.081 151.213 156.933 1.001 3000
## VOI
posteriorXs <- k1$BUGSoutput$sims.list[["grand.mean"]]
MSE <- function(x1, x2) { (x2 - x1)^2 }
lossFunction <- function(x, predictions) { mean(sapply(predictions, function(x2) { MSE(x, x2)}))}
## our hypothetical mean-squared loss if we predicted, say, X=60:
lossFunction(60, posteriorXs)
# [1] 184.7087612
## of the possible values for X, 1-100, what value of X minimizes our squared error loss?
losses <- sapply(c(1:100), function (n) { lossFunction(n, posteriorXs);})
which.min(losses)
# [1] 52
## 52 also equals the mean estimate of X, which is good since it's well known that the mean is what minimizes
## the loss when the loss is squared-error so it suggests that I have not screwed up the definitions
losses[52]
[1] 128.3478462
## to calculate EVSI, we repeatedly simulate a few hundred times the existence of a hypothetical 'C' measurement
## and draw n samples from it;
## then we add the C data to our existing A & B data; run our Bayesian multilevel model again on the bigger dataset;,
## calculate what the new loss is, and compare it to the old loss to see how much the new data
## reduced the loss/mean-squared-error.
## Done for each possible n (here, 1-30) and averaged out, this tells us how much 1 additional datapoint is worth,
## 2 additional datapoints, 3 additional datapoints, etc.
sampleValues <- NULL
for (i in seq(from=1, to=30)) {
evsis <- replicate(500, {
n <- i
C <- toplevel + runif(1, min=-10, max=10)
C_1 <- rnorm(n=n, mean=C, sd=10)
## all as before, more or less:
newData <- rbind(data, data.frame(Measurement="C", Y=C_1))
jagsData <- list(N=nrow(newData), Y=newData$Y, K=length(levels(newData$Measurement)),
Group=newData$Measurement)
params <- c("grand.mean","delta.between.group", "sigma.between.group", "group.delta", "group.mean",
"group.within.sigma")
jEVSI <- jags(data=jagsData, parameters.to.save=params, inits=NULL, model.file=model)
posteriorTimesEVSI <- jEVSI$BUGSoutput$sims.list[["grand.mean"]]
lossesEVSI <- sapply(c(1:100), function (n) { lossFunction(n, posteriorTimesEVSI);})
oldOptimum <- 128.3478462 # losses[52]
newOptimum <- losses[which.min(lossesEVSI)]
EVSI <- newOptimum - oldOptimum
return(EVSI)
}
)
print(i)
print(mean(evsis))
sampleValues[i] <- mean(evsis)
}
sampleValues
# [1] 13.86568780 11.07101087 14.15645538 13.05296681 11.98902668 13.86866619 13.65059093 14.05991443
# [9] 14.80018511 16.36944874 15.47624541 15.64710237 15.74060632 14.79901214 13.36776390 15.35179426
# [17] 14.31603459 13.70914727 17.20433606 15.89925289 16.35350861 15.09886204 16.30680175 16.27032067
# [25] 16.30418553 18.84776433 17.86881713 16.65973397 17.04451609 19.17173439
## As expected, the gain in reducing MSE continues increasing as data comes in but with diminishing returns;
## this is probably because in a multilevel model like this, you aren't using the _n_ datapoints to estimate X
## directly so much as you are using them to estimate a much smaller number of latent variables, which are then
## the _n_ used to estimate X. So instead of getting hyperprecise estimates of A/B/C, you need to sample from additional
## groups D/E/F/... Trying to improve your estimate of X by measuring A/B/C many times is like trying to estimate
## IQ precisely by administering a WM test a hundred times.
## If we wanted to compare with alternatives like instead sampling n data points from C and a D, it's easy to modify
## the EVSI loop to do so: generate `D <- toplevel + runif(1, min=-10, max=10); D_1 <- rnorm(n=n, mean=D, sd=10)`
## and now `rbind` D_1 in as well. At a guess, after 5-10 samples from the current group, estimates of X will be improved more
## by then sampling from a new group.
## Or the loss function could be made more realistic. It's unlikely one is paid by MSE, and if one adds in how much
## money each sample costs, with a realistic loss function, one could decide exactly how much data is optimal to collect.
## To very precisely estimate X, when our measurements are needed to measure at least 3 latent variables,
## requires much more data than usual.
## In general, we can see the drawbacks and benefits of each approach. A canned MLM
## is very fast to write but doesn't let us include prior information or easily run
## additional analyses like how much additional samples are worth. SEM works poorly
## on small samples but is still easy to write in if we have more complicated
## models of measurement error. A full-blown modeling language like JAGS is quite
## difficult to write in and MCMC is slower than other approaches but handles small
## samples without any errors or problems and offers maximal flexibility in using
## the known prior information and then doing decision-theoretic stuff. Overall for
## this problem, I think JAGS worked out best, but possibly I wasn't using LAVAAN
## right and that's why SEM didn't seem to work well.Value of Information: Clinical Prediction Instruments for Suicide
https://slatestarcodex.com/2015/08/31/magic-markers/
I agree. When criticizing the study for claiming the blood levels added predictive power and it’s not clear they did, this is solely a statistical claim and can be done in a vacuum. But when one then goes on to pan the predictive power of the underlying clinical prediction instruments as useless in all circumstances, based on just the prediction stats:
So when people say “We have a blood test to diagnose suicidality with 92% accuracy!”, even if it’s true, what they mean is that they have a blood test which, if it comes back positive, there’s still less than 50-50 odds the person involved is suicidal. Okay. Say you’re a psychiatrist. There’s a 48% chance your patient is going to be suicidal in the next year. What are you going to do? Commit her to the hospital? I sure hope not. Ask her some questions, make sure she’s doing okay, watch her kind of closely? You’re a psychiatrist and she’s your depressed patient, you would have been doing that anyway. This blood test is not really actionable. And then remember that this isn’t the blood test we have. We have some clinical prediction instruments that do this…But having “a blood test for suicide” won’t be very useful, even if it works.
One is implicitly making some strong cost-benefit claims here and stepping from statistics (‘what are the probabilities?’) to decision theory (‘given these probabilities, how should I act?’). They are not identical: no AUC graph will ever tell you if a model’s predictions are useful or not, and there is no universal threshold where 92% specificity/sensitivity is totally useless but 95% would make a difference—these clinical prediction instruments might be useless indeed, but that will depend on costs, base rates, and available actions. (I tried to make this point to Coyne on Twitter earlier but I don’t think he understood what I was getting at & he blew me off.)
Discontinuities come from our actions; our inferences are incremental. There are some contexts where a tiny 1% improvement in AUC might be worth a lot (Wall Street) and there are some contexts where sensitivity or specificity of 99% is still useless because it won’t change your actions at all (I’m currently comparing my riding lawn mower to a robotic lawn mower, and thus far, it doesn’t matter how precise my parameters are, the robotic lawn mowers are, to my disappointment, just too expensive right now). I think p-values have shown us how well arbitrary thresholds work out in practice (and remember where they came from in the first place! decision rules set per problem—Gosset, in optimizing a brewery, did not have the pathologies we have with p<0.05 fetishism.) I also don’t believe your choices are really that restricted: you mean if you were absolutely convinced that your patient was about to commit suicide, there is absolutely nothing you could do besides treat them like any other depressive? That seems unlikely. But whatever, even if commitment is the only alternative, there is still a value to the information provided by a clinical prediction instrument, and we can calculate it, and you should if you want to rule it out as having any value, in the same way that in criticizing a study as weak, it’s better to ignore the p-values and just work out the right posterior and demonstrate directly how little evidence it contains.
Let’s try this as an example, it’s not hard or terribly complex (just tedious). So we have a ward of 100 depressive patients where we are interested in preventing suicide; our prior probability is that 7.5% or ~7 of them will commit suicide. The value of a life has been given a lot of different valuations, but $10 million is a good starting point.
Action 1:
What are our costs or losses? We could say that we expect a loss of 7.5*$10m or −$75m, and if we stand by and do no treatment or intervention whatsoever, we spend no more money and so the total loss is
0 + 0.075 * 100 * 10,000,000 = −$75,000,000
Action 2:
Let’s say they all stay by default for one week and this costs a net $1,000 a day; let’s say further that, since commitment is the mentioned alternative, while committed a suicide attempt will fail. And since we know that suicides are so often spontaneous and major depression comes and goes, a frustrated suicide attempt doesn’t simply mean that they will immediately kill themselves as soon as they get out. This 7% comes from a followup period of a year, so the probability any will attempt suicide in the next week might be 0.075/52 or 0.001442307692. So this gives us our default setup: we have 100 patients staying for 7 days at a net cost of $1,000 a day or $700,000 total, and by having them stay, we stop an expected average of 0.14 suicides and thus we prevent an expected loss of 0.14 * $10m = $1,440,000, for a total loss of treatment-cost minus treatment-gain plus remaining-loss:
$700,000 - (0.14 * $10m) - $10m * 100 * (0.075-(0.075/52)) = −$74,257,692.
Note that this loss is smaller than in the scenario in which we don’t do any commitment at all; since one week of suicide-watch reduced the suicide loss more than it cost, this is not surprising.
Specifically, the benefit is:
action1 - action2 = gain to switching 75000000 - 74257692 = $742,308
Not fantastic, but it’s in the right order of magnitude (you can’t expect more from a low base-rate event and a treatment with such a low probability of making a difference, after all) so it looks plausible, and it’s still more than zero. We can reject the action of not committing them at all as being inferior to committing them for one week.
Action 3:
What if we were instead choosing between one week and committing them for a full year—thus catching the full 7.5% of suicides during the 1-year followup? Does that work? First, the loss from this course of action:
((100*365.2*1000) - (0 * 10000000) - (10000000 * 100 * (0.075-(0.075/1)))) = −$36,520,000
Since there are no suicides, we avoid the default loss of −$75m, but we still have to spend $36,520,000 to pay for the long-term commitment. However, the benefit to the patients has increased dramatically since we stop so many more suicides:
action 2 - action 3 = $35,637,692.31
(We go from a loss of −$74m to a loss of −$36m.) So we see action 3 is even better than action 2 for the patients. Of course, we can’t extrapolate out any further than 1 year, because that’s what our followup number is, and we don’t know how the suicide risk falls after the 1 year point—if it drops to ~0, then further commitment is a terrible idea. So I’m not going to calculate out any further. (Since this is all linear stuff, the predicted benefit will increase smoothly over the year and so there’s no point in calculating out alternatives like 1 month, 3 months, 6 months, 9 months, etc.) What’s that, action 3 is totally infeasible and no one would ever agree to this—the patients would scream their heads off and the health insurance companies would never go for it—even if we could show that long commitments do reduce the suicide rate enough to justify the costs? And, among other things, I’ve oversimplified in assuming the 7% risk is evenly distributed over the year rather than a more plausible distribution like exponentially decreasing from Day 1, so likely commitment stops being a good idea more like month 3 or something? Yeah, you’re probably right, so let’s go back to using action 2’s loss as our current best alternative.
Now, having set out some of the choices available, we can find out how much better information is worth. First, let’s ask what the Expected Value of Perfect Information is: if we were able to take our 100 patients and exactly predict which 7 were depressive and would commit suicide this year in the absence of any intervention, where our choice is between committing them for one week or not at all. Given such information we can eject the 93 who we now know were never a suicide risk, and we hold onto the 7 endangered patients, and we have a new loss of the commitment cost of 7 people for a week vs the prevented loss of the chance they will try to commit suicide that week of this year:
((771000) - (0.14 * 10000000) - (10000000 * 7 * (1-(1/52)))) = −$70,004,846
How much did we gain from our perfect information? About $4m:
74257692 - 70004846 = $4,252,846
(This passes our sanity checks: additional information should never hurt us, so the amount should be >=$0, but we are limited by the intervention to doing very little, so the ceiling should be a low amount compared to the total loss, which this is.)
So as long as the perfect information did not cost us more than $4m or so, we would have net gained from it: we would have been able to focus commitment on the patients at maximal risk. So suppose we had a perfect test which cost $1,000 a patient to run, and we wanted to know if the gained information was valuable enough to bother with using this expensive test; the answer in this case is definitely yes: with 100 patients, it’ll cost $100,000 to run the test but it’ll save $4.25m for a net profit of $4.15m. In fact, we would be willing to pay per-patient costs up to $42k, at which point we hit break-even (4252846 / 100).
OK, so that’s perfect information. What about imperfect information? Well, imperfect is a lot like perfect information, just, y’know—less so. Let’s consider this test: with the same prior, a negative on it means the patient now has P=0.007 to commit suicide that year, and a positive means P=0.48, and the sensitivity/specificity at 92%. (Just copying that from OP & ButYouDisagree, since those sound plausible.) So when we run the test on our patients, we find of the 4 possible outcomes:
85.1 patients are non-suicidal and the test will not flag them
7.4 are non-suicidal but the test will flag them
6.9 are suicidal and the test will flag them
0.6 are suicidal but the test will not flag them
So if we decide whether to commit or not commit solely based on this test, we will send home 85.1 + 0.6 = 85.7 patients (and indeed 0.6/85.7=0.007), and we will retain the remaining 7.4 + 6.9 = 14.3 patients (and indeed, 6.9/14.3=0.48). So our loss is the wrongly ejected patient of 0.6 suicides plus the cost of committing 14.3 patients (both safe and at-risk) for a week in exchange for the gain of a small chance of stopping the suicide of the 6.9 actually at risk:
(10000000*85.7*0.007) + (14.3*7*1000) + (10000000 * (0.4814.3) (1-(1/52))) = −$73,419,100
How much did we gain from our imperfect information? About $0.8m:
74257692 - 73419100 = $838,592
or $8,385.92 per patient. (This passes our sanity check: greater than $0, but much less than the perfect information. The exact amount may seem lame, but as a fraction of the value of perfect information, it’s not too bad: the test gets us 20% - 838592 / 4252846 - of the way to perfection.)
And that’s our answer: the test is not worth $0—it’s worth $8k. And once you know what the cost of administering the test is, you simply subtract it and now you have the Net Expected Value of Information for this test. (I can’t imagine it costs $8k to administer what this sounds like, so at least in this model, the value is highly likely >$0.)
By taking the posterior of the test and integrating all the estimated costs and benefits into a single framework, we can nail down exactly how much value these clinical instruments could deliver if used to guide decision-making. And if you object to some particular parameter or assumption, just build another decision-theory model and estimate the new cost. For example, maybe commitment actually costs, once you take into account all the disruption to lives and other such side-effects, not $1,000 but net of $5,000 per day, what then? Then the gain halves to $438,192, etc. And if it costs $1,0000 then the test is worth nothing because you won’t commit anyone ever because it’s just way too expensive, and now you know it’s worth $0; or if commitment is so cheap that it’s more like $100 a day, then the test is also worth $0 because you would just commit everyone (since breakeven is then a suicide probability way below 7%, all the way at ~0.4% which is still below the 0.7% which the test can deliver, so the test result doesn’t matter for deciding whether to commit, so it’s worth $0), or if you adopt a more reasonable value of life like $20m, the value of perfect information shoots up (obviously, since the avoided loss doubles) but the value of imperfect information drops like a stone (since now that one suicidal patient sent home blows away your savings from less committing) and the test becomes worthless; and playing with the formulas, you can figure out the various ranges of assumptions in which the test has positive value and estimate how much it has under particular parameters, and of course if parameters are uncertain, you can cope with that uncertainty by embedding this in a Bayesian model to get posterior distributions of particular parameters incorporating all the uncertainty.
So to sum up: there are no hard thresholds in decision-making and imposing them can cost us better decision-making, so to claim additional information is worthless, more analysis needed, and this analysis must be done with respect to the available actions & their consequences, which even under the somewhat extreme conditions here of very weak interventions & low base-rates, suggests that the value of this information is positive.
Bayesian Model Averaging
## original: "Bayesian model choice via Markov chain Monte Carlo methods" Carlin & Chib 1995 https://www.ma.imperial.ac.uk/~das01/MyWeb/SCBI/Papers/CarlinChib.pdf
## Kobe example & data from: "A tutorial on Bayes factor estimation with the product space method", Lodewyckx et al 2011 https://ejwagenmakers.com/2011/LodewyckxEtAl2011.pdf
## Lodewyckx code can be downloaded after registration & email from https://ppw.kuleuven.be/okp/software/scripts_tut_bfepsm/
## "Table 2: Observed field goals (y) and attempts (n) by Kobe Bryant during the NBA seasons of 1999 to 2006."
kobe <- read.csv(stdin(),header=TRUE)
Year, y, n, y.n
1999, 554, 1183, 0.47
2000, 701, 1510, 0.46
2001, 749, 1597, 0.47
2002, 868, 1924, 0.45
2003, 516, 1178, 0.44
2004, 573, 1324, 0.43
2005, 978, 2173, 0.45
2006, 399, 845, 0.47
library(runjags)
model1 <- "model{
# 1. MODEL INDEX
# Model index is 1 or 2.
# Prior probabilities based on argument prior1.
# Posterior probabilities obtained by averaging
# over postr1 and postr2.
M ~ dcat(p[])
p[1] <- prior1
p[2] <- 1-prior1
postr1 <- 2-M
postr2 <- 1-postr1
# 2. MODEL LIKELIHOOD
# For each year, successes are Binomially distributed.
# In M1, the success rate is fixed over years.
# In M2, the success rate is year-specific.
for (i in 1:n.years){
successes[i] ~ dbin(pi[M,i], attempts[i])
pi[1,i] <- pi.fixed
pi[2,i] <- pi.free[i]
}
# 3. MODEL 1 (one single rate)
# The fixed success rate is given a Beta prior and pseudoprior.
# Whether it is a prior or pseudoprior depends on the Model index.
pi.fixed ~ dbeta(alpha.fixed[M],beta.fixed[M])
alpha.fixed[1] <- alpha1.prior
beta.fixed[1] <- beta1.prior
alpha.fixed[2] <- alpha1.pseudo
beta.fixed[2] <- beta1.pseudo
# 4. MODEL 2 (multiple independent rates)
# The year-specific success rate is given a Beta prior and pseudoprior.
# Whether it is a prior or pseudoprior depends on the Model index.
for (i in 1:n.years){
pi.free[i] ~ dbeta(alpha.free[M,i],beta.free[M,i])
alpha.free[2,i] <- alpha2.prior
beta.free[2,i] <- beta2.prior
alpha.free[1,i] <- alpha2.pseudo[i]
beta.free[1,i] <- beta2.pseudo[i]
}
# predictive interval for hypothetical 2007 data in which Kobe makes 1000 shots:
successes.new.1 ~ dbin(pi.fixed, 1000)
successes.new.2 ~ dbin(pi.free[n.years], 1000)
# success.new.weighted ~ dcat(M)
}"
# 'prior1' value from paper
data <- list("prior1"=0.000000007451, "n.years"= length(kobe$Year), "successes"=kobe$y, "attempts"=kobe$n,
"alpha1.prior"=1, "beta1.prior"=1, "alpha2.prior"=1, "beta2.prior"=1,
"alpha1.pseudo"=1, "beta1.pseudo"=1, "alpha2.pseudo"=rep(1,8), "beta2.pseudo"=rep(1,8) )
# inits <- function() { list(mu=rnorm(1),sd=30,t=as.vector(apply(mailSim,1,mean))) }
params <- c("pi.free", "pi.fixed", "postr1", "postr2", "M", "successes.new.1", "successes.new.2")
j1 <- run.jags(model=model1, monitor=params, data=data, n.chains=getOption("mc.cores"), method="rjparallel", sample=500000); j1
# JAGS model summary statistics from 4000000 samples (chains = 8; adapt+burnin = 5000):
#
# Lower95 Median Upper95 Mean SD Mode MCerr MC%ofSD SSeff
# pi.free[1] 0.3145 0.46864 0.98709 0.47383 0.11553 ---0.00041958 0.4 75810
# pi.free[2] 0.10099 0.46447 0.77535 0.47005 0.1154 ---0.00042169 0.4 74887
# pi.free[3] 0.19415 0.4692 0.86566 0.4741 0.11457 ---0.00040171 0.4 81342
# pi.free[4] 0.020377 0.45146 0.69697 0.45867 0.11616 ---0.00042696 0.4 74023
# pi.free[5] 0.024472 0.43846 0.7036 0.44749 0.11757 ---0.00043352 0.4 73548
# pi.free[6] 0.076795 0.43325 0.74944 0.44318 0.11684 ---0.00043892 0.4 70863
# pi.free[7] 0.06405 0.45033 0.73614 0.45748 0.11541 ---0.00041715 0.4 76543
# pi.free[8] 0.30293 0.47267 0.97338 0.47708 0.11506 ---0.00040938 0.4 79000
# pi.fixed 0.039931 0.45756 0.97903 0.49256 0.26498 ---0.00099537 0.4 70868
# postr1 0 0 1 0.15601 0.36287 0 0.15113 41.6 6
# postr2 0 1 1 0.84399 0.36287 1 0.15113 41.6 6
# M 1 2 2 1.844 0.36287 2 0.15113 41.6 6
# successes.new.1 0 463 940 492.57 265.28 454 0.99543 0.4 71019
# successes.new.2 300 473 971 477.05 116.03 473 0.4152 0.4 78094
getLogBF <- function(prior0, postr0) { log((postr0/(1-postr0)) / (prior0/(1-prior0))) }
getLogBF(0.000000007451, 0.15601)
# [1] 17.02669704
## analytic BF: 18.79; paper's MCMC estimate: 18.80; not sure where I lost 1.8 of the BF.Dealing With All-Or-Nothing Unreliability of Data
Given two disagreeing polls, one small & imprecise but taken at face-value, and the other large & precise but with a high chance of being totally mistaken, what is the right Bayesian model to update on these two datapoints? I give ABC and MCMC implementations of Bayesian inference on this problem and find that the posterior is bimodal with a mean estimate close to the large unreliable poll’s estimate but with wide credible intervals to cover the mode based on the small reliable poll’s estimate.
A question was asked of me: what should one infer if one is given what would be definitive data if one could take it at face value—but one suspects this data might be totally 100% incorrect? An example would be if one wanted to know what fraction of people would answer ‘yes’ to a particular question, and one had a very small poll (n = 10) suggesting 90% say yes, but then one was also given the results from a much larger poll (n = 1000) saying 75% responded yes—but this poll was run by untrustworthy people, people that, for whatever reason, you believe might make something up half the time. You should be able to learn something from this unreliable poll, but you can’t learn everything from it because you would be burned half the time.
If not for this issue of unreliability, this would be an easy binomial problem: specify a uniform or Jeffreys prior on what percentage of people will say yes, add in the binomial data of 9⁄10, and look at the posterior. But what do we do with the unreliability joker?
Binomial
First let’s try the simple case, just updating on a small poll of 9⁄10. We would expect it to be unimodally peaked around 80-90%, but broad (due to the small sample size) and falling sharply until 100% since being that high is a priori unlikely.
MCMC using Bayesian First Aid:
## install.packages("devtools")
## devtools::install_github("rasmusab/bayesian_first_aid")
library(BayesianFirstAid)
b <- bayes.binom.test(oldData$Yes, oldData$N); b
# ...number of successes = 9, number of trials = 10
# Estimated relative frequency of success:
# 0.85
# 95% credible interval:
# 0.63 0.99
# The relative frequency of success is more than 0.5 by a probability of 0.994
# and less than 0.5 by a probability of 0.006Which itself is a wrapper around calling out to JAGS doing something like this:
library(runjags)
model_string <- "model {
x ~ dbinom(theta, n)
theta ~ dbeta(1, 1) }"
model <- autorun.jags(model_string, monitor="theta", data=list(x=oldData$Yes, n=oldData$N)); model
# JAGS model summary statistics from 20000 samples (chains = 2; adapt+burnin = 5000):
#
# Lower95 Median Upper95 Mean SD Mode MCerr MC%ofSD SSeff AC.10 psrf
# theta 0.63669 0.85254 0.9944 0.83357 0.10329 ---0.0007304 0.7 20000 0.011014 1.0004Here is a simulation-based version of Bayesian inference using ABC:
oldData <- data.frame(Yes=9, N=10)
simulatePoll <- function(n, pr) { rbinom(1, size=n, p=pr); }
poll_abc <- replicate(100000, {
# draw from our uniform prior
p <- runif(1,min=0,max=1)
# simulate a hypothetical poll dataset the same size as our original
newData <- data.frame(Yes=simulatePoll(oldData$N, p), N=oldData$N)
# were they equal? if so, save sample as part of posterior
if (all(oldData == newData)) { return(p) }
}
)
resultsABC <- unlist(Filter(function(x) {!is.null(x)}, poll_abc))
summary(resultsABC)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.3260816 0.7750520 0.8508855 0.8336383 0.9117471 0.9991691
hist(resultsABC)
# https://i.imgur.com/fn3XYQW.pngThey look identical, as they should.
Binomial With Binary Unreliability
To implement our more complicated version: the original poll remains the same but we add in the complication of a very large poll which 50% of the time is a true measure of the poll response and 50% of the time is drawn uniformly at random. (So if the true poll response is 90%, then half the time the large poll will yield accurate data like 905/1,000 or 890/1,000, and the rest it will yield 10/1,000 or 400/1,000 or 700/1,000.) This is different from the more common kinds of measurement-error models where it’s generally assumed that the noisy measurements still have some informativeness to them; here there is none.
Specifically, this faux poll has yielded the data not 9⁄10, but 750/1,000.
ABC
Using ABC again: we generate the reliable small poll as before, and we add in an faux poll where we flip a coin to decide if we are going to return a ‘yes’ count based on the population parameters or just a random number, then we combine the two datasets and check that it’s identical to the actual data, saving the population probability if it is.
oldData2 <- data.frame(Yes=c(9,750), N=c(10,1000)); oldData2
# Yes N
# 1 9 10
# 2 750 1000
simulateHonestPoll <- function(n, pr) { rbinom(1, size=n, p=pr); }
simulateFauxPoll <- function(n, pr, switchp) { if(sample(c(TRUE, FALSE), 1, prob=c(switchp, 1-switchp))) { rbinom(1, size=n, p=pr); } else { round(runif(1, min=0, max=n)); }}
poll_abc <- replicate(1000000, {
priorp <- runif(1,min=0,max=1)
switch <- 0.5
n1 <- 10
n2 <- 1000
data1 <- data.frame(Yes=simulateHonestPoll(n1, priorp), N=n1)
data2 <- data.frame(Yes=simulateFauxPoll(n2, priorp, switch), N=n2)
newData <- rbind(data1, data2)
if (all(oldData2 == newData)) { return(priorp) }
}
)
resultsABC <- unlist(Filter(function(x) {!is.null(x)}, poll_abc))
summary(resultsABC)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.5256471 0.7427098 0.7584650 0.7860109 0.8133581 0.9765648
hist(resultsABC)
# https://i.imgur.com/atMz0jg.pngThe results are interesting and in this case the summary statistics are misleading: the median is indeed around 75% (as we would expect! since that’s the result of the highly precise poll which has a 50% chance of being the truth) but we see the mean is being pulled away towards the original 90% estimate, and plotting the histogram, bimodality emerges. The posterior reports that there’s still a lot of credibility to the 90% point estimate, but between the original diffuseness of that posterior (leaving a lot of probability to lower responses including, say, 75%) and the high certainty that if accurate the responses will definitely be close to 75%, it winds up peaked at a little higher than 75% (since even if the larger poll is honest, the earlier poll did still find 9⁄10). So it’s not so much that we think the best estimate of true population rate really is 79% (indeed, the mode is more like 75%, but it could easily be far away from 75% and in the 90%s) as we would need to think more about what we want to do with this posterior before we decide how to summarize it.
Mixture
ABC is slow and would not scale to more hypothetical polls unless we abandoned exact ABC inference and began using approximate ABC (entirely possible in this case; instead of strict equality between the original and simulated data, we’d instead accept a sample of p if the simulated dataset’s fractions were within, say, 1% of the originals); and the simulation would need to be rewritten anyway.
MCMC can handle this if we think of our problem as a mixture model: our problem is that we have poll data drawn from two clusters/distributions—one cluster is the true population distribution of opinion, and the other cluster just spits out noise. We have one observation which we know is from first reliable distribution (the 9⁄10 poll result), and one observation which we’re not sure which of the two it came from (750/1000), but we do know that the indexing probability for mixing the two distributions is 50%.
In JAGS, we write down a model in which dcat flips between 1 and 2 if the cluster is not known, specifying which distribution a sample came from and its theta probability, and then we infer the thetas for both distributions. Of course, we only care about the first distribution’s theta since the second one is noise.
library(runjags)
model1 <- "model {
for (i in 1:N) {
y[i] ~ dbinom(theta[i], n[i])
theta[i] <- thetaOfClust[ clust[i] ]
clust[i] ~ dcat(pi[])
}
pi[1] <- switch[1]
pi[2] <- switch[2]
thetaOfClust[1] ~ dbeta(1,1)
thetaOfClust[2] ~ dunif(0,1)
}"
j1 <- autorun.jags(model1, monitor=c("theta"), data = list(N=nrow(oldData2), y=oldData2$Yes, n=oldData2$N, switch=c(0.5, 0.5), clust=c(1,NA))); j1
# ... Lower95 Median Upper95 Mean SD Mode MCerr MC%ofSD SSeff AC.10 psrf
# theta[1] 0.70582 0.75651 0.97263 0.77926 0.07178 --- 0.001442 2 2478 0.12978 1.0011
# theta[2] 0.72446 0.75078 0.77814 0.75054 0.013646 ---0.00009649 0.7 20000 0.009458 1
plot(j1)
# https://i.imgur.com/EaqR0dD.pngSure enough, we get a good match with the ABC estimate: a mean estimate for the population distribution of 78% with a very wide 95% CI and a clearly bimodal distribution with a huge spike at 75%. Since the MCMC mixture model looks completely different from the imperative simulation-based model, the consistency in estimates & distributions gives me some confidence in the results being right.
So we can see how we should update our beliefs—by a perhaps surprising amount towards the unreliable datapoint. The original data was too weak to strongly resist the allure of that highly precise poll.
Weakening Heuristic?
We might try to think of it this way: half the time, the large poll means nothing whatsoever, it contains 0% or no information about the population at all; While the other half of the time, it is exactly what it seems to be and 100% informative; so doesn’t that mean that on average we should treat it as containing half the information we thought it did? And the information is directly based on the sample size: a sample 5x as big contains 5x as much information. So perhaps in this case of all-or-nothing accuracy, we could solve it easily by simply weakening the weight put the unreliable information and shrinking the claimed sample size—instead of treating it as 750 of 1000, treat it as 375⁄500; and if it had been 75,000 of 100,000, convert it to 37,500 of 50,000. This is a simple and intuitive shortcut, but if we think about what the binomial will return as the unreliable poll increases in size or if we look at the results…
switch <- 0.5
oldData3 <- data.frame(Yes=c(9,(750*switch)), N=c(10,(1000*switch)))
b2 <- bayes.binom.test(sum(oldData3$Yes), sum(oldData3$N)); b2
#
# Bayesian First Aid binomial test
#
# data: sum(oldData3$Yes) and sum(oldData3$N)
# number of successes = 384, number of trials = 510
# Estimated relative frequency of success:
# 0.75
# 95% credible interval:
# 0.71 0.79
# The relative frequency of success is more than 0.5 by a probability of >0.999
# and less than 0.5 by a probability of <0.001Unfortunately, this doesn’t work because it doesn’t preserve the bimodal aspect of the posterior, and we get an unimodal distribution ever concentrating on its mean, wiping out the existence of the 0.90 peak. If our untrustworthy poll had instead, say, reported 750,000 out of 1 million, that should only make the peak at 0.75 look like a needle—it should be unable to affect the mass around 0.9, because it doesn’t matter if the data is 100 or 1 million or 1 billion, it still only has a 50% chance of being true. It’s a little hard to see this since the mean frequency of 0.75 is fairly close to the mean of 0.78 from the ABC and we might write this off as approximation error in either the ABC estimate or BFA’s MCMC, but if we look at the 95% CI and note that 0.9 is not inside it or if we plot the posterior (plot(b2)), then the absence of bimodality jumps out. So this trick doesn’t work.
Dysgenics Power Analysis
Current dysgenic estimates predict that genotypic IQ in the West are falling at a substantial rate, amounting to around half a standard deviation or more over the past century, by 1. reducing the frequency at which intelligence-increasing genetic variants occur (through natural selection against such variants) and 2. by increasing the number of new and potentially harmful genetic mutations (increasing mutation load). Estimates are produced indirectly by surveying reproductive rates or by trying to show decreases in phenotypic traits associated with intelligence; it would obviously be preferable to examine dysgenic effects directly, by observing decreases in frequencies or increases in mutation load in a large sample of Western genetic information such as SNP arrays or whole-genomes (respectively). Such direct testing of dysgenics hypotheses are becoming increasingly feasible due to the exponential decrease in SNP & whole-genome sequencing costs creating large datasets (some publicly available) and the recent identification of some intelligence genes. It remains unclear how large these datasets must be to overcome sampling error and yield informative estimates of changes in frequencies or mutation load, however; datasets like PGP or SSGAC may still be too small to investigate dysgenics. I considered the effect size estimates and under some simple models derive power calculations & power simulations of how large a dataset would be required to have an 80% chance of detecting a dysgenic effect: to detect the decrease in intelligence SNPs using SNP data, n≥30,000; to detect the increase in mutation load in whole genomes, n≥160. I then compare to available datasets: the effect on SNPs can be detected by a large number of existing proprietary databases, but there are no public databases which will be large enough in the foreseeable future; the effect on mutation load, on the other hand, can be detected using solely the currently publicly available dataset from PGP. So I conclude that while only the proprietary databases can directly test dysgenic theories of selection for the foreseeable future, there is an opportunity to analyze PGP genomes to directly test the dysgenic theory of mutation load.
The dysgenics hypothesis argues that due to observed reproductive patterns where the highly educated or intelligent tend to have fewer offspring, genotypic IQ (the upper bound on phenotypic IQs set by genes and the sort of thing measured by a polygenic score). If dysgenics is true, then it is an extremely important phenomenon, as important as many things that get far more attention like lead remediation; but to paraphrase Richard Hamming1, just because a problem is important does not mean it is worth working on or researching or discussing if there is no chance of making progress—if the data is hopelessly compromised by many systematic biases which would cause false positives or if the data is too scanty to overcome random error or analyses so flexible that they could deliver any answer the partisan wishes.
Phenotypic data will, in all probability, never allow for a clear & decisive answer to the question of whether dysgenics exists or matters, as long-term comparisons are roughly as credible as noting that global piracy rates have declined while global warming increases, or paracetamol consumption rates have increased in tandem with Alzheimer’s rates; only direct examination of genetics will deliver the decisive answer. It would be nice to have an idea of how much genetic data we would need to overcome random error (and hence, whether it’s possible to make progress in the near future), which we can answer by doing some statistical power analyses.
Changes over time in genetics could be due to changes within a particular race or population (for example, in all white Englishmen), or could be due to population movements like one group replacing or migrating or merging into another (population genetics has revealed innumerable complex examples historically). The latter is possible thanks to the increasing availability of ancient DNA, often made public for researchers; so one could observe very long-term trends with cumulatively large effects (implying that small samples may suffice), but this approach has serious issues in interpretation and questions about how comparable intelligence variants may be across groups or throughout human evolution. With the former, there is less concern about interpretation due to greater temporal and ethnic homogeneity—if a GWAS on white northern Europeans in 201312ya turns up intelligence variants and produces a useful polygenic score, it will almost certainly work on samples of white northern Europeans in 1900125ya too—but because the time-scale is so short the effect will be subtler and harder to detect. Nevertheless, a result within a modern population would be much more credible, so we’ll focus on that.
How subtle and hard to detect an effect are we talking about here? 2012 summarizes a number of estimates:
Early in the 20th century, negative correlations were observed between intelligence and fertility, which were taken to indicate a dysgenic fertility trend (eg. Cattell, 193689ya; Lentz, 192798ya; Maller, 193392ya; Sutherland, 192996ya). Early predictions of the rate of dysgenesis were as high as between 1 and 1.5 IQ points per decade (Cattell, 193788ya, 193689ya)…In their study of the relationship between intelligence and both completed and partially completed fertility, van 1985 reported that the relationships were predominantly negative in cohorts born between the years 1912113ya and 198243ya…Vining (198243ya) was the first to have attempted an estimation of the rate of genotypic IQ decline due to dysgenesis with reference to a large national probability cohort of US women aged between 24 and 34 years in 197847ya. He identified significant negative correlations between fertility and IQ ranging from −.104 to −.221 across categories of sex, age and race, with an estimated genotypic IQ decline of one point a generation. In a 10year follow-up study using the same cohort, Vining (199530ya) re-examined the relationship between IQ and fertility, now that fertility was complete, finding evidence for a genotypic IQ decline of .5 points per generation. 1988 examined the association between fertility and IQ amongst a sample of 9000 Wisconsin high-school graduates (graduated 195768ya). They found a selection differential that would have reduced the phenotypic IQ by .81 points per generation under the assumption of equal IQs for parents and children. With an estimate of .4 for the additive heritability of IQ, they calculated a more modest genotypic decline of approximately .33 points. The study of 1991, which employed the NLSY suggests that once the differential fertility of immigrant groups is taken into consideration, the phenotypic IQ loss amongst the American population may be greater than .8 of a point per generation. Similarly, in summarizing various studies, Herrnstein & Murray (199431ya) suggest that “it would be nearly impossible to make the total [phenotypic IQ decline] come out to less than one point per generation. It might be twice that.” (p. 364). Loehlin (199728ya) found a negative relationship between the fertility of American women aged 35-44 in 199233ya and their educational level. By assigning IQ scores to each of six educational levels, Loehlin estimated a dysgenesis rate of .8 points in one generation. Significant contributions to the study of dysgenesis have been made by Lynn, 199629ya (see also: 201114ya) whose book Dysgenics: Genetic deterioration in modern populations provided the first estimates of the magnitude of dysgenesis in Britain over a 90 year period, putting the phenotypic loss at .069 points per year (about 1.7 points a generation assuming a generational length of 25 years). In the same study, Lynn estimated that the genotypic IQ loss was 1.64 points per generation between 1920105ya and 194085ya, which reduced to .66 points between 195075ya and the present. Subsequent work by Lynn has investigated dysgenesis in other populations. For example Lynn (199926ya) found evidence for dysgenic fertility amongst those surveyed in the 199431ya National Opinion Research Center survey, which encompassed a representative sample of American adults, in the form of negative correlations between the intelligence of adults aged 40+ and the number of children and siblings. Lynn estimates the rate of dysgenesis amongst this cohort at .48 points per generation. In a more recent study, Lynn and van Court (200421ya) estimated that amongst the most recent US cohort for which fertility can be considered complete (ie. those born in the years 1940–9194976ya), IQ has declined by .9 points per generation. At the country level, 2008 have found evidence of a global dysgenesis of around .86 points between 195075ya and 200025ya, which is projected to increase to 1.28 points in the period 2000–502050. This projection includes the assumption that 35% of the variance in cross-country IQ differences is due to the influence of genetic factors. A subsequent study by Meisenberg (200916ya), found that the fertility differential between developed and developing nations has the potential to reduce the phenotypic world population IQ mean by 1.34 points per decade (amounting to a genotypic decline of .47 points per decade assuming Lynn & Harvey’s 35% estimate). This assumes present rates of fertility and pre-reproductive mortality within countries. Meisenberg (201015ya) and 2010 have examined the factors through which intelligence influences reproductive outcomes. They found that amongst the NLSY79 cohort in the United States, the negative correlation between intelligence and fertility is primarily associated with g and is mediated in part by education and income, and to a lesser extent by more “liberal” gender attitudes. From this Meisenberg has suggested that in the absence of migration and with a constant environment, selection has the potential to reduce the average genotypic IQ of the US population by between .4, .8 and 1.2 points per generation.
All of these estimates are genetic selection estimates: indirect estimates inferred from IQ being a heritable trait and then treating it as a natural selection/breeding process, where a trait is selected against based on phenotype and how fast the trait decreases in each succeeding generation depends on how genetic the trait is and how harsh the selection is. So variation in these estimates (quoted estimates per generation range .3–3+) is due to sampling error, differences in populations or time periods, expressing the effect by year or generation, the estimate used for heritability, reliability of IQ estimates, and whether additional genetic effects are taken into account—for example, et al 2015 finds -.262 points per decade from selection, but in another paper argues that paternal mutation load must be affecting intelligence by ~-0.84 in the general population, giving a total of -1 per decade.
Dysgenics effects should be observable by looking at genomes & SNP data with known ages/birth-years and looking for increases in total mutations or decreases in intelligence-causing SNPs, respectively.
Selection on SNPs
Without formally meta-analyzing all dysgenics studies, a good starting point on the selection effect seems like a genetic selection of 1 point per decade or 0.1 points per year or 0.007 standard deviations per year (or 0.7 standard deviations per century).
The most common available genetic data is SNP data, which sequence only the variants most common in the general population; SNP data can look at the effects of genetic selection but will not look at new mutations (since a new mutation would not be common enough to be worth putting onto a SNP chip).
Given a large sample of SNP data, a birth year (or age), and a set of binary SNP variables which cause intelligence (coded as 1 for the good variant, 0 for the others), we could formulate this as a multivariate regression: glm(cbind(SNP1, SNP2, ... SNP_N) ~ Year, family=binomial) and see if the year variable has a negative sign (increasing passage of time predicts lower levels of the good genes); if it does, this is evidence for dysgenics. Better yet, given information about the effect size of the SNPs, we could for each person’s SNP sum the net effects and then regress on a single variable, giving more precision rather than looking for independent effects on each SNP: lm(Polygenic_score ~ Year). Again a negative sign on the year variable is evidence for dysgenics.
Directional predictions are weak, and in this case we have quantitative predictions of how big the effects should be. Most of the public genomes I looked at seem to have the earliest birthdates in the 1950s or so; genomes can come from any age person (parents can give permission, and sequencing has been done prenatally) so the maximum effect is the difference between 195075ya and 2015, which is 65*0.007=0.455 standard deviations (but most genomes will come from intermediate birth-dates, which are less informative about the temporal trend—in the optimal experimental design for measuring a linear trend, half the samples would be from 195075ya and the other half from 2015). If the genetic total is going down by 0.455SDs, how much do the frequencies of all the good genes go down?
One simple model of genotypic IQ would be to treat it as a large number of alleles of equal binary effect: a binomial sum of n = 10,000 1/0 variables with P = 50% (population frequency) is reasonable. (For example, GIANT has found a large number of variants for height, and the GCTAs indicate that SNPs explain much more of variance than the top Rietveld hits currently account for; this specific model is loosely inspired by 2014.) In such a model, the average value of the sum is of course n*p=5000, and the SD is sqrt(n*p*(1-p)) or sqrt(10000*0.5*0.5) or 50. Applying our estimate of dysgenic effect, we would expect the sum to fall by 0.455*50=22.75, so we would be comparing two populations, one with a mean of 5000 and a dysgenic mean of 4977.25. If we were given access to all alleles from a sample of 195075ya and 2015 genomes and so we could construct the sum, how hard would it be able to tell the difference? In this case, the sum is normally distributed as there are more than enough alleles to create normality, so we can just treat this as a two-sample normally-distributed comparison of means (a t-test), and we already have a directional effect size in mind, -0.445SDs, so:
power.t.test(delta=0.455, power=0.8, alternative="one.sided")
# Two-sample t test power calculation
#
# n = 60.4155602
# ...A total n = 120 is doable, but it is unlikely that we will know all intelligence genes anytime soon; instead, we know a few. A new mean of 4977 implies that since total number of alleles is the same but the mean has fallen, the frequencies must also fall and the average frequency falls from 0.5 to 4977.25/10000=0.497725. To go to the other extreme, if we know only a single gene and we want to test a fall from a frequency of 0.50 to 0.4977, we need infeasibly more samples:
power.prop.test(p1=0.5, p2=0.497725, power=0.8, alternative="one.sided")
# Two-sample comparison of proportions power calculation
#
# n = 597,272.2524
# ...1.2m datapoints would be difficult to get, and so a single gene test would be unhelpful; further, a single gene could change frequencies solely through genetic drift without the change being due to dysgenic pressures.
We know a number of genes, though: Rietveld gives 4 good hits, so we can look at a polygenic score from that. They are all of similar effect size and frequency, so we’ll continue under the same assumptions of 1/0 and P = 50%. The non-dysgenic average score is 4*0.5=2, sd=sqrt(4*0.5*0.5)=1. (Naturally, the SD is much larger than before because with so few random variables…) The predicted shift is from frequencies of 0.5 to 0.497, so the dysgenic scores should be 4*0.497=1.988, sd=sqrt(4*0.497*0.503)=0.999. The difference of 0.012 on the reduced polygenic score is d=((2-1.988) / 0.999)=0.012, giving a necessary power of:
power.t.test(delta=0.012006003, power=0.8)
# Two-sample t test power calculation
#
# n = 108904.194
# ...So the 4 hits do reduce the necessary sample size, but it’s still not feasible to require 218k SNP datasets (unless you are 23andMe or SSGAC or an entity like that).
In the current GWAS literature, there are ~9 hits we could use, but the upcoming SSGAC paper promises: “We identified 86 independent SNPs associated with EA (p < 5E-8).”. So how much would 86 improve over 4?
mean old:
86*0.5=43sd old:
sqrt(86*0.5*0.5)=4.6368mean new:
86*0.497=42.742sd new:
sqrt(86*0.497*(1-0.497))=4.6367so d=
(43-42.742)/4.63675=0.0556
power.t.test(delta=((43-42.742)/4.63675), power=0.8)
# Two-sample t test power calculation
#
# n = 5071.166739
# ...So with 75, it drops from 200k to 10.1k.
To work backwards: we know with 1 hit, we need a million SNP datasets (infeasible for any but the largest proprietary databases, who have no interest in studying this hypothesis), and with all hits we need more like 200 genomes (entirely doable with just publicly available datasets like PGP), but how many hits do we need to work with an in-between amount of data like the ~2k genomes with ages I guess may be publicly available now or in the near future?
power.t.test(n=1000, power=0.8)
# Two-sample t test power calculation
#
# n = 1000
# delta = 0.1253508704
hits=437;
mean1=hits*0.5; sd1=sqrt(hits*0.5*0.5);
mean2=hits*0.497; sd2=sqrt(hits*0.497*(1-0.497));
d=(mean1-mean2)/mean(c(sd1,sd2)); d
# [1] 0.1254283986With a polygenic score drawing on 437 hits, then a sample of 2k suffices to detect the maximum decrease.
This is pessimistic because the 10k alleles are not all the same effect size and GWAS studies inherently will tend to find the largest effects first. So the first 4 (or 86) hits are worth the most. The distribution of effects is probably something like an inverse exponential distribution: many small near-zero effects and a few large ones. 2013 released the betas for all SNPs, and the beta estimates can be plotted; each estimate is imprecise and there are artifacts in the beta sizes (SSGAC confirms that they were rounded to 3 decimals), but the distribution looks like a radioactive half-life graph, an inverse exponential distribution. With a mean of 1, we can simulate creating a set of 10k effect sizes which are exponentially distributed and have mean 5000 and SD close to (but larger than) 50 and mimics closely the binomial model:
effects <- sort(rexp(10000)/1, decreasing=TRUE)
genomeOld <- function() { ifelse(sample(c(FALSE,TRUE), prob=c(0.5, 0.5), 10000, replace = TRUE), 0, effects) }
mean(replicate(10000, sum(genomeOld())))
# [1] 5000.270218
sd(replicate(10000, sum(genomeOld())))
# [1] 69.82652816
genomeNew <- function() { ifelse(sample(c(FALSE,TRUE), prob=c(0.497, 1-0.497), 10000, replace = TRUE), 0, effects) }With a dysgenic effect of -0.445SDs, that’s a fall of the sum of random exponentials of ~31, which agrees closely with the difference in polygenic genome scores:
mean(replicate(10000, sum(genomeOld() - genomeNew())))
# [1] 29.75354558For each draw from the old and new populations, we can take the first 4 alleles, which were the ones assigned the largest effects, and build a weak polygenic score and compare means. For example:
polyNew <- replicate(1000, sum(genomeNew()[1:4]))
polyOld <- replicate(1000, sum(genomeOld()[1:4]))
t.test(polyOld, polyNew, alternative="greater")
# Welch Two Sample t-test
#
# data: polyOld and polyNew
# t = 0.12808985, df = 1995.8371, p-value = 0.8980908
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.7044731204 0.8029267301
# sample estimates:
# mean of x mean of y
# 17.72741040 17.67818359Or to mimic 86 hits:
t.test(replicate(1000, sum(genomeOld()[1:86])), replicate(1000, sum(genomeNew()[1:86])))
#
# Welch Two Sample t-test
#
# t = 1.2268929, df = 1997.6307, p-value = 0.2200074
# alternative hypothesis: true difference in means is not equal to 0
# 95% confidence interval:
# -0.8642674547 3.7525210076
# sample estimates:
# mean of x mean of y
# 244.5471658 243.1030390Using the exponential simulation, we can do a parallelized power analysis: simulate draws (i = 300) & tests for a variety of sample sizes to get an idea of what sample size we need to get decent power with 86 hits.
library(ggplot2)
library(parallel) # warning, Windows users
library(plyr)
genomeOld <- function(efft) { ifelse(sample(c(FALSE,TRUE), prob=c(0.5, 0.5), length(efft), replace = TRUE), 0, efft) }
genomeNew <- function(efft) { ifelse(sample(c(FALSE,TRUE), prob=c(0.497, 1-0.497), length(efft), replace = TRUE), 0, efft) }
simulateStudy <- function(n, hits) {
effects <- sort(rexp(10000)/1, decreasing=TRUE)[1:hits]
polyOld <- replicate(n, sum(genomeOld(effects)))
polyNew <- replicate(n, sum(genomeNew(effects)))
t <- t.test(polyOld, polyNew, alternative="greater")
return(data.frame(N=n, P=t$p.value, PO.mean=mean(polyOld), PO.sd=sd(polyOld), PN.mean=mean(polyNew), PN.sd=sd(polyNew))) }
hits <- 86
parallelStudies <- function(n, itr) { ldply(mclapply(1:itr, function(x) { simulateStudy(n, hits); })); }
sampleSizes <- seq(500, 5000, by=100)
iters <- 300
powerExponential <- ldply(lapply(sampleSizes, function(n) { parallelStudies(n, iters) })); summary(powerExponential)
# N P PO.mean PO.sd PN.mean
# Min. : 500 Min. :0.000000000 Min. :222.5525 Min. :23.84966 Min. :221.2894
# 1st Qu.:1600 1st Qu.:0.002991554 1st Qu.:242.8170 1st Qu.:26.46606 1st Qu.:241.3242
# Median :2750 Median :0.023639517 Median :247.2059 Median :27.04467 Median :245.7044
# Mean :2750 Mean :0.093184735 Mean :247.3352 Mean :27.06300 Mean :245.8298
# 3rd Qu.:3900 3rd Qu.:0.107997575 3rd Qu.:251.7787 3rd Qu.:27.64103 3rd Qu.:250.2157
# Max. :5000 Max. :0.997322161 Max. :276.2614 Max. :30.67000 Max. :275.7741
# PN.sd
# Min. :23.04527
# 1st Qu.:26.45508
# Median :27.04299
# Mean :27.05750
# 3rd Qu.:27.63241
# Max. :30.85065
powerExponential$Power <- powerExponential$P<0.05
powers <- aggregate(Power ~ N, mean, data=powerExponential); powers
# 1 500 0.2133333333
# 2 600 0.2833333333
# 3 700 0.2833333333
# 4 800 0.3133333333
# 5 900 0.3033333333
# 6 1000 0.3400000000
# 7 1100 0.4066666667
# 8 1200 0.3833333333
# 9 1300 0.4133333333
# 10 1400 0.4166666667
# 11 1500 0.4700000000
# 12 1600 0.4600000000
# 13 1700 0.4666666667
# 14 1800 0.4733333333
# 15 1900 0.5233333333
# 16 2000 0.5366666667
# 17 2100 0.6000000000
# 18 2200 0.5900000000
# 19 2300 0.5600000000
# 20 2400 0.6066666667
# 21 2500 0.6066666667
# 22 2600 0.6700000000
# 23 2700 0.6566666667
# 24 2800 0.7133333333
# 25 2900 0.7200000000
# 26 3000 0.7300000000
# 27 3100 0.7300000000
# 28 3200 0.7066666667
# 29 3300 0.7433333333
# 30 3400 0.7133333333
# 31 3500 0.7233333333
# 32 3600 0.7200000000
# 33 3700 0.7766666667
# 34 3800 0.7933333333
# 35 3900 0.7700000000
# 36 4000 0.8100000000
# 37 4100 0.7766666667
# 38 4200 0.8000000000
# 39 4300 0.8333333333
# 40 4400 0.8466666667
# 41 4500 0.8700000000
# 42 4600 0.8633333333
# 43 4700 0.8166666667
# 44 4800 0.8366666667
# 45 4900 0.8666666667
# 46 5000 0.8800000000
qplot(N, Power, data=powers) + stat_smooth()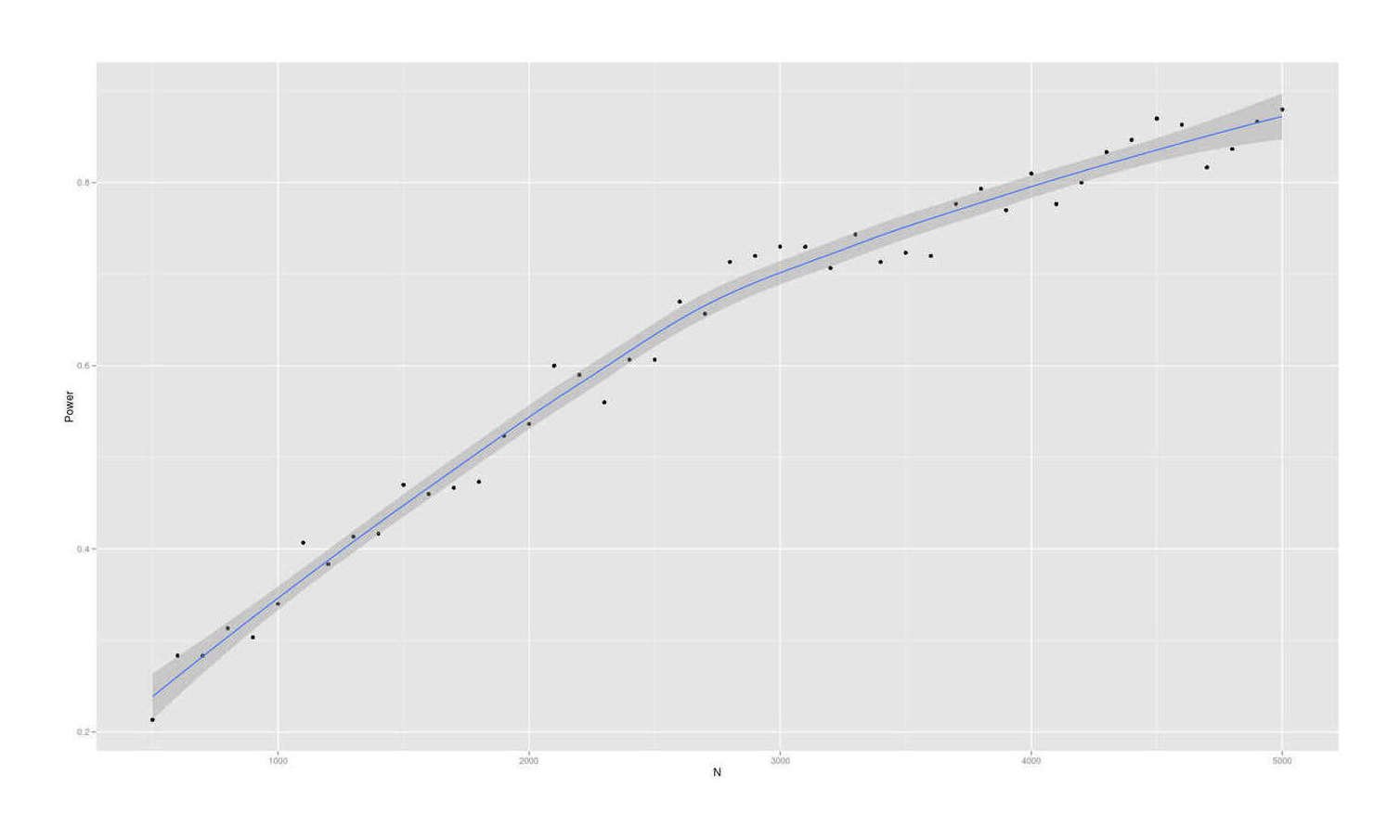
Power for a two-group comparison of old and new SNP datasets for testing a hypothesis of dysgenics
So for a well-powered two-group comparison of 195075ya & 2015 SNP datasets using 86 SNPs, we would want ~4,000 in each group for a total n = 8,000; we do have nontrivial power even at a total n = 1,000 (500 in each group means 21% power) but a non-statistically-significant result will be difficult to interpret and if one wanted to do that, reporting a Bayes factor from a Bayesian hypothesis test would make much more sense to express clearly whether the (non-definitive) data is evidence for or against dysgenics.
This is still too optimistic since we assumed the optimal scenario of only very old and very new genomes, while available genomes are more likely to be distributed fairly uniformly 1950–652015. Per “Optimal design in psychological research”, 1997, we expect a penalty of ~2× in sample size efficiency in going from the optimal two-group extreme endpoints design to samples being uniformly distributed (due to much of our sample size being wasted on estimating small effects) and so we would expect our sample size requirement to at least double to around n = 16,000, but we can do a power simulation here as well. To get the effect size for each year, we simply split the frequency decrease over each year and generate hypothetical genomes with less of a frequency decrease uniformly distributed 1950–652015, and do a linear regression to get a p-value for the year predictor:
hits <- 86
sampleSizes <- seq(8000, 30000, by=1000)
iters <- 100
genome <- function(effects) {
t <- sample(c(1:(2015 - 1950)), 1)
decreasedFrequency <- 0.5 - (((0.5-0.497)/(2015 - 1950)) * t)
geneFlips <- sample(c(FALSE,TRUE), prob=c(decreasedFrequency, 1-decreasedFrequency), replace = TRUE, length(effects))
geneValues <- ifelse(geneFlips, effects, 0)
return(data.frame(Year=1950+t,
PolygenicScore=sum(geneValues)))
}
simulateStudy <- function(n, hits) {
effects <- sort(rexp(10000)/1, decreasing=TRUE)[1:hits]
d <- ldply(replicate(n, genome(effects), simplify=FALSE))
l <- lm(PolygenicScore ~ Year, data=d)
p <- anova(l)$`Pr(>F)`[1]
return(data.frame(N=n, P=p, PO.mean=predict(l, newdata=data.frame(Year=1950)),
PN.mean=predict(l, newdata=data.frame(Year=2015)))) }
parallelStudies <- function(n, itr) { ldply(mclapply(1:itr, function(x) { simulateStudy(n, hits); })); }
powerExponentialDistributed <- ldply(lapply(sampleSizes, function(n) { parallelStudies(n, iters) })); summary(powerExponential)
powerExponentialDistributed$Power <- powerExponentialDistributed$P<0.05
powers <- aggregate(Power ~ N, mean, data=powerExponentialDistributed); powers
# N Power
# 1 8000 0.27
# 2 9000 0.32
# 3 10000 0.35
# 4 11000 0.33
# 5 12000 0.41
# 6 13000 0.34
# 7 14000 0.41
# 8 15000 0.48
# 9 16000 0.55
# 10 17000 0.62
# 11 18000 0.55
# 12 19000 0.60
# 13 20000 0.69
# 14 21000 0.61
# 15 22000 0.65
# 16 23000 0.63
# 17 24000 0.71
# 18 25000 0.67
# 19 26000 0.71
# 20 27000 0.74
# 21 28000 0.70
# 22 29000 0.79
# 23 30000 0.83
qplot(N, Power, data=powers) + stat_smooth()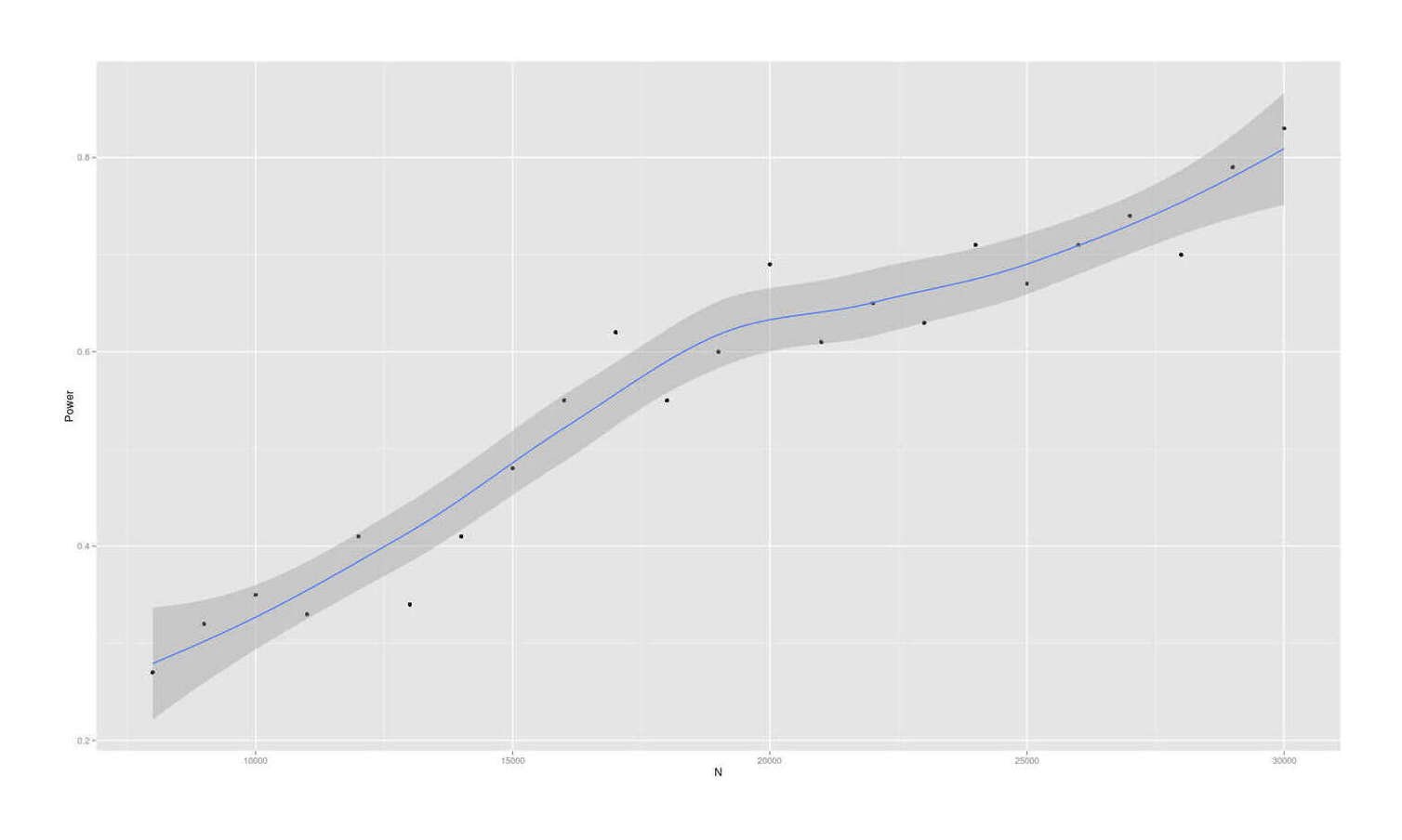
Power to detect dysgenics effect with SNP samples spread over time
In this case, the power simulation suggestions the need for triple rather than double the data, and so a total of n = 30,000 to be well-powered.
Mutation Load
The paternal mutation load should show up as an increase (70 new mutations per generation, 35 years per generation, so ~2 per year on average) over the past century, while the genetic selection will operate by reducing the frequency of variants which increase intelligence. If there are ~70 new mutations per generation and 2 harmful, and there is no longer any purifying selection so that all 70 will tend to remain present, how much does that compare to existing mutation load averages and, more importantly, standard deviations?
A mutation load review leads me to some hard figures from et al 2014 (supplement) using data from et al 2012; particularly relevant is figure 3, the number of single-nucleotide variants per person over the European-American sample, split by estimates of harm from least to most likely: 21345 + 15231 + 5338 + 1682 + 1969 = 45565. The supplementary tables gives a count of all observed SNVs by category, which sum to 300209 + 8355 + 220391 + 7001 + 351265 + 10293 = 897514, so the average frequency must be 45565/897514=0.05, and then the binomial SD will be sqrt(897514*0.05*(1-0.05))=206.47. Considering the two-sample case of 195075ya vs 2015, that’s an increase of 130 total SNVs (65*2), which is 0.63SDs, hence:
power.t.test(d=(130/206), power=0.8)
# Two-sample t test power calculation
#
# n = 40.40035398
# ...A total of n = 80.
This particular set up for the two-sample test can be seen as a linear model with the optimum design of allocating half the sample to each extreme (see again 1997); but more realistically, there is an even distribution across years, in which case the penalty is 2x and n = 160.
Weaknesses
There are some potential problems:
Range restriction: in many IQ-related studies, failure to account for selection effects yielding a limited range of IQs may seriously understate the true correlation; this is true in general but particularly common in IQ studies because selection on IQ (eg. samples of convenience using only college students) is so universal in human society
This may not be such a large issue when dealing with polygenic scores; even severe IQ selection effects will increase polygenic scores only somewhat because the polygenic scores explain so little of IQ variance in the first place.
Self-selection by age: if people providing genetic data are not random samples, then there may be pseudo-trends which can mask a real dysgenic trend or create a pseudo-dysgenic trend where there is none. For example, if young people buying genome or SNP data tend to be above-average in intelligence and scientific interest (which anecdotally they certainly do seem to be), while old people tend to get genomes or SNP data due to health problems (and otherwise have average levels of intelligence and thus polygenic score), then in comparing young vs old, one might find not a dysgenic but a pseudo-eugenic trend instead! Conversely, it could be the other way around, if much fewer elderly get genetic data and younger people are more concerned about future health or are going along with a fad, producing a pseudo-dysgenic effect instead (eg. in the PGP genome data, there seem to be disproportionately more PhDs who are quite elderly, while younger participants are a more scattershot sample from the general population; probably relating to the circumstances of PGP’s founding & Harvard home).
This is probably an issue with databases that rely on voluntary individual contributions, such as PGP, where selection effects have free play. It would be much less of an issue with longitudinal studies where motivations and participation rates will not differ much by age. Since most dysgenic theories accept that recorded IQ scores have remained stable over the 20th century and the decreases in genetic potential either have not manifested yet or have been masked by the Flynn effect & greater familiarity with tests & loss of some g-loading, one might reason that proxies like educational achievement should be increasing throughout one’s sample (since they are known to have increased), and a lack of such a trend indicates selection bias.
Genetic Data Availability
Proprietary
The known proprietary databases have long been large enough to carry out either analysis, as well as countless other analyses (but have failed to and represent a tragedy of the anticommons):
The mutation load analysis requires a whole-genome sample size small enough to have been carried out by innumerable groups post-2009.
For SNPs, an incomplete list of examples of publications based on large samples:
23andMe reached 1 million customers in July 2015, of whom >=80% opt-in to research (>2m as of August 2017, still 80% opt-in, and >6m as of November 2017 with sales increasing); the first questions 23andMe asks all customers are age and education, so they likely have at least 700,000 usable SNPs for both discovering educational associations & dysgenic tests. In June 2010, they claimed to have 29k opt-ins out of 50k customers, implying they were well-powered for a dysgenic test in 201015ya if they had access to a polygenic score, and that in the absence of the score, they could have found the 85 SSGAC hits (using n = 305k) themselves somewhere around mid-2011 or 201213ya and then done a dysgenic test.
the SSGAC collaboration has n = 305k as of late 2015
GIANT: height: n = 253,288
cholesterol: n = 188,000
UK Biobank: n = 152,729 (sequenced/published on as of June 2015; 500k were enrolled and will be covered eventually)
diabetes: n = 114,981
Psychiatric Genomics Consortium: has run multiple studies of varying sizes, the second-largest (a bipolar study) peaking at a total control group of n = 51672, and the largest (schizophrenia) at a control group of n = 113,075
Parkinson’s: n = 100,833 (may overlap with 23andMe and some others)
eczema: n = 95,464
Genetics of Personality Consortium: eg. Neuroticism: n = 63k
Dutch LifeLines Biobank and Cohort: n > 13,000
Health and Retirement Survey: n = 12,500
Swedish TwinGene project: n = 10,682
TwinsUK registry: n = 4,905
Generation Scotland: the Scottish Family Health Study: n = 24,000
The existing private groups do not seem to have any interest in testing dysgenics, with the possible exception of future GWAS studies examining fertility, one of which is mentioned by 2015:
At the time of writing this review, Mills and her research team at the University of Oxford are currently leading a large consortium to engage in the first ever genome-wide association search (GWAS) and meta-analysis of reproductive choice (age at first birth; number of children), conducted in both men and women in over 50 data sets, with the results replicated in additional datasets in a large sample.
The hits in such a GWAS might overlap with intelligence hits, and if the multiple hits increase intelligence but decrease fertility or vice versa (as compared to decreasing or increasing both), that would be evidence for dysgenics. Or, assuming the betas are reported, polygenic scores for fertility and intelligence could be estimated in independent samples and checked for an inverse correlation.
Public
There are a few sources of data, primarily SNP data, which are freely available to all users:
1000 Genomes: unusable due to a deliberate policy decision by 1000 Genomes to delete all phenotype data, including age; similar is 69 Genomes. Both likely would be unusable due to the diversity of the global sample (there is no reason to think that dysgenics pressures are operating in every population at the same strength)
OpenSNP: hosting for user-provided SNP & phenotype data with dumps available; hosts ~2k SNP datasets, but only 270 users have birth-years
SNPedia likewise hosts SNP data (overlapping with OpenSNP) and genome data, but a very small number
Genomes unzipped provides a small amount of data
DNA.LAND: claims n = 8k based on public participation & input (n = 43k as of May 2017), but seems to then restrict access to a small set of researchers
Exome Aggregation Consortium: n = 61,486 exomes; phenotype data is unavailable
Personal Genome Project (PGP): probably the single largest source of open SNP & genome data. ~1252 participants have registered birthdates according to
demographics.tsv, and their statistics page’s graphs indicates <300 whole genomes and <1k SNPs. Phenotype data has been recently released as a SQLite database, making it easier to work with.Genomes: browsing the user lists for ‘Whole genome datasets’, I estimate a total of ~222; looking at the first and last 22 entries, 34 had ages/birth-years, so ~75% of the whole genomes come with the necessary birth-year data, indicating ~166 usable genomes for the purpose of testing dysgenics. With the most recent one uploaded on 2015-10-12, and the earliest recorded being 2011-09-16, that suggests the available genome number increases by ~0.25/day. 166 is uncomfortably close to the requirement for a well-powered test, and there may not be enough data to account for glitches in the data or allow for more complicated statistical testing, but if we wanted to double the available data, we’d only need to wait around 885 days or 2.5 years (or less, depending on whether the collapse in genome sequencing prices continue and prices drop below even the current $1k genomes).
SNPs: PGP has ~656 23andMe SNP datasets (the number of SNP datasets sourced from other providers is quite small so I didn’t include them), dated 2015-10-21–2011-01-06, so assuming same birth-date percentage, 0.37 per day. Unfortunately, to get 30k SNP datasets through PGP, we would have to wait (linearly extrapolating) 291 years. (Making matters worse, in October 2015, 23andMe doubled its price and reduced the quality of SNP coverage, which will discourage many users and push other users to purchase whole-genome sequencing instead.)
Power Analysis for Racial Admixture Studies of Continuous Variables
I consider power analysis of a genomic racial admixture study for detecting genetic group differences affecting a continuous trait such as IQ in US African-Americans, where ancestry is directly measured by genome sequencing and the comparisons are all within-family to eliminate confounding by population structure or racism/colorism/discrimination. The necessary sample size for well-powered studies is closely related to the average size of differences in ancestry percentage between siblings, as the upper bound on IQ effect per percentage is small, requiring large differences in ancestry to detect easily. A within-family comparison of siblings, due to the relatively small differences in ancestry between siblings estimated from IBD measurements of siblings, might require n > 50,000 pairs of siblings to detect possible effects on IQ, an infeasible sample size. An alternative design focuses on increasing the available ancestry differences within a family unit by comparing adoptees with siblings; the larger within-population standard deviation of ancestry creates larger & more easily-detected IQ differences. A random-effects meta-analysis of past admixture & ancestry studies suggests the SD in heterogeneous samples may range from 2% to 20% with a mean of 11% (95% predictive interval), yielding sample sizes of n > 20,000, n = 1100, and n = 500. Hence, an adoption study is probably in the feasible range, with required sample sizes comparable to annual adoption rates among US African-Americans.
Admixture studies examine racial phenotypic differences in traits such as blood pressure by comparing people with ancestry from multiple groups, and correlating differences in ancestry percentage with differences in the phenotype. So, for example, African-Americans have higher blood-pressure than white Americans, and most African-Americans have an average white ancestry of something like 20-25% (see later); if having 26% white ancestry predicts slightly lower blood pressure while 24% predicts higher, that suggests the difference is (as is currently believed) genetic; and this logic can be used to narrow down to specific chromosome regions, and has contributed to study of racial differences in disease.
One application would be to thorny questions like potential group differences in non-medical traits like intelligence. The standard admixture design, requiring a few thousand subjects spanning the full range, might not necessarily work here here because of the claimed environmental effects. A proposed resolution to the question is to do an admixture study comparing African-American siblings. Siblings are highly genetically related on average (50%) but in a randomized fashion due to recombination; so two siblings, including fraternal twins, born to the same parents in the same family in the same neighborhood going to the same schools, will nevertheless have many different variants, and will differ in how related they are—the average is 50% but it could be as low as 45% or high as 55%. So given two siblings, they will differ slightly in their white ancestry, and if indeed white ancestry brings with it more intelligence variants, then the sibling with a higher whiter percentage ought to be slightly more intelligent on average, and this effect will have to be causal, as the inheritance is randomized and all other factors are equal by design. (A result using ancestry percentages measured in the general population, outside families, would be able to make far more powerful comparisons by comparing people with ~0% white ancestry to those with anywhere up to 100%, and require small sample sizes, and such analyses have been done with the expected result, but are ambiguous & totally unconvincing, as the correlation of greater whiteness with intelligence could easily be due to greater SES or greater blackness could be a marker for recent immigration or any of a number of confounds that exist.) This has historically been difficult or impossible since how does one measure the actual ancestry in siblings? But with the rise of cheap genotyping, precise measure of actual (rather than average) ancestry can be done for <$100, so that is no longer an obstacle.
Sibling Power Analysis
How many sibling pairs would this require?
you are trying to regress
IQ_difference ~ Ancestry_differencethe SD of the IQ difference of siblings is known—it’s ~13 IQ points (nonshared environment + differences in genetics)
of this, a small fraction will be explained by the small difference in ancestry percentage
the power will be determined by the ratio of the sibling SD to the IQ-difference-due-to-ancestry-difference SD, giving an effect size, which combined with the usual alpha=0.05 and beta=0.80, uniquely determines the sample size
IQ-difference-due-to-ancestry-difference SD will be the advantage of better ancestry times how much ancestry differs
if you knew the number of relevant alleles, you could calculate through the binomial the expected SD of sibling ancestor differences. As there are so many alleles, it will be almost exactly normal. So it’s not surprising that siblings overall, for all variants, are 50% IBD with a SD of 4%.
If we treated it as simply as possible, et al 2006 for an analogous height analysis says they measured 588 markers. So a binomial with 588 draws and p = 0.5 implies that 147 markers are expected to be the same:
588 * 0.5*(1-0.5)
# [1] 147and the distribution around 147 is 12, which is ~8%:
sqrt((588 * 0.5*(1-0.5)))
# [1] 12.12435565
12/147
# [1] 0.08163265306Visscher does a more complicated analysis taking into account closeness of the markers and gets a SD of 3.9%: equation 7; variance = 1/(16*L) - (1/3*L^2), where L = 35, so
L=35; sqrt(1/(16*L) - (1/(3*L^2)))
# [1] 0.03890508247And 2011’s theoretical modeling gives an expected sibling SD of SD of 3.92%/3.84% (Table 2), which are nearly identical. So whatever the mean admixture is, I suppose it’ll have a similar SD of 4-8% of itself.
IIRC, African-Americans are ~25% admixed, so with a mean admixture of 25%, we would expect siblings differences to be or 1% difference.
If that 75% missing white ancestry accounts for 9 IQ points or 0.6SDs, then each percentage of white ancestry would be 0.6/75 =0.008 SDs.
So that SD of 1% more white ancestry yields an SD of 0.008 IQ, which is superimposed on the full sibling difference of 0.866, giving a standardized effect size/d of 0.008 / 0.866 = 0.0092
Let me try a power simulation:
n <- 10000
siblings <- data.frame(
sibling1AncestryPercentage = rnorm(n, mean=25, sd=1),
sibling1NonancestryIQ = rnorm(n, mean=0, sd=12),
sibling2AncestryPercentage = rnorm(n, mean=25, sd=1),
sibling2NonancestryIQ = rnorm(n, mean=0, sd=12))
siblings$sibling1TotalIQ <- with(siblings, sibling1NonancestryIQ + sibling1AncestryPercentage*(0.008*15))
siblings$sibling2TotalIQ <- with(siblings, sibling2NonancestryIQ + sibling2AncestryPercentage*(0.008*15))
siblings$siblingAncestryDifference <- with(siblings, sibling1AncestryPercentage - sibling2AncestryPercentage)
siblings$siblingIQDifference <- with(siblings, sibling1TotalIQ - sibling2TotalIQ )
summary(siblings)
# ...
# siblingAncestryDifference siblingIQDifference
# Min. :-5.370128122 Min. :-68.2971343
# 1st Qu.:-0.932086950 1st Qu.:-11.7903864
# Median : 0.002384529 Median : -0.2501536
# Mean : 0.007831583 Mean : -0.4166863
# 3rd Qu.: 0.938513265 3rd Qu.: 11.0720667
# Max. : 5.271052675 Max. : 67.5569825
summary(lm(siblingIQDifference ~ siblingAncestryDifference, data=siblings))
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -0.4192761 0.1705125 -2.45892 0.0139525
# siblingAncestryDifference 0.3306871 0.1220813 2.70874 0.0067653
#
# Residual standard error: 17.05098 on 9998 degrees of freedom
# Multiple R-squared: 0.000733338, Adjusted R-squared: 0.0006333913
# F-statistic: 7.337294 on 1 and 9998 DF, p-value: 0.006765343
confint(lm(siblingIQDifference ~ siblingAncestryDifference, data=siblings))
# 2.5 % 97.5 %
# (Intercept) -0.75351500523 -0.08503724643
# siblingAncestryDifference 0.09138308561 0.56999105507
admixtureTest <- function(n, alpha=0.05, ancestryEffect=0.008) {
siblings <- data.frame(
sibling1AncestryPercentage =pmax(0, rnorm(n, mean=25, sd=1)),
sibling1NonancestryIQ = rnorm(n, mean=0, sd=12),
sibling2AncestryPercentage = pmax(0,rnorm(n, mean=25, sd=1)),
sibling2NonancestryIQ = rnorm(n, mean=0, sd=12))
siblings$sibling1TotalIQ <- with(siblings, sibling1NonancestryIQ + sibling1AncestryPercentage*(ancestryEffect*15))
siblings$sibling2TotalIQ <- with(siblings, sibling2NonancestryIQ + sibling2AncestryPercentage*(ancestryEffect*15))
siblings$siblingAncestryDifference <- with(siblings, sibling1AncestryPercentage - sibling2AncestryPercentage)
siblings$siblingIQDifference <- with(siblings, sibling1TotalIQ - sibling2TotalIQ )
p <- summary(lm(siblingIQDifference ~ siblingAncestryDifference, data=siblings))$coefficients[8]
return(p<alpha)
}
power <- function(n, iters=10000, n.parallel=8) {
library(parallel)
library(plyr)
mean(unlist(mclapply(1:n.parallel, function(i) {
replicate(iters/n.parallel, admixtureTest(n)) }))) }
# powers <- sapply(seq(100, 10000, by=10), power)
power(100)
# [1] 0.0502
power(500)
# [1] 0.0535
power(1500)
# [1] 0.0642
power(15000)
# [1] 0.2251
power(50000)
# [1] 0.6077So the estimated sample size is extremely large, well into the scores of thousands. This is large enough that it will be some time before biobanks or population samples are well-powered: participants may not have siblings, those siblings may be included, only ~15% of the American population is AA, all participants must be sequenced, imperfect reliability of measurements can greatly increase the necessary sample size, and so on. If it requires n = 70,000, half of participants have a matching sibling, and it’s drawn proportionally from the general population, that would imply that a total sample size of almost 1m. (For comparison, that’s about twice the size of the UK Biobank, and the US Precision Medicine Initiative cohort program aims for 1m total participants by 2020.)
Simplifications aside, it is difficult to see any way to bring this method down into the low thousands range, as that would require siblings to vary tremendously more in ancestry, have much more homogeneous IQs than they do, or ancestry to be vastly more potent than it could possibly be.
Adoption Power Analysis
One possibility would be to examine a different population, perhaps one with more African ancestry and thus larger between-sibling ancestry differences and effects, such as Brazil; but that would raise questions about relevance to the USA. So another possibility is to drop the idea of using only biological siblings. Is there any way to have ancestry differences as large as in the general population, but within a family? Half-siblings come to mind but those more typically tend to join the household as older kids or teenagers, so aren’t so good. One possibility is adoptees: there are a substantial number of African-American children adopted into other African-American households (white parents adopting black children is controversial and rarer, described as “decreasing dramatically”, but still substantial in total numbers, at least 20,000), and even a noticeable number of African children adopted abroad (14,800 from Ethiopia just 1999–15201411ya, with more adoption from Nigeria & the Congo). The same logic of the within-family study should apply but to unrelated siblings who will have far greater differences in ancestry now (possibly anywhere up to 50% if an African child is adopted into an African-American family with considerable white ancestry & some luck). This would increase power dramatically, perhaps enough to bring the study within the realm of near-future feasibility.
Examining adoptions of African children would not be a convincing way of establishing group differences, particularly for IQ, as there are many known environmental harms (eg. pre-natal lack of iodine is known to cause large impairments in cognitive which cannot be repaired later in life, and poor iodization is frequent in Africa), so while examining African adoptees would doubtless require a very small sample size, the results would be uninterpretable. So the more interesting case is instead examining AA adoptees/siblings, all of whom are raised in a wealthy (and iodine-sufficient) industrialized country.
In this case, we’re considering a pair of an AA sibling with the same IQ & ancestry distributions, as compared with adoptees who are either African (100% African ancestry) or likewise have the same IQ/ancestry distributions. Since the sibling & adoptee are unrelated, they effectively vary & differ as much as two random people from the general population would in IQ & African ancestry, except for shared-environment effects on IQ; shared-environment for adult IQ is relatively low, maybe 10% of variance. So instead of an SD of 15, they would vary moderately less, like 14.23 points (sqrt(15^2 * 0.9)).
One assumption here is a shared mean: one would actually expect, given the association of lighter skin with higher wealth/SES and darker with lower wealth/SES, that the adopting parents (and hence their biological children) would be relatively high on European ancestry, and conversely, the mothers giving up children for adoption would be relatively low, so the expected difference in ancestry is higher than simulated. Assuming equal means, however, is a conservative assumption since if such a correlation holds, the differences will be larger, hence the ancestry effect sizes larger, hence smaller sample sizes required. In the extreme version of this, the adoptive family is white and so the ancestry difference is maximal (~99% vs ~20%), requiring even smaller sample sizes, but at the cost of introducing complications like whether there are interactions with the white adoptive family not present in an AA adoptive family; in any case, such trans-racial adoption is apparently unpopular now, so it may not come up much.
Mean Population European Ancestry & Population Standard Deviation
Ancestry effects remain as before; the mean ancestry is not too important as long as it’s not near 0, but since adoptees are drawn from the general population, the ancestry SD must be adjusted but it’s unclear what the right SD here is—cited studies range from 4% up to 11%, and this is a key parameter for power (with 4%, then sibling and adoptee will tend to be quite similar on ancestry percentage & much more data will be required, but with 11% they will differ a good deal and make results stronger).
Reported figures from the genetics literature for European ancestry in US African-American range from 14% to 24%, reflecting both sampling error and various biases & self-selection & geographic/regional effects in the datasets:
et al 2008, “A Panel of Ancestry Informative Markers for Estimating Individual Biogeographical Ancestry and Admixture From Four Continents: Utility and Applications”: 14.3%, SD 13.3% (n = 136)
et al 2009, “Association of Substance Use Disorders With Childhood Trauma but not African Genetic Heritage in an African American Cohort”: 7%, SD 9% (n = 864); this is a little odd since they allocate the 21% non-African ancestry (African ancestry: 079%, SD 14%) to Europe, Middle East, Central Asia, Native American, East Asia, and Oceania, but it’s hard to imagine that really corresponds to the ancestry of New Jersey African-Americans; if we ignore that attempt at splitting the non-African ancestry, 21% & SD 14% might be more consistent.
et al 2009, “Genetic ancestry, social classification, and racial inequalities in blood pressure in Southeastern Puerto Rico”: European ancestry isn’t reported and Puerto Ricans have too much other ancestry to simply subtract the reported African ancestries
et al 2010, “Blood vitamin D levels in relation to genetic estimation of African ancestry”, Table 1: mean African ancestry of 92.9% implies European ancestry ~7.1%, ~IQR of African ancestry implies SD ~8%, (n = 379)
et al 2010, “Genome-wide patterns of population structure and admixture in West Africans and African Americans”: median 18.5%, 25th-75th percentiles: 11.6-27.7%; no mean or SD reported in the paper or supplemental materials I could find, but the median/percentiles suggest an SD of ~4.65% (
qnorm(0.25) * (0.116 - 0.185); n = 365)et al 2012, “Relationship between Adiposity and Admixture in African American and Hispanic American Women”: 22.5%, SD 14.7% (n = 11712)
Henry Louis Gates Jr summarizes results available to him in February 201312ya: 29%, 22%, 19%, 19% (unspecified sample sizes & population SDs)
According to Ancestry.com, the average African American is 65% sub-Saharan African, 29% European and 2% Native American.
According to 23andme.com, the average African American is 75% sub-Saharan African, 22% European and only 0.6% Native American.
According to Family Tree DNA.com, the average African American is 72.95% sub-Saharan African, 22.83% European and 1.7% Native American.
According to National Geographic’s Genographic Project, the average African American is 80% sub-Saharan African, 19% European and 1% Native American.
According to AfricanDNA, in which I am a partner with Family Tree DNA, the average African American is 79% sub-Saharan African, 19% European and 2% Native American.
et al 2014, “The Genetic Ancestry of African Americans, Latinos, and European Americans across the United States”: mean 24%, SD not reported, and Bryc declined to provide any information about the study & population SD when contacted but pixel-counting Figure S1/Figure S18 yields the mean of 24% and an SD of ~17% (n = 5269)
et al 2016, “The Great Migration and African-American Genomic Diversity”: reports 3 cohorts with European ancestry at:
SCCS: 14(13.65-14.43)% (n = 2128)
HRS: 16.7(16.16-17.27)% (n = 1501524ya)
ASW: 21.3(19.50-23.20)% (n = 97)
but no population SDs, with statistically-significant differences likely due to recruiting:
The overall proportion of African ancestry is substantially higher in the SCCS and HRS than in the ASW and the recently published 23andMe cohort [12] (Table 1). The HRS cohort can be thought of as representative of the entire African-American population, while the SCCS focuses primarily on individuals attending community health centers in rural, underserved locations in the South. By contrast, the sampling for the ASW and 23andMe did not aim for specific representativeness, and the ascertainment in the 23andMe cohort might have enriched for individuals with elevated European ancestry (see Materials and Methods and discussion in [12]). In the HRS, average African ancestry proportion is 83% in the South and lower in the North (80%, bootstrap p= 6 × 10−6) and West (79%, p= 10−4) (Fig 1). Within the SCCS, African ancestry proportion is highest in Florida (89%) and South Carolina (88%) and lowest in Louisiana (75%) with all three significantly different from the mean (Florida p = 0.006, South Carolina p = 4 × 10−4, and Louisiana p< 10−5; bootstrap). The elevated African ancestry proportion in Florida and South Carolina is also observed in the HRS and in the 23andMe study [12], but Louisiana is more variable across cohorts (Fig 1E). As expected, European ancestry proportions largely complement those of African ancestry across the US.
et al 2016, “Biogeographic ancestry, cognitive ability, and socioeconomic outcomes”’s supplementary information: 17%, SD 11% (n = 140)
Considering just studies with usable ancestry percentages, population SD, and n, and using inferred SDs from Signorello:
admixture <- read.csv(stdin(), header=TRUE, colClasses=c("factor", "numeric", "numeric", "integer"))
Study,Mean,SD,N
"Halder et al 2008",0.143,0.133,136
"Ducci et al 2009",0.07,0.09,864
"Signorello et al 2010",0.071,0.08,379
"Bryc et al 2010",0.185,0.0465,365
"Nassir et al 2012",0.225,0.147,11712
"Bryc et al 2014",0.24,0.17,5269
"Kirkegaard et al 2016",0.17,0.11,140
# what is the standard error/precision of a population SD? http://davidmlane.com/hyperstat/A19196.html
admixture$SD.SE <- (0.71*admixture$SD) / sqrt(admixture$N)
summary(admixture)
# Study Mean SD N SD.SE
# Bryc et al 2010 :1 Min. :0.0700000 Min. :0.0465000 Min. : 136.0 Min. :0.0009644066
# Bryc et al 2014 :1 1st Qu.:0.1070000 1st Qu.:0.0850000 1st Qu.: 252.5 1st Qu.:0.0016954481
# Ducci et al 2009 :1 Median :0.1700000 Median :0.1100000 Median : 379.0 Median :0.0021739221
# Halder et al 2008 :1 Mean :0.1577143 Mean :0.1109286 Mean : 2695.0 Mean :0.0034492579
# Kirkegaard et al 2016:1 3rd Qu.:0.2050000 3rd Qu.:0.1400000 3rd Qu.: 3066.5 3rd Qu.:0.0047591374
# Nassir et al 2012 :1 Max. :0.2400000 Max. :0.1700000 Max. :11712.0 Max. :0.0080973057
# Signorello et al 2010:1
library(metafor)
r.mean <- rma(yi=Mean, sei=SD/sqrt(N), measure="SMD", ni=N, data=admixture); r.mean
# Random-Effects Model (k = 7; tau^2 estimator: REML)
#
# tau^2 (estimated amount of total heterogeneity): 0.0046 (SE = 0.0027)
# tau (square root of estimated tau^2 value): 0.0680
# I^2 (total heterogeneity / total variability): 99.82%
# H^2 (total variability / sampling variability): 566.51
#
# Test for Heterogeneity:
# Q(df = 6) = 3477.2614, p-val < .0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# 0.1578 0.0258 6.1187 <.0001 0.1072 0.2083
predict(r.mean)
# pred se ci.lb ci.ub cr.lb cr.ub
# 0.1578 0.0258 0.1072 0.2083 0.0153 0.3003
r.sd <- rma(yi=SD, sei=SD.SE, measure="SMD", ni=N, data=admixture); r.sd
# Random-Effects Model (k = 7; tau^2 estimator: REML)
#
# tau^2 (estimated amount of total heterogeneity): 0.0018 (SE = 0.0011)
# tau (square root of estimated tau^2 value): 0.0425
# I^2 (total heterogeneity / total variability): 99.77%
# H^2 (total variability / sampling variability): 440.67
#
# Test for Heterogeneity:
# Q(df = 6) = 3819.2793, p-val < .0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# 0.1108 0.0162 6.8587 <.0001 0.0792 0.1425
predict(r.sd)
# pred se ci.lb ci.ub cr.lb cr.ub
# 0.1108 0.0162 0.0792 0.1425 0.0216 0.2001
par(mfrow=c(2,1))
forest(r.mean, slab=admixture$Study)
forest(r.sd, slab=admixture$Study)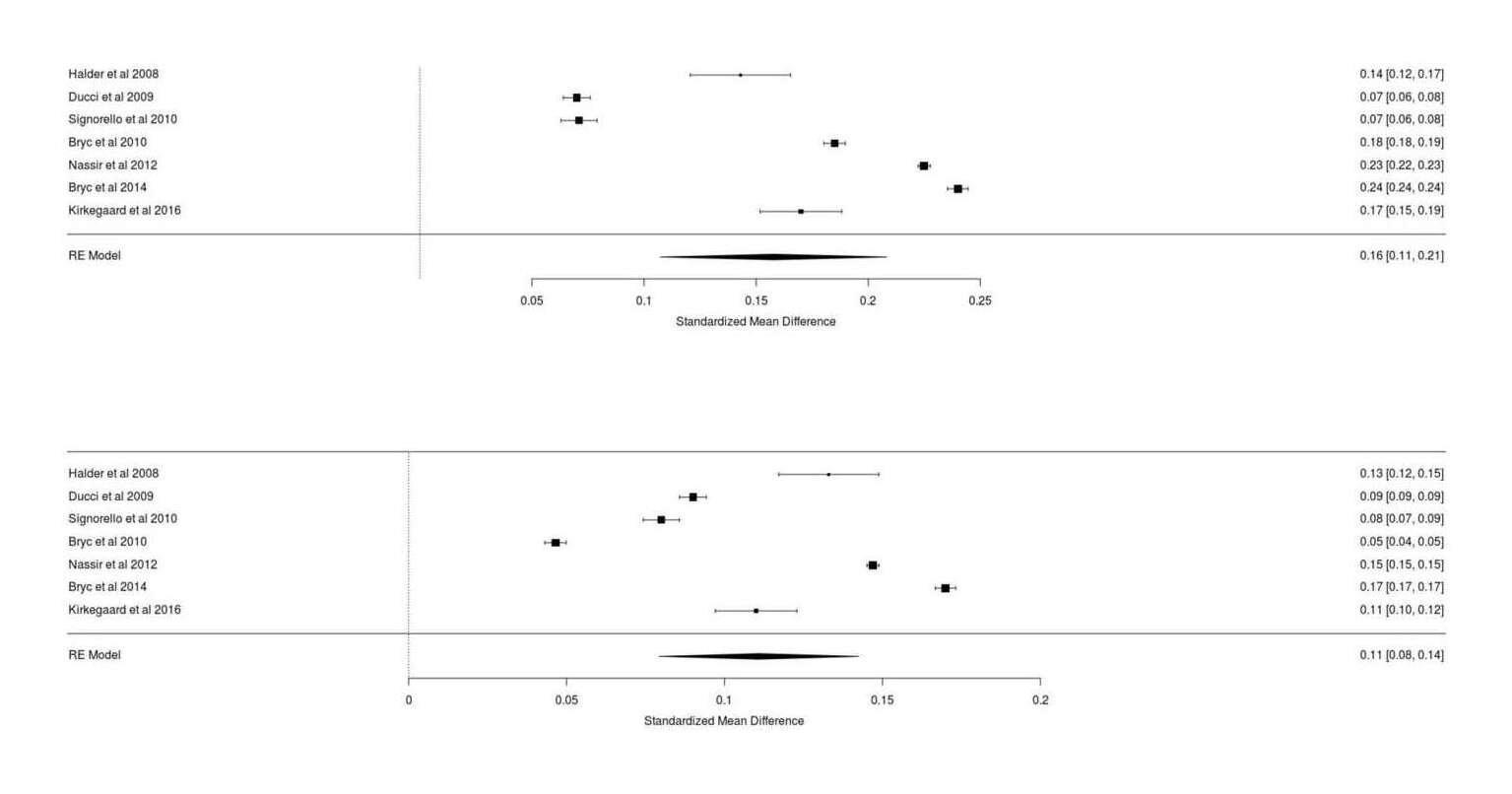
Meta-analytic summary of US African-American’s mean European ancestry percentage & population SD of that percentage
There is high heterogeneity, as expected, and the meta-analytic summary are consistent with simply taking the mean, so meta-analysis was not really necessary.
The issue of heterogeneity depends on how one wants to interpret these numbers: as the true latent African-American population mean/SD of European ancestry, or as a way to estimate the possible spread of sampling? In the former, the heterogeneity is a serious issue because it suggests the estimate may be badly biased or at least is highly imprecise; in the latter, it is both a curse and a benefit, since it implies that it is possible to recruit for genetics studies samples with a wide range of ancestry (thereby greatly increasing statistical power) but also that one might get unlucky & wind up with a very ancestry-homogeneous sample (if the sample turns out to have an SD as high as 20%, excellent; if it’s as low as 7.9%, one is in trouble).
So for power analysis one might check the meta-analytic mean case, as well as the prediction interval (a 95% CI around the SD/mean does not mean that 95% of the true effects, including the inherent heterogeneity, will fall in that interval): SDs of 2%, 11%, and 20%. (For any cost-benefit analysis or trying to optimize expenditures, one would want to work with the posterior distributions to average over everything, but for just general informative purposes, those 3 are good parameters to check.)
Power Simulation
Code:
adopteeTest <- function(n, alpha=0.05, ancestryEffect=0.008, populationAncestryMean=0.1440, populationAncestrySD=0.1008, c=0.1) {
unrelatedSiblingSD <- sqrt(15^2 * (1-c)) # subtract 10% for same shared-environment
siblings <- data.frame(
sibling1AncestryPercentage = pmax(0, rnorm(n, mean=populationAncestryMean*100, sd=populationAncestrySD*100)),
sibling1NonancestryIQ = rnorm(n, mean=0, sd=unrelatedSiblingSD),
adopteeAncestryPercentage = pmax(0, rnorm(n, mean=populationAncestryMean*100, sd=populationAncestrySD*100)),
adopteeNonancestryIQ = rnorm(n, mean=0, sd=unrelatedSiblingSD))
siblings$sibling1TotalIQ <- with(siblings, sibling1NonancestryIQ + sibling1AncestryPercentage*(ancestryEffect*15))
siblings$adopteeTotalIQ <- with(siblings, adopteeNonancestryIQ + adopteeAncestryPercentage*(ancestryEffect*15))
siblings$siblingAncestryDifference <- with(siblings, sibling1AncestryPercentage - adopteeAncestryPercentage)
siblings$siblingIQDifference <- with(siblings, sibling1TotalIQ - adopteeTotalIQ )
p <- summary(lm(siblingIQDifference ~ siblingAncestryDifference, data=siblings))$coefficients[8]
return(p<alpha)
}
power <- function(n, sd, iters=10000, n.parallel=8) {
library(parallel)
library(plyr)
mean(unlist(mclapply(1:n.parallel, function(i) {
replicate(iters/n.parallel, adopteeTest(n, populationAncestrySD=sd)) }))) }
ns <- seq(100, 10000, by=100)
powerLow <- sapply(ns, function(n) { power(n, sd=0.0216)})
powerMean <- sapply(ns, function(n) { power(n, sd=0.1108)})
powerHigh <- sapply(ns, function(n) { power(n, sd=0.2001)})
library(ggplot2); library(gridExtra)
pl <- qplot(ns, powerLow) + coord_cartesian(ylim = c(0,1))
pm <- qplot(ns, powerMean) + coord_cartesian(ylim = c(0,1))
ph <- qplot(ns, powerHigh) + coord_cartesian(ylim = c(0,1))
grid.arrange(pl, pm, ph, ncol=1)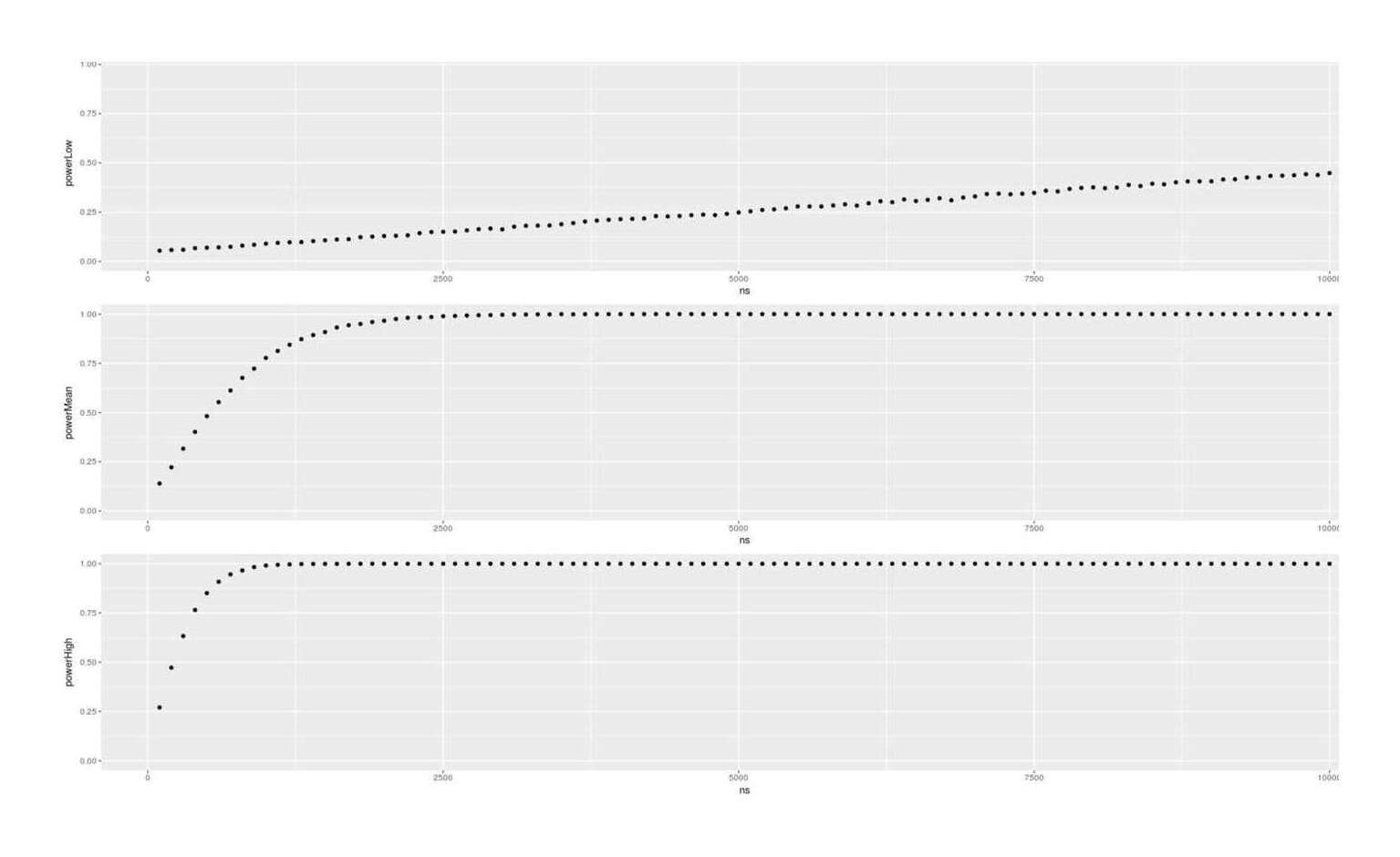
Power analysis for detecting European ancestry on IQ in an adoptee family study with predicted low/mean/high population variance in ancestry percentage (higher variance=larger statistical power=fewer samples required)
So for the worst-case SD, sample size is unclear but n > 20,000 pairs; mean SD, n = 1100 pairs; high SD, n = 500 pairs. The latter two are feasible amounts for population registries or adoption-focused cohort studies. Thus genome adoption studies, combined with the much less powerful but more common within-sibling comparisons, are capable of delivering precise answers to long-standing questions about the origins of group differences with moderate sample sizes.
Operating on an Aneurysm
In the excellent neurosurgery memoir Do No Harm: Stories of Life, Death, and Brain Surgery (Henry Marsh 201411ya), chapter 2 “Aneurysm”, there is a passage on weighing the costs of action and inaction:
“A thirty-two-year-old woman,” he said tersely. “For surgery today. Had some headaches and had a brain scan.” As he talked a brain scan flashed up on the wall.
…“It’s an unruptured aneurysm, seven millimetres in size,” Fiona—the most experienced of the registrars—said. “So there’s a point zero five per cent risk of rupture per year according to the international study published in 199827ya.” “And if it ruptures?” “Fifteen per cent of people die immediately and another thirty per cent die within the next few weeks, usually from a further bleed and then there’s a compound interest rate of four per cent per year.”
…If we did nothing the patient might eventually suffer a haemorrhage which would probably cause a catastrophic stroke or kill her. But then she might die years away from something else without the aneurysm ever having burst. She was perfectly well at the moment, the headaches for which she had had the scan were irrelevant and had got better. The aneurysm had been discovered by chance. If I operated I could cause a stroke and wreck her—the risk of that would probably be about four or five per cent. So the acute risk of operating was roughly similar to the life-time risk of doing nothing. Yet if we did nothing she would have to live with the knowledge that the aneurysm was sitting there in her brain and might kill her any moment.
Reading this, I was a little surprised by Marsh’s evaluation given those specific numbers. Intuitively, it did not seem to me that a single risk of 5% was anywhere near as bad as a lifelong risk of 0.5%, for a 32 year old woman who would probably live another 50 years—the one number is 10x bigger than the other, but the other number is 50x bigger, and a quick heuristic for the total probability of many independent small probabilities is to just sum them up, suggesting that the risk of the untreated aneurysm was much worse (50*0.005=0.25, and 0.25>0.05). So I thought after I finished reading the book, I would work it out a little more accurately.
Risk
Specifically, this is a 32yo woman and the UK female life expectancy is ~80yo in 2015, so she had ~48 years left. The consequences of the aneurysm bursting is a large chance of instant death or else severe disability with death to soon follow; the consequence of surgery going wrong is also instant death or severe disability, presumably with a high chance of death soon following, so it looks like we can assume that the bad outcome in either case is the same. what is the probability of the aneurysm never bursting in all 48 years? (1-0.005)^48 = 0.786, or a probability of bursting of 21%. 21% is 4x larger than 5%. Since 21% is 4x larger and the consequences are similar, this would suggest that the risks are not “roughly similar” and it looks much worse to not operate.
Expected Loss
But that’s just the risk of an event, not the expected loss:
In the case of doing surgery immediately, the expected loss, with years treated equally and a 5% instant risk from operation, is simply
48 * 0.005 = 0.24years of life; all 48 years are risked on a single throw of the surgical dice, but after that she is safe.In the case of doing nothing and letting the aneurysm stay with a 0.5% annual risk from non-operation, it’s not as simple as
48 * 0.21 = 10.1years, because you cannot die of an aneurysm if you died in a previous year. The risk will instead follow a negative binomial distribution (number of years until 1 failure), and then the loss is the 48 years minus however many she actually got. That’s not the same as the expectation of the negative binomial, which in this case is 200 years (the expectation of a negative binomial with 1 failure and a success rate of 1-0.005 is1/(1-(1-0.005))=200) and she will die of other causes before then, in which case the aneurysm turned out to be harmless.We can simulate many draws from the negative binomial, ignore as 0 any time where the aneurysm struck after her life expectancy of 48 more years is past, hold onto the losses, and calculate the mean loss:
mean(sapply(rnbinom(10e4, 1, 0.005), function(years) { if(years>48) { 0; } else { 48-years; }}))→ 5.43.
So the expected loss from surgery looks even better than the risk did, as it is 22.6x smaller.
QALY/DALY Adjustment
What about adjusting for older years being less valuable? We might say that the surgery look unfairly good because we are ignoring how its losses are front-loaded in the 30s, some of the best years of one’s life, and treating a loss of her 33rd year as being as bad as a loss of her 48th year. In terms of age weighting, DALYs usually use a 3% annual discounting; DALYs and QALYs differ in some ways but for this analysis I think we can treat them as equivalent and use the DALY age-discounting to calculate our QALYs. So we can redo the two expected losses including the discounting to get:
Surgery:
0.05 * sum((1-0.03)^(0:48))→ 1.291No surgery:
mean(unlist(sapply(sapply(rnbinom(10e4, 1, 0.005), function(years) { if(years>48) { 0; } else { 48-years; }}), function(yr) { sum((1-0.03)^(0:yr)); })))→ 4.415
By appropriately penalizing the surgery’s loss of high-quality early years as compared to the aneurysm’s loss of just some elderly years, the surgery’s superiority falls to 3.4x, and the gain is 3.124. (And if we include the mental wellbeing of the woman as a final touch, the surgery looks even better.)
How sensitive is the surgical superiority to the parameters?
Surgical risk: a 4x increase in risk to 20% would create parity
Aneurysm risk: if the annual risk of aneurysm were as low as 0.04% rather than 0.5%, then there would be parity
Life expectancy & discount rate: no change will reverse the ordering
It seems extremely unlikely that Marsh could be as wrong about the surgical risk as to mistake 5% for 20%, especially for an operation he says he used to do routinely, and it also seems unlikely that the study on the annual risk of an aneurysm bursting could be as far off as 10x, so the difference is solid.
Cost-Benefit
Finally, having a surgery is much more expensive than not having it. Surgery is always expensive, and neurosurgery undoubtedly so—elsewhere in the book, Marsh quotes an American neurosurgeon’s estimate of $100,000 for a particularly complex case. Clipping an aneurysm surely cannot cost that much (being both much simpler and also being done in a more efficient healthcare system), but it’s still not going to be trivial. Does the cost of aneurysm surgery outweigh the benefit?
To convert the DALY loss to a dollar loss, we could note that UK PPP per capita is ~$38,160 (2013) so the gain from surgery would be (4.415 - 1.291) * 38169=$119k, well above the $100k worst-case. Or more directly, the UK NHS prefers to pay <£20,000 per QALY and will generally reject treatments which cost >£30,000 per QALY as of 20072 (implying QALYs are worth somewhat less than £30,000); the median US 2008 hospital cost for clipping an aneurysm is $36,188 or ~£23,500; and the gain is 3.124 QALYs for ~£7500/QALY—so clipping the aneurysm in this case definitely clears the cost-benefit threshold (as we could have guessed from the fact that in the anecdote, the NHS allows her to have the surgery).
After calculating the loss of years, differing values of years, and cost of surgery, the surgery still comes out as substantially better than not operating.
The Power of Twins: Revisiting Student’s Scottish Milk Experiment Example
MCTS
An implementation in R of a simple Monte Carlo tree search algorithm (using Thompson sampling rather than a UCT) implemented with data.tree. This MCTS assumes binary win/loss (1/0) terminal rewards with no intermediate rewards/costs so it cannot be used to solve general MDPs, and does not expand leaf nodes in the move tree passed to it. (I also suspect parts of it are implemented wrong though it reaches the right answer in a simple Blockworld problem and seems OK in a Tic-Tac-Toe problem. I have since understood how memoization works with backwards induction and would probably probably drop the painful explicit tree manipulation in favor of the indirect recursive aproach.)
library(data.tree)
## MCTS helper functions:
playOutMoves <- function(move, state, actions) {
for (i in 1:length(actions)) {
state <- move(state, actions[i])$State
}
return(state)
}
playOutRandom <- function(move, state, actions, timeout=1000, verbose=FALSE) {
action <- sample(actions, 1)
turn <- move(state, action)
if(verbose) { print(turn); };
if (turn$End || timeout==0) { return(turn$Reward) } else {
playOutRandom(move, turn$State, actions, timeout=timeout-1, verbose) }
}
createTree <- function(plys, move, moves, initialState, tree=NULL) {
if (is.null(tree)) { tree <- Node$new("MCTS", win=0, loss=0) }
if (plys != 0) {
for(i in 1:length(moves)) {
x <- tree$AddChild(moves[i], win=0, loss=0)
createTree(plys-1, move, moves, initialState, tree=x)
}
}
# cache the state at each leaf node so we don't have to recompute each move as we later walk the tree to do a rollout
tree$Do(function(node) { p <- node$path; node$state <- playOutMoves(move, initialState, p[2:length(p)]); }, filterFun = isLeaf)
return(tree)
}
mcts <- function (tree, randomSimulation, rollouts=1000) {
replicate(rollouts, {
# Update posterior sample for each node based on current statistics and use Thompson sampling.
# With a beta uniform prior (Beta(1,1)), update on binomial (win/loss) is conjugate with simple closed form posterior: Beta(1+win, 1+n-win).
# So we sample directly from that posterior distribution for Thompson sampling
tree$Do(function(node) { node$Thompson <- rbeta(1, 1+node$win, 1+(node$win+node$loss)-node$win) })
# find & run 1 sample:
node <- treeWalk(tree)
rollout <- randomSimulation(node$state)
if(rollout==1) { node$win <- node$win+1; } else { node$loss <- node$loss+1; }
# propagate the new leaf results back up tree towards root:
tree$Do(function(x) { x$win <- Aggregate(x, "win", sum); x$loss <- Aggregate(x, "loss", sum) }, traversal = "post-order")
})
}
## walk the game tree by picking the branch with highest Thompson sample down to the leaves
## and return the leaf for a rollout
treeWalk <- function(node) {
if(length(node$children)==0) { return(node); } else {
children <- node$children
best <- which.max(sapply(children, function(n) { n$Thompson; } ))
treeWalk(children[[best]]) } }
mctsDisplayTree <- function(tree) {
tree$Do(function(node) { node$P <- node$win / (node$win + node$loss) } )
tree$Sort("P", decreasing=TRUE)
print(tree, "win", "loss", "P", "Thompson")
}
## Blockworld simulation
## 0=empty space, 1=agent, 2=block, 3=goal point
blockActions <- c("up", "down", "left", "right")
blockInitialState <- matrix(ncol=5, nrow=5, byrow=TRUE,
data=c(0,0,0,0,1,
0,2,0,0,2,
0,0,0,2,0,
0,2,0,0,0,
0,0,0,0,3))
blockMove <- function(state, direction) {
if(state[5,5] == 2) { return(list(State=state, Reward=1, End=TRUE)) }
position <- which(state == 1, arr.ind=TRUE)
row <- position[1]; col <- position[2]
rowNew <- 0; colNew <- 0
switch(direction,
# if we are at an edge, no change
up = if(row == 1) { rowNew<-row; colNew<-col; } else { rowNew <- row-1; colNew <- col; },
down = if(row == 5) { rowNew<-row; colNew<-col; } else { rowNew <- row+1; colNew <- col; },
left = if(col == 1) { rowNew<-row; colNew<-col; } else { rowNew <- row; colNew <- col-1; },
right = if(col == 5) { rowNew<-row; colNew<-col; } else { rowNew <- row; colNew <- col+1; }
)
# if there is not a block at the new position, make the move
if (state[rowNew,colNew] != 2) {
state[row,col] <- 0
state[rowNew,colNew] <- 1
return(list(State=state, Reward=0, End=FALSE))
} else {
state[rowNew,colNew] <- 1
state[row,col] <- 0
switch(direction,
# if the block is at the edge it can't move
up = if(rowNew == 1) { } else { state[rowNew-1,colNew] <- 2 },
down = if(rowNew == 5) { } else { state[rowNew+1,colNew] <- 2 },
left = if(colNew == 1) { } else { state[rowNew,colNew-1] <- 2 },
right = if(colNew == 5) { } else { state[rowNew,colNew+1] <- 2 } )
# a block on the magic 5,5 point means a reward and reset of the playing field
if(state[5,5] == 2) { return(list(State=state, Reward=1, End=TRUE)) } else { return(list(State=state, Reward=0, End=FALSE)) }
}
}
## Blockworld examples:
# blockMove(blockInitialState, "left")
# blockMove(blockInitialState, "down")
# blockMove(blockInitialState, "right")$State
# blockMove(blockMove(blockInitialState, "right")$State, "down")
# blockMove(blockMove(blockMove(blockInitialState, "down")$State, "down")$State, "down")
# playOutMoves(blockMove, blockInitialState, c("down", "down", "down"))
# playOutRandom(blockMove, blockInitialState, blockActions)
tree <- createTree(2, blockMove, blockActions, blockInitialState)
mcts(tree, function(state) { playOutRandom(blockMove, state, blockActions) })
mctsDisplayTree(tree)
tree2 <- createTree(3, blockMove, blockActions, blockInitialState)
mcts(tree2, function(state) { playOutRandom(blockMove, state, blockActions) })
mctsDisplayTree(tree2)
## Tic-Tac-Toe
tttActions <- 1:9
tttInitialState <- matrix(ncol=3, nrow=3, byrow=TRUE, data=0)
tttMove <- function(state, move) {
move <- as.integer(move)
# whose move is this? Player 1 moves first, so if the number of pieces are equal, it must be 1's turn:
player <- 0; if(sum(state == 1) == sum(state == 2)) { player <- 1 } else { player <- 2}
# check move is valid:
if(state[move] == 0) { state[move] <- player }
## enumerate all possible end-states (rows, columns, diagonals): victory, or the board is full and it's a tie
victory <- any(c(
all(state[,1] == player),
all(state[1,] == player),
all(state[,2] == player),
all(state[2,] == player),
all(state[,3] == player),
all(state[3,] == player),
all(as.logical(c(state[1,1], state[2,2], state[3,3]) == player)),
all(as.logical(c(state[1,3], state[2,3], state[3,1]) == player))
))
tie <- all(state != 0)
# if someone has won and the winner is player 1, then a reward of 1
if(victory) { return(list(State=state, Reward=as.integer(player==1), End=TRUE)) } else {
if(tie) { return(list(State=state, Reward=0, End=TRUE)) } else {
return(list(State=state, Reward=0, End=FALSE)) }
}
}
## Tic-Tac-Toe examples:
# tttMove(tttMove(tttMove(tttInitialState, 5)$State, 9)$State, 2)
# playOutMoves(tttMove, tttInitialState, c(5, 9, 2))
# playOutRandom(tttMove, tttInitialState, tttActions, verbose=TRUE)
treeTTT <- createTree(2, tttMove, tttActions, tttInitialState)
mcts(treeTTT, function(state) { playOutRandom(tttMove, state, tttActions) })
mctsDisplayTree(treeTTT)
## hypothetical: if opponent plays center (5), what should be the reply?
treeTTT2 <- createTree(2, tttMove, tttActions, tttMove(tttInitialState, 5)$State)
mcts(treeTTT2, function(state) { playOutRandom(tttMove, state, tttActions) })
mctsDisplayTree(treeTTT2)Candy Japan A/B Test
DeFries-Fulker Power Analysis
DeFries-Fulker (DF) extremes analysis
et al 1987, “Evidence for a genetic aetiology in reading disability of twins” /doc/genetics/heritable/1987-defries-2.pdf
“A Model-Fitting Implementation of the DeFries-Fulker Model for Selected Twin Data” 2003 /doc/genetics/heritable/2003-purcell.pdf
et al 1991, “Colorado Reading Project: An update”
2006 “A Finite Mixture Model for Genotype and Environment Interactions: Detecting Latent Population Heterogeneity” https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.534.6298&rep=rep1&type=pdf
et al 2001, “Comorbidity between verbal and non-verbal cognitive delays in 2-year-olds: A bivariate twin analysis”
https://www.sciencedirect.com/science/article/pii/S0160289614001676 “Thinking positively: The genetics of high intelligence”, et al 2015
2017, “An Investigation of Genetic and Environmental Influences Across The Distribution of Self-Control”
generateSiblingPair <- function(ID=TRUE) {
## Population mean 100, SD 15; let's make family means distributed normally too;
## heritability 0.8, shared environment 0.1, siblings share half of genes on average + shared environment
## so a pair of siblings has 1 - (0.8*0.5+0.1) = 0.5 of the variance of the general population.
parental <- mean(rnorm(1,mean=100,sd=15*0.8), rnorm(1,mean=100,sd=15*0.8))
siblings <- rnorm(2, mean=parental, sd=15*(1 - (0.8*0.5+0.1)))
## Siblings will tend to vary this much, unless they are, lamentably, one of the, say,
## 5% struck by mutational lightning and reduced to an IQ of, let's say, 80
if(ID) { siblings <- ifelse(rbinom(2,1,prob=0.05), siblings,rnorm(2, mean=80, sd=15)) }
return(c(max(siblings), min(siblings)))
}
generateSiblingPairs <- function(n,ID=TRUE) { as.data.frame(t(replicate(n, generateSiblingPair(ID=ID)))) }
## dataset with lightning:
df <- round(rescale(generateSiblingPairs(1000000, ID=TRUE), mean=5, sd=2))
## floor/ceiling at 0/9 for everyone:
df[df$V1>9,]$V1 <- 9
df[df$V1<1,]$V1 <- 1
df[df$V2>9,]$V2 <- 9
df[df$V2<1,]$V2 <- 1
## dataset without:
df2 <- round(rescale(generateSiblingPairs(1000000, ID=FALSE), mean=5, sd=2))
df2[df2$V1>9,]$V1 <- 9
df2[df2$V1<1,]$V1 <- 1
df2[df2$V2>9,]$V2 <- 9
df2[df2$V2<1,]$V2 <- 1
par(mfrow=c(2,1))
hist(df$V1 - df$V2)
hist(df2$V1 - df2$V2)
## mixture modeling:
library(flexmix)
## check k=1 vs k=2 on df1, where k=2 is ground truth:
g1.1 <- flexmix(I(V1-V2) ~ 1, k=1, data=df)
g1.2 <- flexmix(I(V1-V2) ~ 1, k=2, data=df)
summary(g1.1); summary(g1.2)
## check k=1 vs k=2 on df2, where k=1 is ground truth:
g2.1 <- flexmix(I(V1-V2) ~ 1, k=1, data=df2)
g2.2 <- flexmix(I(V1-V2) ~ 1, k=2, data=df2)
summary(g2.1); summary(g2.2)Inferring Mean IQs From SMPY/TIP Elite Samples
Samples taken from the extremes of mixtures of distributions can have very different properties than random samples, such as the tail effect of wildly disproportionate representation of one distribution due to order statistics/threshold selection.
This can be used to infer differing means.
I demonstrate working backwards from the racial composition of SMPY/TIP samples of extremely (1-in-10,000) gifted youth to estimate the overall racial means, which is consistent with the known racial means and hence an unbiased selection process, using ABC to infer Bayesian credible intervals on the estimated means.
The properties of statistical distributions can be very different from the properties of specific subsets of those distributions in counterintuitive ways. A point drawn from an extreme will exhibit “regression to the mean”, a phenomenon which routinely trips people up. Another common example is that a small difference in means for many distributions can lead to large differences in extreme subsets.
For example, male and female average heights differ by a relatively small amount, inches at most. So in a random sample, plenty of women will be taller than men, and vice versa. However, if instead ask the sex of the tallest person in the sample, it will often be male, and the larger the sample, the more certain we can be that it will be male, and that the top X% by height will be male. Likewise, if we wanted to start a basketball league and recruited the tallest 100 people in the country, this small mean difference will show up as our entire basketball league turning out to be male. (And since height is highly heritable, we may find out that many of them are related!) What seemed like a small difference become a large one; we could have worked it out in advance if we had thought about it.
Reasoning from the general to the particular turned out to be tricky in this case because we were dealing with extreme values rather than random samples—1 basketball player chosen by height from thousands of people. Many things of great interest turn out to be like that: we are interested in the extremes much more than the expectation. Running a 2-hour marathon is an extreme on athleticism; winning the Nobel is an extreme on scientific accomplishment; being enlisted in the NBA is an extreme on height; being admitted to MIT/Stanford/Harvard is an extreme on intelligence; murdering someone is an extreme on violence; winning an Academy Award is an extreme on acting success. When we ask questions like, “why does the world record in this sport keep being shattered” or “why are so many NBA players related” or “how good can we expect the best chess player to be in 10 years” or “does this racial composition prove bias” or “how much more important are the best authors in literature than obscurer figures” or “why do so few women win the Field Medal”, we’re asking extreme value questions whose answers may be counterintuitive—and the answer may be as simple as the shape of distributions, and a slightly lower mean here or a slightly higher standard deviation there. (Working backwards from a sample selected for passing a threshold to a mean can be called “the method of limits” or “the method of thresholds”.)
The study “When Lightning Strikes Twice: Profoundly Gifted, Profoundly Accomplished”, et al 2016 describes the accomplishments of the Duke TIP sample, 259 children selected for their intelligence by taking the highest-scorers out of 425,000 adolescents taking the SAT (usually <13yo) starting in 198144ya, representing the top 0.01% of the test-takers. The TIP sample parallels the better-known SMPY sample, which also selected extremely intelligent adolescents, who were included in a longitudinal sample. It’s frequently suggested, based on anecdotal evidence or some biased convenience samples, that more intelligence may not be better; extremely intelligent people may be unhealthy, neurotic, insane, isolated, lonely, discriminated against by society and their peers, and doomed to failure; or if things are not quite that dire, as all studies show things improving up to 130, then at around that point greater intelligence may stop making any difference, and there be little difference between someone with an IQ of 130 and 160. This is difficult to study cross-sectionally, because once you start talking about as extreme as 0.01%, it is difficult to recruit any subjects at all, and your sample will be biased in unknown ways; if you only look at successful people, you are missing the hypothetical homeless bum living out of a trash can who is a troubled and misunderstood genius. To solve these problems, you want to filter through hundreds of thousands of people so you can select the very brightest possible, and you want to find them as early as possible in life, before they have had any chance to fail or succeed, and track them longitudinally as they grow up. This is what the SMPY & TIP studies do, and the results are that the subjects are spectacularly successful in life; great intelligence is not harmful and the returns to greater intelligence are not zero even as high as 1 in 10,000.
et al 2016 also reports the ethnic breakdown of the TIP and SMPY samples: 72% white, 22% Asian, 6% not reported or other. This distribution might seem remarkable given that subjects taking the SAT in 198144ya were born ~1970, when the USA was ~77% white, ~11% black, and ~0.7% Asian, so white are slightly under-represented, blacks are very under-represented (even if we assume all 6% are black, then that’s still half), and Asians are 31x (!) overrepresented.
## SMPY/TIP sample size & ethnic percentages: https://pbs.twimg.com/media/Cj9DXwxWEAEaQYk.jpg
tip <- 259; smpy <- 320 ## total: 579
white <- ((0.65*tip) + (0.78*smpy)) / (tip+smpy)
asian <- ((0.24*tip) + (0.20*smpy)) / (tip+smpy)
white; asian
# [1] 0.7218480138
# [1] 0.2178929188
# https://drjamesthompson.blogspot.com/2016/06/some-characteristics-of-eminent-persons.html
# > The data on ethnicity are rather sparse, but we can do a little bit of work on them by looking at US Census
# > figures for the 1970s when most of these children were born: White 178,119,221...Asia 1,526,401...So, in the
# > absence of more detailed particulars about the Other category, Asians win the race by a country mile. If we
# > simplify things by considering only Whites, Blacks and Asians the US in 1970 then the country at that time was
# > 88% White, 11% Black, and less than 1% Asian. The actual results of eminent students are 77% White, 0% Black,
# > 22% Asian. No need for a Chi square.
#
# Asian is 0.7%: 1526401 / (178119221 / 0.80)
whiteRR <- white / 0.77; asianRR <- asian / 0.007
whiteRR; asianRR
# [1] 0.937464953
# [1] 31.12755983Of course, races in the USA have long differed by mean intelligence, with the rule of thumb being Asians ~105 IQ, whites ~100, and blacks ~90. So the order is expected—but still, 31x! Are the results being driven by some sort of pro-Asian bias or otherwise bizarre?
But this is an extreme sample. 1-in-10,000 is far out on the tails: 3.71SDs.
-qnorm(1/10000)
# [1] 3.719016485Maybe this is normal. Can we work backwards from the overrepresentations to what differences would have generated them?
Yes, we can, even with this small sample which is so extreme and unrepresentative of the general population. This is because it is an order statistics problem: we know the order represented by the sample and so can work back to parameters of the distribution the order statistics are being generated by. Since IQ is a normal distribution, we know the overrepresentation RR, and the exact cutoff/limit used in the sample, we can convert the limit to a standard deviations, and then find the normal distribution which is RR (31) times the normal distribution at a standard deviations.
We can compare using two pnorms and shifting the second by a SDs. So for example, shifting by 15 IQ points or 1 SD would lead to 84x overrepresentation
pnorm(qnorm(1/10000)) / pnorm(qnorm(1/10000) - (15/15))
# [1] 84.39259519We would like to solve for the shift which leads to an exact overrepresentation like 31.127; an optimization routine like R’s optim function can do that, but it requires an error to minimize, so minimizing pnorm()/pnorm(x) doesn’t work since it just leads to negative infinity, nor will RR == pnorm()/pnorm(x) work, because it evaluates to 0 for all values of x except the exact right one . Instead, we minimize the squared error between the ratio predicted by a particular x and our observed RR. This works:
## An optimization routine which automatically finds for us the IQ increase which most closely matches the RR:
solver <- function(RR, cutoff=10000) {
optim(1,
function(IQ_gain) { (RR - (pnorm(qnorm(1/cutoff)) / pnorm(qnorm(1/cutoff)-(IQ_gain/15))))^2 },
)$par }
100 + solver(whiteRR)
# [1] 99.75488281
100 + solver(asianRR)
# [1] 111.8929688So our inferred white & Asian populations means are: 99.8 and 111.9. These are relatively close to the expected values.
This approach can be used to infer other things as well. For example, the SMPY/TIP papers have not, as far as I’ve seen, mentioned what fraction of the white subjects were ethnic Jewish; since they are so over-represented in areas like Nobel prizes, we would expect many of the SMPY/TIP white students to have been Jewish. Using an estimate of the Jewish population in 197055ya and estimates of their mean IQ, we can work forward to what fraction of SMPY/TIP subjects might be Jewish. The 1970–197154ya National Jewish Population Study estimated “5,800,000 persons (of whom 5,370,000 were Jews) living in Jewish households” out of a total US population of 205 million, or 2.8% of the total population or ~3.6% of the white population. So of the ~418 white subjects, ~15 would be expected to be Jewish under the null hypothesis of no difference. The majority of American Jews are of Ashkenazi descent3, for whom intelligence estimates are debated but tend to range 105-115 (with occasional samples suggesting even higher values, like 1957). In the 1964 Ohio sample (IQ ~143), 8% were Jewish4; in Terman’s (ratio IQ >140) 1920s sample in SF/LA, 10% were Jewish; 1930s sample (>180) turned up 51⁄55 or 90% Jewish5; 1936’s 193194ya Wisconsin state sample found 18% of the Jewish sample to be in the top decile vs 10% American; in the Hunter College Elementary School sample 1948–12196065ya (>140, mean 157) in New York City, 62% were Jewish ( et al 1989, et al 19936). Given estimates of the Jewish population of children in those specific times and places, one could work backwards to estimate a Jewish mean.
We can calculate the fraction of the white sample being Jewish for each possible mean IQ:
proportion <- function (gain, cutoff=10000) {
(pnorm(qnorm(1/cutoff)) / pnorm(qnorm(1/cutoff)-(gain/15))) }
possibleIQs <- seq(5, 15, by=0.5)
data.frame(Advantage=possibleIQs, Fraction.of.white=(sapply(possibleIQs, proportion) * 15) / 418)
Advantage Fraction.of.white
1 5.0 0.1415427303
2 5.5 0.1633099334
3 6.0 0.1886246225
4 6.5 0.2180947374
5 7.0 0.2524371552
6 7.5 0.2924980125
7 8.0 0.3392769622
8 8.5 0.3939561508
9 9.0 0.4579348680
10 9.5 0.5328710150
11 10.0 0.6207307813
12 10.5 0.7238482059
13 11.0 0.8449966589
14 11.5 0.9874747049
15 12.0 1.1552093388
16 12.5 1.3528802227
17 13.0 1.5860693342
18 13.5 1.8614413902
19 14.0 2.1869615788
20 14.5 2.5721585555
21 15.0 3.0284424112Judging from earlier samples with high cutoffs, I’d guess SMPY/TIP has at least a majority Jewish, giving a mean IQ of ~110; this is similar to estimates based on regular samples & estimation. This result is also similar to La Griffe du 2003 threshold analysis estimating a mean IQ of 112 based on Ashkenazi overrepresentation among USSR championship chess players, 111 based on Western Fields Medal awards, and 110 based on the USA/Canada Putnam competition. But if the mean IQ was as high as 112, then almost every single white subject would be Jewish in every sampling, which seems implausible and like something so striking that anyone writing or involved with SMPY/TIP would have to have mentioned at some point—right?
For the same reason, the original estimate of 112 for the Asians strikes me as on the high side. This could be due to problems in the data like underestimating the Asian population at the time—perhaps the Southeast/Midwest states that TIP samples from were more than 0.7% Asian—or it could be due to sampling error (only n = 579, after all).
Working backwards doesn’t immediately provide any measurement of precision or confidence intervals. Presumably someone has worked out analytic formulas which come with standard errors and confidence intervals, but I don’t know it. Instead, since the selection process which generated our data is straightforward (population mean → millions of samples → take top 1-in-10000s → calculate overrepresentation), I can again use Approximate Bayesian computation (ABC) to turn a simulation of the data generating process into a method of Bayesian inference on the unknown parameters (population means) and get credible intervals.
What sort of confidence do we have in these estimates given that these RRs are based only on? We can simulate SMPY/TIP-like selection by taking the hypothetical means of the two groups, generating ~3 million simulates (579 * 10000) each, selecting the top 1/10,000th7, taking the RRs and then solving for the mean IQ. If we provide a prior on the means and we hold onto only the means which successfully generate SMPY/TIP-like fractions of 72% & 21%, this becomes ABC with the saved means forming the posterior distribution of means. (It would likely be faster to use MCMC like JAGS, but while JAGS provides truncated normal distributions which one could sample from quickly, and the necessary pnorm/qnorm functions, but it’s not clear to me how one could go about estimating the overperformance ratio and the binomial.8) For my priors, I believe that the rule of thumbs of 100⁄105 are accurate and highly unlikely to be more than a few points off, so I use a very weak prior of populations means being .
In exact ABC, we would keep only data which exactly matched 72%/22%, but that would require rejecting an extremely large number of samples. Here we’ll loosen it to ±2% tolerance:
simulateTIPSMPY <- function() {
## informative priors: IQs are somewhere close to where we would estimate based on other datasets
whiteMean <- round(rnorm(1, mean=100, sd=5), digits=2)
asianMean <- round(rnorm(1, mean=105, sd=5), digits=2)
iqCutoff <- 100 + -qnorm(1/10000) * 15
whites <- rnorm(0.770 * 579 * 10000, mean=whiteMean, sd=15)
whiteSample <- max(1, sum(ifelse(whites>iqCutoff, 1, 0)))
asians <- rnorm(0.007 * 579 * 10000, mean=asianMean, sd=15)
asianSample <- max(1, sum(ifelse(asians>iqCutoff, 1, 0)))
## white+Asian = 92% of original total sample, so inflate by that much to preserve proportions: 1.08
totalSample <- (whiteSample+asianSample) * (1 + (1-(white+asian)))
whiteFraction <- round(whiteSample / totalSample, digits=2)
asianFraction <- round(asianSample / totalSample, digits=2)
# print(paste("samples: ", c(whiteSample, asianSample), "fractions: ", c(whiteFraction, asianFraction)))
tolerance <- 0.02
if ((abs(whiteFraction - 0.7218480138) < tolerance) && (abs(asianFraction - 0.2178929188) < tolerance)) {
return(data.frame(White=whiteMean, Asian=asianMean))
}
}
library(parallel); library(plyr)
simulateSamples <- function(n.sample=10000, iters=getOption("mc.cores")) {
## because of rejection sampling, no run is guaranteed to produce a sample so we loop:
results <- data.frame()
while (nrow(results) < n.sample) {
simResults <- ldply(mclapply(1:iters, function(i) { simulateTIPSMPY() } ))
results <- rbind(results, simResults)
# print(paste("Samples so far: ", nrow(results)))
}
return(results) }
posteriorSamples <- simulateSamples()
mean(posteriorSamples$White < posteriorSamples$Asian)
# [1] 1
## we have relatively few samples, so get a better posterior estimate by shuffling the posterior samples & comparing many times:
mean(replicate(1000, mean(c(sample(posteriorSamples$White) < sample(posteriorSamples$Asian)))))
# [1] 0.9968822
quantile(probs=c(0.025, 0.975), posteriorSamples$White, na.rm=TRUE)
# 2.5% 97.5%
# 89.49975 101.38050
quantile(probs=c(0.025, 0.975), posteriorSamples$Asian, na.rm=TRUE)
# 2.5% 97.5%
# 101.37000 116.74075
par(mfrow=c(2,1))
hist(posteriorSamples$White, main="Posterior white mean IQ estimated from SMPY/TIP cutoff & ratio", xlab="IQ")
hist(posteriorSamples$Asian, main="Posterior Asian mean", xlab="IQ")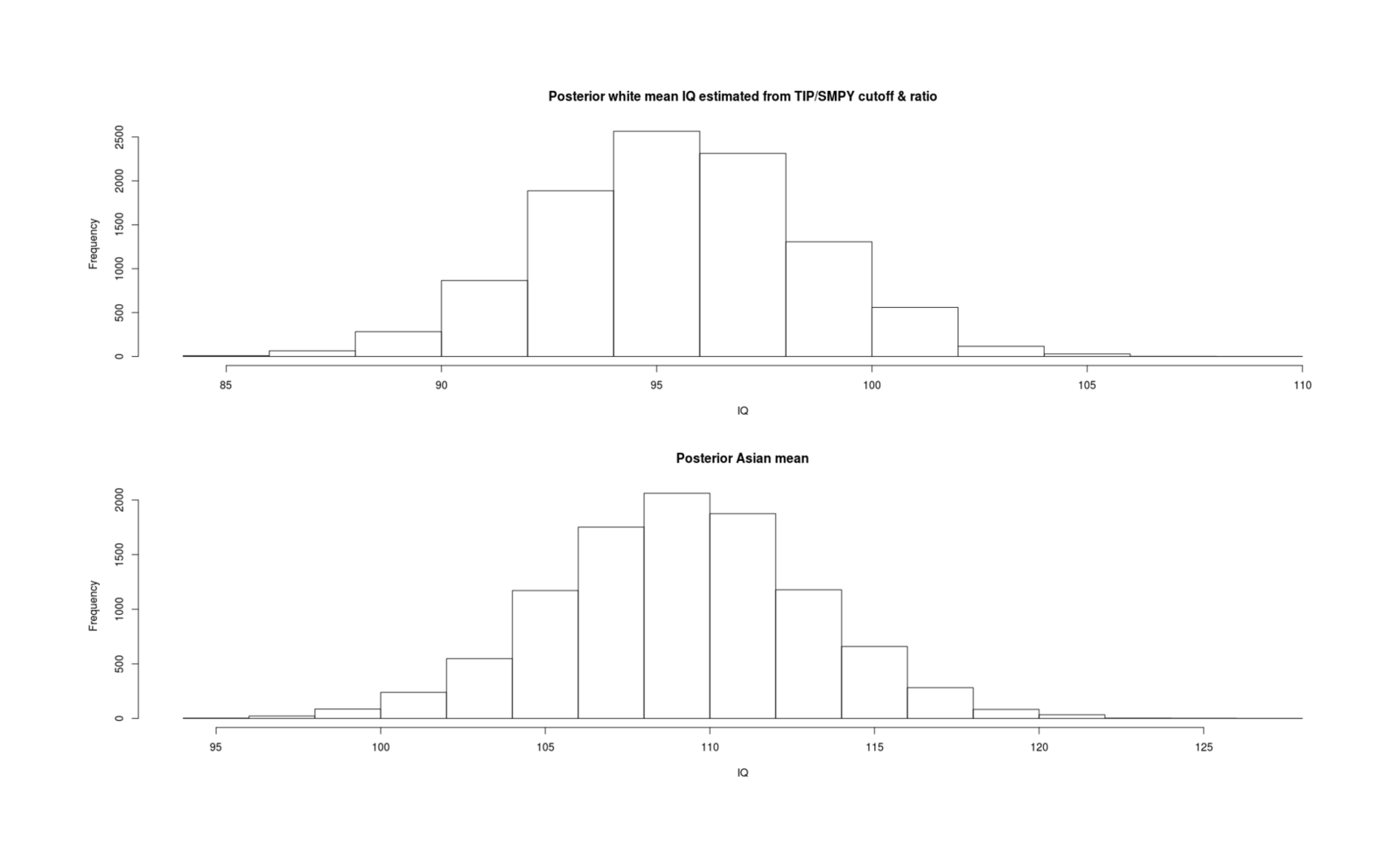
Histograms of the posterior estimate of white & Asian mean IQs ~1970 as estimated from fraction of SMPY/TIP sample using ABC
So sampling error does turn out to be substantial: our 95% credible intervals are white 90–101, Asian 101–116. Still, the overlap is minimal, with P = 99.7% that the Asian mean is higher than the white.
We are able to conclude that the rank ordering is highly likely to be correct, and the results are consistent with the conventional wisdom, so there is no prima facie case for bias in the results: the ethnic composition is in line with what one would calculate from the design of SMPY/TIP and population means.
Genius Revisited: On the Value of High IQ Elementary Schools
Great Scott! Personal Name Collisions and the Birthday Paradox
How large does can a social circle be before first names no longer suffice for identification? Scott, I’m looking at you.
MakerOfDecisions, 2016-07-29
Scott here refers to any of Scott Alexander, Scott Adams, Scott Aaronson, Scott Sumner (and to a much lesser extent, Scott Garrabrant, Orson Scott Card, and Scott H. Young); a reference to a ‘Scott’ on a site like Less Wrong is increasingly ambiguous.
When a large number of samples draw from a common pool of identifiers, collisions are common, leading to the birthday paradox: despite there being 365.25 days in the year, a classroom of just 23 people (who can cover at most 6% of the days in a year) is ~50% likely to have at least two people who share the same birthday and so birthdays cease being unique unambiguous identifiers. (Intuitively, you might expect the number to be much larger and closer to 180 than 23.)
We can verify this by simulation:
dupes <- function(a) { length(a) != length(unique(a)) }
identifiers <- function(n, ids, probabilities) { sample(1:ids, n, prob=probabilities, replace=TRUE) }
simulate <- function(n, ids, probabilities=rep(1/ids, ids), iters=10000) {
sims <- replicate(iters, { id <- identifiers(n, ids, probabilities)
return(dupes(id)) })
return(mean(sims)) }
simulate(23, 365)
# [1] 0.488
sapply(1:50, function(n) { simulate(n, 365) } )
# [1] 0.0000 0.0029 0.0059 0.0148 0.0253 0.0400 0.0585 0.0753 0.0909 0.1196 0.1431 0.1689 0.1891
# 0.2310 0.2560 0.2779 0.3142 0.3500 0.3787 0.4206 0.4383 0.4681 0.5165 0.5455 0.5722 0.5935
# [27] 0.6227 0.6491 0.6766 0.7107 0.7305 0.7536 0.7818 0.7934 0.8206 0.8302 0.8465 0.8603 0.8746
# 0.8919 0.9040 0.9134 0.9248 0.9356 0.9408 0.9490 0.9535 0.9595 0.9623 0.9732Similarly, in a group of people, it will be common for first names to overlap. (Overlaps of both first names & surnames are much more unlikely: 2017 estimate from French & Ohioan data that while almost everyone has a non-unique full name, even groups of thousands of people will have only a few duplicates.) How common? There are far more than 365.25 first names, especially as some first names are made up by parents.
Names have a highly skewed (often said to be a power law) distribution: the first few baby names make up an enormous fraction of all names, hence all the Ethan/Lucas/Mason baby boys in 2016. (One would think that parents would go out of their way to avoid too-popular names, but apparently not.)
Since there are only “10,000 things under heaven”, one might think that the top 10000 personal names would give a good guess. At what n can we expect a collision?
findN <- function(ids, targetP=0.5, startingN=1, probabilities=rep(1/ids, ids)) {
n <- startingN
collisionProbability <- 0
while (collisionProbability < targetP) {
collisionProbability <- simulate(n, ids, probabilities)
n <- n+1
}
return(n) }
findN(10000)
# [1] 118
simulate(118, 10000)
# [1] 0.5031We could also use an approximation such as the square approximation: : sqrt(2 * 10000 * 0.5) → 100 Or the similar upper bound: ceiling(sqrt(2*10000*log(2))) → 118.
So the collision point is smaller than Dunbar’s number.
But all of these are themselves upper bounds because the case in which birthdays/names are uniformly distributed is the worst case. If there is any difference in the probabilities, a collision will happen much earlier. This makes sense since if 1 birthday happens with, say, P=0.99, then it’s almost impossible to go more than 3 or 4 birthdays without a collision. Likewise, if one birthday has P=0.50, and so on down to P=$:
sapply(1:23, function(n){ simulate(n, 365, probabilities=c(0.99, rep(0.01/364, 364)))})
# [1] 0.0000 0.9789 0.9995 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
# 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
sapply(1:23, function(n){ simulate(n, 365, probabilities=c(0.5, rep(0.5/364, 364)))})
# [1] 0.0000 0.2531 0.5031 0.6915 0.8182 0.8896 0.9402 0.9666 0.9808 0.9914 0.9951 0.9973 0.9988
# 0.9993 0.9991 0.9999 1.0000 1.0000 0.9999 1.0000 1.0000 1.0000 1.0000How skewed are real names? Given Names Frequency Project provides “Popular Given Names US, 1801–198199926ya” (1990–9199926ya, 909,288 names) based on Social Security data. After deleting the first 4 lines of s1990m.txt, it can be loaded into R and the fractions used as probabilities to find the 50% collision point for US names:
names <- read.csv("s1990m.txt", header=FALSE)
summary(names)
# V1 V2
# Aaron : 1 Min. : 55.0000
# Abdiel : 1 1st Qu.: 86.0000
# Abdullah: 1 Median : 183.0000
# Abel : 1 Mean : 914.1923
# Abraham : 1 3rd Qu.: 535.5000
# Adam : 1 Max. :24435.0000
# (Other) :852
sum(names$V2)
# [1] 784377
## "Scott" as fraction of all names:
2279 / 784377
# [1] 0.0029054906
## presumably male names:
2279 / (784377*0.5)
# [1] 0.005810981199
simulate(118, nrow(names), probabilities=names$V2/sum(names$V2))
# [1] 1
findN(nrow(names), probabilities=names$V2/sum(names$V2))
# [1] 15So a more realistic analysis suggests n = 15 is where unique first names will probably break down.
This only covers the 853 most common personal names, and the more names, the higher the n has to be to trigger a collision (making 15 something of a lower upper bound); to estimate 10000, we need to fit a distribution to extrapolate below that. The log normal distribution fits reasonably well and is easy to work with:
library(fitdistrplus)
fitdist(names$V2, "lnorm")
# Fitting of the distribution ' lnorm ' by maximum likelihood
# Parameters:
# estimate Std. Error
# meanlog 5.550448321 0.04640182299
# sdlog 1.359185357 0.03281096378
simulateLN <- replicate(100, {
names <- rlnorm(10000, meanlog=5.550448321, sdlog=1.359185357)
hit <- findN(length(names), startingN=46, probabilities=names/sum(names))
return(hit)
})
median(simulateLN)
# [1] 51Since first names will cluster by age group, location, profession, and whatnot, arguably even 51 is a bit of an upper bound.
Finally, one might ask the probability of a group with a great Scott, or to put it another way, the probability of it unfortunately getting away scot-free.
This is easy to answer; the probability of having 1 or more Scotts in a group is the probability of everyone having a name other than Scott. We saw that the probability of being named Scott was P = 0.0029054906 in the name dataset. So the probability of one person not being named Scott is . So the probability of n people all being named not-Scott is 0.997n. The crossover point is ~239.
So an American social group cannot exceed n = 51 before first names begin to break down, and it is all Scott’s fault at n = 239.
Detecting Fake (Human) Markov Chain Bots
Some popular Twitter and Tumblr accounts use Markov chains trained on a corpus of writing such as Markov James Mitchens or two unrelated corpuses to create amusing mashups: programming documentation and H.P. Lovecraft’s horror/SF fiction or the King James Bible or the works of Karl Marx, Kim Kardashian and Kierkegaard, or Silicon Valley recruiting emails and Erowid drug use reports. The humor comes from the fact that the Markov chains have no understanding and are merely programs producing gibberish that occasionally present striking juxtapositions or insights. Much of their appeal derives in large part from the fact that while humans curate them, humans don’t write them. They depend on this authenticity to be striking.
Of course, there’s always the temptation to edit them or write them wholesale, perhaps because the Markov chains aren’t cooperating in producing any comedy gold to tweet that day, which deceives the reader. This poses an inverse Turing test: how would you detect a fake Markov chain account, that is, one where a human is pretending to be a computer and writing some of the text?
Markov chains are trained on a specific corpus and are a probabilistic generative model which encode the probability that a word X follows another word Y for all the words in that corpus (and similarly if they are operating on letters or on n-grams); there is no state or memory or ‘look back’ or ability to model recursion. To generate text, one simply picks a random word Y, looks up the probabilities of all the words A…Z from Y, and picks a word at random weighted by those probabilities; then repeat indefinitely. Conversely, one could also use it to calculate the likelihood of a given text by multiplying the probability of each word in the text conditional on the previous one.
One difficulty is the potential for double-use of data: the first pass through a Markov chain account is already applying to the data a highly flexible Bayesian neural network with billions of parameters (one’s brain). If one spots an ‘anomalous’ dataset and subsequent analysis confirms it, what does this mean? I am reminded of one past incident: someone had lost a great deal of money on a Bitcoin gambling website, and suspected the site had defrauded him. But he had contacted me only because he had had unusual losses. What does an analysis mean? Imagine that the top 1% of losers get angry and start looking into whether they were cheated; they go to a statistician who duly computes that based on the number of games played, there is a p = 0.01 that they would lose as much or more as they did… If one had all the gambling records, one could look at the overall patterns and see if there are more losers than there should be given the rules of the game and a supposedly fair random number generator, but what does one do with 1 self-selected player? The data generation process is certainly neither random nor ‘ignorable’ nor modelable without dubious assumptions.
A few possible attacks come to mind:
observation of malformed syntax or lack of long-range dependencies
vocabulary or output outside an independently trained Markov chain’s domain
unusually low likelihood for an independently trained Markov chain to generate known samples
unusually low likelihood for an independently trained Markov chain to generate known samples compared to newly generated samples filtered at a 1-in-100s quality level
unusually high quality of known samples compared to newly generated samples from independently trained Markov chain filtered at a 1-in-100s quality level, tested nonparametrically or parametrically as a mixture model
Markov chains produce realistic-looking output and are efficient to create & run, but, compared to RNNs, they notoriously model recursive syntax poorly, such as nested parentheses (since they have no way of remembering whether a parenthetical comment had been started), and cannot extrapolate—for example, a word-level Markov chain can’t create new words, and would require n-grams to have available fragments of words which could be recombined. The memory-less nature of Markov chains also means that, lacking any memory which could model the ‘long-range correlations’ found in natural English text like systematic use of particular names/topics/vocabulary, larger samples quickly veer off-topic and become gibberish and lack any coherency possibly even inside a single sentence. (RNNs also have this problem, but somewhat less.)
With the limits of a Markov chain in mind, it would be easy to detect faked Markov chain output with large samples: it is just difficult for a human to deliberately generate long text which is as nonsensical and syntactically invalid as a Markov chain creates, for the same reason an unpracticed human is a remarkably bad random number generator. However, for this same reason the selected Markov samples tend to be very short, usually no more than a sentence. It might be possible to measure this on the samples as a whole and observe higher entropy or memoryless-ness (eg. by measuring compression performance or efficiency of a Markov chain in modeling the samples), but I would guess that usually the samples are not long enough or large enough for this to have reasonable statistical power as a test. This eliminates the easiest test.
Since the corpus is known in many of these cases, we can assume access to a Markov chain model which is similar (if not identical) to the one which supposedly wrote all the tweets. This gives us several possibilities.
We could exploit the lack of creativity of Markov chains and look for anything in the tweets which is not present in the original corpus. For example, if a word like “cromulent” appears neither in the Puppet documentation nor (having been coined in 199629ya, 59 years after he died) in H.P. Lovecraft’s fiction, then it would have a probability of 0 of being generated by any Puppet/Lovecraft Markov chain (as no word will have any transition probability to it). Such extra-corporal vocabulary immediately proves human authorship.
Continuing this same logic, we could take the corpus, train our own Markov chain (which will at least be similar), and use it to calculate the likelihood of all the tweets. A human-written tweet may be possible for the Markov chain to have written, but it will be far more unlikely than most of the ones the Markov chain actually wrote & were selected. So we would see that most of the tweets have reasonable log likelihoods, but that our suspicious ones will be far more extreme. (If the Markov chains are word-level, this test subsumes the impossible-word test: any tweet with a word not in the corpus, and hence not represented in the Markov chain, will have a meaningless likelihood.)
This likelihood test might not help if they are all equally extreme, in which case one could use our Markov chain in another manner, as a generative model, to try to estimate the likelihood of getting as great a tweet. For this, one samples several thousand samples from our Markov chain, and screens them for good ones. This creates an empirical distribution of the likelihoods of good tweets conditional on the null hypothesis of a Markov chain author; in this case, the null hypothesis is known to be true by construction. Then to test, one compares the known-Markov-chain tweets with the likelihoods of the suspect tweets (perhaps with a permutation test). They should be similar.
Alternately, if one doesn’t want to use likelihoods as a measure of improbability, one could instead use some human measure of funniness like having rating the originals and the samples on a scale 1-5, and comparing them. The original poster is probably not screening more than a few hundred generated tweets for each selected tweet, so given a similar level of stringency, one’s generated tweets should be equally good; if the originals turn out to be extremely better than yours, to a level where you would have to screen thousands of random samples, that is highly suspicious and suggests the originals were ‘too good to be true’.
With ratings or likelihoods, one could try to assume a decreasing distribution like an exponential: most samples will be incoherent and totally unfunny, many will be slightly funny, a few will be funny, and a very few will be very funny. The ratings on samples generated from our Markov chain will probably follow a smooth distribution. However, if a human is authoring some in an attempt to spice things up, they will be above the average of the Markov chain (otherwise why bother with cheating?), and if there is a substantial number of them, this will create an anomaly in the ratings of the originals—a ‘bump’ indicating that the tweets are coming from two different populations. In this case, it can be modeled as a mixture model with either k = 1 or k = 2, and the p-value or Bayesian posterior probability calculated for 1 vs 2.
Optimal Existential Risk Reduction Investment
An existential risk is any risk which destroys or permanently cripples human civilization, such as an asteroid strike or pandemic. Since humanity might otherwise continue for millions of years, creating untold trillions of humans and colonizing the galaxy, human extinction represents the loss of literally astronomical amounts of utility. The loss is greater than any disaster up to extinction levels, as humanity can always recover from lesser disasters; but there is no recovery from a total destruction. Thus, the expected value of even a slight reduction in an exotic risk ought to itself be astronomical, or at least extremely large; under plausible values for well-characterized x-risks like asteroid strikes or nuclear war or pandemic, preventing them may be the charitable spending with the highest expected value and they should be receiving all charitable expenditures.
This strikes people as odd and dangerous reasoning. Is it really true that we should be spending almost unlimited amounts of money on these things and not otherwise extremely compelling charities like distributing malaria nets in Africa to save millions of lives or vaccine distribution or funding research into ending aging? And if we should, how do we choose what fraction to spend on global warming rather than artificial intelligence? What if someone discovers an entirely new x-risk not previously considered, like nearby supernovas or vacuum collapses or nanotechnology ‘grey goo’?
Thinking historically, it’s clear in retrospect that someone concerned about x-risk would be better off not going after the terminal goal of x-risk reduction but instead spending their money on instrumental goals such as science/technology or economic growth.
Imagine someone in England in 1500 who reasons the same way about x-risk: humanity might be destroyed, so preventing that is the most important task possible. He then spends the rest of his life researching the Devil and the Apocalypse. Such research is, unfortunately, of no value whatsoever unless it produces arguments for atheism demonstrating that that entire line of enquiry is useless and should not be pursued further. But as the Industrial and Scientific Revolutions were just beginning, with exponential increases in global wealth and science and technology and population, ultimately leading to vaccine technology, rockets and space programs, and enough wealth to fund all manner of investments in x-risk reduction, he could instead had made a perhaps small but real contribution by contributing to economic growth by work & investment or making scientific discoveries.
For example, Isaac Newton’s discoveries in astronomy and the laws of motion helped inaugurate threads of work that led directly to space satellites which can watch for asteroids with Earth-crossing orbits. Isaac Newton himself was concerned with x-risk, as he feared that the Great Comet of 1680 would, centuries hence, plunge into the Sun and cause expansion destroying the Earth and humanity. What could Newton have done to directly reduce this x-risk at the time? Absolutely nothing. There were no feasible counter-measures nor any foreseeable technologies which could forestall a comet or protect humanity from the Sun engulfing the Earth; there was not and still is not a mine or bomb shelter deep enough for that. What he could have done is close to what he did do: make fundamental advances in science which posterity could build on and one day be rich and wise enough to do something about the x-risk. As it happens, Newton was not quite right about the Great Comet (comets are not a meaningful fraction of the Sun’s mass) but there was a similar x-risk he was unaware of: giant asteroid impacts. And the solutions to a giant comet—observe all comets carefully to project their future orbits, destroy it, redirect its orbit, evacuate human colonists to safety to unaffected planets (Newton suggested the satellites of the gas giants)—are much the same as for a giant asteroid impact, and all benefit from economic growth & greater science/technology (someone has to pay for, and design those satellites and spacecraft, after all).
Economic wealth & science/technology are all-purpose goods: they are useful for compound growth, and can also be spent on x-risk reduction. They are the ultimate instrumental goods. If one is badly ignorant, or poor, or unable to meaningfully reduce an x-risk, one is better off accepting the x-risk and instead spending resources on fixing the former problems. One would prefer to get rid of the x-risk as soon as possible, of course, but given one’s starting position, there may simply be no better strategy and the risk must be accepted.
This raises the question: what is the optimal distribution of resources to economic growth vs x-risk reduction over time which maximizes expected utility?
Intuitively, we might expect something like early on investing nothing at all in x-risk reduction as there’s not much money available to be spent, and money spent now costs a lot of money down the line in lost compound growth; and then as the economy reaches modern levels and the opportunity cost of x-risk becomes dire, money is increasingly diverted to x-risk reduction. One might analogize it to insurance—poor people skimp on insurance because they need the money for other things which hopefully will pay off later like education or starting a business, while rich people want to buy lots of insurance because they already have enough and they fear the risks. If this were an investment question, a good strategy would be something like the Kelly criterion or probability matching strategies like Thompson sampling: even if the expected value of x-risk reduction is higher than other investments, it only pays off very rarely and so receives a very small fraction of one’s investments. However, it’s not clear that the Kelly criterion or Thompson sampling are optimal or even relevant: because while Kelly avoids bankruptcy in the form of gambler’s ruin but does so only by making arbitrarily small bets to avoid going bankrupt & refusing to ever risk one’s entire wealth; with x-risks, the ‘bankruptcy’ (extinction) can’t be avoided so easily, as the risk is there whether you like it or not, and one cannot turn it to 0. (This comes up often in discussion of why the Kelly criterion is relevant to decision-making under risk; see also 2011 and the niche area of “evolutionary finance” like et al 2008/Lensberg & Schenk-2006 which draws connections between the Kelly criterion, probability matching, long-term survival & evolutionary fitness.) In economics, similar questions are often dealt with in terms of the life-cycle hypothesis in which economic agents strive to maximize their utility over a career/lifetime while avoiding inefficient intertemporal allocation of wealth (as Mark Twain put it, “when in youth a dollar would bring a hundred pleasures, you can’t have it. When you are old, you get it & there is nothing worth buying with it then. It’s an epitome of life. The first half of it consists of the capacity to enjoy without the chance; the last half consists of the chance without the capacity.”); in the life-cycle, one tries to build wealth as quickly as possible while young, even going into debt for investments like a college education, then begins saving up, consuming some, until retirement, at which point one consumes it all until one dies. But as far as I’ve seen any results, life-cycle models tend to not include any mechanism for spending in order to reduce mortality/aging and accept the risk of death as a given.
We could create a simple Markov decision process model. An agent (humanity), each time period (year), has a certain amount of wealth and an x-risk probability P. In this period, it can choose to allocate that wealth between economic growth, in which case it receives that investment plus a return, and it can buy a permanent percentage reduction in the x-risk for a fixed sum. For the reward, the x-risk is binary sampled with probability P; if the sample is true, then the reward is 0 and the decision process terminates, else the reward is the wealth and the process continues. Let’s imagine that this process can run up to 10,000 time periods, with a starting wealth of $248 billion (Angus Deaton’s estimate of PPP world GDP in 1500 https://en.wikipedia.org/wiki/List_of_regions_by_past_GDP_%28PPP%29 ), the economic growth rate is 2% (the long-run real growth rate of the global economy), the existential risk probability is 0.1% per year (arbitrarily chosen), and one can buy a reduction of 1% for a billion dollars. (We’ll work in trillions units to help numeric stability.) What strategy maximizes the cumulative rewards? A few simple ones come to mind:
the agent could simply ignore the x-risk and reinvests all wealth, which to a first approximation, is the strategy which has been followed throughout human history and is primarily followed now (lumping together NASA’s Spaceguard program, biowarfare and pandemic research, AI risk research etc probably doesn’t come to more than $1-2b a year in 2016). This maximizes economic growth rate but may backfire as the x-risk never gets reduced.
the agent could spend the full gain in its wealth from economic growth (2%) on x-risk reduction. The wealth doesn’t grow and the returns from x-risk reduction do diminish, but the x-risk is at least reduced greatly over time.
the agent could implement a sort of probability matching: it spends on x-risk reduction a fraction of its wealth equal to the current P. This reduces how much is spent on extremely small x-risk reductions, but it might be suboptimal because it’ll pay the largest fraction of its economy in the first time period, then second-largest in the second time period and so on, losing out on the potential compounding.
a more complicated hybrid strategy might work: it maximizes wealth like #1 for the first n time periods (eg. n = 516), and then it switches to #2 for the remaining time period
like #4, but switching from #1 to #3 for the remaining time periods.
constantInvestmentAgent <- function (t, w, xrp) { return(c(w, 0)) }
constantReductionAgent <- function (t, w, xrp) { drawdown <- 0.9803921573; return(c(drawdown*w, (1-drawdown)*w)) }
probabilityMatchAgent <- function (t, w, xrp) { return(c(w*(1-xrp), w*xrp)) }
investThenReduceAgent <- function (t, w, xrp, n=516) { if (t<n) { return(constantInvestmentAgent(t, w, xrp)) } else { return(constantReductionAgent(t, w, xrp)) } }
investThenMatchAgent <- function (t, w, xrp, n=516) { if (t<n) { return(constantInvestmentAgent(t, w, xrp)) } else { return(probabilityMatchAgent(t, w, xrp)) } }
simulateWorld <- function(agent, t=10000) {
initialW <- 0.248
initialP <- 0.001
df <- data.frame(T=0, Wealth=initialW, XriskP=initialP)
for (i in 1:t) {
last <- tail(df, n=1)
xrisk <- rbinom(1,1, p=last$XriskP)
if (xrisk) { break; } else {
choices <- agent(last$T, last$Wealth, last$XriskP)
newXriskP <- last$XriskP * (1 - 0.01)^(choices[2] / 0.001)
newWealth <- choices[1] * 1.02
df <- rbind(df, data.frame(T=i, Wealth=newWealth, XriskP=newXriskP))
}
}
df$Reward <- cumsum(df$Wealth)
return(df)
}
library(parallel); library(plyr)
simulateWorlds <- function(agent, iters=1000) {
mean(ldply(mclapply(1:iters, function(i) { tail(simulateWorld(agent), n=1)$Reward }))$V1) }
simulateWorlds(constantReductionAgent)
# [1] 2423.308636
simulateWorlds(investThenReduceAgent)
# [1] 10127204.73
simulateWorlds(constantInvestmentAgent)
# [1] 1.154991741e+76
simulateWorlds(investThenMatchAgent)
# [1] 7.53514145e+86
## Optimize the switch point:
which.max(sapply(seq(1, 10000, by=100), function(N) { simulateWorlds(function(t,w,xrp) { investThenMatchAgent(t, w, xrp, n=N) }, iters=100)}))
# [1] 3
simulateWorlds(function(t,w,xrp) { investThenMatchAgent(t, w, xrp, n=300) })
# [1] 9.331170221e+86
simulateWorlds(probabilityMatchAgent)
# [1] 1.006834082e+87So of our 5 strategies, the constant reduction agent performs the worst (probably because with economic growth choked off, it can only buy small x-risk reductions), followed by the invest-then-reduce agent; then the ‘get rich before you get old’ constant investment agent manages to often attain very high growth rates when it’s lucky enough that x-risks don’t strike early on; but far better than any of them, by orders of magnitude, are the partial and full probability matching agents. The partial probability matching agent turns out to have a suboptimal switch point t = 516, and a more careful search of switch points finds that t~=300 is the best switch point and it exceeds the pure probability matcher which matches from the start.
What’s going on there? I suspect it’s something similar to the difference in multi-armed bandit problems between the asymptotically optimal solution and the optimal solution for a fixed horizon found using dynamic programming: in the former scenario, there’s an indefinite amount of time to do any exploration or investment in information, but in the latter, there’s only a finite time left and exploration/growth must be done up front and then the optimal decision increasingly shifts to exploitation rather than growth.
Why does probability matching in general work so well? It may simply be because it’s the only baseline strategy which adjusts its xrisk investment over time.
This doesn’t demonstrate that probability matching is optimal, just that it beats the other baseline strategies. Other strategies could be used to decrease xrisk investment over time—instead of being proportional to xrisk P, it could shrink linearly over time, or by square root, or logarithmically, or…
What reinforcement learning techniques might we use to solve this?
This problem represents a large Markov Decision Process with 1 discrete state variable (time, t = 0-10000), 2 continuous state variables (wealth, and risk probability), and 1 continuous action (fraction of growth to allocate to the economy vs existential risk reduction). The continuous action can be discretized into 11 actions without probably losing anything (allocate 100%/90%..10%/0%), but the 2 state variables can’t be discretized easily because they can span many orders of magnitude.
dynamic programming a decision tree with backwards induction: optimal, but requires discrete actions and state variables, and even if discretized, 10000 time steps would be infeasibly large.
standard tabular learning: Q-learning, SARSA, temporal differences: requires discrete actions and state variables
Deep Q-Networks: requires discrete actions, but not state variables
MDP solvers: value iteration etc: optimal, but requires discrete actions and state variables
hybrid MDP solvers: optimal, and can handle a limited amount of continuous state variables (but not continuous actions), which would work here; but high quality software implementations are rarely available.
One such hybrid MDP solver is
hmpd, which solves problems specified in the PDDL Lisp-like DSL (judging from the examples, a version with probabilistic effects, so PPDDL 1.0?). After trying to write down a PPDDL model corresponding to this scenario, it seems that PPDDL is unable to represent probabilities or rewards which change with time and so cannot represent the increase in wealth or decrease in x-risk probability.policy gradients: can handle continuous state variables & actions but are highly complex and unstable; high quality software implementations are unavailable
Of the possible options, a DQN agent seems like the best choice: a small neural network should be able to handle the problem and DQN only requires the actions to be discretized. reinforce.js provides a DQN implementation in JS which I’ve used before, so I start there by rewriting the problem in JS
var script = document.createElement("script");
script.src = "https://gwern.net/doc/reinforcement-learning/armstrong-controlproblem/2016-02-02-karpathy-rl.js";
document.body.appendChild(script);
// environment: t, w, xrp
function simulate(environment, w_weight, xrp_weight) {
var xrisk = Math.random() < environment.xrp
if (xrisk) {
return {reward: -100, alive: false, t: environment.t, w: environment.w, xrp: environment.xrp};
} else {
return {reward: Math.log(environment.w), alive: true, t: environment.t+1,
w: environment.w*w_weight*1.02, xrp: environment.xrp * (Math.pow((1 - 0.01), (xrp_weight / 0.001))) }
}
}
var defaultState = {t: 0, w: 0.248, xrp: 0.01}
// simulate(defaultState, 0.99, 0.01)
// simulate(defaultState, 0.99, 0.01)
var env = {};
env.getNumStates = function() { return 3; }; // there are only 3 state variables: t/w/xrp
env.getMaxNumActions = function() { return 11; }; // we'll specify 10 possible allocations: 1/0, 0.998/0.002 .. 0.98/0.02
var spec = {
num_hidden_units: 200,
experience_add_every: 20,
learning_steps_per_iteration: 1,
experience_size: 1000000,
alpha: 0.01,
epsilon: 1.0,
gamma: 0.99 // minimal discounting
};
var agent = new RL.DQNAgent(env, spec);
var total_reward = 0;
state = defaultState;
spec.epsilon = 1.0; // reset epsilon if we've been running the loop multiple times
for(var i=0; i < 10000*3000; i++) {
var action = agent.act(state)
state = simulate(state, 1-(action/500), 0+(action/500) );
agent.learn(state.reward);
total_reward = total_reward + state.reward;
if (Number.isInteger(Math.log(i) / Math.log(10)) ) { spec.epsilon = spec.epsilon / 1.5; } // decrease exploration
if (!state.alive || state.t >= 10000) { // if killed by x-risk or horizon reached
console.log(state.t, state.w, state.xrp, total_reward);
total_reward = 0;
state = defaultState;
}
}
//exercise the trained agent to see how it thinks
total_reward=0
state=defaultState;
spec.epsilon = 0;
for (var t=0; t < 10000; t++) {
action = agent.act(state)
state = simulate(state, 1-(action/500), 0+(action/500) );
total_reward = total_reward + state.reward
console.log(action, state, total_reward);
}After a day of training, the DQN agent had learned to get up to 5e41, which was disappointingly inferior to the constant investment & probability matching agents (1e87). The NN looks big enough for this problem and the experience replay buffer was more than adequate; NNs in RL are known to have issues with the reward, though, and typically ‘clamp’ the reward to a narrow range, so I suspected that rewards going up to 5e41 (interpreting wealth on each turn as the reward) might be playing havoc with convergence, and switched the reward to log wealth instead. This did not make a noticeable difference overnight (aside from the DQN agent now achieving 9.5e41). I wondered if the risk was too rare for easy learning and 100 neurons was not enough to approximate the curve over time, so I fixed a bug I noticed where the simulation did not terminate at t=10000, doubled led the neuron count, increased the initial x-risk to 1%, and began a fresh run. After 1 day, it reached 9.4e41 total reward (unlogged).
Cumulative log score for DQN after tweaks and ~2h of training: regularly reaches ~470k when it doesn’t die immediately (which happens ~1/20 of the time). In comparison, probability-matching agent averages a cumulative log score of 866k. After 2 days of training, the DQN had improved only slightly; the on-policy strategy appears mostly random aside from having driven the xrisk probability down to what appears to be the smallest float JS supports, so it still had not learned a meaningful compromise between xrisk reduction and investment.
TODO: revisit with MCTS at some point?
Model Criticism via Machine Learning
In “Deep learning, model checking, AI, the no-homunculus principle, and the unitary nature of consciousness”, Andrew Gelman writes
Here’s how we put it on the very first page of our book:
The process of Bayesian data analysis can be idealized by dividing it into the following three steps:
Setting up a full probability model - a joint probability distribution for all observable and unobservable quantities in a problem. The model should be consistent with knowledge about the underlying scientific problem and the data collection process.
Conditioning on observed data: calculating and interpreting the appropriate posterior distribution—the conditional probability distribution of the unobserved quantities of ultimate interest, given the observed data.
Evaluating the fit of the model and the implications of the resulting posterior distribution: how well does the model fit the data, are the substantive conclusions reasonable, and how sensitive are the results to the modeling assumptions in step 1? In response, one can alter or expand the model and repeat the three steps.
How does this fit in with goals of performing statistical analysis using artificial intelligence?
3. The third step—identifying model misfit and, in response, figuring out how to improve the model—seems like the toughest part to automate. We often learn of model problems through open-ended exploratory data analysis, where we look at data to find unexpected patterns and compare inferences to our vast stores of statistical experience and subject-matter knowledge. Indeed, one of my main pieces of advice to statisticians is to integrate that knowledge into statistical analysis, both in the form of formal prior distributions and in a willingness to carefully interrogate the implications of fitted models.
One way of looking at step #3 is to treat the human statistician as another model: specifically, he is a large neural network with trillions of parameters, who has been trained to look for anomalies & model misspecification, and to fix them when he finds them, retraining the model, until he can no longer easily distinguish the original data from the model’s predictions or samples. As he is such a large model with the ability to represent and infer a large class of nonlinearities, he can usually easily spot flaws where the current model’s distribution differs from the true distribution.
This bears a considerable resemblance to the increasing popularity of “generative adversarial networks” (GANs): using pairs of neural networks, one of which tries to generate realistic data, and a second which tries to classify or discriminate between real and realistic data. As the second learns ways in which the current realistic data is unrealistic, the first gets feedback on what it’s doing wrong and fixes it. So the loop is very similar, but fully automated. (A third set of approaches this resembles is actor-critic reinforcement learning algorithms.)
If we consider the kinds of models which are being critiqued, and what is critiquing, this gives us 4 possible combinations:
simple |
complex |
|
|---|---|---|
simple |
model fit indexes+linear model |
statistician+linear model |
complex |
model fit indexes+ML |
ML+ML (eg. GANs) |
Simple/simple is useful for cases like linear regression where classic methods like examining residuals or R^2s or Cook indexes can often flag problems with the model.
Simple/complex is also useful, as the human statistician can spot additional problems.
Complex/simple is probably useless, as the NNs may easily have severe problems but will have fit any simple linear structure and fool regular diagnostics.
Complex/complex can be very useful in machine learning, but in different ways from a good simple model.
Fast, simple, general—a good statistical method lets you choose one; a great method lets you choose two. (Consider linear models, decision trees, NNs, MCMC, ABC, discrete Bayesian networks, and exponential family vs nonparametric methods as examples of the tradeoffs here.)
So is quadrant 2 fully populated by human statisticians? We wouldn’t necessarily want to use GANs for everything we use statisticians for now, because neural networks can be too powerful and what we want from our models is often some sort of clear answer like “does X predict Y?” and simplicity. But we could replace the statistician with some other powerful critic from machine learning—like a NN, SVM, random forest, or other ensemble. So instead of having two NNs fighting each other as in a GAN, we simply have one specified model, and a NN which tries to find flaws in it, which can then be reported to the user. The loop then becomes: write down and fit a model to the real data; generative posterior predictive samples from the distribution; train a small NN on real data vs predictive data; the classification performance measures the plausibility of the predictive samples (perhaps something like a KL divergence), giving a measure of the model quality, and flags data points which are particularly easily distinguished as real; the human statistician now knows exactly which data points are not captured by the model and can modify the model; repeat until the NN’s performance declines to chance.
Let’s try an example. We’ll set up a simple linear model regression Y ~ A + B + C with a few problems in it:
the trend is not linear but slightly quadratic
the outcome variable is also right-censored at a certain point
and finally, the measured covariates have been rounded
set.seed(2016-11-23)
n <- 10000
ceiling <- 1
a <- rnorm(n)
b <- rnorm(n)
c <- rnorm(n)
y <- 0 + 0.5*a + 0.5*b + 0.5*c^2 + rnorm(n)
y_censored <- ifelse(y>=3, 3, y)
df <- data.frame(Y=y_censored, A=round(a, digits=1), B=round(b, digits=1), C=round(c, digits=1))
l <- lm(Y ~ A + B + C, data=df)
summary(l)
plot(l)
plot(df$Y, predict(l, df))
l2 <- lm(Y ~ A + B + I(C^2), data=df)
summary(l2)
plot(df$Y, predict(l2, df))The censoring shows up immediately on the diagnostics as an excess of actual points at 3, but the quadraticity is subtler, and I’m not sure I can see the rounding at all.
library(randomForest)
## First, random forest performance under the null hypothesis
modelNull <- data.frame(Y=c(df$Y, df$Y), Real=c(rep(1, n), rep(0, n)), A=c(df$A, df$A), B=c(df$B, df$B), C=c(df$C, df$C))
r_n <- randomForest(as.ordered(Real) ~ Y + A + B + C, modelNull); r_n
# Type of random forest: classification
# Number of trees: 500
# No. of variables tried at each split: 2
#
# OOB estimate of error rate: 100%
# Confusion matrix:
# 0 1 class.error
# 0 0 10000 1
# 1 10000 0 1
modelPredictions <- data.frame(Y=c(df$Y, predict(l, df)), Real=c(rep(1, n), rep(0, n)), A=c(df$A, df$A), B=c(df$B, df$B), C=c(df$C, df$C))
r <- randomForest(as.ordered(Real) ~ Y + A + B + C, modelPredictions); r
# Type of random forest: classification
# Number of trees: 500
# No. of variables tried at each split: 2
#
# OOB estimate of error rate: 6.59%
# Confusion matrix:
# 0 1 class.error
# 0 9883 117 0.0117
# 1 1200 8800 0.1200
## many of the LM predictions are identical, but the RF is not simply memorizing them as we can jitter predictions and still get the same classification performance:
modelPredictions$Y2 <- jitter(modelPredictions$Y)
randomForest(as.ordered(Real) ~ Y2 + A + B + C, modelPredictions)
#... Type of random forest: classification
# Number of trees: 500
# No. of variables tried at each split: 2
#
# OOB estimate of error rate: 6.57%
# Confusion matrix:
# 0 1 class.error
# 0 9887 113 0.0113
# 1 1200 8800 0.1200Note we need to be careful about collecting the posterior predictive samples: if we collect 10000 posterior samples for each of the 10000 datapoints, we’ll store 100002 numbers which may cause problems. 1 should be enough.
library(runjags)
model <- 'model {
for (i in 1:n) {
mean[i] <- mu + betaA*A[i] + betaB*B[i] + betaC*C[i]
Y[i] ~ dnorm(mean[i], tau)
}
sd ~ dgamma(0.01, 0.01)
tau <- 1/sqrt(sd)
mu ~ dnorm(0, 100)
betaA ~ dnorm(0, 100)
betaB ~ dnorm(0, 100)
betaC ~ dnorm(0, 100)
}'
model <- run.jags(model, data = with(df, list(Y=c(Y, rep(NA, nrow(df))), A=c(A,A), B=c(B,B), C=c(C,C), n=2*nrow(df))), inits=list(mu=0.45, sd=0.94, betaA=0.47, betaB=0.46, betaC=0), monitor=c("Y"), n.chains = 1, sample=1)
posterior_predictive <- tail(n=10000, model$mcmc[[1]][1,])
plot(df$Y, posterior_predictive)
modelPredictions_r <- data.frame(Y=c(df$Y, posterior_predictive), Real=c(rep(1, n), rep(0, n)), A=c(df$A, df$A), B=c(df$B, df$B), C=c(df$C, df$C))
r <- randomForest(as.ordered(Real) ~ Y + A + B + C, modelPredictions_r); r
# OOB estimate of error rate: 49.11%
# Confusion matrix:
# 0 1 class.error
# 0 4953 5047 0.5047
# 1 4776 5224 0.4776model_rounded <- 'model {
for (i in 1:n) {
roundA[i] ~ dround(A[i], 3)
roundB[i] ~ dround(B[i], 3)
roundC[i] ~ dround(C[i], 3)
mean[i] <- mu + betaA*roundA[i] + betaB*roundB[i] + betaC*roundC[i]
Y[i] ~ dnorm(mean[i], tau)
}
sd ~ dgamma(0.01, 0.01)
tau <- 1/sqrt(sd)
mu ~ dnorm(0, 100)
betaA ~ dnorm(0, 100)
betaB ~ dnorm(0, 100)
betaC ~ dnorm(0, 100)
}'
model_r <- run.jags(model_rounded, data = with(df, list(Y=c(Y, rep(NA, nrow(df))), A=c(A,A), B=c(B,B), C=c(C,C), n=2*nrow(df))), inits=list(mu=0.45, sd=0.94, betaA=0.47, betaB=0.46, betaC=0), monitor=c("Y"), n.chains = 1, sample=1)
posterior_samples <- tail(n=10000, model_r$mcmc[[1]][1,])
posterior_predictive <- ifelse(posterior_samples>=3, 3, posterior_samples)
plot(df$Y, posterior_predictive)
modelPredictions_r <- data.frame(Y=c(df$Y, posterior_predictive), Real=c(rep(1, n), rep(0, n)), A=c(df$A, df$A), B=c(df$B, df$B), C=c(df$C, df$C))
r_r <- randomForest(as.ordered(Real) ~ Y + A + B + C, modelPredictions_r); r_r
# OOB estimate of error rate: 50.48%
# Confusion matrix:
# 0 1 class.error
# 0 4814 5186 0.5186
# 1 4909 5091 0.4909model_rounded_censor <- 'model {
for (i in 1:n) {
roundA[i] ~ dround(A[i], 3)
roundB[i] ~ dround(B[i], 3)
roundC[i] ~ dround(C[i], 3)
mean[i] <- mu + betaA*roundA[i] + betaB*roundB[i] + betaC*roundC[i]
Y[i] ~ dnorm(mean[i], tau)
is.censored[i] ~ dinterval(Y[i], c)
}
sd ~ dgamma(0.01, 0.01)
tau <- 1/sqrt(sd)
mu ~ dnorm(0, 100)
betaA ~ dnorm(0, 100)
betaB ~ dnorm(0, 100)
betaC ~ dnorm(0, 100)
}'
model_r_c <- run.jags(model_rounded_censor, data = with(df, list(Y=c(Y, rep(NA, nrow(df))), A=c(A,A), B=c(B,B), C=c(C,C), n=2*nrow(df), is.censored=c(as.integer(Y==3), as.integer(Y==3)), c=3)), inits=list(mu=0.37, sd=1, betaA=0.42, betaB=0.40, betaC=0), monitor=c("Y"), n.chains = 1, adapt=0, burnin=500, sample=1)
posterior_samples <- tail(n=10000, model_r_c$mcmc[[1]][1,])
posterior_predictive <- ifelse(posterior_samples>=3, 3, posterior_samples)
modelPredictions_r_c <- data.frame(Y=c(df$Y, posterior_predictive), Real=c(rep(1, n), rep(0, n)), A=c(df$A, df$A), B=c(df$B, df$B), C=c(df$C, df$C))
r_r_c <- randomForest(as.ordered(Real) ~ Y + A + B + C, modelPredictions_r_c); r_r_c
# OOB estimate of error rate: 53.67%
# Confusion matrix:
# 0 1 class.error
# 0 4490 5510 0.5510
# 1 5224 4776 0.5224model_rounded_censor_quadratic <- 'model {
for (i in 1:n) {
roundA[i] ~ dround(A[i], 3)
roundB[i] ~ dround(B[i], 3)
roundC[i] ~ dround(C[i], 3)
mean[i] <- mu + betaA*roundA[i] + betaB*roundB[i] + betaC*roundC[i]^2
Y[i] ~ dnorm(mean[i], tau)
is.censored[i] ~ dinterval(Y[i], c)
}
sd ~ dgamma(0.01, 0.01)
tau <- 1/sqrt(sd)
mu ~ dnorm(0, 100)
betaA ~ dnorm(0, 100)
betaB ~ dnorm(0, 100)
betaC ~ dnorm(0, 100)
}'
model_r_c_q <- run.jags(model_rounded_censor_quadratic, data = with(df, list(Y=c(Y, rep(NA, nrow(df))), A=c(A,A), B=c(B,B), C=c(C,C), n=2*nrow(df), is.censored=c(as.integer(Y==3), as.integer(Y==3)), c=3)), inits=list(mu=0.37, sd=1, betaA=0.42, betaB=0.40, betaC=0), monitor=c("Y"), n.chains = 1, adapt=0, burnin=500, sample=1)
posterior_samples <- tail(n=10000, model_r_c_q$mcmc[[1]][1,])
posterior_predictive <- ifelse(posterior_samples>=3, 3, posterior_samples)
modelPredictions_r_c_q <- data.frame(Y=c(df$Y, posterior_predictive), Real=c(rep(1, n), rep(0, n)), A=c(df$A, df$A), B=c(df$B, df$B), C=c(df$C, df$C))
r_r_c_q <- randomForest(as.ordered(Real) ~ Y + A + B + C, modelPredictions_r_c_q); r_r_c_q
# OOB estimate of error rate: 61.02%
# Confusion matrix:
# 0 1 class.error
# 0 3924 6076 0.6076
# 1 6127 3873 0.6127
trueNegatives <- modelPredictions_r_c_q[predict(r_r_c_q) == 0 & modelPredictions_r_c_q$Real == 0,]Where can we go with this? The ML techniques can be used to rank existing Bayesian models in an effective if unprincipled way. Techniques which quantify uncertainty like Bayesian neural networks could give more effective feedback by highlighting the points the Bayesian NN is most certain are fake, guiding the analyst towards the worst-modeled datapoints and providing hints for improvement. More inspiration could be borrowed from the GAN literature, such as “minibatch discrimination”—as demonstrated above, the random forests only see one data point at a time, but in training GANs, it has proven useful to instead examine multiple datapoints at a time to encourage the generator to learn how to generate a wide variety of datapoints rather than modeling a few datapoints extremely well; a ML model which can predict multiple outputs simultaneously based on multiple inputs would be analogous (that is, instead of X ~ A + B + C, it would look more like X1 + X2 + X3 ... ~ A1 + B1 + C1 + A2 + B2 + C2 + ..., with the independent & dependent variables from multiple data points all fed in simultaneously as a single sample) and might be an even more effective model critic.
Proportion of Important Thinkers by Global Region Over Time in Charles Murray’s Human Accomplishment
Human Accomplishment is a 200322ya book by Charles Murray reporting a large-scale citation analysis of biographical dictionaries & reference books on art/literature/science/mathematics/philosophy/science throughout history, quantifying the relative importance of “significant individuals” such as Isaac Newton or Immanuel Kant or Confucius and the temporal & geographical patterns; in particular, it demonstrates large European contributions throughout history and increasingly dramatically post-1400 AD. The dataset has been released.
Emil Kirkegaard created a visualization of of the proportion by rough geographic region (European/Asian/other) in R using ggplot2 and LOESS smoothing. Perhaps the most striking aspect of it is the Dark Ages showing up as a spike in Asian proportion, followed by the Great Divergence.
This visualization has been criticized as Eurocentrically-misleading and driven by artifacts in the analysis/graphing:
LOESS ignores the constraint that proportions must be 0-1 and naively extrapolates beyond the boundaries, producing negative estimates for some regions/times
no visualization of uncertainty is provided, either in the form of graphing the raw data points by superimposing a scatterplot or by providing standard errors or credible intervals. It is possible that the overall shapes or specific periods are no more than chance scatters in a time-series based on few datapoints.
LOESS can provide estimate local standard errors & confidence intervals but they are of questionable meaning in the absence of the underlying counts
alternatively, the distribution of significant figures may not be treated correctly parametrically
proportions may reflect a time-series with trends and so precision is exaggerated
None of these objections hold any water as the dataset and its embedded differences are sufficiently large that the method of analysis will make little difference; I will demonstrate this below by re-analyzing it to address the quibbles and show that all patterns remain intact or are sharpened. The above criticisms can be addressed by:
switching from a LOESS plot to splines or local binomial regressions
plotting the raw proportions grouped by decade or century
using a nonparametric bootstrap to calculate confidence intervals, a procedure which lends itself to visualization as an animation of plots of all the resamples, giving an intuitive sense of how important sampling error is to the overall pattern of curves and specific parts of history
alternately, instead of attempting to fit the proportion, one can fit the original count of significant figures in a binomial or log-normal Bayesian time-series model and sample from the posterior estimates of each region for each decade/century, and calculate posterior proportions, gaining full quantification of uncertainty, incorporation of any autocorrelation, and smoothing; no additional algorithms or theorems are required, demonstrating the elegance of Bayesian approaches
I didn’t realize Kirkegaard’s R code was available so I wound up redoing it myself (and getting the same results):
## export CSV from spreadsheet in https://osf.io/z9cnk/
h <- read.csv("HA.csv", header=TRUE)
summary(h)
# Serial Name Fl Birth Death Inventory ScienceField
# Min. : 11.00 Descartes, René : 4 Min. :-700.000 Min. :-640.000 Min. :-559.00 Science :1442 :2560
# 1st Qu.: 6144.50 Hooke, Robert : 4 1st Qu.:1557.250 1st Qu.:1580.000 1st Qu.:1638.00 Lit.West : 835 Tech : 239
# Median :12534.50 Leonardo da Vinci: 4 Median :1804.000 Median :1782.000 Median :1844.00 Music.West: 522 Phys : 218
# Mean :15994.27 Archimedes : 3 Mean :1585.638 Mean :1616.174 Mean :1682.81 Art.West : 479 Chem : 204
# 3rd Qu.:21999.75 Bacon, Francis : 3 3rd Qu.:1900.000 3rd Qu.:1863.000 3rd Qu.:1930.00 Phil.West : 155 Biol : 193
# Max. :43134.00 d'Alembert, Jean : 3 Max. :1949.000 Max. :1910.000 Max. :1997.00 Art.China : 111 Math : 191
# (Other) :3981 NA's :304 NA's :351 (Other) : 458 (Other): 397
# Index Duplicate BirthCountry WorkCountry Ethnicity Woman No..of.Inventories
# Min. : 0.60000 Min. :0.00000000 France : 564 France : 605 Germanic: 592 Min. :0.00000000 Min. :2.000000
# 1st Qu.: 3.54000 1st Qu.:0.00000000 Germany: 556 Britain: 574 French : 565 1st Qu.:0.00000000 1st Qu.:2.000000
# Median : 7.60000 Median :0.00000000 Britain: 554 Germany: 525 English : 441 Median :0.00000000 Median :2.000000
# Mean : 12.95713 Mean :0.06221889 Italy : 400 Italy : 406 Italian : 397 Mean :0.02198901 Mean :2.228916
# 3rd Qu.: 15.89000 3rd Qu.:0.00000000 USA : 306 USA : 375 USA : 276 3rd Qu.:0.00000000 3rd Qu.:2.000000
# Max. :100.00000 Max. :1.00000000 China : 239 China : 239 Chinese : 240 Max. :1.00000000 Max. :4.000000
# NA's :115 (Other):1383 (Other):1278 (Other) :1491 NA's :3753
levels(h$Ethnicity)
# [1] "Ancient Greek" "Ancient Roman" "Arabic" "Australian" "Basque" "Black" "Bulgarian" "Canadian"
# [9] "Chinese" "Croatian" "Czech" "Danish" "Dutch" "English" "Estonian" "Finnish"
# [17] "Flemish" "French" "Germanic" "Greek" "Hungarian" "Icelandic" "Indian" "Irish"
# [25] "Italian" "Japanese" "Jewish" "Latino" "New Zealand" "Norwegian" "Polish" "Portuguese"
# [33] "Romanian" "Scots" "Slavic" "Slovenian" "Spanish" "Swedish" "Swiss" "USA"
european <- c("Ancient Greek", "Ancient Roman", "Australian", "Basque", "Bulgarian", "Canadian", "Croatian", "Czech", "Danish",
"Dutch", "English", "Estonian", "Finnish", "Flemish", "French", "Germanic", "Greek", "Hungarian", "Icelandic", "Irish",
"Italian", "Jewish", "New Zealand", "Norwegian", "Polish", "Portuguese", "Romanian", "Scots", "Slavic", "Slovenian",
"Spanish", "Swedish", "Swiss", "USA")
asian <- c("Chinese", "Indian", "Japanese")
other <- c("Arabic", "Black", "Latino")
groupMembership <- function(e) { if (e %in% european) { "European" } else { if (e %in% asian) { "Asian" } else { "Other" } } }
h$Group <- as.factor(sapply(h$Ethnicity, groupMembership))
summary(h$Group)
# Asian European Other
# 507 3379 116
## We use 'Fl' (floruit/flourished), when a person is believed to have done their most important work,
## since birth/death is often unavailable.
## group to decades by rounding:
h$Fl.decade <- round(h$Fl, digits=-1)
hd <- subset(select=c(Fl.decade, Group), h)
hdcount <- aggregate(cbind(Group) ~ Fl.decade+Group, length, data=hd)
colnames(hdcount)[3] <- "Count"
## sort by time:
hdcount <- hdcount[order(hdcount$Fl.decade),]
nrow(h); sum(hdcount$Count)
# [1] 4002
# [1] 4002
head(hdcount, n=20)
# Fl.decade Group Count
# 178 -700 European 3
# 179 -680 European 1
# 180 -650 European 1
# 1 -600 Asian 2
# 181 -600 European 2
# 182 -580 European 2
# 183 -570 European 2
# 2 -550 Asian 1
# 184 -550 European 1
# 185 -540 European 5
# 3 -520 Asian 1
# 186 -520 European 3
# 4 -510 Asian 1
# 187 -510 European 2
# 188 -500 European 2
# 189 -480 European 6
# 190 -460 European 3
# 191 -450 European 7
# 5 -440 Asian 1
# 192 -440 European 11
## One issue with the count data: decades with zero significant figures from a group
## (which happens frequently) get suppressed. Some tools can handle the omission
## automatically but many cannot, so we need to manually insert any missing decades with '0'
decades <- seq(-700, 1950, by=10)
for (i in 1:length(decades)) {
d <- decades[i]
if (nrow(hdcount[hdcount$Fl.decade==d & hdcount$Group=="European",])==0) {
hdcount <- rbind(hdcount, data.frame(Fl.decade=d, Group="European", Count=0))}
if (nrow(hdcount[hdcount$Fl.decade==d & hdcount$Group=="Asian",])==0) {
hdcount <- rbind(hdcount, data.frame(Fl.decade=d, Group="Asian", Count=0))}
if (nrow(hdcount[hdcount$Fl.decade==d & hdcount$Group=="Other",])==0) {
hdcount <- rbind(hdcount, data.frame(Fl.decade=d, Group="Other", Count=0))}
}
hdcount <- hdcount[order(hdcount$Fl.decade),]
library(ggplot2); library(gridExtra)
c1 <- with(hdcount, qplot(Fl.decade, Count, color=Group) + stat_smooth())
c2 <- with(hdcount, qplot(Fl.decade, log1p(Count), color=Group) + stat_smooth())
grid.arrange(c1, c2, ncol=1)The absolute growth in human population and hence accomplishment post-1400 is so dramatic that it obscures earlier temporal variations:
Counts of “significant figures” in Human Accomplishment (2003) by geographic region, raw and log-transformed
Log-transformed, we can still see the inverted-V shape of European counts, but it’s somewhat subtle because it’s still being squashed by post-1400 increases and does leave room for doubt about sampling error. Moving on to reproducing the proportions plot:
## Create proportions by summing per decade, then looping over each group & dividing by total for that decade:
decadeTotals <- aggregate(Count ~ Fl.decade, sum, data=hdcount)
for (i in 1:nrow(hdcount)) {
total <- decadeTotals[decadeTotals$Fl.decade == hdcount[i,]$Fl.decade,]$Count
p <- hdcount[i,]$Count / total
hdcount$Proportion[i] <- if(is.nan(p)) { 0 } else { p }
hdcount$Total[i] <- total
}
with(hdcount, qplot(Fl.decade, Proportion, color=Group) + stat_smooth() + coord_cartesian(ylim = c(0, 1)))
Relative proportions of “significant figures” in Human Accomplishment (2003) by geographic region, LOESS-smoothed
We successfully reproduce it, modulo the LOESS standard errors (which can be disabled by adding se=FALSE to stat_smooth()), including the unwanted nonsensical extrapolations. It is possible with some tricky ggplot2 functionality to add in binomial smoothing (along with some jitter to unbunch the datapoints at the modal 0).
## roughly equivalent to:
# glm(cbind(Count,Total) ~ splines::ns(Fl.decade,3), family="binomial", data=hdcount, subset=Group=="European")
binomial_smooth <- function(...) { geom_smooth(se=FALSE, method = "glm", method.args = list(family = "binomial"), ...) }
with(hdcount, qplot(Fl.decade, Proportion, color=Group) +
binomial_smooth(formula = y ~ splines::ns(x, 3)) +
geom_jitter(aes(color=Group), width=0.013, height=0.013))
Relative proportions of “significant figures” in Human Accomplishment (2003) by geographic region, binomial-spline-smoothed for sensible extrapolation
This still doesn’t provide any indication of sampling error uncertainty, however. Kirkegaard provides one with CIs derived from bootstrapping, so I will provide something a little different: visualizing the uncertainty dynamically by graphing the smoothed proportions for each resample in an animation of hundreds of bootstrap samples.
So to do this bootstrap, we package up the various transformations from before, so we can sample-with-replacement the original dataset9, transform, and plot repeatedly:
transformAndProportion <- function(df) {
df$Fl.decade <- round(df$Fl, digits=-1)
dfd <- subset(select=c(Fl.decade, Group), df)
dfdcount <- aggregate(cbind(Group) ~ Fl.decade+Group, length, data=dfd)
colnames(dfdcount)[3] <- "Count"
decades <- seq(-700, 1950, by=10)
for (i in 1:length(decades)) {
d <- decades[i]
if (nrow(dfdcount[dfdcount$Fl.decade==d & dfdcount$Group=="European",])==0) {
dfdcount <- rbind(dfdcount, data.frame(Fl.decade=d, Group="European", Count=0))}
if (nrow(dfdcount[dfdcount$Fl.decade==d & dfdcount$Group=="Asian",])==0) {
dfdcount <- rbind(dfdcount, data.frame(Fl.decade=d, Group="Asian", Count=0))}
if (nrow(dfdcount[dfdcount$Fl.decade==d & dfdcount$Group=="Other",])==0) {
dfdcount <- rbind(dfdcount, data.frame(Fl.decade=d, Group="Other", Count=0))}
}
dfdcount <- dfdcount[order(dfdcount$Fl.decade),]
decadeTotals <- aggregate(Count ~ Fl.decade, sum, data=dfdcount)
for (i in 1:nrow(dfdcount)) {
p <- dfdcount[i,]$Count / decadeTotals[decadeTotals$Fl.decade == dfdcount[i,]$Fl.decade,]$Count
dfdcount$Proportion[i] <- if(is.nan(p)) { 0 } else { p }
}
return(dfdcount)
}
bootPlot <- function(df) {
n <- nrow(df)
bootDf <- df[sample(1:n, n, replace=TRUE),]
bootDfdcount <- transformAndProportion(bootDf)
## WARNING: can't just call qplot due to old 'animation'/ggplot2 bug; have to assign & 'print'
p <- with(bootDfdcount, qplot(Fl.decade, Proportion, color=Group) +
binomial_smooth(formula = y ~ splines::ns(x, 3)) +
geom_jitter(aes(color=Group), width=0.013, height=0.013))
print(p)
}
library(animation)
saveGIF({for (i in 1:200) { bootPlot(h) }}, interval=0.15, ani.width=1300, ani.height=700,
movie.name="2003-murray-humanaccomplishment-region-proportions-bootstrap.gif", clean=FALSE)Animation of repeatedly resampling & plotting relative proportions of “significant figures” in Human Accomplishment (Murray 2003) by geographic region, demonstrating effects of sampling error on proportions & historical curves
The bootstrap animation suggests to me that while the very earliest time-periods are opaque and the Dark Ages difference between Europe & Asia may be somewhat higher or lower, the overall shape doesn’t change meaningfully.
The time-series aspect of the data on visual inspection appears to be a simple auto-regressive model with a drift upwards, low-order models like ARIMA(1,1,0), ARIMA(1,1,2), or ARIMA(0,1,2); this is probably due to the world population steadily increasing while the per capita rates remain stable.
library(forecast)
efit <- auto.arima(subset(hdcount, select=c("Fl.decade", "Count"), Group=="European")$Count)
afit <- auto.arima(subset(hdcount, select=c("Fl.decade", "Count"), Group=="Asian")$Count)
ofit <- auto.arima(subset(hdcount, select=c("Fl.decade", "Count"), Group=="Other")$Count)
par(mfrow=c(3,1))
plot(forecast(efit), ylim=c(0,200)); axis(side=1, labels=decades, at=seq(1, length(decades)))
plot(forecast(afit), ylim=c(0,200)); axis(side=1, labels=decades, at=seq(1, length(decades)))
plot(forecast(ofit), ylim=c(0,200)); axis(side=1, labels=decades, at=seq(1, length(decades)))
Simple ARIMA time-series fits & forecasts to 3 global regions of “significant figures” in Human Accomplishment
We can combine the sampling error quantification of full Bayesian posteriors, Poisson distribution of counts, and time-series aspects into a single Bayesian model using brms as a convenient interface to Stan (rather than writing out the full model by hand), with uninformative priors, and then visualize the posterior distribution of the proportions (which itself is simply a transformation of the posterior):
library(brms)
b <- brm(Count ~ (1|Group), autocor = cor_bsts(~ Fl.decade | Group), family="zero_inflated_poisson", data = hdcount)
## Rather than use `fitted` to get the 95% CI & compute proportion, it would also be possible to draw samples from
## the posterior for each group/decade, total, calculate per-group proportion, and then summarize into quantiles; but
## that is much slower and requires more finicky code:
posterior <- fitted(b)
hdcount$B.low.prop <- posterior[,3] / hdcount$Total
hdcount$B.mean.prop <- posterior[,1] / hdcount$Total
hdcount$B.high.prop <- pmin(1, posterior[,4] / hdcount$Total)
predframe <- subset(hdcount, select=c("B.low.prop", "B.high.prop"))
with(hdcount, ggplot(hdcount, aes(Fl.decade, Proportion, color=Group)) +
geom_point() +
geom_line(data=predframe) +
geom_ribbon(aes(ymin=B.low.prop, ymax=B.high.prop), alpha=0.05, data=predframe))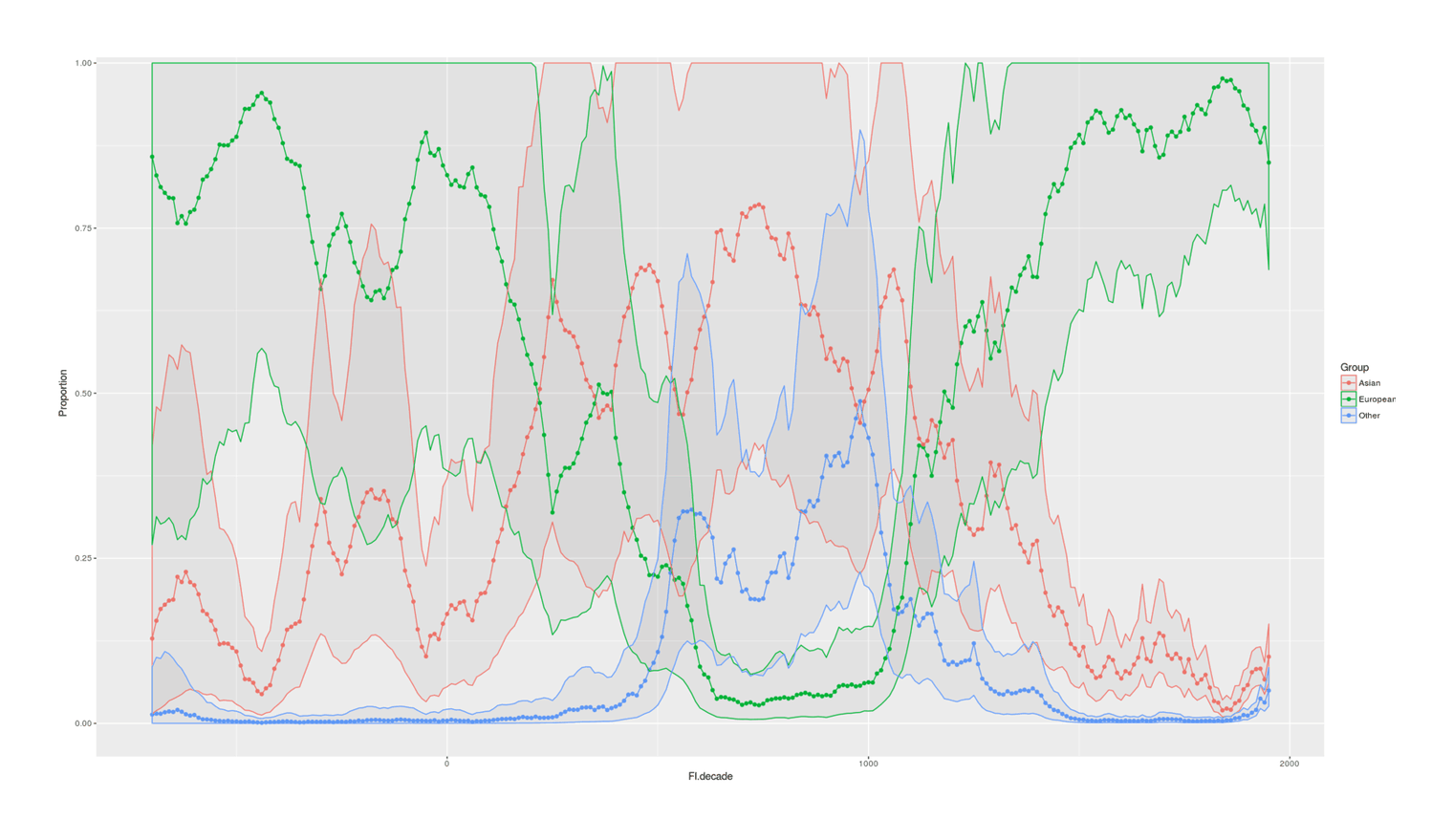
Bayesian multi-level time-series of “significant figures”; shaded region indicates 95% credible interval around group mean in that decade
The smoothed time-series looks about the same, and the CIs suggest, like the bootstrap, that there is great uncertainty early on when populations are small & surviving figures are rare, but that the dark ages dip looks real and the European increases in proportion since then are also highly probable.
So overall, correcting for the infelicities in Kirkegaard’s original graph makes the graph somewhat cleaner and is helpful in providing quantification of uncertainty, but none of the problems drove the overall appearance of the curve in the slightest bit. If the graph is wrong, the issues will lie in systematic biases in the data itself—not statistical quibbling over sampling error or LOESS curves crossing an axis. (Comparison with graphs drawn from other cliometric datasets such as Wikipedia or particularly Seshat would be informative.)
Program for Non-Spaced-Repetition Review of past Written Materials for Serendipity & Rediscovery: Archive Revisiter
“Spaced repetition” helps one remember facts by creating discrete flashcards which one tests oneself on at increasingly distant ‘spaced’ time periods, repeating the fact just before one probably would have forgotten it; using software to track & automate tests & review scheduling, spaced repetition can scale to hundreds of thousands of discrete items.
If spacing out facts can help one remember by repeating items just before they are forgotten, is there any use for an “anti-spaced repetition” with the opposite method of repeating items only after they are probably forgotten?
I can think of two: first, it could be used to plan consumption of media such as movies by eg. tracking one’s favorite movies of all time and scheduling a rewatch whenever one is predicted to have forgotten enough to make them novel & highly enjoyable again. Second, and more interestingly, it could be used as a serendipity generator by allowing efficient processing of notes or excerpts or old writings.
In rereading such materials many years later, one often gains a new perspective or learns something useful because one forgot something: one didn’t understand something about it at the time, or new material has radically changed one’s interpretation, and since it’d been forgotten, no use could be made of it. Unfortunately, using spaced repetition to memorize such material, while ensuring any serendipitous connections get made as soon as possible, would be radically infeasible for bulky items (a single lengthy text excerpt might correspond to hundreds of discrete items, quickly overloading even SRS systems) and for almost all items, useless. One can justify rereading old material once or perhaps twice, but not many rereads nor full memorization. But rereading haphazardly is likely to inefficiently cover some material many times while neglecting others, and such rereads will often be far too early in time (or—a lesser concern here—too late).
Instead of spaced repetition, one would instead use anti-spaced repetition: each item would be tracked and reviewed and its expected forgetting time predicted, as in spaced repetition, but instead of scheduling a review before forgetting, a review is scheduled for some time (probably long afterwards) after forgetting. The total number of reviews of each item per user lifetime would be set to a small number, perhaps 1–4, bounding the time consumption at a feasible amount.
Such an anti-spaced repetition system could be used with hundreds of thousands of notes or clippings which a person might accumulate over a lifetime, and enable them to invest a few minutes a day into reading old notes, occasionally coming up with new insights, while ensuring they don’t waste time reading notes too many times or reading notes they likely already remember & have exhausted.
One reason to take notes/clippings and leave comments in stimulating discussions is to later benefit by having references & citations at hand, and gradually build up an idea from disparate threads and make new connections between them. For this purpose, I make extensive excerpts from web pages & documents I read into my Evernote clippings (functioning as a commonplace book), and I comment constantly on Reddit/LessWrong/HN etc. While expensive in time & effort, I often go back, months or years later, and search for a particular thing and expand & integrate it into another writing or expand it out to an entire essay of its own. (I also value highly not being in the situation where I believe something but I do not know why I believe it other than the conviction “I read it somewhere, once”.) One might also want to revisit many other things, which are currently hard to revisit in any systematic way: project or technology ideas, family photos, leisure activities (favorite movies, games, recipes, clothes, vacation spots)…
This sort of personal information management using simple personal information managers like Evernote works well enough when I have a clear memory of what the citation/factoid was, perhaps because it was so memorable, or when the citations or comments are in a nice cluster (perhaps because there was a key phrase in them or I kept going back & expanding a comment), but it loses out on key benefits to this procedure: serendipity and perspective.
As time passes, one may realize the importance of an odd tidbit or have utterly forgotten something or events considerably changed its meaning; in this case, you would benefit from revisiting & rereading that old bit & experiencing an “aha!” moment, but you don’t realize it. So one thing you could do is reread all your old clippings & comments, appraising them for reuse.
But how often? And it’s a pain to do so. And how do you keep track of which you’ve already read? One thing I do for my emails is semi-annually I (try to) read through my previous 6 months of email to see what might need to be followed up on10 or mined for inclusion in an article. (For example, an ignored request for data, or a discussion of darknet markets with a journalist I could excerpt into one of my DNM articles so I can point future journalists at that instead.) This is already difficult, and it would be even harder to expand. I have read through my LessWrong comment history… once. Years ago. It would be more difficult now. (And it would be impossible to read through my Reddit comments as the interface only goes back ~1000 comments.)
Simply re-reading periodically in big blocks may work but is suboptimal: there is no interface easily set up to reread them in small chunks over time, no constraints which avoid far too many reads, nor is there any way to remove individual items which you are certain need never be reviewed again. Reviewing is useful but can be an indefinite timesink. (My sent emails are not too hard to review in 6-month chunks, but my IRC logs are bad—7,182,361 words in one channel alone—and my >38k Evernote clippings are worse; any lifestreaming will exacerbate the problem by orders of magnitude.) This is probably one reason that people who keep journals or diaries don’t reread Nor can it be crowdsourced or done by simply ranking comments by public upvotes (in the case of Reddit/LW/HN comments), because the most popular comments are ones you likely remember well & have already used up, and the oddities & serendipities you are hoping for are likely unrecognizable to outsiders.
This suggests some sort of reviewing framework where one systematically reviews old items (sent emails, comments, IRC logs by oneself), putting in a constant amount of time regularly and using some sort of ever expanding interval between re-reads as an item becomes exhausted & ever more likely to not be helpful. Similar to the logarithmically-bounded number of backups required for indefinite survival of data (2012), “Deconstructing Deathism—Answering Objections to Immortality”, Mike 2004 (note: this is an entirely different kind of problem than those considered in Freeman Dyson’s immortal intelligences in Infinite in All Directions, which are more fundamental), discusses something like what I have in mind in terms of an immortal agent trying to review its memories & maintain a sense of continuity, pointing out that if time is allocated correctly, it will not consume 100% of the agent’s time but can be set to consume some bounded fraction:
It seems reasonable that past versions of the self would “survive” as we remember the events of times past, that is to say, our episodic memories, and this would have importance in our continuing to persist as what could be considered the “same” albeit also a changing, developing person. But in addition to this mnemonic reinforcement I imagine there would be a more general feeling of being a particular individual, an “ambiance” derived from but not referring to any specific past experiences. Ambiance alone would not be sufficient, I think, to make us who we are; episodic memories would also be necessary, yet it could considerably lessen the need for frequent recall and thus alleviate the problem of dilution.
Another interesting thought is that certain items might consistently be consulted more frequently than others. (Indeed, would this not be expected?) In this way it would actually be possible to bypass the dilution effect and instead allow a fixed fraction of time for perusal of any given item, even as more items were added indefinitely. A simple way of doing this could be first to allow some fixed fraction of the time for day-to-day affairs and other non-archival work (“prime time”), and spend the rest of the time on perusal of personal archives (“archive time”). The exact apportioning of prime versus archive time is not important here, but it will be instructive to consider how the archive time itself might be subdivided. A simple, if overly simplistic, strategy would be to have half this time devoted to the first century’s records, half the remainder to the second century, and so on. (Since there would only be a finite number of centuries, there would be some unused archive time at the end, which could be spent as desired. Note, however, that in the limit of infinite total time covering infinitely many centuries, the usage of archive time would approach but not exceed 100%.) In this way, then, there would be a fixed fraction of archive time, 2 − n, spent on the nth century’s records, regardless of how many centuries beyond the nth were lived or how many records accumulated. True, this way of apportioning time might not be much good beyond a few centuries; only about one trillionth the total time would be spent on the 40th century, for instance, around 1⁄300 sec per 100 years. (Possibly a lot could be covered even in this brief interval of about 3 million nanoseconds, however.) But the apportionment scheme could be adjusted.
A more interesting and plausible, if slightly harder-to-describe scheme would be to choose a constant c > 0 and allow the fraction to the nth-century records. It is easy to show that the time for all centuries will add up to 100% as before, whatever positive value of c we start with. Starting with c = 10 will get 10% of the total time spent on the first century, with subsequent centuries receiving a diminishing share as before, but the rate of falloff will be much slower, so that the 40th century will still receive 0.4%, or about 5 months per 100 years, that is to say, 240 million nanoseconds per minute. If we suppose that our immortal settles eventually into a routine in which 10% of the time overall is archive time, there would be 24 million nanoseconds available each minute of life for the 40th century’s memories alone, if desired, with many other centuries getting more or less comparable or greater amounts of attention, and none omitted entirely. This, I think, makes at least a plausible case that a reasonable sense of one’s personal identity could be sustained indefinitely.
In the above examples the greatest proportion of archive time falls to the earlier records, which might be fitting since these should be the most important as formative years for the prospective immortal, thus the most important for identity maintenance. (Memory recall would also naturally occur during prime time; the emphasis here could be on recent events, to maintain a balance overall.) In summary, then, we have considered ways that the problem of dilution might be successfully managed. Relatively infrequent perusal of memories might still suffice to maintain the necessary continuity with past versions of the self, or proper scheduling could stabilize the frequency of recall and bypass the dilution effect, or both. We see in any case that the problem is not what it may seem at first sight. We have no guarantee, of course, that it would not get out of bounds, but certainly some grounds for hope.
So you could imagine some sort of software along the lines of spaced repetition systems like Anki/Mnemosyne/Supermemo which you spend, say, 10 minutes a day at, simply rereading a selection of old emails you sent, lines from IRC with n lines of surrounding context, Reddit & LW comments etc; with an appropriate backoff & time-curve, you would reread each item maybe 3 times in your lifetime (eg. first after a delay of a month, then a year or two, then decades). Each item could come with a rating function where the user rates it as an important or odd-seeming or incomplete item and to be exposed again in a few years, or as totally irrelevant and not to be shown again—as for many bits of idle chit-chat, mundane emails, or intemperate comments is not an instant too soon! (More positively, anything already incorporated into an essay or otherwise reused likely doesn’t need to be resurfaced.) This could also be implemented in a personal wiki or knowledge graph like Org Mode, where views are tracked and implicitly counted, and items are ‘suggested’ based on age (Paul Bricman calls such a resurfacing system “antimemories”).
This wouldn’t be the same as a spaced repetition system which is designed to recall an item as many times as necessary, at the brink of forgetting, to ensure you memorize it; in this case, the forgetting curve & memorization are irrelevant and indeed, the priority here is to try to eliminate as many irrelevant or useless items as possible from showing up again so that the review doesn’t waste time.
More specifically, you could imagine an interface somewhat like Mutt which reads in a list of email files (my local POP email archives downloaded from Gmail with getmail4, filename IDs), chunks of IRC dialogue (a grep of my IRC logs producing lines written by me ±10 lines for context, hashes for ID), LW/Reddit comments downloaded by either scraping or API via the BigQuery copy up to 2015, and stores IDs, review dates, and scores in a database. One would use it much like a SRS system, reading individual items for 10 or 20 minutes, and rating them, say, upvote (‘this could be useful someday, show me this ahead of schedule in the future’) / downvote (push this far off into the future) / delete (never show again). Items would appear on an expanding schedule. For example if one wanted to review items 4 times over the next 50 years (roughly my life expectancy), a schedule might be:
round({t=0:4; t^6.981})
# [1] 0 1 126 2142 15958So in 1 day, then a third of a year, then after 5.8 years, then after 43 years. Alternately, a geometric series might be a bit kinder and not too front-loaded:
review <- function(n, r, a) { a * (1 - r^n) / (1 - r) }
reviews <- function(n, r, a) { sapply(1:n, function(nn) { review(nn, r, a) }) }
findR <- function (firstReview=31, n_total=3, years=50) { optimize(interval=c(0, 1000),
f = function(r) { abs(sum(sapply(1:n_total,
function(n){review(n, a=firstReview, r=r)})) - (365*years)) })$minimum }
findR(firstReview=30, n_total=4, years=50)
# [1] 7.728823216
round(reviews(4, 7.728823216, 30))
# [1] 30 262 2054 15904The geometric series allows for easy incorporation of rating modifications: a downvote penalty might multiply r by 1.5, vs 0.5 for upvotes. This would also allow some input from statistical algorithms which predict upvote/downvote/delete and advances/delays items based on that, which would hopefully quickly learn to avoid idle chit-chat and short performative utterances and start to prioritize more interesting & unusual items. (For example, a good start might be a SVM on a bag-of-words version of each item’s text, and then as the dataset ratings expand, more complicated algorithms could be plugged in.)
As far as I know, some to-do/self-help systems have something like a periodic review of past stuff, and as I mentioned, spaced repetition systems do something somewhat similar to this idea of exponential revisits, but there’s nothing like this at the moment.
On the Value of New Statistical Methods
Genetic correlation research is a hot area in 2016–2017: my WP article passed 400 references in May 2017. What is particularly interesting reference-wise is that publications 2015–2017 make up around half of the results: so more genetic correlations calculated in the past 3 years than in the previous 80 years since first estimates were made somewhere in the 1930s or so.
For calculating them, there are 3 main methods.
twin registry studies require twin phenotypic measurements which can usually be collected by mailed surveys and to analyze them one computes some Pearson’s r or uses a standard SEM with additional covariance paths (doable with Wright’s path analysis back in the 1930s by hand), scaling roughly linearly with sample size, having excellent statistical power at a few hundred twin pairs and capturing full heritabilities
for GCTA, one requires full raw SNP data on 5000+ unrelated individuals at $100+ a sample, along with simultaneous phenotypic measurements of both traits and must use complicated custom software whose computation scales exponentially and can only examine a narrow subset of heritability
for LDSC, one requires public summary polygenic scores but they can be from separate GWASes and calculated on traits individually, and the computational complexity is closer to linear than exponential; the penalty for not needing raw SNP data from twice-measured individuals is that SNP costs double or more since multiple GWASes are used, and LDSC even more inefficient than GCTA, so you’ll need >10,000 individuals used in each polygenic score, and still need custom software.
In other words, the twin method is old, simple, requires small sample sizes, and easily obtained phenotypic measurements; while GCTA/LDSC is new, complicated, and requires expensive novel genetic sequencing data in huge sample sizes as well as the phenotypic measurements. So naturally LDSC gets used an order of magnitude more! Looking at the bibliography, we can guesstimate the rates at twin: 1 paper/year; GCTA (requiring raw data), 10/year; LDSC (public summary stats), 100/year.
Amazing the difference methods can make. It’s all about data access. For all its disadvantages, LDSC statistically works around the lack of individual-level raw data and makes do with the data that gets publicly released because it is not seen to violate ‘privacy’ or ‘bioethics’, so any researcher can make use of the method on their particular dataset, while twin and GCTA require individual-level data which is jealously guarded by the owners.
Methodologists and statisticians are probably seriously undervalued: a good new method can cause a revolution.
Bayesian Power Analysis: Probability of Exact Replication
Psychologist Michael Kane mentions:
TFW a correlation of interest in a new study (n = 355) replicates that from a prior study (n = 182) to the second decimal (r = 0.23). Winning!
Turning up the same correlation twice is somewhat surprising because random sampling error will vary substantially the empirical correlation r̂ from sample to sample, as reflected by the wide credible intervals around r with n = 182-355. How surprising is it? Is it “too good to be true”?
One approach would be to ask, if we generated bivariate samples of size n = 355 with a fixed relationship of r = 0.23, how often would the samples generate a rounded estimate of r̂ = 0.23?
set.seed(2017-07-28)
library('MASS')
powerSim <- function (r_gen, n, r_test=NA) {
data <- mvrnorm(n=n, mu=c(0, 0), Sigma=matrix(c(1, r_gen, r_gen, 1), nrow=2))
r_est = cor.test(data[,1], data[,2])$estimate
if (is.na(r_test)) { r_test <- r_gen }
return(round(r_test, digits=2) == round(r_est, digits=2))
}
powerSims <- function(r, n, r_test=NA, iters=100000) {
sim <- replicate(iters, powerSim(r,n, r_test=r_test))
return(sum(sim) / length(sim))
}
powerSims(0.23, 355)
# [1] 0.07798So around 8% of the samples.
This treats r̂ = r = 0.23 as a parameter known with infinite precision, rather than an estimate r̂ (using around half the data) of the unknown parameter r; there would be considerable posterior uncertainty about what r is, and this will affect how often two samples would yield the same estimate—if the true r was, say, 0.10 (as is entirely possible), it would be highly unlikely for the second sample to yield r̂ = 0.23 again, because the overestimation fluke would have to repeat itself twice to yield both r̂ = 0.23.
To incorporate the uncertainty, we can feed in a simulated dataset exactly matching the description of n = 182 & r = 0.23 to an uninformative Bayesian model, calculate a posterior distribution over r (which gives CIs of 0.09–0.37), and then draw from the posterior possible rs and run the original simulation asking how often we recover r̂ = 0.23.
library(brms)
n1 = 182
n2 = 355
r1 = 0.23
data1 = mvrnorm(n=n1, mu=c(0, 0), Sigma=matrix(c(1, r1, r1, 1), nrow=2), empirical=TRUE)
colnames(data1) <- c("x", "y")
b1 <- brm(y ~ x, iter=20000, data=data1); summary(b1)
# ...Population-Level Effects:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# Intercept 0.00 0.07 -0.14 0.14 40000 1
# x 0.23 0.07 0.09 0.37 40000 1
posteriorX <- fixef(b1, summary=FALSE)[,2]; summary(posteriorX)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -0.08060884 0.18061570 0.23010870 0.22999820 0.27916800 0.55868700
replicates <- sapply(posteriorX, function(r_post) { powerSim(r_post, n2, r_test=r1) })
summary(replicates); mean(replicates)
# Mode FALSE TRUE NA's
# logical 38262 1738 0
# [1] 0.04345Around 4% of the time, reflecting the increased improbability of true values like r = 0.09 or r = 0.37 producing the specific sample estimate of r̂ = 0.23.
Thus, observing the same summary statistics in even relatively large samples is somewhat suspicious and might be a good reason to double-check other aspects of the code & data.
Expectations Are Not Expected Deviations and Large Number of Variables Are Not Large Samples
If one has a large number of variables with a certain expectation, it is tempting to interpret the expectation or central limit theorem or law of large numbers as implying that the sum of a large number of variables or after a large number of timesteps, the observed sample value will be close or identical to the expected value. So for coin-flipping, one knows that flipping 10 coins could easily yield a large deviation like a sum of 9 heads instead of the expected 5 heads, but one then thinks that after a million coin flips, the sum of heads will probably be 500,000. Another example of this mistake might be to make arguments about scientific research or charities: “charitable intervention X is affected by hundreds or thousands of different variables and the benefits or costs unfold over long time periods like decades or centuries; our best estimate of the mean value of interventions like X is that it is some small value Y; thus, by CLT etc, we can be sure that X’s ultimate value will be neither much bigger nor much smaller than Y but very close to Y, and, particularly, we can be sure that there are no interventions like X which could possibly turn out to have ultimate values which are orders of magnitude larger or smaller than Y, so we can rule out any such claims and we know the Value of Information is small.”
This is not wrong so much as misunderstood: one might call it a confusion of the variable’s distribution with the sampling distribution. The value only becomes closer in a relative sense; in an absolute sense, as more variables are added—without the absolute magnitude of each shrinking linearly—the actual deviation from the expectation simply becomes larger and larger. (Like martingales: the expectation is the same as the current value, but the variance increases with time.)
As Wikipedia puts it in discussing how “diversification” works, it is a mistake to think that one ‘diversifies’ one’s investments by adding additional investments of the same size; for any variance reduction, the total investment must instead be split up among ever more different investments as many small investments:
In general, the presence of more assets in a portfolio leads to greater diversification benefits, as can be seen by considering portfolio variance as a function of n, the number of assets. For example, if all assets’ returns are mutually uncorrelated and have identical variances , portfolio variance is minimized by holding all assets in the equal proportions .[Samuelson, Paul, “General Proof that Diversification Pays”, Journal of Financial and Quantitative Analysis 2, March 196758ya, 1-13.] Then the portfolio return’s variance equals = = , which is monotonically decreasing in n.
The latter analysis can be adapted to show why adding uncorrelated volatile assets to a portfolio, [see Samuelson, Paul, “Risk and uncertainty: A fallacy of large numbers”, Scientia 98, 196362ya, 108-113.] [Ross, Stephen, “Adding risks: Samuelson’s fallacy of large numbers revisited”, Journal of Financial and Quantitative Analysis 34, September 199926ya, 323-339.] thereby increasing the portfolio’s size, is not diversification, which involves subdividing the portfolio among many smaller investments. In the case of adding investments, the portfolio’s return is instead of and the variance of the portfolio return if the assets are uncorrelated is which is increasing in n rather than decreasing. Thus, for example, when an insurance company adds more and more uncorrelated policies to its portfolio, this expansion does not itself represent diversification—the diversification occurs in the spreading of the insurance company’s risks over a large number of part-owners of the company.
1963 “Risk and uncertainty: A fallacy of large numbers” opens by recounting an anecdote:
Is it true that an insurance company reduces its risk by doubling the number of ships it insures?
…a few years ago I offered some lunch colleagues to bet each $200 to $100 that the side of a coin they specified would not appear at the first toss. One distinguished scholar—who lays no claim to advanced mathematical skills—gave the following answer:
I won’t bet because I would feel the $100 loss more than the $200 gain. But I’ll take you on if you promise to let me make 100 such bets.
What was behind this interesting answer? He, and many others, have given something like the following explanation. “One toss is not enough to make it reasonably sure that the law of averages will turn out in my favor. But in a hundred tosses of a coin, the law of large numbers will make it a darn good bet. I am, so to speak, virtually sure to come out ahead in such a sequence, and that is why I accept the sequence while rejecting the single toss.”
4. Maximum Loss And Probable Loss.—What are we to think about this answer?
…Firstly, when an insurance company doubles the number of ships it insures, it does also double the range of its possible losses or gains. (This does not deny that it reduces the probability of its losses.) If at the same time that it doubles the pool of its risks, it doubles the number of its owners, it has indeed left the maximum possible loss per owner unchanged; but—and this is the germ of truth in the expression “there is safety in numbers”—the insurance company has now succeeded in reducing the probability of each loss; the gain to each owner now becomes a more certain one.
In short, it is not so much by adding new risks as by subdividing risks among more people that insurance companies reduce the risk of each. To see this, do not double or change at all the original number of ships insured by the company: but let each owner sell half his shares to each new owner. Then the risk of loss to each owner per dollar now in the company will have indeed been reduced.
Undoubtedly this is what my colleague really had in mind. In refusing a bet of $100 against $200, he should not then have specified a sequence of 100 such bets. That is adding risks. He should have asked to subdivide the risk and asked for a sequence of 100 bets, each of which was 100th as big (or $1 against $2).
In the insurance example, ships do not change their insured value (your liability) simply because you insure more of them, and they certainly do not halve in value simply because you have decided to take more insurance. If a ship is worth $1m with an expected profit of $10k and a SD of profits of $5k, when you insure 1000 ships, your profit is distributed as , and when you double it, now the distribution is —absolute size of your fluctuations has increased, not decreased. As a percentage, it has gone down indeed, but the absolute size has still gone up. Similarly, by claiming to prefer an investment of 100 bets and putting not $200 but $20,000 at risk, the colleague has raised the stakes greatly, and if the prospect of fluctuations of $100 unsettled his stomach before, he will enjoy less the SD of ~$1,500 from the proposed 100 coinflips (95% quantiles of $2,000 to $,8000) and even a ~1% chance of a loss such as −$400; he has reduced the risk of any loss, yes, and most of the outcomes are indeed relatively closer to the expectation than with just 1 coinflip, but he has inadvertently replaced a small SD of $150 with the much larger one of $1,500, and of course, his worst case scenario has gotten much worse—with just one coin flip he could never have lost $400 or more, but now he can and occasionally would.
Another interesting example comes from Cavalli-1971 The Genetics of Human Populations, where he argues that a priori, differences between human races on complex traits (intelligence in this case), in the absence of selection, cannot exist solely based on the large number of genes contributing to them, by the law of large numbers:
In this context, it is worth mentioning that Jensen states that because the gene pools of whites and blacks are known to differ and “these genetic differences are manifested in virtually every anatomical, physiological, and biochemical comparison one can make between representative samples of identifiable racial groups” therefore “there is no reason to suppose that the brain should be exempt from this generalization.” There is, however, no reason why genes affecting IQ which differ in frequency in the gene pools of blacks and whites, should be such that, on the average, whites would have significantly higher frequencies of genes increasing IQ than would blacks. On the contrary, one should expect, assuming no tendency for high IQ genes to accumulate by selection in one or other race, that the more polymorphic genes there are that affect IQ and that differ in frequency in blacks and whites, the less likely it is that there is an average genetic difference in LQ between the races. This follows from that most basic law of statistics, the law of large numbers, which predicts increasing accuracy of a mean based on increasing numbers of observations (See Appendix I).
Cavalli-Sforza is correct to note that, unless we wish to make (still) very controversial claims about differing selection, there is no apparent reason for any intelligence-related allele to be systematically rarer in one population than another, although of course they will in practice differ slightly due to random chance (genetic drift, demographic bottlenecks etc), and that as this applies to all intelligence-related alleles, we would predict that the expectation of all populations to be identical. He, however, commits the fallacy of large numbers when he then interprets the law of large numbers as guaranteeing that all populations will be identical, while in fact, they will be different, and the absolute size of the differences will increase—not decrease—“the more polymorphic genes there are that affect IQ”. Like with diversification or insurance or coinflipping, the desired disappearance of the variance only happens if each random variable (investment, insured vessel, coinflip) decreases proportional to the total number of random variables; for Cavalli-Sforza’s argument to go through, it would need to be the case that every new IQ gene divvied up a fixed pie—but why would that be the case and how could that be known a priori? More pointedly, we could note that Cavalli-Sforza’s argument proves too much because it is equally applicable within races too, and implies that there could be no differences of important magnitude between humans of the same race on highly polygenic traits (and if someone wanted to try to rescue the argument by claiming we should expect mean differences or some sort of selection, then amend “humans of the same race” to “siblings in the same family”!). Cavalli-Sforza’s error is particularly striking since ch8 of the same book devotes extensive discussion, with many graphs, to how genetic drift will greatly differentiate populations over time, and takes pains to point out that the expectation of gene frequencies p is merely the expectation, and the actual frequency will diverge arbitrarily far in a random walk and over a long enough time (connected to the population size) will eventually reach fixation at either p = 1 or p = 0, and certainly not converge exactly on the original p.11 Indeed, given the a posteriori measured extent of average differences in allele frequency of ~0.12 and the assumption of no selection, Chuck flips Cavalli-Sforza’s argument on its head and points out that the standard genetic drift framework ( et al 2013) dating back to Wright implies that a difference of 0.12 yields large racial differences in polygenic traits! Clearly, Cavalli-Sforza’s argument does not prove what one would like it to.
The sum is not the mean: there is a difference between flipping 1 coin a thousand or a million times, the sum of a thousand or a million coins flipped 1 time, and the mean of a thousand or a million sums of a million coins; the distribution of the mean does indeed converge tightly, but the distribution of the sum just gets broader and broader. The expectation or mean is just the best estimate one can make over a large number of samples under a particular loss. But the long-run mean of many samples is not the same thing as the expected deviation of a single sample.
One might be dealing with something like a Cauchy distribution where there is not a mean in the first place. But more importantly, just because the expectation is a certain number like 0, doesn’t mean any specific realization will be 0, and indeed the expectation may actually be an impossible value. (Imagine a variable X which is the sum of an odd number of -1 or +1 variables; the expectation of this X is, of course, 0, however, one will never actually observe a sample of X to be 0, because the parity means there will always be a -1 or +1 ‘left over’ inside the sum and so X will always be either -1 or +1. To reach the expectation of 0, one would have to create many Xs and average them, and the more Xs one draws and averages, the closer the average will be to 0.)
For Gaussians, the single-sample sum of a set of Gaussian variables is the sum of their means with a variance equal to the sum of their variances (); if we sampled repeatedly and averaged, then we would indeed converge on the expected mean, but the expected deviation from the mean of a single sample is governed by the variance which can be extremely large. The increasing spread means that it would be extremely surprising to get exactly, or even near, the expectation. An example Monte Carlo of the sum of increasing numbers of 𝒩(0,1) deviates demonstrates the absolute deviation increases as we go from sum of 100 variables to 10,000 variables:
round(sapply(seq(100,10000,by=100), function(x) { mean(replicate(10000, abs(sum(rnorm(x))))) } ))
# [1] 8 11 14 16 18 20 21 23 24 25 26 27 29 30 31 32 33 34 35 35 37 38 38 39 40 41 41 42 43 44 45 45 46 46 47 48 48 49 50 50 51 52 52
# [44] 53 53 54 55 56 56 56 57 58 58 58 59 59 61 61 62 62 62 62 64 63 64 65 65 65 67 66 68 67 68 69 70 70 70 70 71 71 72 72 73 73 74 75
# [87] 74 75 75 75 76 76 77 78 78 78 78 80 80 80Or consider a 1D random walk. The best estimate one can make under total ignorance of where the walker is, is to guess, regardless of how many n steps it has made, that the walker is at the origin: 0. If we run many random walkers for n steps each and ask what the best prediction of the mean is, we would be right in saying it’s 0. We would not be right in saying that the walkers have not moved far or that we would expect them all to ‘converge’ and be at or at least very near 0. However, if one asks, what is the expected distance from the origin after n steps, the answer turns out to be ie. the more steps taken, the further we expect to find the walker, even if we cannot predict in what direction it has gone on average. Similarly, for a Gaussian random walk, we find that after n steps the walker will average a distance of from the origin (and possibly much further).
Further, should there be any absorbing states, we may find that our walkers will not be at their expectation but at the absorber—an example being Gambler’s ruin where repeatedly taking +EV bets can guarantee eventual $0/bankruptcy, or the infamous martingale where the expectation of each bet may be ~0 but the martingale player eventually is either bankrupt or profitable, never exactly even. Another analogy might be stock-picking: the expected value of each stock is about the same due to efficient markets, and if one indexes and waits a long time, one will likely get the fabled average return of ~7%; but if one buys a single individual stock and waits a long time, the return will likely be either -100% or >>7%.
In any process or scenario in which we are dealing with large numbers of variables which sum to produce a final result, even if each of those variables is neutral, a single sample will be potentially arbitrarily absolutely far from the expectation in a way which will surprise someone who believes that the law of large numbers ensures that the result must be extremely close to the expectation both relatively and absolutely.
Founder Effects
This observation about the size of deviations increases can also apply to collections of variables: suppose we have some highly dimensional datapoint with thousands of dimensions—like a human, where we are looking at overall traits like height, weight, personality, intelligence, preferences, every kind of disease and health variable, and so on. It is a commonplace of survey & experimental design to note that if we randomly sample humans, they will have an expected value of 0 on each trait, and by CLT, the more n we sample, the smaller the % expected deviation from that mean 0; this is why randomized experiments work (because all the confounding slowly goes away as they get balanced), and why small random surveys can measure the total population; this asymptotic logic is great for large samples, but at the small samples one wants to use, the devil is in the details—those deviations may be large, both absolute and percentage-wise, and worse, across all traits, a few traits may be wildly imbalanced and completely wreck things. And this is why investing in blocking/rerandomization (in experiments) or stratification/multi-level modeling (surveys) can give drastically improved results, by avoiding those imbalances.
This logic doesn’t apply solely to experiments or surveys—it applies to any kind of ‘sample’. Any sample may just be ‘weird’ on some single variable, not because there is anything interesting going on, but simply that each variable is a chance to be wildly imbalanced, and the more variables there are, the more lottery tickets one has purchased; as samples get smaller and variables get larger, the worse the problem gets. This is again a familiar observation about multiplicity and winner’s curses, but easy to forget.
One scenario is when we consider small groups of humans like colonizers. For example, the Amish in North America, who now number in the millions, were founded by an tiny group of founders, perhaps 500 in the main group, of whom many would not have reproduced further, because they arrived with their children as part of that 500 or didn’t reproduce or lineage wound up going extinct etc. (Let’s round that to an effective population of 100.) We are not surprised by founder effects on rare mutations: one father happens to carry a unique recessive gene which makes your spleen explode at age 30, and it is harmless until his collective offspring become so common that double-recessive children become possible and now medical geneticists get to study Swartzentruber’s Spleen Explosion Disorder etc. But we might say that, unless there were things specifically selected for by the Amish emigration process (as is quite likely given what an unpopular religion & extreme action that was, but needs to be proven case by case) we don’t expect any exotic effects on common genes or traits. With the sort of familiar normally distributed trait like height, we wouldn’t expect the Amish to be, say, a foot taller by mere chance throwing some taller Amish into the initial sample of 100 and this height deviation being inherited ever since, because the fluctuation on each variable is relatively small: a random sample of 100 on a 𝒩(0,1) variable has a standard error of 1/√100 = 0.1, so any noticeable height change like a few centimeters (|1SD|) would be highly unlikely—even |0.3SD| is rare at ~0.3%. So, if we were interested in height specifically, then a priori, we would not expect to find a large difference in height, either more or less; if we did find a −0.3SD difference, we should be skeptical of a founder effect on the trait and look to some other cause (nutrition? some rare variant? founders pre-selected to be shorter somehow? Amish women preferring shorter husbands?).
But that’s only one variable. What if we had instead noticed that Amish were weird on some variable, and went looking because of that? That’s not the same thing, because now we are implicitly looking at every possible variable that anyone could notice a deviation on; there are thousands upon thousands of human traits, and the odds of any one being weird is small, but the odds of none of them being weird are even smaller. If |0.3SD| on a single trait has only P = 0.3%, then the probability of thousands of independent traits all being <|0.3SD| must then be (1 − 0.3%)thousands = around zero. For example, for 10,000 traits describing the universe of normal human traits, we would expect to find with high probability 1 trait which is fully |0.4SD| (along with a bunch of |0.3|, |0.2|, |0.1| etc), mean of ~|0.38SD|. We could simulate this, or observe that this scenario is equivalent to asking what is the expected maximum of 10,000 samples which have an SD of the standard error from before, 0.1. (All normals have the same expected max, just rescaled by any difference in mean or variance.)
This would mystify any observer if it happened to a trait we observe routinely and are acutely sensitive to differences in, like height; why is X 0.4SD larger (or smaller) than everywhere else? What deep reason is there for it? (None, it was just a founder effect.) It would also be mystifying if it interacted with other things like tail effects in a liability-threshold model; if it hit something like schizophrenia, increasing genetic liability by 0.4SDs on average, the rate would double from 1% to ~2% (with population rate 1%, heritability 80%, +0.4SD genetic liability on average).
## expected max of 𝑘 normally distributed traits, given an initial sample of 𝑛 datapoints:
k <- 10000; n <- 100; exactMax(k) * (1 / sqrt(n))
# [1] 0.382963271
## Monte Carlo approximation thereof:
mean(replicate(1000, max(replicate(10000, abs(mean(rnorm(100)))))))
# [1] 0.400673883
## We could also have sampled from the extremes if we were curious about beyond the expectation:
## /order-statistic#sampling-sports-extremes-hypothetical-human-all-stars-league
# liability-threshold for a highly-heritable trait skewed up +0.4SD:
(1 - pnorm(qnorm(0.99) - ((0.8)^2 * 0.4))) / 0.01
# [1] 1.92098897Oh Deer: Could Deer Evolve to Avoid Car Accidents?
Can deer evolve under the selection pressure of car accidents to learn to avoid roads? Probably, but it’ll take a long time.
I’ve noticed while driving many deer corpses over the years. Cars seem like they could be a major source of deer mortality. If they are, deer might be evolving behavior to avoid cars. But deer/car accident rates appear stable or increasing (perhaps due to human population growth & construction). How fast would we expect to see any deer adaptation?
Looking at some of the mortality statistics, I model it as a liability threshold trait being selected on via truncation selection, and calculate some hypotheticals about whether and how fast they could adapt.
Teal deer: “of course, but it’d be slow.”
While driving to NYC recently I passed 3 roadkill deer, a few of many I have seen over the years, and a thought re-occurred to me: “if all these deer are being killed by cars, shouldn’t they be evolving to avoid cars?” I’ve seen many dead deer and narrowly avoided a few myself while driving, and deer/car mortality is, if anything, much higher in states like Pennsylvania.12
Accident rates would not necessarily show a steep decline thanks to past selection, because the ‘environment’ is not static here: as cars get faster, accidents become more crippling or lethal to deer; the American population has expanded several-fold both in population count, per-capita vehicle miles, suburban living, territory fragmentation, and the deer population too has expanded many-fold (from ~0.5m a century ago to <30m now). So if there was highly effective ongoing selection reducing deer accident risk, we would still observe large absolute and proportional increases in accidents/deaths.
But I am still curious as to what sort of selection we could expect, which is a hint as to long-term trends—the American population is now relatively stabilized in terms of growth and vehicle-miles, and deer appear to have also reached a population equilibrium, so a gradual long-term decline in accident rates might be possible to see in the future if there is substantial response to selection.
Deer accidents seem to be fairly fatal: wild animals are always on the edge, and small injuries can compound into death, so looking at mortality will if anything underestimate the strength of selection. And of course there will be no single Mendelian genes, but being a complex behavioral trait, it is almost surely a highly polygenic additive trait. So we can treat it as truncation selection on a binary trait (“killed by a car”) in the liability threshold model.
For truncation selection, the two key parameters are the heritability of a ‘trait’, and the fraction of the population expressing the ‘trait’.
The heritability can only be guessed at. Car accidents ought to be heritable to some degree, because everything is, and many behavioral traits like risk aversion or diurnality or reaction-time or startle reflex or wanderlust would affect being hit by a car (a deer can reduce risk by avoiding roads entirely, not traveling far, waiting to cross until very late at night when there is no traffic or during the day when they can be easily seen). Response to selection need not cause some hardwired behavioral change like aversion to travel: it might yield something like the Baldwin effect, where the response is for behavioral flexibility, and more fit deer are better able to learn how to navigate traffic gaps by watching other deer or imitating their mother. The “anthropocene” has led to many animals evolving or otherwise learning how to adapt, with urban environments no exception13, so why would deer be any exception?
We can gain some optimism by contrasting deer with a case where I would not expect much adaptation: feral dogs. I am told that in countries like India, they are common, and commonly roadkill. Feral dogs are descended almost entirely from domesticated dogs, so they start off in a terrible position compared to wild deer: inclined to human contact, not as disturbed by noise and fire, leaving selection much to do. But feral dogs are commensal, at best, with humans, and must spend much time around or near them, whereas deer need only pass through a road as briefly as possible; breeding a feral dog which is good at avoiding traffic while still being good at all the other things is much harder than avoiding traffic, period, and the net selection will be minimal. And there is constant interbreeding & replenishment—resetting any selection that did occur (while domesticated deer do not exist at all, aside from reindeer in the distant North).
Complicating things is the possibility that the heritability is high but actual responses to selection are lower than expected when estimated in an univariate single-trait fashion, because there might be a genetic correlation with another fitness-influencing trait, where better car avoidance means worse values of that other trait—perhaps it would be easy to avoid cars by avoiding roads or traveling far, but this has the drawback of preventing relocation to avoid starvation or hunters, in which case response to selection will be small or even opposite of expected (this is plausibly one of the main reasons why wild populations may not evolve as fast as predicted: “The Missing Response to Selection in the Wild”, et al 2018).
I can only guess at the heritability, as I doubt heritabilities have been calculated for much in deer, but I would predict it’s <50% simply because wild animals are under constant selection and car-based selection would’ve started almost a century ago. It might seem impossible to calculate heritability for wild animals of a ‘trait’ like being hit by a car, but I think it’s doable. Wild animals have no twin studies or family pedigrees, of course, and methods like common-garden rearing likewise seem questionable, but one use tracking devices to follow families of deer until they all die to construct a pedigree with outcome of death; more feasibly, one could collect DNA samples from dead car-accident deer and dead non-accident deer, and compute genomic similarity with a procedure like GCTA (for SNP heritability) or whole-genome sequencing data (upcoming methods for recovering full heritability). But this hasn’t been done as far as I know. Oh well. We can look at a range of heritabilities 0-50%.
The fraction of deer hit is a little easier. Wild deer live ~3-4y on average (eg. et al 2004 on Key deer implies ~3.7y), sexually maturing ~1.5y, and of the ~25m deer in the USA, around 1.5m are killed by cars annually ~2012 (according to The Atlantic with no citation) so perhaps ~5% annual mortality from cars ( et al 2008 estimates 2% in a sampled Virginia county, while 2012 suggests 1.2m deaths out of 25m deer); if deer live 4 years and have a 5% annual risk of being killed by a car, then their lifetime risk should be 1 − 0.954 = 18% or perhaps 8%, which sounds like a reasonable range—a substantial source of mortality but probably less than hunting or starvation or disease.
The effect of a generation of truncation selection on a binary trait following the liability-threshold model is more complicated but follows a similar spirit. R implementation of pg6 of “Chapter 14: Short-term Changes in the Mean: 2. Truncation and Threshold Selection”, Lynch & Walsh:
threshold_select <- function(fraction_0, heritability, verbose=FALSE) {
fraction_probit_0 = qnorm(fraction_0)
## threshold for not manifesting schizophrenia:
s_0 = dnorm(fraction_probit_0) / fraction_0
## new rate of trait after one selection where 100% of past-the-threshold never reproduce:
fraction_probit_1 = fraction_probit_0 + heritability * s_0
fraction_1 = pnorm(fraction_probit_1)
## how much did we reduce trait in percentage terms?
if (verbose) {
print(paste0("Start: population fraction: ", fraction_0, "; liability threshold: ", fraction_probit_0, "; Selection intensity: ", s_0))
print(paste0("End: liability threshold: ", fraction_probit_1, "; population fraction: ", fraction_1, "; Total population reduction: ",
fraction_0 - fraction_1, "; Percentage reduction: ", (1-((1-fraction_1) / (1-fraction_0)))*100)) }
return(c(fraction_probit_1, fraction_1, fraction_0 - fraction_1))
}
threshold_select(1-0.18, 0.50, verbose=TRUE)
# [1] "Start: population fraction: 0.82; liability threshold: 0.915365087842814; Selection intensity: 0.320000021339773"
# [1] "End: liability threshold: 1.0753650985127; population fraction: 0.858894349391959; Total population reduction: -0.0388943493919587; Percentage reduction: 21.6079718844215"
# [1] 1.07536509851 0.85889434939 -0.03889434939
threshold_select(1-0.08, 0.50, verbose=TRUE)
# [1] "Start: population fraction: 0.92; liability threshold: 1.40507156030963; Selection intensity: 0.161593724197447"
# [1] "End: liability threshold: 1.48586842240836; population fraction: 0.931343036233605; Total population reduction: -0.0113430362336053; Percentage reduction: 14.1787952920067"
# [1] 1.48586842241 0.93134303623 -0.01134303623We can look at a range of scenarios for population prevalences 8-18%, and heritabilities 5%-50%. Aside from the per-generation increase in car-avoiding deer/decrease in deer-car accidents, it might also be interesting to calculate a hypothetical like “how many generations/years would it take for natural selection, in a static environment, to reduce lifetime mortality to 1%?”
thresholdModeling <- function(fraction_0, heritability, targetPercentage) {
firstGeneration <- threshold_select(fraction_0, heritability)
## estimate how many generations of truncation selection until a target percentage is reached:
i <- 1; fraction_i <- firstGeneration[2]
while (fraction_i < targetPercentage) {
i <- i+1
nextGeneration <- threshold_select(fraction_i, heritability)
fraction_i <- nextGeneration[2]
}
return(c(firstGeneration, i)) }
thresholdModeling(1-0.20, 0.5, 1-0.01)
df <- expand.grid(Fraction=(1-seq(0.08, 0.18, by=0.02)), Heritability=seq(0.05, 0.50, by=0.05))
df <- cbind(df, round(digits=3, do.call(rbind, Map(thresholdModeling, df$Fraction, df$Heritability, 0.99))))
colnames(df)[3:6] <- c("Threshold.latent", "Fraction.new", "Fraction.reduction", "Generations.to.onepercent")
df$Years <- round(df$Generations.to.onepercent * 3.5)
dfFraction |
Heritability |
Latent threshold |
Fraction 2nd |
Fraction reduction |
Generations to 1% |
Years |
|---|---|---|---|---|---|---|
0.92 |
0.05 |
1.413 |
0.921 |
-0.001 |
300 |
1050 |
0.90 |
0.05 |
1.291 |
0.902 |
-0.002 |
314 |
1099 |
0.88 |
0.05 |
1.186 |
0.882 |
-0.002 |
324 |
1134 |
0.86 |
0.05 |
1.093 |
0.863 |
-0.003 |
332 |
1162 |
0.84 |
0.05 |
1.009 |
0.843 |
-0.003 |
338 |
1183 |
0.82 |
0.05 |
0.931 |
0.824 |
-0.004 |
343 |
1200 |
0.92 |
0.10 |
1.421 |
0.922 |
-0.002 |
150 |
525 |
0.90 |
0.10 |
1.301 |
0.903 |
-0.003 |
157 |
550 |
0.88 |
0.10 |
1.198 |
0.884 |
-0.004 |
162 |
567 |
0.86 |
0.10 |
1.106 |
0.866 |
-0.006 |
166 |
581 |
0.84 |
0.10 |
1.023 |
0.847 |
-0.007 |
169 |
592 |
0.82 |
0.10 |
0.947 |
0.828 |
-0.008 |
171 |
598 |
0.92 |
0.15 |
1.429 |
0.924 |
-0.004 |
100 |
350 |
0.90 |
0.15 |
1.311 |
0.905 |
-0.005 |
104 |
364 |
0.88 |
0.15 |
1.209 |
0.887 |
-0.007 |
108 |
378 |
0.86 |
0.15 |
1.119 |
0.868 |
-0.008 |
110 |
385 |
0.84 |
0.15 |
1.038 |
0.850 |
-0.010 |
112 |
392 |
0.82 |
0.15 |
0.963 |
0.832 |
-0.012 |
114 |
399 |
0.92 |
0.20 |
1.437 |
0.925 |
-0.005 |
75 |
262 |
0.90 |
0.20 |
1.321 |
0.907 |
-0.007 |
78 |
273 |
0.88 |
0.20 |
1.220 |
0.889 |
-0.009 |
81 |
284 |
0.86 |
0.20 |
1.132 |
0.871 |
-0.011 |
82 |
287 |
0.84 |
0.20 |
1.052 |
0.854 |
-0.014 |
84 |
294 |
0.82 |
0.20 |
0.979 |
0.836 |
-0.016 |
85 |
298 |
0.92 |
0.25 |
1.445 |
0.926 |
-0.006 |
60 |
210 |
0.90 |
0.25 |
1.330 |
0.908 |
-0.008 |
62 |
217 |
0.88 |
0.25 |
1.232 |
0.891 |
-0.011 |
64 |
224 |
0.86 |
0.25 |
1.145 |
0.874 |
-0.014 |
66 |
231 |
0.84 |
0.25 |
1.067 |
0.857 |
-0.017 |
67 |
234 |
0.82 |
0.25 |
0.995 |
0.840 |
-0.020 |
68 |
238 |
0.92 |
0.30 |
1.454 |
0.927 |
-0.007 |
50 |
175 |
0.90 |
0.30 |
1.340 |
0.910 |
-0.010 |
52 |
182 |
0.88 |
0.30 |
1.243 |
0.893 |
-0.013 |
54 |
189 |
0.86 |
0.30 |
1.158 |
0.877 |
-0.017 |
55 |
192 |
0.84 |
0.30 |
1.081 |
0.860 |
-0.020 |
56 |
196 |
0.82 |
0.30 |
1.011 |
0.844 |
-0.024 |
57 |
200 |
0.92 |
0.35 |
1.462 |
0.928 |
-0.008 |
43 |
150 |
0.90 |
0.35 |
1.350 |
0.911 |
-0.011 |
44 |
154 |
0.88 |
0.35 |
1.255 |
0.895 |
-0.015 |
46 |
161 |
0.86 |
0.35 |
1.171 |
0.879 |
-0.019 |
47 |
164 |
0.84 |
0.35 |
1.096 |
0.863 |
-0.023 |
48 |
168 |
0.82 |
0.35 |
1.027 |
0.848 |
-0.028 |
48 |
168 |
0.92 |
0.40 |
1.470 |
0.929 |
-0.009 |
37 |
130 |
0.90 |
0.40 |
1.360 |
0.913 |
-0.013 |
39 |
136 |
0.88 |
0.40 |
1.266 |
0.897 |
-0.017 |
40 |
140 |
0.86 |
0.40 |
1.184 |
0.882 |
-0.022 |
41 |
144 |
0.84 |
0.40 |
1.110 |
0.867 |
-0.027 |
42 |
147 |
0.82 |
0.40 |
1.043 |
0.852 |
-0.032 |
42 |
147 |
0.92 |
0.45 |
1.478 |
0.930 |
-0.010 |
33 |
116 |
0.90 |
0.45 |
1.369 |
0.915 |
-0.015 |
34 |
119 |
0.88 |
0.45 |
1.277 |
0.899 |
-0.019 |
35 |
122 |
0.86 |
0.45 |
1.197 |
0.884 |
-0.024 |
36 |
126 |
0.84 |
0.45 |
1.125 |
0.870 |
-0.030 |
37 |
130 |
0.82 |
0.45 |
1.059 |
0.855 |
-0.035 |
37 |
130 |
0.92 |
0.50 |
1.486 |
0.931 |
-0.011 |
30 |
105 |
0.90 |
0.50 |
1.379 |
0.916 |
-0.016 |
31 |
108 |
0.88 |
0.50 |
1.289 |
0.901 |
-0.021 |
32 |
112 |
0.86 |
0.50 |
1.210 |
0.887 |
-0.027 |
33 |
116 |
0.84 |
0.50 |
1.139 |
0.873 |
-0.033 |
33 |
116 |
0.82 |
0.50 |
1.075 |
0.859 |
-0.039 |
34 |
119 |
As expected, scenarios where deer accidents are rare achieve 1% faster (less work to do), and higher heritabilities produce faster responses (more useful genes). In most of the scenarios, the annual percent reduction is small, no often less than a percentage point, so would be easy to miss, and the almost complete elimination of deer-car accidents would take centuries of adaptation even with a fixed environment.
So while deer might be evolving to reduce accident mortality, it would be hard to see and won’t help much anytime soon. (For the same reasons, I would expect squirrel-based power outages to continue indefinitely.) So if it’s a problem, one’d better hurry up with safety measures like road fencing or self-driving cars.
Evolution As Backstop for Reinforcement Learning
Acne: a Good Quantified Self Topic
Fermi Calculations
Selective Emigration and Personality Trait Change
2019 finds that the emigration of 25% of the Scandinavian population to the USA 1850–701920105ya was driven in part by more ‘individualistic’ personality factors among emigrants, leading to permanent decreases in mean ‘individualism’ in the home countries. This is attributed to cultural factors, rather than genetics. I model the overall migration as a simple truncation selection scenario, and find that in a simple model under reasonable assumptions, the entire effect could be genetic.
In “Those Who Stayed: Individualism, Self-Selection and Cultural Change during the Age of Mass Migration”, 2019, Knudsen examines one of the largest emigrations from Europe to the USA, from Scandinavian countries like Sweden: over about two generations, 25% of the entire population left for the USA. (The effects of this emigration will be familiar to anyone who has visited the Midwest.) Who left is not random at all, and would be influenced by personality traits; Knudsen uses noisy proxies to measure personality traits like ‘individualism’ on a population level, and finds that because of the emigration of Scandinavian individuals high on these traits, the remaining population is noticeably lower on them, by “approximately 3.9%-points in Denmark, 10.1%-points in Sweden, and 13.1%-points in Norway”, and more interestingly, these reductions appear to be permanent:
Several circumstances make the Age of Mass Migration an ideal case for the empirical objective of this paper. During the period, millions of people left Europe to settle in New World countries such as the United States. Sweden, Norway, and Denmark experienced some of the highest emigration rates in Europe during this period, involving the departure of approximately 25% of their populations. Besides representing the largest migration event in Scandinavian history, global regulatory policies on migration were particularly loose at this point in time, which enables the identification of self-selective processes under limited governmental influence. In addition, the historical context allows me to study long-run cultural implications of migration in sending locations.
For use in analyses of aggregate district effects, I quantify the cultural shock of selective emigration as the percentage point drop in the prevalence of individualists in the migrant-sending population that occurs due to emigration. This is feasible because I have information on rates of emigration and the gap between emigrant and population individualism. Accumulating these shocks over the entire period of the Age of Mass Migration reveals an overall reduction in individualism from emigration of approximately 3.9%-points in Denmark, 10.1%-points in Sweden, and 13.1%-points in Norway…Fixed-effects estimations document that the cultural shocks of emigration pushed migrant-sending district culture in a collectivist direction and this is robust to the inclusion of control variables that capture alternative district, cohort, and emigrant characteristics
The shock measures are available from 1860165ya onwards, since these are the decades covered by the emigrant passenger lists. The cultural shocks of emigration can be calculated for any time period and aggregation level. I produce baseline measures at the district and decade level. The accumulated shock over the entire Age of Mass Migration equals a loss of individualists of 3.9%-points in Denmark, 10.1%-points in Sweden, and 13.1%-points in Norway. Although the measure most precisely reflects shocks to the distribution of inherited individualism in the home population, they also approximate shocks to the distribution of actual individualism if emigrants and non-emigrants are assumed to abandon their cultural heritage at similar rates. The rate and cultural shock of emigration correlate strongly around a ratio of 0.4 (see scatter plot and histogram in Appendix Figures A.1 and A.3).23
(2019 also show emigration effects in Sweden related to communalism, leading to greater voting/labor union/strike participation.)
Why are they permanent? Knudsen only mentions ‘cultural transmission’, but of course, they have to also be partially genetic: personality traits are heritable, and so selecting on personality will cause genetic changes, and we can see population stratification caused by selection on complex traits (like intelligence/education in the UK: “Genetic Consequences of Social Stratification in Great Britain”, et al 2018). A process like emigration has no way of somehow letting only people emigrate who are ‘individualistic’ for purely environmental reasons, after all; such processes see only phenotypes, which are the outcome of both genes and environments.
Is it plausible that genetics might explain a nontrivial amount of the reduction? The selection effect here is relatively small: only 25% of the total population left, once, and while ‘individualism’ might be a big part of decisions to live, there are surely many other genetic and environmental factors and sheer randomness in any individual’s decision to leave. It feels like the genetic effect might be much too small to be particularly relevant.
We can quickly estimate expected effects by treating this as truncation selection in a liability threshold model (“Chapter 14: Short-term Changes in the Mean: 2. Truncation and Threshold Selection”, Lynch & Walsh): the bottom X% are ‘truncated’ from the population (because they physically left for the USA and did not return, a binary variable) in a single selective step, and we want to know the effect on personality traits of a certain heritability (which can be extrapolated from research on more-carefully measured personality traits like the Big Five) given that they are r < 1 with the emigration variable (we can only guess at the values here—surely r < 0.5?).
Knudsen says the overall selection is 25%; this would be over perhaps 2 generations, but since it’s such a short period and small effects, it doesn’t make much of a difference if we treat it as a single big population.
What is the overall effect on personality? Knudsen includes some graphs showing emigration rates by country over time, but I don’t see any population-weighted average overall effect reported in her paper. (Bringing up the question of how much of the effect is genetic with Knudsen on Twitter, she mentioned that she was working on revisions which would include more information on effect sizes and what other individual differences might cause the emigration decision.) The observed effect is 3.9%/10.1%/13.1% (Norway/Sweden/Denmark), which averages to 8%:
library(psych); geometric.mean(c(3.9, 10.1, 13.1))
# [1] 8.02082595Sweden is presumably by far the biggest country of the 3 at the time and would influence the average the most, so 8% is probably too small, but serves as a benchmark. It would be more convenient to have this in standard deviations but I don’t see anywhere Knudsen gives it in SDs rather than percentages. I think what is done there is treat the population as a standardized variable and then the conversion was to convert percentiles to SDs; then that suggests an “8% decrease” would be equivalent to a 0.19SD change:
qnorm(0.99) / 99
# [1] 0.0234984634
(qnorm(0.99) / 99) * 8.02
# [1] 0.1884576760.19SD isn’t so big, and looks somewhat plausible. Perhaps truncation selection can explain this change after all.
To estimate the change, we convert the percentage to an SD threshold: how low a score does it take to be in the bottom 25%14 and thus emigrate?
qnorm(0.25)
# [1] -0.67448975So we can imagine everyone with a ‘communalism’ score of <-0.67 emigrated. In a population of 𝒩(0,1), if we delete everything <-0.67, giving a truncated normal distribution what does the remainder average?
truncNormMean <- function(a, mu=0, sigma=1, b=Inf) {
phi <- dnorm
erf <- function(x) 2 * pnorm(x * sqrt(2)) - 1
Phi <- function(x) { 0.5 * (1 + erf(x/sqrt(2))) }
Z <- function(beta, alpha) { Phi(beta) - Phi(alpha) }
alpha = (a-mu)/sigma; beta = (b-mu)/sigma
return( (phi(alpha) - phi(beta)) / Z(beta, alpha) ) }
truncNormMean(qnorm(0.25))
# [1] 0.423702097So the survivors, as it were, have shifted from an average of 0SD to +0.42SD on ‘communalism’ (anti-‘individualism’).
This, however, is not the genetic increase. It includes all the variables, not just genes, like rearing or random noise, which affect personality, and then all of the variables which affect emigration risk above and beyond personality. So it must be decreased twice to compensate for personality being only partly genetic, and then emigration being only partly personality (ie. genes → personality → emigration has 2 arrows which are r < 1).
Personality factors like the Big Five personality traits well-established as having heritabilities ~50% (eg. Bouchard & 2003), so would correlate √0.50 = 0.71. ‘Individualism’/‘communalism’ is of course not exactly the Big Five, and in Knudsen correlates with many other traits associated with social & economic success, and so it may reflect much more than something like Openness; intelligence is probably part of it, and intelligence has a substantially higher heritability than the Big Five, so I might be underestimating ‘individualism’ here.
How much of emigration is personality? I can’t give an exact value here: Knudsen’s analysis probably implies a value somewhere, but she is using imperfect proxies with a lot of measurement error, so I wouldn’t be sure how to interpret them anyway. I’d be surprised if it was r > 0.5, simply because few variables exceed that in psychology or sociology, and one would expect emigration to be influenced by proximity to ports, local economic & weather conditions, chain migration, individual & familial wealth, etc—so consider an example with r = 0.5 as a best-case scenario.
We deflate the truncated normal mean by the 2 variables:
truncNormMean(qnorm(0.25)) * sqrt(0.5) * 0.5
# [1] 0.149801313
(truncNormMean(qnorm(0.25)) * sqrt(0.5) * 0.5) / (qnorm(0.99) / 99)
# [1] 6.3749408So in this truncation selection scenario, we’d predict a +0.15SD or ~6% increase. This is not too far off the Knudsen estimates of 0.19SD or 8%, and quite small changes could equalize them (eg. r = 0.62 for personality → emigration would be enough).
So it seems that the truncation selection is stringent enough, and the observed effects small enough, that genetics could indeed explain most or all of it.
See Also
The Most Abandoned Books on GoodReads
Best Student Ever!
Little’s Law in the Wild
Tail Collapse
Richard Hamming, “You and Your Research”:
↩︎The three outstanding problems in physics, in a certain sense, were never worked on while I was at Bell Labs. By important I mean guaranteed a Nobel Prize and any sum of money you want to mention. We didn’t work on (1) time travel, (2) teleportation, and (3) antigravity. They are not important problems because we do not have an attack. It’s not the consequence that makes a problem important, it is that you have a reasonable attack. That is what makes a problem important.
-
↩︎The consensus among NICE’s economic advisers is that NICE should, generally, accept as cost effective those interventions with an incremental cost-effectiveness ratio of less than £20,000 per QALY and that there should be increasingly strong reasons for accepting as cost effective interventions with an incremental cost-effectiveness ratio of over £30,000 per QALY.
This renders the population estimate a bit off, but I couldn’t find any sources on the breakdown of Sephardic vs Ashkenazi in the USA in 197055ya other than a comment that the latter were a “vast majority”. Since the Jewish Population Study was probably an undercount in not including all the people of Jewish descent, I’m hopeful those two biases cancel out.↩︎
The high IQ sample in 1964 would have been >8% Jewish, but the paper only reports the overall Jewishness, without specifying whether it’s 4% vs 12% or something like that.↩︎
1937: “The data of the present study were obtained early in 193392ya, the subjects being 36 boys and 19 girls, of the average age of 18 years 6 months. The IQ’s (S-B) of all had been taken in early childhood (9). The group ranged from 135–190 IQ (S-B), with a median at about 153 IQ (S-B). All but 4 of these young persons were Jewish, a factor which must be considered as of possible consequence8, 14…”↩︎
et al 1993, pg3–4:
↩︎The mean IQ of the Hunter sample was 157, or approximately 3.5 standard deviations above the mean, with a range of 122 to 196 on the L-M form. [Stanford-Binet Intelligence Scale, Form L-M (SBL-M)]
…Each class at Hunter College Elementary School from the years 194877ya to 196065ya contained about 50 students, yielding a total possible population of 600 graduates…35% of the total population of 1948–12196065ya HCES students (n = 210) completed and returned study questionnaires
…Religious Affiliation: The Hunter group is approximately 62% Jewish, although they describe themselves as Jews more in terms of ethnic identity than religious practice. The group, as a whole, is not religious.
Educational Attainments: Over 80% of the study participants held at least a Master’s degree. Furthermore, 40% of the women and 68% of the men held either a Ph.D, LL.B., J.D., or M.D. degree. Occupation and Income: Only two of the HCES women identified themselves primarily as homemakers. 53% were professionals, working as a teacher at the college or pre-college level, writer (journalist, author, editor), or psychologist. The same proportion of HCES men were professionals, serving as lawyers, medical doctors, or college teachers. The median income for men in 1988 was $75,000 (range = $500,000) and for women $40,000 (range = $169,000). Income levels were substantially different for men and women, even when matched by profession. For example, the median income for male college teachers or psychologists was $50,000 and for females, $30,000.
In retrospect, I could have sped this up considerably by using the beta transform trick of order statistics to sample the tail directly rather than generating the entire sample.↩︎
My first attempt at it in JAGS went like this:
model_string <- ' model { cutoffIQ <- 100 + 3.719016485*15 mu_asian ~ dnorm(105, 4^-2) X_asian ~ dnorm(mu_asian, 15^-2) # T(cutoffIQ,) X_frac_asian <- X_asian > cutoffIQ P_asian <- 0.07 * (X_frac_asian / length(X_asian)) Y_asian ~ dbinom(P_asian, total) # mu_white ~ dnorm(100, 4^-2) # X_white ~ dnorm(mu_white, 15^-2) # T(cutoffIQ,) # X_frac_white <- X_white > cutoffIQ # P_white <- (1-0.07) * (X_frac_white / length(X_white)) # Y_white ~ dbinom(P_white, total) } ' library(runjags) Y_asian=126 Y_white=418 total=579 model <- run.jags(model_string, data = list(Y_asian=Y_asian, Y_white=Y_white, total=total), monitor=c("mu_asian", "mu_white"), n.chains = getOption("mc.cores"), method="rjparallel") summary(model)But then I realized that
X_frac_asian <- X_asian > cutoffIQdidn’t do what I thought it did and I needed to somehow draw a large number of samples, just like in the ABC simulation, and compare to the number after the truncation… or something.↩︎Strictly speaking we could probably do a parametric bootstrap by counting per decade, and treating each one as a Poisson estimation, and generating random deviates, but that runs into issues with decades with 0 figures (the MLE might estimate a rate of 0 which we know is wrong but not what rate might be right, which could easily imply average rates >1 based on surrounding temporal trends).↩︎
I’ve been experimenting with Boomerang to reduce the problem of non-followups by setting ‘ping me if no reply within 1 month’ alerts on my sent emails.↩︎
In this context, it’s interesting to note Cavalli-Sforza’s role in Lewontin’s fallacy.↩︎
Why do deer, and squirrels especially, keep getting run over, even as plenty of other animals like cats or foxes manage to avoid it? (On one walk, I noted 2 dead squirrels in a 10-meter stretch of road that regularly kill squirrels; on finishing my walk, there were 3. Meanwhile, the neighborhood cats will calmly sit a few feet from the road and watch you roar by.) My best guess is that it’s a maladaptive predator-avoidance strategy: a chasing predator will head straight for the prey as the fastest route, so prey will wait to the last second to dodge left or right at random as a Nash equilibrium. Unfortunately, a car is not a predator and is generally not heading straight at them, so that strategy means half the time they maximize their danger of being run over. Conversely, predators do not seem to have this strategy hardwired: I am reminded of a time I went walking in heavy fog, when I saw the glow of oncoming headlights from a pickup truck, and was shocked to see, running straight at me down the shoulder, a terrified kitten. It had only to jump right a foot into some friendly bushes, or 5 feet left, but it was so panicked all it could think to do was to run straight away, nearly guaranteeing that it would be run over. I had stepped off the road to avoid the truck, but, perhaps thinking I could grab it, I stepped into its path, and it panicked into the bushes—which did solve the problem.↩︎
Some relevant links:
“Global urban signatures of phenotypic change in animal and plant populations”, et al 2017
“Signatures of positive selection and local adaptation to urbanization in white-footed mice (Peromyscus leucopus)”, Harris & Munshi-2017 (city mice adapting to eat human food)
Moscow subway dogs (not necessarily genetic except perhaps in a Baldwin effect way, but a demonstration of behavioral flexibility/learning)
Ridley: “Cities Are the New Galapagos”/“The Sixth Genesis: a man-made, mass-speciation event”
Darwin Comes to Town: How the Urban Jungle Drives Evolution, 2018
I find it a bit easier to avoid phrasing it as “decreasing individualism” and think of the opposite way as “increasing communalism”, because most discussions of threshold selection are—unsurprisingly given the major use is in breeding—framed as about increasing levels of some trait.↩︎