The Ups and Downs of the Hope Function In a Fruitless Search
On Bayesian updating of beliefs in sequentially searching a set of possibilities where failure is possible, such as waiting for a bus; the psychologically counterintuitive implication is that success on the next search increases even as the total probability of success decreases.
This transcript has been prepared from a scan of chapter 15, pages 353–377 in Subjective Probability 199432ya, edited by G. Wright & P. Ayton. All links are my own insertion; references have been inserted as footnotes at the first citation.
**
to hide apparatus like the links, you can use reader-mode ().
15. The Ups and Downs of the Hope Function In a Fruitless Search
by Ruma Falk (The Hebrew University, Jerusalem), Abigail Lipson (Harvard University), and Clifford Konold (University of Massachusetts, Amherst)
It is seldom, if ever, that human beings are not actively searching for something. They may be searching for the next correct turning in the road they travel; for a misplaced object of value; for a name to put to the familiar face that suddenly confronts them; or for a solution of tomorrow’s problems. All such search is beset with uncertainties.
(Bell, 197947ya, page 141)
Imagine searching for a paragraph that you read some time ago. You have a visual memory of that paragraph on a right-hand page of a book, toward the top. Though you think you remember the particular book, you are not absolutely certain. Systematically, you begin leafing through the book’s 10 chapters. The paragraph does not turn up in the first chapter, or in the second, third… As you proceed without success through the chapters, does your hope of finding the paragraph in the next chapter increase or decrease?
[pg354]
And what of your hope of finding it in the book at all? Imagining yourself in this familiar situation, you may feel that before you reached the end of the book, despair would set in (“this must be the wrong book”). On the other hand, the longer you search the more reluctant you may be to quit, not only because of the efforts invested up to now, but because of a persisting intuition that the changes of finding the paragraph in the next chapter increase after each successive disappointment.
We all too often find ourselves in this type of search process. Without a realistic assessment of the uncertainties involved, we may either overestimate our chance of success, thus wasting more time in a futile search, or underestimate our chances, giving up too early in frustration and unjustified despair (MacGregor, Fischhoff, & Blackshaw, 1987). Considering the simplicity of the search situation in question and everybody’s familiarity with the experience, it has surprised us to find that studies analyzing probabilistic reasoning in such situations are scarce. The psychological studies concerning search that we found deal mostly with seeking strategies, not with the course of the searcher’s optimism throughout a systematic search characterized by prior uncertainty. (We make this statement despite realizing that our own search strategies might have been suboptimal; we might have abandoned the search prematurely.)
Bell (197947ya) reviews investigations of several types of physical search, conducted mainly by John Cohen and his collaborators. In their studies, subjects (children) choose locations in which to search for an object which is known for sure to be in one of the available locations (see, eg. Cohen & Meudell, 1968, Experiment 4). Thus, subjects’ hope assessments (confidence ratings) in these studies confound probabilistic judgments with evaluations of the wisdom of their own choices. Another class of studies concerns search decisions and confidence assessments in complex hierarchical systems. These studies include investigations of locating general items of knowledge in a Statistical Abstract, and searching computerized databases (see, for example, MacGregor, Fischhoff & Blackshaw, 198739ya, and references therein).
The more typical real-world search process involves situations where initial uncertainty about the existence of a target object in a finite field of locations is followed by a systematic search of these locations, with a series of negative results. We have encountered variations of such situations in math-education journals, in popular scientific literature, in fiction, and in daily living. Consider the following 4 examples.
Example 1 The Case of Sherlock Holmes.
In Arthur Conan Doyle’s story, “The 6 Napoleons” (cited by Jones, 19662), the great detective Sherlock Holmes deduces that one of 6 plaster busts of Napoleon conceals a priceless pearl. As the story unfolds, the busts are smashed one by one, until Sherlock finds and dramatically smashes the last one, recovering the pearl. As usual, the detective reveals his reasoning, noting that the numerical chances of finding [pg355] the pearl in the next bust increased as their number dwindled, until with the last bust it reached certainty. Jones (196660ya) points out that the scientific viewpoint would doubt Sherlock’s initial certainty, and would start with, say, only a 50% chance that Sherlock’s theory is right: “As successive busts are smashed and no pearl is found, the rising chance of finding it in the next is balanced by the evidence of this growing succession of failures that Sherlock is wrong, and that there isn’t any pearl at all.” (page 466)
Example 2 Doctor Fischer’s Bomb Party
Graham Greene’s (198046ya) Dr Fischer wants to test the limits of greediness. He invites 6 wealthy guests to a party and shows them a barrel in a corner of his garden in which are 6 Christmas crackers. 5 of the crackers, he explains, contain a cheque for 2 million Swiss Francs. The 6th contains enough explosive so primed as to end the life of whoever pulls the cracker. The guests are challenged to approach the barrel one by one and try their luck. Dr Fischer assures them that the cheques are there, but the matter is complicated by the possibility that the presence of the bomb might be a hoax. While one of the guests prepares (hesitantly) to make his move, he is preempted by Mrs Montgomery who pushes ahead of him to the barrel, explaining that “the odds would never be as favorable again” (Greene, 198046ya, page 127). Is she right? (See Ayton & McClelland’s, 1987, delightful paper on that ghastly party.)
Example 3 The Key Problem.
A man comes home at night during a blackout. He has 2 similar bunches of keys in his pocket; one for home, one for work. In the darkness, he picks one bunch from his pocket. The bunch comprises n keys of which only one will fit his door; if, that is, he has picked the right bunch. He tries the keys successively (sampling without replacement). We are interested in his confidence that he’s got the right bunch, and in his immediate expectancy of unlocking the door when key after key fails to do the job (L.V. Glickman, personal communication, 198442ya. Adapted from a problem in Feller, 19573, page 54.)
Example 4 Let Sleeping Flies Lie.
Raphael Falk, a Hebrew University geneticist, told us about his experience of expecting a phone call from the Dean of his faculty. The Dean had told him the previous day that he might call him in his lab between 10 and 11 a.m. Raphael spent that morning examining successive bottles inhabited by Drosophila flies, looking for a certain rare mutant. His routine was to etherize the flies in each bottle for a few minutes and then inspect them under the microscope. If the inspection were to be interrupted, the flies would wake up and fly away. He kept working calmly until about 10:30 a.m., by which time the Dean had still not called. Raphael reported feeling that the chances of the Dean calling were dropping steadily as time went on. However, he became increasingly nervous about etherizing [pg356] the flies in each successive bottle, fearing that the Dean’s impending call would disrupt the inspection.
In order to investigate the nature of probabilistic reasoning in situations like those described above, we devised 2 experimental problems, each of which involved 2 hope questions (long-term and short-term). Problem 1 (inspired by Meshalkin, 196363ya/19734, page 21) concerns a standard search situation (similar to Example 3). Problem 2 involves an equivalent wait situation (similar to Example 4). The 2 situations are structurally analogous, although the first describes an active search process while the second describes an extended wait for a target event to occur.
We will present the 2 standard problems along with the Bayesian solution. Then we will discuss a number of features of the solution by applying it to a variety of situations including the 4 examples just cited. After describing how our subjects reasoned about the standard problems, we will present a didactic device we developed to make the search problem more conducive to resolution. Finally, we will explore subjects’ ability to transfer the lesson learned from the didactic device to the analogous wait problem.
15.1 Standard Problems and Their Solution
Problem 1 The Standard Search Problem. The Desk: Seek and you Shall Find?
Long-term probability version (Desk-long—DL). Imagine that you are searching for an important letter that you received some time ago. Usually your assistant puts your letters in the drawers of your desk after you have read them. He remembers to do this in 80% of the cases, and in 20% of the cases he leaves them somewhere else.
There are 8 drawers in your desk. If indeed your assistant has placed the letter in your desk, you know from past experience that it is equally likely to be in any of the 8 drawers.
You start a thorough and systematic search of your desk.
You search the first drawer, and the letter is not there.
How would you now evaluate the probability that the letter is in the desk?
You continue to search the next 3 drawers, until altogether you have searched 4 drawers. The letter is not there.
How would you now evaluate the probability that the letter is in the desk?
You continue to search 3 more drawers, until altogether you have searched 7 drawers. The letter is not there. [pg357]
How would you now evaluate the probability that the letter is in the desk?
Short-term probability version (Desk-Short—DS). Same problem-stem as DL, but the 3 questions are:
You search the first drawer, and the letter is not there.
How would you now evaluate the probability that the letter is in the next drawer (ie. in the second drawer)?
You continue to search the next 3 drawers, until altogether you have searched 4 drawers. The letter is not there.
How would you now evaluate the probability that the letter is in the next drawer (ie. in the fifth drawer)?
You continue to search 3 more drawers, until altogether you have searched 7 drawers. The letter is not there.
How would you now evaluate the probability that the letter is in the next drawer (ie. in the 8th drawer)?
Problem 2 The Standard Wait Problem. At the Bus Stop.
Long-term probability version (Bus-Long—BL). Imagine that you and your friend are tourists in a big foreign city. You find yourself late in the evening looking for transportation back to your hotel. You approach a bus stop that doesn’t display any timetable. You know, however, that the buses in this city run punctually each half hour during the evening, only it is now so late that you are somewhat worried that they might have already stopped running.
You do know that 60% of the bus routes in the city operate this late, and 40% do not, but you don’t know whether this particular bus is still running or not. It is now 11:30 p.m., and you decide to wait until either the bus arrives or midnight, whichever happens first.
Since you have no idea about the bus’s exact schedule, you figure that the bus is equally likely to arrive in any of the 6 5-minute intervals during the coming half-hour (if indeed it is still running).
The bus does not arrive in the first 5 minutes. It is now 11:35.
How would you now evaluate the probability that the bus will arrive sometime before midnight?
Another 10 minutes elapse. The time is now 11:45, and the bus has not arrived.
How would you now evaluate the probability that the bus will arrive sometime before midnight?
10 more minutes go by. The time is now 11:55, and the bus has not arrived.
How would you now evaluate the probability that the bus will arrive sometime before midnight?
[pg358]
Short-term probability version (Bus-Short—BS). Same problem-stem as BL, but the 3 questions are:
The bus does not arrive in the first 5 minutes. It is now 11:35.
How would you now evaluate the possibility that the bus will arrive during the next 5 minutes (ie. between 11:35 and 11:40)?
Another 10 minutes elapse. The time is now 11:45, and the bus has not arrived.
How would you now evaluate the probability that the bus will arrive during the next 5 minutes (ie. between 11:45 and 11:50)?
10 more minutes go by. The time is now 11:55, and the bus has not arrived.
How would you now evaluate the probability that the bus will arrive during the next 5 minutes (ie. between 11:55 and midnight)?
15.1.1 The Mathematical Long-Run and Short-Run Functions
We solve the Standard Search Problem (Problem 1) for the general case of n equally likely drawers and prior probability L0 that the letter is in the desk. The solution applies as well to the isomorphic Wait Problem (Problem 2). If the letter is in the desk, the conditional probability of not finding it when searching the first i drawers is ; if the letter is out of the desk, not finding it in the first i drawers is a certainty. Let’s denote the respective long-term and short-term posterior probabilities we wish to find by Li = P (letter is in desk | letter was not in first i drawers), Si = P (letter is in next drawer | letter was not in first i drawers). Clearly, S0 = L0⧸n, and . By Bayes’ rule:
A few algebraic manipulations yield:
(15.1)
(15.2)
Formulas (15.1) and (15.2) describe the hope functions for the long run (Li) and the short run (Si), given i initial failures.
Table 15.1 presents the specific forms which Li and Si assume in the case of Problems 1 and 2, along with the answers to the questions posed in the Problems. The numbers in Table 15.1, as well as formulas (15.1) and (15.2), indicate the long-term hope function, Li, decreases as i grows, whereas the short-term hope function, Si, increases with i, until Ln−1 = Sn−1.
[pg359]

long-term and short-term hope functions for the desk and bus problems (Problems 1 & 2)
15.1.2 Further Explorations
A number of issues surface as we extend our formal analysis to the examples cited earlier. Suppose L0 = 1, as in the case of Sherlock’s absolute confidence that the pearl is hidden in one of the busts (Example 1). If indeed there is no doubt whatsoever about the existence of the target object in one of the available locations, no initial sequence of failures, long as it may be, will shatter that (long-term) certainty. Li will equal 1 for all values of i. The short-term probability of success in the next unit (location or time slot) will equal the inverse of the number of remaining units and will thus rise to 1 when only one unit remains (ie. for i = n−1). The results for the case of initial certainty may also be obtained from formulas (15.1) and (15.2) by substituting 1 for L0. These formulas are, in fact, valid for the entire range of possible values of L0, including the end points 1 and 0.
Figure 15.1
Figure 15.1 presents the long-term and the short-term hope functions for the data of the standard search problem (Problem 1). Sherlock’s short-term hope function (Example 1), in which L0 = 1 and n = 8, is added for comparison (inspired by Jones, 196660ya).
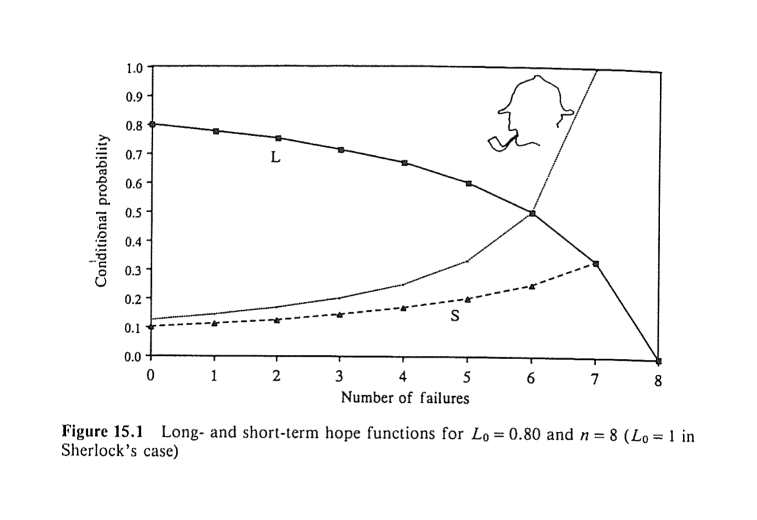
long-term and short-term hope functions for L0 = 0.80 and n = 8 (L0 = 1 in Sherlock’s case)
Dr Fischer’s bomb party (Example 2) raises a third question, in addition to our long-term and short-run questions: Which (if any) is the safest serial position beforehand? The a priori probability of blowing the bomb (finding the object) in ordinal position (location) i, denoted Ai, can be successively computed [pg360] given L0. Suppose L0 = 1⁄2. Let n be 6, as in Greene’s (198046ya) story. The conditional probability Li that a bomb exists in the barrel, given that i crackers have been safely pulled, is obtained by applying (15.1) to the present case:
For player i, we multiply the probability of the previous i-1 players not detonating the bomb by the conditional probability of the presence of a bomb given that information (ie. Li−1). We then multiply that result by the probability of player i pulling the bomb-cracker out of the remaining 6-i+1 crackers. These 3 factors are listed, in turn, in each row of Table 15.2. Computing these products, we see that the a priori probabilities of pulling the bomb are the same for all the ordinal positions (Ayton & McClelland, 198739ya). The function Ai is thus constant over all the values of i. There was no reason for Mrs Montgomery to rush to play first.
In hindsight, it should have been obvious that, prior to starting the game, all the participants are equally likely to detonate the bomb (just as the a priori probabilities of finding the letter in any of the drawers of the desk are equal). Without loss of generality, we can imagine that instead of going in turn, the 6 players are assigned a cracker at random, and they all pull simultaneously. The modified version is evidently symmetric with respect to all players. Consequently, their chances of detonating the bomb are equal (see Falk, 19935, Problems 2.3.3, 2.4.12, and 2.4.13).
[pg361]
Table 15.2
A priori probabilities of blowing the bomb as a function of serial position. L0 = 0.50; n = 6 (Example 2)
i |
Ai |
|---|---|
1 |
1 × 1⁄2 × 1⁄6 = 1⁄12 |
2 |
11⁄12 × 5⁄11 × 1⁄5 = 1⁄12 |
3 |
10⁄12 × 4⁄10 × 1⁄4 = 1⁄12 |
4 |
9⁄12 × 3⁄9 × 1⁄3 = 1⁄12 |
5 |
8⁄12 × 2⁄8 × 1⁄2 = 1⁄12 |
6 |
7⁄12 × 1⁄7 × 1 = 1⁄12 |
As we saw, our hope functions, which are defined as conditional probabilities given an initial sequence of i negative outcomes, are generally not constant (see Figure 15.1). This is true for all cases, barring Li when L0 = 1 (Example 1). In terms of Dr Fischer’s bomb party (Example 2), the course of the function L implies that “if we entertain any degree of doubt concerning the presence of a bomb in any of the crackers then that doubt will be fueled the more crackers that are pulled without a bomb exploding” (Ayton & McClelland, 198739ya, page 180). At the same time, the course of the function δ indicates that the risk of the next cracker blowing up increases with the number of innocuous crackers that have been pulled.
By the same token, the man who tries consecutive keys in the bunch and fails to unlock the door (Example 3) should realize that the possibility he holds the wrong bunch is becoming more and more probable. On the other hand, he is not to blame for persisting in his attempts with the same bunch, because in each successive trial he is slightly more likely to succeed.
Suppose the police are scanning house after house in a given neighborhood in search of an escaped prisoner. The information that the runaway might be in the neighborhood was received from a source that is usually reliable. The police are right to become increasingly alert when moving from one house to the next. Their mounting apprehension, however, does not contradict the [pg362] assessment that the overall chances of finding the escapee in the neighborhood keep dropping as the search progresses unsuccessfully. These 2 apparently conflicting tendencies characterizes all situations where we sequentially search for an object in a given space, provided we lack complete certainty that it is there and the object is equally likely at the beginning to be in each unit of the space.
When waiting for an initially uncertain event to happen in consecutive time units, the long-term and short-range conditional probabilities of occurrence behave precisely as the respective hope functions in search situations. Thus, the geneticist (Example 4) was justified as time elapsed both in losing confidence that the Dean would call, and in hesitating to anesthetize another batch of flies. His feelings matched the course of the actual long-term and short-term probabilities of receiving the phone call.
Finally, the search (or wait) for Mr Right is roughly subject to the same apparently paradoxical rules. Patterns of nuptiality in several societies from about ages 18 to 30 indicate that although individuals who do not marry for several years are less likely ever to do so, their short-term conditional probabilities of marrying within a year keep rising for a while (Gabriel, 19606). The long-term and short-term functions describe the 2 faces of our optimism, or pessimism, depending on the desirability of the target event.
[See also the secretary problem. –Editor]
15.2 Subjective Hope
The ordinary person looking for some lost object instinctively holds to the scientific viewpoint…He is neither philosophically unmoved by the progress of the search, nor does his optimism rise increasingly as successive possibilities are eliminated. His initial cautious hope is increasingly balanced by the growing conviction, born of successive failures, that it’s not there, that it’s not anywhere: and when he regards this as adequately proven, he gives up. (Jones, 196660ya, page 466)
To find out whether Jones’ evaluation of the “ordinary person” is true, we asked subjects to answer the questions posed in Problems 1 and 2. The general question of whether people intuitively grasp the Bayesian solution can be decomposed into several more specific questions. To what extent is base-rate information (prior probability) taken into account? How is the ongoing failure to find the object incorporated into the reasoning? Do people correctly assess the direction of the 2 functions, namely, the simultaneous descent of the long-term hope (L) and ascent of the short-term hope (S)? Do they experience an intuitive conflict when trying to evaluate Si, sensing that that the general hope is decreasing but the diminishing number of remaining possibilities suggests that success in the next trial becomes more likely?
[pg363]
In addition to the numerical versions of Problems 1 and 2 given above, we composed directional versions of these examples which differed only in asking about directions instead of numbers. Thus, for example, question (1) in directional DL version asked whether the probability that the letter is in the desk is now greater than, equal to, or less than 80%. Question (2) asked whether the same probability is now greater than, equal to, or less than what it was in (2). The same was true for the directional DS version which asked in (1) whether the probability that the letter is in the next drawer is now less than, equal to, or greater than what it was for the first drawer. Question (2) asked for a comparison of the short-run probability with that of (1), and so on. Equivalent changes were introduced into the directional versions of BL and BS.
The design included 8 kinds of problems made up of all combinations of 3 binary variables: (1) story (desk or bus), (2) range (long or short), (3) question type (numerical or directional). 61 subjects—36 undergraduate students of psychology from the University of Massachusetts, Amherst, and 25 senior high-school students (of ages 17 & 18) from Massachusetts—answered 2 problems. The 2 forms each subject got differed on all 3 dimensions. Thus, a subject who first got directional BL would then receive numerical DS. Order of administration and all other aspects of design were counterbalanced. Subjects were instructed at the head of the form to read the problem carefully and trust their common sense in answering the questions. They were asked at the end to explain their reasoning.
15.2.1 Directional and Numerical Assessments
We first analyzed the data ordinally. Ignoring the exact values in the numerical versions, we sorted responses into 3 main types: strictly increasing, strictly decreasing, or a constant function. A 4th category (other) included functions which changed directions or were weakly monotonic. (The undergraduate and senior high-school students’ responses were pooled since the pattern of responses of the 2 groups were very similar.) Table 15.3 shows the 2-dimensional distribution, pooled across story types, of the 61 subjects according to the kind of L and S functions which they produced.
The results in Table 15.3 show that a majority of the subjects (35) intuitively sensed the decline of the L function. The modal group of subjects (27) produced an increasing S function. Yet, only about one fifth of the subjects (12) generated the correct combination of a decreasing L and an increasing S function. It is noteworthy that in a pilot study with 42 undergraduate law students at the Hebrew University of Jerusalem, about one fifth (8) produced the correct combination. The pilot study used different but isomorphic stories [pg364] (searching an escaped prisoner in successive houses, and waiting for a forgetful professor to come to an appointment).
Table 15.3
Subjects classified according to the long-term and short-term hope functions they produced [columns 2–4 for “Long-run hope”]
Short-run hope |
Increasing |
Decreasing |
Constant |
Other |
Total |
|---|---|---|---|---|---|
Increasing |
– |
12 |
11 |
4 |
27 |
Decreasing |
– |
7 |
1 |
1 |
9 |
Constant |
– |
6 |
7 |
1 |
14 |
Other |
– |
10 |
– |
1 |
11 |
Total |
– |
35 |
19 |
7 |
61 |
None of the 61 subjects responded with a correct triplet of numerical probabilities to any of the L or S forms. This was true for all the numerical versions and for many of the directional versions in which subjects gave numerical answers while explaining their choices. Overall, it is clear that students of fairly high ability are incapable of correctly assessing the L and S hope probabilities, but they have a rudimentary conception of the correct directions of the 2 functions.
15.2.2 Principal Assumptions Underlying Solution Strategies
Solution strategies are suggested by the pattern of subjects’ numerical responses and the explanations they provided. In examining these, a few heuristics appear to us to be guiding a substantial number of responses. In particular, in many cases assumptions of constancy underlie the choice of the 3 answers.
Suppose one assumes that the given L0 of 0.80 in Problem 1 (desk) stays unchanged despite failing to find the letter in the first i drawers. That assumption, which we label constant L, entails an identical response of 0.80 to all questions of DL and an increasing triplet of answers to DS—(1) 0.114 (ie. 0.80/7), (2) 0.20, (3) 0.80 (see the correct set of answers in Table 15.1). One may, however, assume that the probability of success per drawer (unit) stays unchanged. We label that assumption constant S. It entails an identical response of 0.10 (ie. S0) to all the questions in DS and a decreasing triplet of answers to DL—(1) 0.70, (2) 0.40, (3) 0.10 (cf. Table 15.1). The corresponding predictions of responses to BL and BS under the 2 constancy assumptions can be easily obtained.
The responses of 12 subjects to the 2 forms were compatible with the constant L assumption. 6 subjects assumed constant S across both forms, [pg365] and another 13 assumed constant L in answering one form and constant S in the other. Among the remaining 30 subjects, 19 assumed constancy in only one of the forms (6 constant L, and 13 constant S). Overall, of the 122 forms answered by 61 subjects, 81 (ie. 66.4%) were based on constancy assumptions: 43 constant L, and 38 constant S.
The heuristic of adhering to one constant parameter of the setup (whether L0 or S0) reduces the complexity of the hope problems. But it may also reflect subjects’ conception of probability as an unchanging propensity of the situation at hand. 1982 draw a distinction between 2 loci to which uncertainty can be attributed: the external world or our state of knowledge. Real-world systems are frequently perceived as having dispositions to produce different events, and the probabilities of these events are judged by assessing the strength of these dispositions. The propensity of the desk (or drawer) to produce the missing letter (or, for that matter, of the transportation system to produce the bus) may have been considered a fixed parameter of the setup by many of our subjects. This would explain why they refused to update that parameter in light of the accumulating search results. They did not interpret the question as addressing their state of knowledge, and were consequently impervious to the effect of new evidence.
Subjects often explicitly expressed the idea that constant probability was a characteristic disposition of the chance setup. The following statements were made by subjects who responded invariably with an answer of 80% to all the questions in numerical DL: “The probability that the letter is in the desk is 80%, and that’s it!” A deliberate attempt to ignore the information about successive failures (as if the subject is wary of falling prey to the gambler’s fallacy) is notable in another subject’s words: “Like the lottery, no matter how many times you play or what number you use, you have the same probability in winning. So each desk has an 80% chance of having the letter.” Similar insistence on the irrelevance of the reported outcomes is found in: “Finding empty drawers doesn’t change probability that letter is in desk”, and “The letter is equally likely (80%) to be in any of the drawers—so the fact that x number of drawers was checked does not lower the probability.”
The constancy of the long-run hope for the arrival of the bus (Problem 2) was justified by “I figure that the exact time between 11:30 and 12:00 (11:35, 11:45, 11:55) doesn’t really matter—since 60% of the buses operate this late I think there is still a 60% chance that a bus will come.” However, the same subject assumed constancy per unit when asked about short-term probabilities: “Since there are 8 drawers and the letter, if it is any of the drawers, is equally likely to be in any of the drawers, the probability that the letter is in any one drawer is 10%. This doesn’t change if the letter is not in one or more of the other drawers [italics added].” Had this discussion taken place in class, the teacher could have asked at that point, “and what if the letter is found in the _i_th drawer, would you still think the probability doesn’t change?”
[This kind of error could be considered a version of E.T. Jaynes’s mind projection fallacy (LW wiki); see 1989 paper “Probability Theory as Logic” or “Clearing up Mysteries—The Original Goal”. –Editor]
[pg366]
Assuming constant S when answering numerical BL, results in a decreasing _L function ((1) 50%, (2) 30%, (3) 10%). This was typically justified by answers such as: “I estimated that since there was 60% chance that the bus was still running…the chance of it arriving decreased by 10% as each 5 minute (of 6) passed.” Another subject’s explanation repeats the same rationale for DL: “There is 80% chance of letter in desk and 20% not. Checking one drawer with an unsuccessful try drops your chances of it being there by 10%, to 70%, and so on.”
In terms of the issue of “Evidential Impact of Base Rates” (the title of a paper by Tversky & Kahneman, 19827), an assumption of constant L represents an extreme point of “conservatism” on the continuum of use versus neglect of base-rate data. In fact, constant L is the reverse of the “base rate fallacy” according to which subjects typically ignore the base rate and consider only the specific evidence about the case in hand (as in Tversky & Kahneman’s well-known cab problem). The constant S assumption, although resulting in exaggerated decrease of the L function, keeps the base-rate unit unchanged instead of duly increasing it in light of the evidence. In this sense, constant S is conservative as well.
Our impression is that subjects’ conservatism, as revealed by the prevalence of the constancy assumptions, is a consequence of their external attribution of uncertainty (Kahneman & Tversky, 198244ya). The parameters L0 and/or S0 are apparently perceived as properties that belong to the desk, like color, size and texture. Subjects think of these parameters in terms of “the probabilities of the desk”, whereas the Bayesian view would imply expressions like “my probability of the target event”. Thus, subjects fail to incorporate the additional knowledge they acquire when given successive search results.
15.2.3 Other Strategies
Several subjects denied the presence of chance altogether and acted as if it were certain that the letter was in the desk (the bus is going to come), and others embraced the historic position of equal ignorance and responded with “fifty-fifty”, in apparent disregard of the givens of the problem.
Eleven subjects relied on assumption of certainty in response to one of the problems they answered. Another 3 subjects assumed certainty in both problems. Most of the certainty-based responses were made by subjects assuming either constant L or constant S. Thus, for example, assuming initial certainty and constant S when responding to numerical BL means that S0 = 17% = 1⁄6, and that S0 is subtracted from the L function (starting with L0 = 100%) for every 5-minute interval in which the bus does not arrive. This results in: (1) 83%, (2) 50%, (3) 17%. One subject justified this triplet as follows: “I made a time table of 30 minutes. I take a fraction of how much time has elapsed, then divide by 100%, giving the answer.” Note that this [pg367] subject was not disturbed by the fact that probability of 83% following a 5-minute wait for the bus was higher than the given initial probability of 60%.
The double assumption of initial certainty and constant L means that L0 = 100% stays unchanged. Thus, when answering numerical DS, these 100 percents are divided each time in equal shares among the remaining drawers, resulting in (1) 14% = 1⁄7, (2) 25%, (3) 100%. We quote one subject’s elaborate justification of the above triplet: “If you didn’t eliminate drawers and randomly pointed to any drawer there would be still 1⁄8 probability because there is replacement. But here we don’t have any replacement and each drawer is equally likely of containing the letter, so however many drawers you have it’s 1⧸N probability.”
No less surprising than the responses that converted the initial probability of 80% (or 60%) into certainty were those that assumed total ignorance and concluded therefore that the target probability should be one half. 10 subjects appeared to invoke the maxim of “insufficient reason” assigning equal probabilities to the 2 possible outcomes. Consider the explanation of a subject who gave a constant 50% answer to all 3 BS questions: “Because since you don’t have any idea what time the bus arrives and you don’t even know if the bus is coming, then it is equally likely to arrive at any time.” Another subject, who responded similarly, wrote: “It doesn’t matter that the bus didn’t arrive in the last 5 minutes. There is always a 50% chance it will come an a 50% chance it will not come.” A uniform 50% response to the 3 BL questions was explained by: “There is no ↑ in probability it will come because there’s only 5 min left—there’s still a 50:50 chance it will either come or its doesn’t.” One subject’s “ingenious” reasoning with respect to BL resulted in: (1) 41.6%, (2) 25%, (C) 8.3%. His telegraphic-style explanation ran as follows:
6 5 min intervals from 11:30–12:00
- said it was =ly likely at 11:30 (50%)
50%:6 = 8.3
each 5 min interval decreases probability by 8.3%
We see here an interesting combination of the equal-ignorance and constant-S heuristics.
The human tendency to remove chance from our considerations has been observed in various judgmental contexts (several examples are reviewed by Falk & Konold, 19928). The same is true for people’s inclination to assume equal likelihood once uncertainty is acknowledged. The tendency to identify randomness with equiprobability and thus assign equal chances to the available options has been widely documented in empirical investigations (eg. et al 19919; Shimojo & Ichikawa, 1989). The primacy of the equiprobability intuition has been described in studies of the historical [pg368] development of probability theory. Uniformity was the first presumption on which probability calculations were based ( et al 198910; Hacking, 197511, Chapter 14). Converging evidence thus testifies to the genuine power of the intuitive bent toward symmetry (Falk, 1992; Zabell, 1988).
Paradoxically, subjects’ assumptions of certainty and of equal ignorance, although diametrically at odds with each other, might be viewed as the 2 Janus-faces of the same orientation. Konold (198937ya) has referred to that orientation as the outcome approach. People reasoning via the outcome approach tend to interpret a request for a probability of some event as a request to predict whether or not that event will occur on the next trial. Contrary to current scientific thinking, these reasoners do not view probability as a measure of one’s uncertainty, nor as answering the question about the relative frequency of occurrence of the target event in many repeated trials. According to Konold’s (198937ya) description, outcome-oriented subjects translate probability values into yes/no decisions, transforming their probability evaluations into certainty. Thus, a probability of 20% means “it won’t happen”, a probability of 80% means “it will happen”. When they sense a total lack of knowledge about the outcome, however, they express it by the 50:50 numerical probability, which means “it either will happen or won’t happen—don’t know which”. Konold found in several studies that a certain subgroup of the subjects (not necessarily a majority) was fairly consistent in responding according to this outcome-oriented perspective.
Although we cannot predict whether an outcome-oriented subject would convert the probabilities given in our problems into certainty or into equal ignorance, it stands to reason that the former would occur more often when the probabilities are close to 100% (or to zero) and the latter when the probabilities are close to 50%. Our data show roughly this pattern. Of the 17 forms which elicited certainty-based responses, 10 were desk problems (L0 = 80%) and 7 bus problems (L0 = 60%). In contrast, of the 10 equally likely answers, 3 were given in response to the desk story and 7 to the bus. These include 2 subjects who responded by certainty to the desk and by equal ignorance to the bus. Overall, the conjecture that the outcome approach has played some role in answering the hope problems is weakly supported. It remains a possibility that should be further explored.
15.2.4 Toward a Solution
It was somewhat surprising that we did not find among the explanations of the S problems an explication of the conflict between the diminishing long-term hope and the increasing immediate hope implied by the fewer remaining units. One subject who produced a constant S function in response to directional BS [pg369] did describe another conflict: “The probability that the bus will arrive in any given time slot is the same. Although my intuition would urge me to expect to see the bus more (meaning—I would assume the probability would be greater) as time elapsed, I believe that the ‘laws’ of probability would have it otherwise. But—as I think about it more, this could be argued against, saying that the probability changes as each unknown 5-minute segment became known.” Several subjects, who produced a decreasing L function in response to directional versions (without giving numbers), gave a correct Bayesian-like explanation (eg. “Well, if it is not in a drawer, then it could fall in the 20% zone and the more drawers you open without it being in there the lower the probability that it’s in there”).
Only one subject (No. 62), a pre-college student enrolled at the Hebrew University of Jerusalem, responded correctly to both problems, in this case to numerical BL and directional DS.
BL:
At 11:30 the probability of the bus arriving by midnight was 6⁄10, and of not: 4⁄10
At 11:35 the probability of the bus arriving by midnight was 5⁄9, and of not: 4⁄9
At 11:45 the probability of the bus arriving by midnight was 3⁄7, and of not: 4⁄7
At 11:55 the probability of the bus arriving by midnight was 1⁄5, and of not: 4⁄5
DS:
At the beginning of the search the letter could be in one of 10 “locations”: 8 drawers and 2 “others”. The 2 “others” stay in constant amount, whereas the number of drawers keeps decreasing. Therefore, the chance of finding the letter in the first drawer was only 10% (ie. 1⁄10), in the second 1⁄9, in the fifth 1⁄6 and in the 8th 1⁄3.
These considerations yielded the same results (for each i) as the Bayesian computations. Note, however, that whenever several units are eliminated, the posterior probability distribution over the remaining units (including the imaginary “other” locations) stays uniform. That is why this subject’s reasoning matched the Bayesian results. The same method would not work if applied to problems like that of the 3 prisoners, or Monty’s notorious TV game “Let’s make a deal” (Falk, 199234ya).
Inspired by that subject’s method of solution, we devised a simplified version of the desk problem. The main change in the modified version was the addition of a concrete representation of the sample space that includes the 2 “locations” out of the desk.
[pg370]
15.3 The Hope Problem—Simplified
The simplified desk problem, presented below, is isomorphic to Problem 1:
Problem 1R The Revised Desk Problem. (Revised-Desk-Long—RDL; Revised-Desk-Short—RDS). The problem stem of both RDL and RDS reads as follows:
Imagine that you are searching for an important letter that you received some time ago. Your assistant always puts your letters in the drawers of your desk after you have read them.
There are 10 drawers in your desk. You know that the letter is equally likely to be in any of the 10 drawers. You notice, however, that drawers #9 and #10 are locked (see figure), and your assistant has gone home with the keys. You realize the chances that the letter is in one of the unlocked drawers is 80%. So you start a thorough and systematic search of the 8 unlocked drawers.
Figure 15.2 presents the drawing which appeared in each form. The 3 questions in RDL were the same as in DL of Problem 1, except they asked for an evaluation of the probability that the letter is in one of the unlocked drawers. RDS included exactly the same questions as DS of Problem 1. Only numerical revised forms were prepared.
Figure 15.2
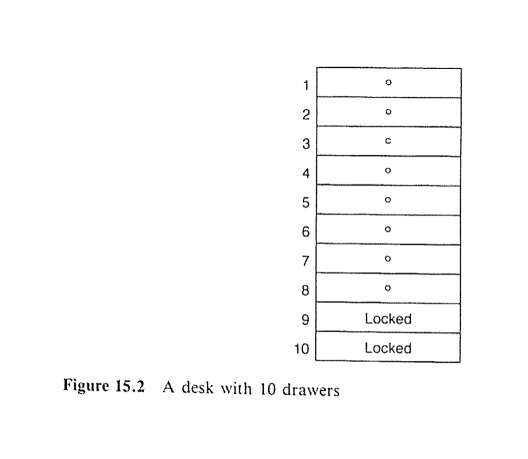
A desk with 10 drawers
A pilot test was run at the University of Massachusetts, Amherst with 13 subjects (including graduate and postgraduate students). Each subject responded to only one form: 6 to RDL and 7 to RDS. 3 of the responses to RDL and 6 of the responses to RDS were perfectly correct. Of the other [pg371] 3 RDLs, subjects gave 2 constant L responses and 1 constant S response. The 7th RDS answer assumed constant L.
Based on the results of this pretest, we conducted larger-scale surveys. Our aim was both to confirm the indications that the revised versions facilitate reaching the correct solution and to test whether subjects who succeed in solving Problem 1R would transfer the solution principle to the Standard Wait Problem (Problem 2) as originally phrased.
Fifty-four subjects—34 undergraduate psychology students from the University of Massachusetts, Amherst and 20 senior high-school students from Massachusetts—participated in the first survey. Each subject was asked to answer 2 problems: either RDL and numerical BL, or RDS and numerical BS. The revised desk problem was always given first; 26 subjects received 2 L versions and 28 received 2 S versions.
Eighteen of the 54 revised forms were answered correctly (9 RDLs, and 9 RDSs). Compared with no correct answers to numerical DL and DS in the original group of 61 subjects, the rise to 33.3% correct represents a “dramatic” improvement. The 36 incorrect responses to the revised forms included 14 based on constancy assumptions (12 constant S and 2 constant L), 2 based on certainty and based on equal ignorance (ie. 50:50).
None of the 54 bus problems were answered correctly, indicating no transfer of the solution strategy by those 18 subjects who have just solved a search problem (desk). Incorrect responses included 26 constancy-based answers (20 constant S and 6 constant L), 10 certainty and 5 equal ignorance.
Correct answers to the revised desk problem were often accompanied by lucid explanations of the underlying reasoning. here is one example given in response to RDL: “The probability that I gave is the number of unlocked drawers remaining (unsearched) divided by the total number of drawers remaining (unlocked+locked).”
Similar to the explanations of incorrect answers to Problem 1, a constant 80% answer to RDL was justified by: “The overall probability doesn’t change no matter how many drawers are searched”, and, as maintained by another subject: “regardless of whether I looked in them or not.” Some subjects who responded 80% throughout seemed to work hard not to be swayed by the given results: “It’s like the boy/girl baby problem, even if you get BBBBBBBBBG the probability still remains at chance—50:50.” Constant S responses to RDL were justified by, “I was almost fooled, but upon further thought I decided that as drawers are searched and found empty the statistics of the problem do not change. Same as if weather person says 50% chance of rain & it rains. Then is probability of rain 50% or 100%? It’s still 50%.” One subject, who gave 50% answers to RDS, explained: “The possibility of finding the letter was 50%, just like yes or no.”
In a second survey, each subject received RDL and RDS, with order of presentation counterbalanced, and a bus problem of the same range (L or S) [pg372] as the second of the 2 revised problems. The 109 subjects were undergraduate students of psychology or graduate students of education at the Hebrew University of Jerusalem. 53 got RDS, RDL, BL, in that order, and 56 got RDL, RDS, BS. Because of the extra length of this assignment subjects were not asked to explain their reasoning.
Correct responses were given to 48 of the 109 RDLs (44%), and to 73 out of 109 RDSs (67%), which is 56% correct overall. Every subject who correctly solved RDL correctly solved RDS as well, but not vice versa, suggesting that the revised short-term problem is more transparent. This makes sense if one notes that answering the S versions involves adjustment of only the denominator (the total number of remaining units) since the numerator is always one, whereas answering the L versions requires adjustment of both numerator and denominator. Assumptions of constancy, certainty, and equal ignorance were observed among the incorrectly answered forms. However, the absence of supporting explanations prevented a determination of subject’s underlying reasoning.
No single correct triplet of answers was given to any of the 109 bus problems. This was true despite the high rate of correct solutions of the immediately preceding revised desk problems. In particular, 68 of 109 subjects solved their second revised desk problem but not the equivalent bus problem of the same range. In conclusion, while the revised desk problems elicited more than half correct solutions, transfer of the method of solution to the bus problem failed to occur.*
15.4 Discussion
On the whole, subjects were unable to solve the numerical long-term and short-term hope problems the way they were originally presented. To summarize our findings, we list several solution methods that subjects employed and beliefs they expressed. To be sure, this list is not exhaustive.
The load of processing the various details given in Problems 1 and 2 is eased if one of the givens (either L0 or S0, which is inferred from L0) is held constant. Many subjects indeed based their answers on one of these constancy assumptions, solving the problem by reducing the number of variables involved. In so doing, they ignored one type of evidence, namely the search results, and considered only the a priori success probability and sometimes also the number of units.
Subjects’ choice of the type of evidence may be linked to an external attribution of uncertainty. Many of the explanations cited above indicate that the prior was viewed as an inherent and unalterable characteristic of the setup. It may seem more “objective” than the information about the subsequent fruitless search (wait), and may therefore come to dominate subjects’ reasoning.
[pg373]
Some subjects clearly resisted the urge to use epistemic considerations. The burden of providing the required probability, they insisted, should lie with the desk (bus system). We should note that all subjects had had some kind of introductory statistics course. Their cursory statistical knowledge apparently alerted them to the gambler’s fallacy. The first examples of random processes usually given in class (successive coin tosses, childbirths, lotteries, etc.) are typically characterized by statistical independence. Students learn that they should not learn from experience since a coin has no memory. This lesson may be overgeneralized to the case of the hope problems, where successive failures do have a diagnostic value.
Those subjects who were aware of the need to consider the changes in their state of knowledge usually sensed the direction of the hope functions but did not know how to update their probabilities arithmetically. The concrete aid offered in the revised desk problem helped many of these subjects to simultaneously see the whole sample space and the subspace in which success may occur.
Failures in responding to the revised versions occurred when subjects were strongly committed to constancy assumptions. Whoever believes that the probability of the letter is 10% per drawer, regardless of how many drawers have been searched, will fail to adjust for the changing total number of drawers and will simply obtain the L function by multiplying 10% by the number of unlocked drawers that have not yet been eliminated.
In addition, a certain subgroup of subjects who answered the original problems, and the revised desk problem, was apparently outcome oriented. They resorted either to certainty or to complete indifference, both of which resulted in incorrect answers.
15.4.1 Why Didn’t the Transfer Work?
We were puzzled by the failure of all the subjects who had solved the revised desk problem to transfer the solution’s rationale to the bus problem. However, on second thought, and as a result of post-experimental discussions with some of the subjects, we have one possible reason for this failure of transfer.
The solution in the revised version was suggested by extending the dimension along which the search was carried out: 2 units (drawers) were added so the subjects could visualize the whole sample space and see the reason for the a priori L0 of 80%. As they eliminated drawers, they could see the remaining “favorable” (unlocked) and “unfavorable” (locked) units of the changing space. When facing the bus problem, however, one cannot apply the same trick without changing the nature of the story. Extending the units of wait beyond midnight would not help to see the reason why L0 is 60%. That prior reflects the fact that 60% of the bus routes operate this late, and 40% do not. A revision, equivalent to that of the desk problem, would have the bus [pg374] certain to arrive sometime between 11:30 and 12:20, with equal probabilities for all the 10 5-minute intervals. The tourists, however, decide to wait until either the bus arrives or midnight, whichever happens first. Viewing the original bus problem as isomorphic to the revised desk problem was apparently too much to expect of subjects in an experimental situation.
The locked-drawers device can easily be applied to Dr Fischer’s bomb situation (Example 2). Without loss of generality, we can change the story so that there are 12 Christmas crackers: one contains a bomb for sure, 11 contain checks. Only 6, however, are at the guests’ disposal for this party. The other 6 are kept for the next party. It is now easy to see that L0 is 50% and to assess the L and S probabilities of pulling the bomb throughout the game’s progress. We didn’t pose this problem to our subjects. Our guess, however, is that transfer from the revised desk problem to this particular problem would have been within reach of some subjects.
15.4.2 Possible Extensions
Several subjects who viewed the search/wait process as analogous to coin flipping, incidentally raised an interesting equation: what if the search were to be conducted with replacement? Suppose the man who comes home in the darkness with 2 bunches of keys (Example 3) is drunk. He would not be able to remove keys that have failed to unlock the door (see Feller, 195769ya, page 46). Or, imagine that an absent-minded professor is looking for a misplaced letter through the drawers of her desk (Problem 1) while her mind is deeply engaged in some other problem, thus forgetting instantaneously which drawers have been already searched. A “with replacement search” thus describes the case in which a key may be tried again after being found not to work or a drawer may be searched again after being found empty.
Does it make sense to think of waiting for the bus “with replacement”? Ennis (198541ya)12 describes a situation perfectly suited for our case. He imagines
waiting for a bus on a route which offers a “15-minute service”. Because of heavy traffic, the buses do not arrive at exactly 15-minute intervals but randomly. The operators (Poisson Motor Services) do, however, provide a service which averages out at 15 minutes between buses. (page 27)
We only need to change 15 to 30 minutes, add the qualification that the chances are 60% that the bus is running that late, and Poisson Motor Services provide us a wait problem with replacement.
The computation of the long-term (L’) and the short-term (S’) hope functions for sampling with replacement requires a minor adjustment of [pg375] formulas (15.1) and (15.2). One easily obtains, for the case of sampling with replacement:
(15.1’)
(15.2’)
S’i = 1⧸n × L’i
In both formulas i = 0, 1, 2, …, n − 1, n, …
In contrast to the case of sampling without replacement, where the function Li decreases with i and Si increases (Figure 15.1), in the case of sampling with replacement, both L’i and S’i decrease. The rate of their decline, however, is slower than that of Li. Figure 15.3 presents the course of the functions L’i and S’i compared with that of Li and Si, for the desk problem. In the limit, as i grows indefinitely, both L’i and S’i tend to zero. This means that despair creeps in justifiably in an extended fruitless search (wait) with replacement. In a without-replacement search, the rising S function may boost our morale to some degree. it is probably the short-range increase in hope that keeps most of us going.
Figure 15.3
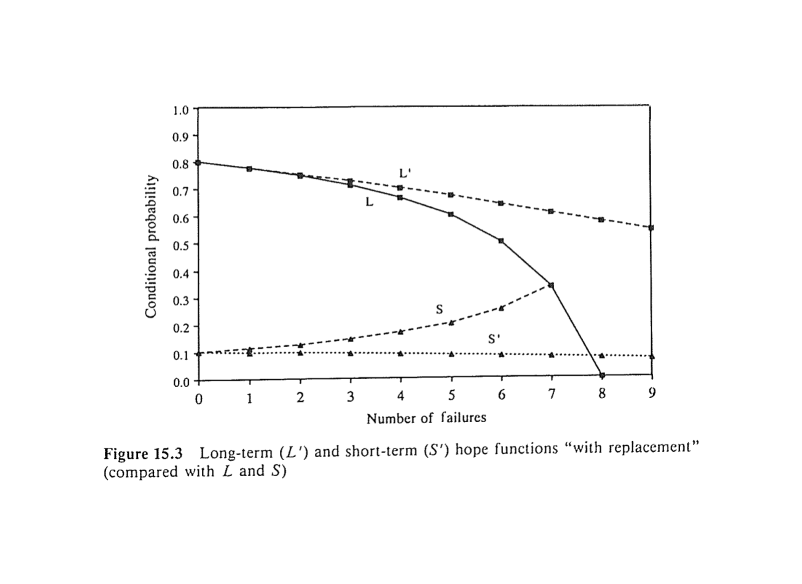
Long-term (L’) and short-term (S’) hope functions “with replacement” (compared with L and S)
Another extension of the original probability model is obtained if in Problem 1 we allow for a less than perfect search. One may assume, for instance, that the conditional probability of finding the letter in a drawer, given it is there, is always p (such that 0<p < 1). This would, in fact, describe more realistically the state of affairs in desks of people like ourselves. In [pg376] addition to that, one may monitor the course of the hope functions while searching within each drawer. This will amount to extending the problem from the discrete to the continuous case.
Decisions of whether to continue or end a search (wait) depend not only on the long-term and short-term success probabilities. The considerations should include the costs and benefits associated with each decision. These, however, may change as the search proceeds.
Note that our search and wait problems involved desirable outcomes. The desirability of the target event makes no difference formally. It would be interesting to see, however, whether people’s subjective functions, based on the same objective statistics, differ in any way when viewing the target event as “success” versus “failure”. Clearly, picking one of 2 bunches of keys (Example 3) and trying them successively with or without replacement, is isomorphic to picking one of 2 guns, knowing that there is a bullet in one of them, and playing Russian Roulette with or without replacement. The “target” event, however, is so dramatically different in these 2 cases, that finding differences in probabilistic assessments would not be surprising. Likewise, waiting for malignant symptoms to reappear during a 5-year period after treatment, although structurally equivalent to waiting for your loved one to come to a date during 5 successive short-time intervals, may be evaluated differently in probabilistic terms. Clearly, continued study of these phenomena is required.
Acknowledgments
Part of the research described in this chapter was carried out while the first 2 authors were at the Department of Psychology at the University of Massachusetts, Amherst. The study was supported in part by the National Science Foundation grant MDR-8954626 to Clifford Konold, and in part by the Sturman Center for Human Development, The Hebrew University, Jerusalem. We are grateful to Arnie Well, Sandy Pollatsek, and Jill Lohmeier for preliminary discussions concerning this project, to Dorit Rivkin and Oren Gilady for conducting pilot tests and raising suggestions, to Peter Ayton for contributing engaging examples, and to Oren Falk for being the first to solve the hope problems by common sense. Many of our students, who acted as subjects, have enriched our understanding by their comments and discussions.
Special thanks are due to Raphael Falk, who has devotedly helped us in all the stages of the study: developing concepts, identifying examples, and writing it up.
External Links
“Waiting for the bus: When base-rates refuse to be neglected”, 2007:
The paper reports the results from 16 versions of a simple probability estimation task, where probability estimates derived from base-rate information have to be modified by case knowledge. In the bus problem [adapted from Falk, R., Lipson, A., & Konold, C. (199432ya). “The ups and downs of the hope function in a fruitless search”. In G. Wright & P. Ayton (Eds.), Subjective probability (pp. 353–377). Chichester, UK: Wiley], a passenger waits for a bus that departs before schedule in 10% of the cases, and is more than 10 min delayed in another 10%. What are Fred’s chances of catching the bus on a day when he arrives on time and waits for 10 min? Most respondents think his probability is 10%, or 90%, instead of 50%, which is the correct answer. The experiments demonstrate the difficulties people have in replacing the original 3-category 1/8/1 partitioning with a normalized, binary partitioning, where the middle category is discarded. In contrast with typical studies of “base-rate neglect”, or under-weighing of base-rates, this task demonstrates a reversed base-rate fallacy, where frequentistic information is overextended and case information ignored. Possible explanations for this robust phenomenon are briefly discussed.
“The allure of equality: Uniformity in probabilistic and statistical judgment”, 2008:
Uniformity, that is, equiprobability of all available options is central as a theoretical presupposition and as a computational tool in probability theory. It is justified only when applied to an appropriate sample space. In 5 studies, we posed diversified problems that called for unequal probabilities or weights to be assigned to the given units. The predominant response was choice of equal probabilities and weights. Many participants failed the task of partitioning the possibilities into elements that justify uniformity. The uniformity fallacy proved compelling and robust across varied content areas, tasks, and cases in which the correct weights should either have been directly or inversely proportional to their respective values. Debiasing measures included presenting individualized and visual data and asking for extreme comparisons. The preference of uniformity obtains across several contexts. It seems to serve as an anchor also in mathematical and social judgments. People’s pervasive partiality for uniformity is explained as a quest for fairness and symmetry, and possibly in terms of expediency.
“The Hope Function”, Sam Alexander
applying the Hope Function to technological forecasting (but it could also be applied to politics)
of Artificial Intelligence; this initial analysis loosely inspired material in “Intelligence Explosion: Evidence and Import” (2012), pg5:
How, then, might we predict when AI will be created? We consider several strategies below. By considering the time since Dartmouth. We have now seen more than 50 years of work toward machine intelligence since the seminal Dartmouth conference on AI, but AI has not yet arrived. This seems, intuitively, like strong evidence that AI won’t arrive in the next minute, good evidence it won’t arrive in the next year, and substantial but far from airtight evidence that it won’t arrive in the next few decades. Such intuitions can be formalized into models that, while simplistic, can form a useful starting point for estimating the time to machine intelligence.8
8: We can make a simple formal model of this evidence by assuming (with much simplification) that every year a coin is tossed to determine whether we will get AI that year, and that we are initially unsure of the weighting on that coin. We have observed more than 50 years of “no AI” since the first time serious scientists believed AI might be around the corner. This “56 years of no AI” observation would be highly unlikely under models where the coin comes up “AI” on 90% of years (the probability of our observations would be 10-56), or even models where it comes up “AI” in 10% of all years (probability 0.3%), whereas it’s the expected case if the coin comes up “AI” in, say, 1% of all years, or for that matter in 0.0001% of all years. Thus, in this toy model, our “no AI for 56 years” observation should update us strongly against coin weightings in which AI would be likely in the next minute, or even year, while leaving the relative probabilities of “AI expected in 200 years” and “AI expected in 2 million years” more or less untouched. (These updated probabilities are robust to choice of the time interval between coin flips; it matters little whether the coin is tossed once per decade, or once per millisecond, or whether one takes a limit as the time interval goes to zero.) Of course, one gets a different result if a different “starting point” is chosen, eg. Alan Turing’s seminal paper on machine intelligence (1950) or the inaugural conference on artificial general intelligence (Wang, Goertzel, and 2008). For more on this approach and Laplace’s rule of succession, see Jaynes (200323ya), chapter 18. We suggest this approach only as a way of generating a prior probability distribution over AI timelines, from which one can then update upon encountering additional evidence.
the Lindy effect
“The Inspection Paradox is Everywhere”; “The Waiting Time Paradox, or, Why Is My Bus Always Late?”; “NYC Subway Math”, Erik Bernhardsson
“Searching for keys in a desk”, Max Stockslager
Bell, C.R. (197947ya) “Psychological aspects of probability and uncertainty”. In C.R. Bell (ed.), Uncertain Outcomes, MTP Press, Lancaster, England, pages 5–21.↩︎
Jones, D.E.H. (196660ya) “On being blinded with science”. New Scientist, November, 465–7.↩︎
Feller, W. (195769ya) An Introduction to Probability Theory and its Applications, Vol. 1 (2nd edition). Wiley, New York.↩︎
Meshalkin, L.D. (197353ya) Collection of Problems in Probability Theory (L.F. Boron & B.A. Haworth, trans.) Noordhoff, Leyden, The Netherlands (Original work published 196363ya).↩︎
Falk, R. (199333ya) Understanding Probability and Statistics: A Book of Problems. AK Peters, Wellesley, Ma.↩︎
Gabriel, K.R. (196066ya) Nuptiality and Fertility in Israel. Doctoral dissertation (in Hebrew with English summary). The Hebrew University, Jerusalem.↩︎
Tversky, A. & Kahneman, D. (198244ya) “Evidential impact of base rates”. In D. Kahneman, P. Slovic & A. Tversky (eds.), Judgement under Uncertainty: Heuristics and Biases. Cambridge University Press, Cambridge, pages 153–60.↩︎
Falk, R. & Konold, C. (199234ya) “The psychology of learning probability”. In F.S. Gordon & S.P. Gordon (eds.), Statistics for the Twenty-First Century. The Mathematical Association of America, USA, pages 151–64.↩︎
Konold, C., Lohmeier, J., Pollatsek, A., Well, A., Falk, R. & Lipson, A. (199135ya) “Novice views on randomness”. Proceedings of the 13th Annual Meeting of the International Group for the Psychology of mathematics Education—North American Chapter, 1, 167–73.↩︎
Gigerenzer, G., Switjink, Z., Porter, T., Daston, L., Beatty, J. & Krueger, L. (198937ya) The Empire of Chance: How Probability Changed Science and Everyday Life. Cambridge University Press, Cambridge.↩︎
Hacking, I. (197551ya) The Emergence of Probability. Cambridge University Press, Cambridge.↩︎
Ennis, J. (198541ya) “Statistics, St Petersburg and Sellafield”. New Scientist, May, 26–28.↩︎