Caffeine wakeup experiment
Self-experiment on whether consuming caffeine immediately upon waking results in less time in bed & higher productivity. The results indicate a small and uncertain effect.
One trick to combat morning sluggishness is to get caffeine extra-early by using caffeine pills shortly before or upon trying to get up. From 2013–201412ya I ran a blinded & placebo-controlled randomized experiment measuring the effect of caffeine pills in the morning upon awakening time and daily productivity. The estimated effect is small and the posterior probability relatively low, but a decision analysis suggests that since caffeine pills are so cheap, it would be worthwhile to conduct another experiment; however, increasing Zeo equipment problems have made me hold off additional experiments indefinitely.
With the coming of winter, I, like so many other people, have started to find sleeping in to be too tempting: why get out of bed into the cold air when I can just snuggle under my covers and drowse another hour? This is bad because I was getting sufficient sleep as it was and didn’t need more, and because I think it may exacerbate sleep inertia as the waking process is dragged out for a long time. All in all, the days seemed less productive and drearier whenever I crawled out of bed an hour later than usual.
Then I was reminded by Kaj Sotala of an Anders Sandberg blog post I’d seen a while back, “The Early Bird gets the Caffeine Pill”:
I set my alarm to 6:00 and 8:00. At 6:00 I go up, take a 50mg caffeine pill, and go to bed again. Then I sleep and wake up rested and energetic around 8. In my case the time for the pill to start working seems to be 1.5 hours. A dose of one pill ensures that I wake up (but still yawning) while two pills makes me start the day much more quickly. The added benefit is of course a regular sleep schedule.
It sounds logical enough (why wouldn’t a caffeine pill work?), and he cites a study successfully trying a similar trick with naps. I’d meant to try it out at some point, and winter was as good a reason as any. I already had an ample supply of caffeine pills (technically, piracetam+caffeine+others), so I had just been procrastinating on doing a design & setting up my usual RCT. I decided that I might as well try it out as a simple easy non-blinded quasi-experimental alternate-day pilot experiment and if I felt like it after a month or two of data, I might try an RCT.
So on 2013-11-04, I started keeping a little jar of my caffeine+piracetam pills by my bedside and using them on alternate days (specifically, my Zeo SmartWake fires in the 9-9:30AM window and I take it then, while I may or may not snooze on). I stopped around April 201412ya.
Pilot Analysis
The correlational data shows a 15-20 minute difference in rise-time between caffeine & non-caffeine days.
First, does morning caffeine affect total sleep or time awake? I wouldn’t expect so, since it’s aimed at reducing morning wakefulness:
zeo <- read.csv("https://gwern.net/doc/zeo/2014-06-28-gwern-zeodata-caffeinecorrelation.csv")
zeo$Morning.Caffeine <- as.logical(zeo$Morning.Caffeine)
wilcox.test(Total.Z ~ Morning.Caffeine, data=zeo)
#
# Wilcoxon rank sum test with continuity correction
#
# data: Total.Z by Morning.Caffeine
# W = 2244, p-value = 0.7168
# alternative hypothesis: true location shift is not equal to 0
wilcox.test(Time.in.Wake ~ Morning.Caffeine, conf.int=TRUE, data=zeo)
#
# Wilcoxon rank sum test with continuity correction
#
# data: Time.in.Wake by Morning.Caffeine
# W = 2090, p-value = 0.7623
# alternative hypothesis: true location shift is not equal to 0
# 95% confidence interval:
# -5 3
# sample estimates:
# difference in location
# -1We should be able to see a shift in rise or wake time to an earlier time:
## convert "05/12/2014 06:45" to "06:45"
zeo$Rise.Time <- sapply(strsplit(as.character(zeo$Rise.Time), " "), function(x) { x[[2]] })
## convert "06:45" to 24300
interval <- function(x) { if (!is.na(x)) { if (grepl(" s",x)) as.integer(sub(" s","",x))
else { y <- unlist(strsplit(x, ":"));
as.integer(y[[1]])*60 + as.integer(y[[2]]); }
}
else NA
}
zeo$Rise.Time <- sapply(zeo$Rise.Time, interval)
## `hist(zeo$Rise.Time)` looks normally distributed, but there's a big outlier, so we'll use a U-test:
wilcox.test(Rise.Time ~ Morning.Caffeine, conf.int=TRUE, data=zeo)
#
# Wilcoxon rank sum test with continuity correction
#
# data: Rise.Time by Morning.Caffeine
# W = 2705, p-value = 0.01863
# alternative hypothesis: true location shift is not equal to 0
# 95% confidence interval:
# 5 40
# sample estimates:
# difference in location
# 20A definite hit! Rising 20 minutes earlier seems like a plausible estimate, too. Let’s take a look at the graph of rise-time over time:
zeo$Sleep.Date <- as.Date(zeo$Sleep.Date, format="%m/%d/%Y")
library(ggplot2)
qplot(Sleep.Date, Rise.Time, color=Morning.Caffeine, data=zeo)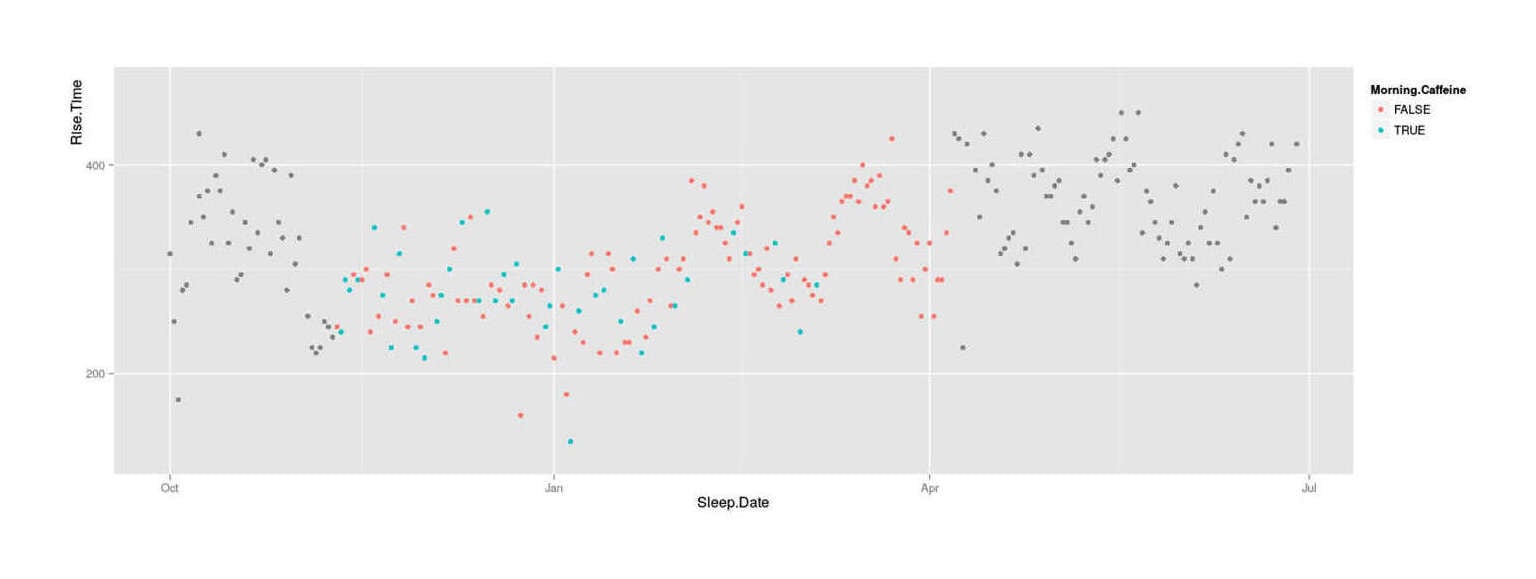
What time I got up in the morning, November–June 201412ya; colored by whether affected by a caffeine wake-up pill
Two observations immediately jump out:
the blue points (caffeine-affected) do seem to generally be below the red points (caffeine-free) and the U-test’s claim is believable
there seem to be very distinct temporal patterns, which make any correlations or analysis treacherous: before/after experiments will be worthless since they will sample from distinct periods of rising-time, so an experiment should definitely be blocked as pairs-of-days to minimize the clear drift or sinusoidal pattern.
A more precise analysis with covariates is possible; for example, depending on how late I went to bed, that might affect when I get up in the morning. But you have to be careful in what you look at - if you look at something like ‘total sleep length’, well, that’s partially caused by sleeping in! It must be impossible for the variables to be affected by sleeping in or not. So, Total.Z, Time.in.REM, etc. are all out as covariates (at least, without digging into the time-series data to create new versions which exclude any sleep time after 8AM or so). I think we can safely include:
how long it took to fall asleep;
what time I went to sleep; which gives us a smaller estimate of 15 minutes:
zeo$Start.of.Night <- sapply(strsplit(as.character(zeo$Start.of.Night), " "), function(x) { x[[2]] })
zeo$Start.of.Night <- sapply(zeo$Start.of.Night, interval)
summary(lm(formula = Rise.Time ~ Morning.Caffeine + Start.of.Night + Time.to.Z, data = zeo))
#
# Residuals:
# Min 1Q Median 3Q Max
# -137.86 -32.13 1.84 32.29 109.22
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 63.982 45.647 1.40 0.163
# Morning.CaffeineTRUE -15.847 8.321 -1.90 0.059
# Start.of.Night 0.519 0.100 5.17 7.7e-07
# Time.to.Z 0.286 0.271 1.05 0.294Finally, let’s check for damage to my sleep; it’s no good avoiding sleeping in if that then makes me feel like shit:
wilcox.test(ZQ ~ Morning.Caffeine, conf.int=TRUE, data=zeo)
#
# Wilcoxon rank sum test with continuity correction
#
# data: ZQ by Morning.Caffeine
# W = 2086, p-value = 0.7491
# alternative hypothesis: true location shift is not equal to 0
# 95% confidence interval:
# -4 3
# sample estimates:
# difference in location
# -1
wilcox.test(Morning.Feel ~ Morning.Caffeine, conf.int=TRUE, data=zeo)
#
# Wilcoxon rank sum test with continuity correction
#
# data: Morning.Feel by Morning.Caffeine
# W = 2069, p-value = 0.6568
# alternative hypothesis: true location shift is not equal to 0
# 95% confidence interval:
# -1.34e-05 1.98e-05
# sample estimates:
# difference in location
# -5.209e-05These are the 2 main measures of whether sleep quality have degraded, and both look good. So it seems the morning caffeine correlates with earlier risings but not with worse sleep or feeling bad when I get up.
Correlation!=causation; there’s a plausible alternative: on days when I feel like sleeping in, I ‘forgot’ to take a caffeine pill. So it’s worth testing. How long does the experiment need to be for 80% power and a shift of 20 minutes? (not 15m since not sure how reliable that estimate is)
## Calculate effect size, plug into power formula:
t.test(Rise.Time ~ Morning.Caffeine, data=zeo)
#
# Welch Two Sample t-test
#
# data: Rise.Time by Morning.Caffeine
# t = 2.746, df = 81.84, p-value = 0.007417
# alternative hypothesis: true difference in means is not equal to 0
# 95% confidence interval:
# 6.23 38.99
# sample estimates:
# mean in group FALSE mean in group TRUE
# 299.9 277.2
sd(zeo$Rise.Time)
# [1] 65.19
(299.9 - 277.2) / 65.19
# [1] 0.3482
power.t.test(d=0.3482, power=0.80, type="paired", alternative="one.sided")
#
# Paired t test power calculation
#
# n = 52.37
# delta = 0.3482
# sd = 1
# sig.level = 0.05
# power = 0.8
# alternative = one.sided
#
# NOTE: n is number of *pairs*, sd is std.dev. of *differences* within pairsUsing d = 0.35 as an effect size estimate, a proper blind experiment (blocking pairs of days) will take >100 days (>50 placebo pills, >50 caffeine pills).
First Morning Caffeine Experiment
I began 2014-06-29. I made the placebo pills the usual way with Bisquick, tossed together with the caffeine pills to equalize any coating; I made 120, more than I needed, because it’s always annoying to set up & make pills, and it only took 40 minutes from start to cleanup. Unfortunately, a few days into the experiment it became clear that my old caffeine pills had absorbed some ambient moisture and the tossing had not equalized the surface flavor, so the placebo pills could be easily distinguished from the caffeine pills by both flavor & texture, rendering this not a blinded & randomized experiment but just a randomized experiment. I ran out of caffeine on 2016-05-04 and terminated the experiment with n = 441.
Analysis
Data Preparation
caffeine.r <- read.csv("~/wiki/doc/zeo/2016-05-04-caffeinemorning.csv", colClasses=c("Date", "integer"))
caffeine.c <- read.csv("~/wiki/doc/zeo/2014-06-28-gwern-zeodata-caffeinecorrelation.csv")
caffeine.c$Date <- as.Date(caffeine.c$Sleep.Date, format="%m/%d/%Y")
mp <- read.csv("~/selfexperiment/mp.csv", colClasses=c("Date", "integer"))
caffeine <- merge(mp, merge(caffeine.r, subset(caffeine.c, select=c("Date", "Morning.Caffeine")), all=TRUE), all=TRUE)
## combine Morning.Caffeine.r + Morning.Caffeine while preserving the NAs:
caffeine$Caffeine <- unlist(Map(function(a,b) { if (!is.na(a) & !is.na(b)) { return(a+b); } else
{ if(is.na(a)) { return(b);} else { return(a);}}},
caffeine$Morning.Caffeine.r, caffeine$Morning.Caffeine))
zeo <- read.csv("~/wiki/doc/zeo/gwern-zeodata.csv")
zeo$Date <- as.Date(zeo$Sleep.Date, format="%m/%d/%Y")
zeo$Rise.Time <- sapply(strsplit(as.character(zeo$Rise.Time), " "), function(x) { x[2] })
interval <- function(x) { if (!is.na(x)) { if (grepl(" s",x)) as.integer(sub(" s","",x))
else { y <- unlist(strsplit(x, ":")); as.integer(y[[1]])*60 + as.integer(y[[2]]); }
}
else NA
}
zeo$Rise.Time <- sapply(zeo$Rise.Time, interval)
zeo[(zeo$Date >= as.Date("2013-03-11")),]$Rise.Time <-
(zeo[(zeo$Date >= as.Date("2013-03-11")),]$Rise.Time + 226) %% (24*60)
zeo$Start.of.Night <- sapply(strsplit(as.character(zeo$Start.of.Night), " "), function(x) { x[2] })
zeo$Start.of.Night <- sapply(zeo$Start.of.Night, interval)
zeoCaffeine <- merge(caffeine, zeo, all=TRUE)
nightSubset <- subset(zeoCaffeine[zeoCaffeine$Date>=as.Date("2013-11-10") & zeoCaffeine$Date<=as.Date("2016-08-14"),],
select=c("Date", "Start.of.Night", "Time.to.Z", "Total.Z", "Time.in.Wake", "Rise.Time", "Morning.Caffeine.r", "Morning.Caffeine", "Caffeine", "MP"))
write.csv(file="~/wiki/doc/zeo/2016-05-04-caffeine.csv", nightSubset, row.names=FALSE)Bayesian Analysis
caffeine <- read.csv("https://gwern.net/doc/zeo/2016-05-04-caffeine.csv", colClasses=c("Date", rep("numeric", 9)))
wilcox.test(Rise.Time ~ Morning.Caffeine.r, conf.int=TRUE, data=caffeine)
# Wilcoxon rank sum test with continuity correction
#
# data: Rise.Time by Morning.Caffeine.r
# W = 20672.5, p-value = 0.4470533
# alternative hypothesis: true location shift is not equal to 0
# 95 percent confidence interval:
# -5.000008791 14.999948639
# sample estimates:
# difference in location
# 4.99994868
library(ggplot2)
qplot(Date, Rise.Time, color=as.logical(Morning.Caffeine.r), data=caffeine) + theme(legend.position = "none") + stat_smooth()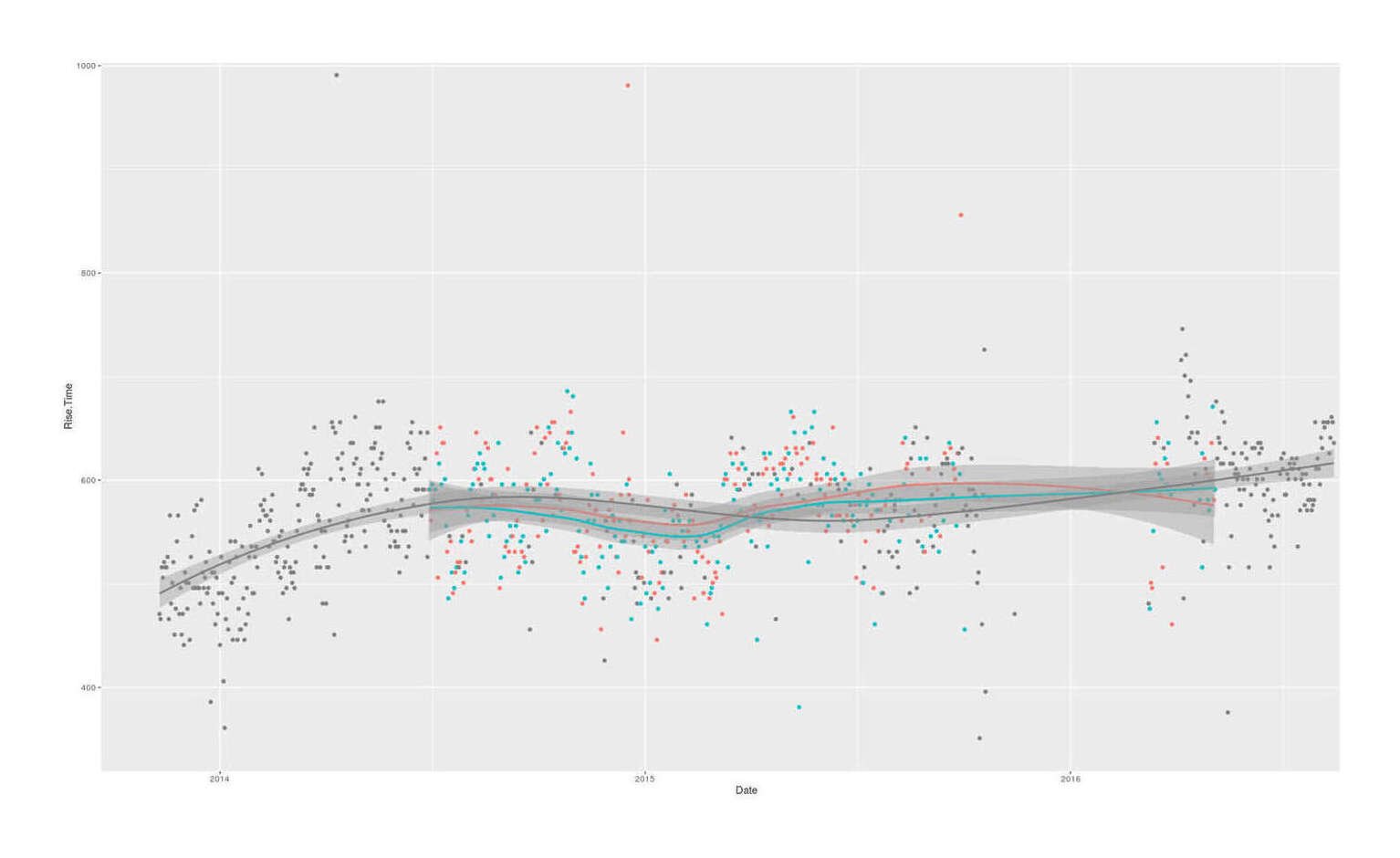
Waking up time vs randomized caffeine pill, 2014–2016
The U-test is unimpressed, but we’ll continue on with a more detailed mediation analysis, examining the impact of the two caffeine variables on Rise.Time and MP adjusting for Start.of.Night (as the only available sleep variable unaffected by the intervention). The plot of rise time shows clear temporal trends, which makes it a very good thing that randomization was done on a daily basis; we must be especially cautious about anything which might be messed up by temporal trends, such as data imputation (if I try expanding the dataset by imputing ‘0’ for all the days which did indeed not have caffeine, the results would be that using caffeine makes me wake up later, because much of the non-caffeine use is confounded with earlier rise times earlier in the dataset).
I also transform to more normality some sleep variables which are skewed, scale the dataset, and add some mildly informative priors (implying mostly that effects larger than 1SD are unlikely) to stabilize the blavaan run:
library(blavaan)
## transform
caffeine$Time.to.Z.root <- caffeine$Time.to.Z^(1/3)
caffeine$Rise.Time.root <- sqrt(caffeine$Rise.Time)
caffeine$Total.Z.2 <- caffeine$Total.Z^2
caffeine$Time.in.Wake.log <- log1p(caffeine$Time.in.Wake)
model1 <- 'Rise.Time.root ~ Start.of.Night + Time.to.Z.root + Morning.Caffeine.r + Morning.Caffeine
Total.Z.2 ~ Start.of.Night + Time.to.Z.root + Morning.Caffeine.r + Morning.Caffeine
Time.in.Wake.log ~ Start.of.Night + Time.to.Z.root + Morning.Caffeine.r + Morning.Caffeine
MP ~ Start.of.Night + Time.to.Z.root + Total.Z.2 + Time.in.Wake.log +
Morning.Caffeine.r + Morning.Caffeine + Rise.Time.root'
b <- bsem(model1, convergence="auto", burnin=300000,
dp = dpriors(nu = "dnorm(0,1)", alpha = "dnorm(0,1)", beta = "dnorm(0,200)"),
n.chains=7, jagcontrol=list(method="rjparallel"), fixed.x=FALSE,
data=scale(caffeine[,-1]))
summary(b)
# Used Total
# Number of observations 994 1016
#
# Number of missing patterns 7
#
# Statistic MargLogLik PPP
# Value -8208.015 0.000
#
# Parameter Estimates:
#
# Information MCMC
# Standard Errors MCMC
# Post.Mean Post.SD HPD.025 HPD.975 PSRF Prior
# Rise.Time.root ~
# Start.of.Night 0.230 0.039 0.152 0.306 1.039 dnorm(0,200)
# Time.to.Z.root 0.008 0.033 -0.056 0.072 1.014 dnorm(0,200)
# Morning.Cffn.r -0.041 0.052 -0.142 0.063 1.046 dnorm(0,200)
# Morning.Caffen -0.175 0.077 -0.313 -0.019 1.024 dnorm(0,200)
# Total.Z.2 ~
# Start.of.Night -0.307 0.037 -0.379 -0.235 1.015 dnorm(0,200)
# Time.to.Z.root 0.073 0.031 0.012 0.134 1.009 dnorm(0,200)
# Morning.Cffn.r -0.040 0.048 -0.134 0.055 1.028 dnorm(0,200)
# Morning.Caffen -0.121 0.097 -0.294 0.071 1.055 dnorm(0,200)
# Time.in.Wake.log ~
# Start.of.Night -0.079 0.034 -0.144 -0.01 1.002 dnorm(0,200)
# Time.to.Z.root 0.130 0.032 0.068 0.192 1.001 dnorm(0,200)
# Morning.Cffn.r 0.000 0.043 -0.086 0.083 1.003 dnorm(0,200)
# Morning.Caffen -0.030 0.061 -0.145 0.094 1.025 dnorm(0,200)
# MP ~
# Start.of.Night -0.042 0.036 -0.112 0.03 1.000 dnorm(0,200)
# Time.to.Z.root 0.069 0.033 0.005 0.132 1.000 dnorm(0,200)
# Total.Z.2 -0.068 0.035 -0.137 0 1.002 dnorm(0,200)
# Time.in.Wak.lg -0.004 0.032 -0.067 0.058 1.000 dnorm(0,200)
# Morning.Cffn.r 0.025 0.042 -0.058 0.107 1.003 dnorm(0,200)
# Morning.Caffen 0.027 0.052 -0.073 0.131 1.003 dnorm(0,200)
# Rise.Time.root -0.056 0.034 -0.123 0.012 1.001 dnorm(0,200)
#
# Covariances:
# Post.Mean Post.SD HPD.025 HPD.975 PSRF Prior
# Start.of.Night ~~
# Time.to.Z.root -0.328 0.036 -0.4 -0.26 1.002 dbeta(1,1)
# Morning.Cffn.r 0.039 0.071 -0.103 0.182 1.371 dbeta(1,1)
# Morning.Caffen -0.198 0.167 -0.519 0.128 1.200 dbeta(1,1)
# Time.to.Z.root ~~
# Morning.Cffn.r -0.054 0.053 -0.157 0.051 1.152 dbeta(1,1)
# Morning.Caffen 0.067 0.105 -0.136 0.28 1.236 dbeta(1,1)
# Morning.Caffeine.r ~~
# Morning.Caffen 0.161 0.216 -0.241 0.623 1.236 dbeta(1,1)
# ...The fairly similar estimates for Morning.Caffeine.r and Morning.Caffeine suggests that the quasi-experimental alternate-day intervention yields the same effect as the randomized one and they can be merged for a more precise estimate (since blavaan doesn’t yet support multilevel modeling):
model2 <- 'Rise.Time.root ~ Start.of.Night + Time.to.Z.root + Caffeine
Total.Z.2 ~ Start.of.Night + Time.to.Z.root + Caffeine
Time.in.Wake.log ~ Start.of.Night + Time.to.Z.root + Caffeine
MP ~ Start.of.Night + Time.to.Z.root + Total.Z.2 + Time.in.Wake.log +
Caffeine + Rise.Time.root'
b2 <- bsem(model2, convergence="auto", burnin=60000,
dp = dpriors(nu = "dnorm(0,1)", alpha = "dnorm(0,1)", beta = "dnorm(0,200)"),
n.chains=7, jagcontrol=list(method="rjparallel"), fixed.x=FALSE,
data=scale(caffeine[,-1]))
summary(b2)
# Used Total
# Number of observations 994 1016
#
# Number of missing patterns 6
#
# Statistic MargLogLik PPP
# Value -8206.054 0.000
#
# Parameter Estimates:
#
# Information MCMC
# Standard Errors MCMC
#
# Regressions:
# Post.Mean Post.SD HPD.025 HPD.975 PSRF Prior
# Rise.Time.root ~
# Start.of.Night 0.254 0.031 0.193 0.315 1.000 dnorm(0,200)
# Time.to.Z.root 0.009 0.031 -0.052 0.068 1.000 dnorm(0,200)
# Caffeine -0.013 0.037 -0.085 0.059 1.001 dnorm(0,200)
# Total.Z.2 ~
# Start.of.Night -0.290 0.030 -0.349 -0.23 1.000 dnorm(0,200)
# Time.to.Z.root 0.076 0.030 0.018 0.137 1.000 dnorm(0,200)
# Caffeine -0.043 0.037 -0.116 0.031 1.001 dnorm(0,200)
# Time.in.Wake.log ~
# Start.of.Night -0.077 0.032 -0.139 -0.014 1.000 dnorm(0,200)
# Time.to.Z.root 0.131 0.031 0.067 0.19 1.000 dnorm(0,200)
# Caffeine 0.007 0.039 -0.069 0.085 1.001 dnorm(0,200)
# MP ~
# Start.of.Night -0.047 0.035 -0.116 0.02 1.000 dnorm(0,200)
# Time.to.Z.root 0.068 0.032 0.006 0.133 1.000 dnorm(0,200)
# Total.Z.2 -0.071 0.033 -0.137 -0.006 1.000 dnorm(0,200)
# Time.in.Wak.lg -0.005 0.032 -0.069 0.057 1.000 dnorm(0,200)
# Caffeine 0.040 0.036 -0.028 0.111 1.000 dnorm(0,200)
# Rise.Time.root -0.063 0.033 -0.129 0 1.000 dnorm(0,200)
#
# Covariances:
# Post.Mean Post.SD HPD.025 HPD.975 PSRF Prior
# Start.of.Night ~~
# Time.to.Z.root -0.329 0.036 -0.4 -0.258 1.001 dbeta(1,1)
# Caffeine 0.064 0.068 -0.061 0.203 1.065 dbeta(1,1)
# Time.to.Z.root ~~
# Caffeine 0.013 0.048 -0.077 0.107 1.038 dbeta(1,1)
# ...
BF(b, b2)
# Laplace approximation to the log-Bayes factor (experimental):
# -1.962
library(lavaan)
s <- sem(model1, se="boot", missing="FIML", data=scale(caffeine[,-1]))
s2 <- sem(model2, se="boot", missing="FIML", data=scale(caffeine[,-1]))
anova(s, s2)
# Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
# s 3 16241.960 16374.307 61.42858
# s2 3 16279.827 16392.567 97.02922 35.60063 0 < 2.22e-16
summary(s)
# lavaan (0.5-20) converged normally after 25 iterations
#
# Used Total
# Number of observations 994 1016
#
# Number of missing patterns 7
#
# Estimator ML
# Minimum Function Test Statistic 61.429
# Degrees of freedom 3
# P-value (Chi-square) 0.000
#
# Parameter Estimates:
#
# Information Observed
# Standard Errors Bootstrap
# Number of requested bootstrap draws 1000
# Number of successful bootstrap draws 1000
#
# Regressions:
# Estimate Std.Err Z-value P(>|z|)
# Rise.Time.root ~
# Start.of.Night 0.267 0.045 5.992 0.000
# Time.to.Z.root 0.056 0.040 1.403 0.161
# Morning.Cffn.r -0.107 0.085 -1.261 0.207
# Morning.Caffen -0.378 0.052 -7.323 0.000
# Total.Z.2 ~
# Start.of.Night -0.395 0.079 -5.029 0.000
# Time.to.Z.root 0.095 0.047 2.005 0.045
# Morning.Cffn.r -0.087 0.079 -1.107 0.268
# Morning.Caffen -0.344 0.077 -4.439 0.000
# Time.in.Wake.log ~
# Start.of.Night -0.097 0.041 -2.374 0.018
# Time.to.Z.root 0.165 0.038 4.369 0.000
# Morning.Cffn.r -0.004 0.053 -0.075 0.940
# Morning.Caffen -0.092 0.066 -1.390 0.165
# MP ~
# Start.of.Night -0.052 0.042 -1.227 0.220
# Time.to.Z.root 0.082 0.036 2.287 0.022
# Total.Z.2 -0.079 0.047 -1.685 0.092
# Time.in.Wak.lg -0.005 0.035 -0.136 0.892
# Morning.Cffn.r 0.042 0.050 0.845 0.398
# Morning.Caffen 0.045 0.074 0.609 0.543
# Rise.Time.root -0.049 0.049 -1.005 0.315A log BF of >0 favors the second model, while <0 favors the first model; so a log BF of -1.962 or (exponentiated) a BF of 0.14 suggests that the merged caffeine variable is ~1/6th as likely as the original model and we shouldn’t use it. This agrees with the lavaan-based ANOVA and AICs/BICs which favor the original two-caffeine-variable.
Total Effect
The SEM expresses the fact that the morning caffeine can affect a variety of outcomes, which can themselves affect the most important outcome, MP. So the morning caffeine has a direct effect on the MP rating, but also has an indirect effect through sleep variables like rise time or total sleep. There’s a 78% probability that the caffeine caused an earlier rise time, but that doesn’t answer the broader question, for which we need to extract all the possible pathways and estimate a total effect.
samples <- combine.mcmc(b@external$runjags$mcmc)
## Morning.Caffeine.r is the third variable in the samples, "beta[3,1]"
posteriorSamplesRiseTimeCaffeine <- samples[,3]
mean(posteriorSamplesRiseTimeCaffeine<0)
# [1] 0.7870357143
# beta[7,1]
posteriorSamplesTotalzCaffeine <- samples[,7]
# beta[11,1]
posteriorSamplesTimeinwakeCaffeine <- samples[,11]
# beta[17,1]
posteriorSamplesMPCaffeine <- samples[,17]
# beta[19,1]
posteriorSamplesMPRiseTime <- samples[,19]
# beta[15,1]
posteriorSamplesMPTotalz <- samples[,15]
# beta[16,1]
posteriorSamplesMPTimeinwake <- samples[,16]
totalEffectMPCaffeine <- posteriorSamplesMPCaffeine + posteriorSamplesRiseTimeCaffeine*posteriorSamplesMPRiseTime +
posteriorSamplesTotalzCaffeine*posteriorSamplesMPTotalz +
posteriorSamplesMPTimeinwake*posteriorSamplesTimeinwakeCaffeine
mean(totalEffectMPCaffeine>0)
# [1] 0.76425
summary(totalEffectMPCaffeine * sd(caffeine$MP, na.rm=TRUE))
# 1. Empirical mean and standard deviation for each variable,
# plus standard error of the mean:
# Mean SD Naive SE Time-series SE
# 0.0301945943 0.0424681462 0.0002537957 0.0007091098
# 2. Quantiles for each variable:
# 2.5% 25% 50% 75% 97.5%
# -0.054155266 0.001929353 0.030434397 0.058675436 0.112366851The indirect and direct effects cumulatively imply a 76% probability that the morning caffeine use caused an increase in my MP ratings.
Decision Analysis
How much is that worth in practice? 200mg caffeine pills cost ~$0.05/pill; with a mean effect of 0.03 (1/33), if I found it worthwhile, I would implicitly value a +1 in my MP rating at $2.5.
(1 / (mean(totalEffectMPCaffeine) * sd(caffeine$MP, na.rm=TRUE))) * 0.05
# [1] 2.495673554
summary(totalEffectMPCaffeine * sd(caffeine$MP, na.rm=TRUE) * 4.8 - 0.05)
# 1. Empirical mean and standard deviation for each variable,
# plus standard error of the mean:
# Mean SD Naive SE Time-series SE
# 0.0461664235 0.1352563209 0.0008083111 0.0022584358
# 2. Quantiles for each variable:
# 2.5% 25% 50% 75% 97.5%
# -0.22247850 -0.04385523 0.04693017 0.13687474 0.30787592
(0.0461664235*365.25) / log(1.05)
# [1] 345.60831I would certainly pay $2.4/day or $75/month for a daily boost of +1; I would pay up to, I think, around $150/month ($4.8/day), suggesting that the profit would technically be profitable at ~$0.046/day (ignoring the hassle of taking a pill before waking up) or a NPV of $345. That said, I would put having to take a pill before waking up at somewhere around $0.05 so… it’s a wash. Why bother? That’s a trivial near-zero gain and it’s based on flimsy evidence with considerable possibility of net negative effects.
My opinion here is that the randomized result shows that it’s not worthwhile for me despite the highly promising initial results.
What is the value of further experimentation? EVSI for a $12 jar of 240x200mg caffeine pills:
evsis <- replicate(50, {
n_additional <- 240 # $12 jar of 200mg caffeine pills
## bootstrap collection of additional data from the randomized experiment:
newData <- caffeine[!is.na(caffeine$Morning.Caffeine.r),]
indices <- sample(1:nrow(newData), 240, replace=TRUE)
newData <- rbind(caffeine, newData[indices,])
## delete Morning.Caffeine from the model since we don't need it anymore
model3 <- 'Rise.Time.root ~ Start.of.Night + Time.to.Z.root + Morning.Caffeine.r
Total.Z.2 ~ Start.of.Night + Time.to.Z.root + Morning.Caffeine.r
Time.in.Wake.log ~ Start.of.Night + Time.to.Z.root + Morning.Caffeine.r
MP ~ Start.of.Night + Time.to.Z.root + Total.Z.2 + Time.in.Wake.log +
Morning.Caffeine.r + Rise.Time.root'
## evaluate
b_new <- bsem(model3, convergence="auto", burnin=300000, test="none",
dp = dpriors(nu = "dnorm(0,1)", alpha = "dnorm(0,1)", beta = "dnorm(0,200)"),
n.chains=7, jagcontrol=list(method="rjparallel"), fixed.x=FALSE,
data=scale(newData[,-1]))
## extract posteriors for coefficients, combine by paths, to get a net effect
samples <- combine.mcmc(b_new@external$runjags$mcmc)
posteriorSamplesRiseTimeCaffeine <- samples[,3]
posteriorSamplesTotalzCaffeine <- samples[,7]
posteriorSamplesTimeinwakeCaffeine <- samples[,11]
posteriorSamplesMPCaffeine <- samples[,17]
posteriorSamplesMPRiseTime <- samples[,19]
posteriorSamplesMPTotalz <- samples[,15]
posteriorSamplesMPTimeinwake <- samples[,16]
totalEffectMPCaffeine <- posteriorSamplesMPCaffeine + posteriorSamplesRiseTimeCaffeine*posteriorSamplesMPRiseTime +
posteriorSamplesTotalzCaffeine*posteriorSamplesMPTotalz +
posteriorSamplesMPTimeinwake*posteriorSamplesTimeinwakeCaffeine
## estimate profit
oldProfit <- 0
newProfit <- mean(totalEffectMPCaffeine * sd(caffeine$MP, na.rm=TRUE) * 4.8 - 0.10) / log(1.05)
print(newProfit)
return(max(oldProfit, newProfit)) }
)
mean(evsis) - 12
# [1] 42.35478143So I am going to have to run another self-experiment.