John Nash on cryptography
1955 letters of John Nash and the NSA on a cryptosystem and Nash’s belief that near-perfect cryptography could exploit exponential difficulties.
The following transcript was prepared from a PDF of John Nash’s correspondence with the NSA, which was declassified in 201214ya; I have attempted to reproduce the math as exactly as possible, and the language (correcting spelling errors). John Nash’s diagrams are edited screenshots from the PDF. Editorial notes, such as pages, are in brackets. All hyperlinks are my own insertion. (The ordering of sections is roughly the same as the PDF but with a more logical order.) An independent LaTeX/PDF transcript was also created by Mike Rosulek in 201214ya.
The original Nash letters are on display near the entrance of the National Cryptologic Museum located next to NSA headquarters in Fort Mead, Maryland, as of 2016-09-22; the PDF scan doesn’t give a good impression of how large Nash’s handwriting is, or how colorful the diagrams are. —Editor
Primary
Nash
To Major Grosjean
[pg2] Dear Major Grosjean,
I have written RAND concerning the machine description. This was handwritten and was sent to NSA late last spring, I believe, or sent to someone there. Essentially the same machine description was once sent to a Navy Communication Center in Washington, I think.
I have discussed the machine and general exponential conjecture with R.C. Blanchfield and A.M. Gleason who have worked for NSA. Recently a conversation with Professor Huffman here indicated that he has recently been working on a machine with similar objectives. Since he will be consulting for NSA I shall [pg3] discuss my ideas with him. He has developed minimal redundancy coding methods.
I hope my handwriting, etc. do not give the impression I am just a crank or circle-squarer. My position here is Assist. Professor of math. My best known work is in game theory (reprint, sent separately). I mention these things only in the interest of securing a most careful consideration of the machine and ideas by your most competent associates.
If the machine description does not turn up, I will provide another. Also I shall be happy to provide any additional information or answer any queries to the best of my ability.
With many thanks for your prompt reply, I am
Sincerely Yours,
John Nash
Letter Concerns Enciphering
[pg4] Dear Sirs:
An enciphering-deciphering machine (in general outline) of my invention has been sent to your organization by way of the RAND corporation. In this letter I make some remarks on a general principle relevant to enciphering in general and to my machine in particular. This principle seems quite important to me, and I have some reason to believe you may not be fully aware of it.
Consider an enciphering process with a finite “key”, operating on binary messages. Specifically, we can assume the process described by a function
Yi = F(α, α2, … αr; Xi, Xi−1, Xi−2, … Xi−n)
where the α’s, X’s, and Y’s are mod 2 and where if Xi is changed, with the other X’s and α’s left fixed then Yi is changed.
[pg5] The α’s denote the “key” containing r bits of information. n is the maximum span of the “memory” of the process. If n were ∞ the arguments given below would not be basically altered.
To consider the resistance of an enciphering process to being broken we should assume that at same times the enemy knows everything but the key being used and to break it needs only discover the key from this information.
We see immediately that in principle the enemy needs very little information to begin to break down the process. Essentially, as soon as r bits of enciphered message have been transmitted the key is about determined. This is no security, for a practical key should not be too long. But this does not consider how easy or difficult it is for the enemy to make the computation determining the key. If this computation, [pg6] although possible in principle, were sufficiently long at best then the process could still be secure in a practical sense.
The most direct computation procedure would be for the enemy to try all 2r possible keys, one by one. Obviously this is easily made impractical for the enemy by simply choosing r large enough.
In many cruder types of enciphering, particularly those which are not auto-coding, such as substitution ciphers (letter for letter, letter pair for letter pair, triple for triple…) shorter means for computing the key are feasible, essentially because the key can be determined piece meal, one substitution at a time.
So a logical way to classify enciphering processes is by the way in which the computation length for the computation of the key increases with increasing length of the key. This is at best exponential [pg7] and at worst, probably a relatively small power of r, ar2 or ar3, as in substitution ciphers.
Now my general conjecture is as follows: For almost all sufficiently complex types of enciphering, especially where the instructions given by different portions of the key interact complexly with each other in the determination of their ultimate effects on the enciphering, the mean [?] key computation length increases exponentially with the length of the key, or in other words, with the information content of the key.
The significance of this general conjecture, assuming its truth, is easy to see. It means that it is quite feasible to design ciphers that are effectively unbreakable. As ciphers become more sophisticated the game of cipher breaking by skilled teams, etc., should become a thing of the past.
[pg8] The nature of this conjecture is such that I cannot prove it, even for a special type of ciphers. Nor do I expect it to be proven. But this does not destroy its significance. The probability of the truth of the conjecture can be guessed at on the basis of experience with enciphering and deciphering.
If qualified opinions incline to believe in the exponential conjecture, then I think we (the U.S.) can not afford not to make use of it. Also we should try to keep track of the progress of foreign nations towards “unbreakable” types of ciphers.
Since the U.S. presumably does not want other nations to use ciphers we cannot expect to break, this general principle should probably be studied but kept secret.
I believe the enciphering-deciphering machine I invented and had transmitted to the N.S.A. via RAND has this “unbreakable” property. In addition it has several other advantages in that [pg9] the same physical machine would function both for ciphering and deciphering and that it is auto-synchronizing and recovers after isolated errors in transmission. These properties are not typical of enciphering systems which are auto-coding. Also it is suitable for an all electronic, ultra rapid, embodiment.
I do not expect any informative answer to this letter, yet it would be nice to have some sort of answer. I would be happy to explain more fully anything which is not clear in my letter, or to amplify on it.
I have been treating my ideas as information deserving some secrecy precautions, yet I feel it is important to communicate them to the right people. I hope the material in this letter can obtain prompt consideration by very highly competent men, versed in the field.
Sincerely.
John Nash
John Nash
Asst. Professor Math.
Machine Description
[pg12] E. M. Gibson, Lt.Col., AGC, Asst. Adj. Gen.
Dear Sir:
Here is a description of my enciphering-deciphering machine.
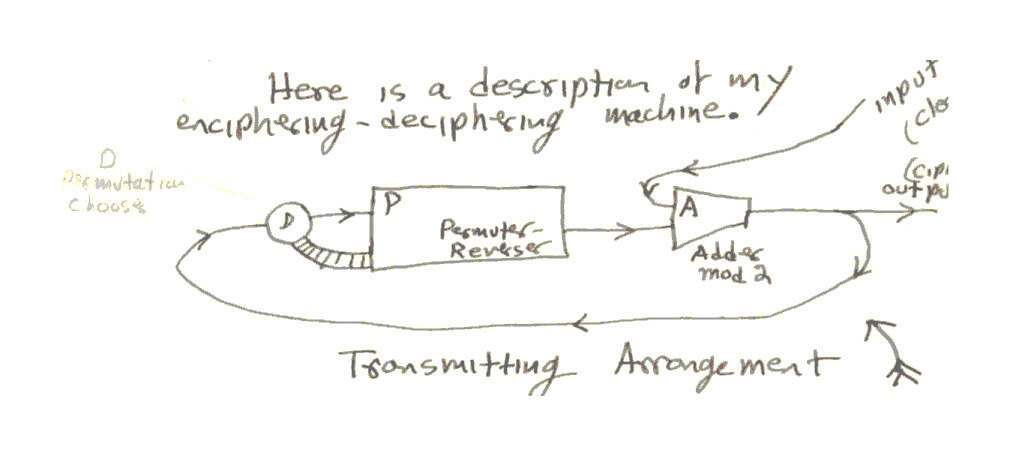
The transmitting arrangement
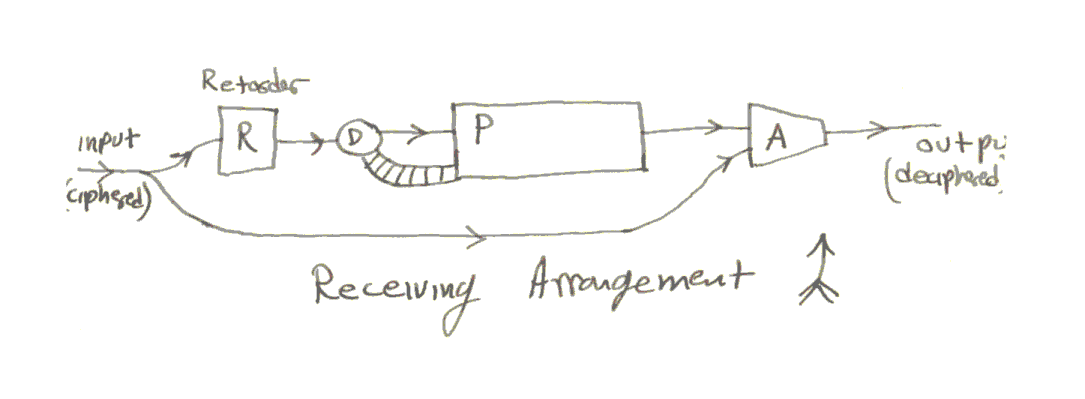
The deciphering arrangement
In the receiving arrangement the same components are used except for the addition of the retarder, which is a one-unit delay. The messages are to be sequences of binary digits (numbers mod 2). The machines work on a cycling basis, performing certain operations [pg13] during each cycle.
During each cycle the adder, A, takes in two digits and adds them and sends on the sum obtained from the previous addition. The delay in this addition necessitates the retarder, R, in the receiving circuit.
The permuter will be described in more detail below. It takes in a digit from D during each cycle and also puts out a number. What it does, which is the choice between two permutations is determined by what digit (1 or 0) is in D at the time. The permuter always has a number of digits remembered within it. Each cycle it shuffles them around, changing some 1’s to zeros, sends one digit on, and takes in a digit from D.
In operation the input of the receiver is the output of the transmitter. So the input to R is the same as the input to D in the transmitter. Hence the output of P in the receiver is the same as the out-put of P in the transmitter, except for a one-unit lag.
[pg14] So the adder A in the receiver gets: (1) the out-put of A in the transmitter, and (2) the previous input from P(trans.) to A(trans). Now since binary addition is the same as binary subtraction (ie. + & - mod 2 are the same) the output of A(receiv.) will be the previous input to A(trans.) From the input to the transmitter, ie. it will be the clear or unciphered message.
The permuter, P, and “decider”, D, work as follows, illustrated by example:
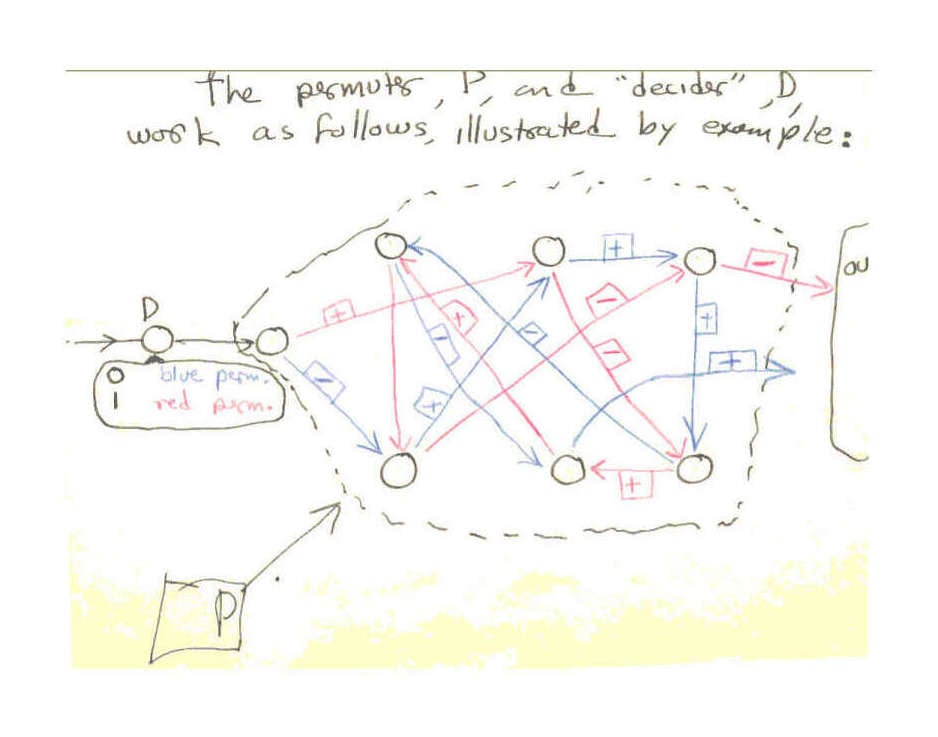
Permutation example
[pg15] The circles represent places where a digit can be stored. During each cycle either the red permutation of digits or the blue takes place. This is decided by the digit in D at the beginning of the cycle. The D digit moves to the first circle or storage place in P during the cycle after it has determined the choice of the permutation.
Both permutations should cycle through all the places in P, so that a digit would be carried through all of them and out under its action alone.
In addition to moving digits around the permutations can change 1’s to 0’s and v.v. For example
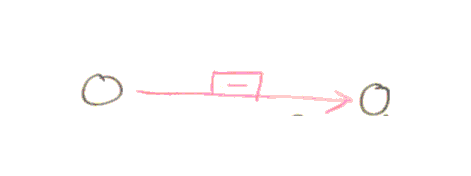
Shift digit left
represents a shift of the digit in the left circle to the right with this change

Change definition
[pg16] The “key” for the enciphering machine is the choice of the permutations. If there are n storage points in P, not counting the first one, which receives the digit from D, then there are [n!2n+1]2 possible keys.
I guess I can rely on your people to check on the possession of this machine of the various properties I claimed for it in a previous letter. I hope the correspondence I have sent in receives careful attention from the most qualified people, because I think the basic points involved are very important.
Sincerely,
John Nash
Assist. Professor Math.
P.S. Various devices could be added to the machine, but I think it would generally be better to enlarge the permuter than to add anything. Of course error-correcting coding could occasionally be a useful adjunct.
NSA
To Nash (1)
[pg10] Serial: 531
25 Jan 1955
Mr. John Nash
Department of Mathematics
Massachusetts Institute of Technology
Cambridge 39, Massachusetts
Dear Mr. Nash:
Your recent letter, received 18 January 195571ya, is noted. Technicians at this Agency recall a very interesting discussion with you which took place approximately four years ago, and will welcome the opportunity to examine your ideas on the subject of cryptography.
A check within this Agency has, unfortunately, disclosed no information on your machine. A description of the principles involved will be appreciated.
Sincerely,
E. M. Gibson
Lt. Col., AGC
Assistant Adj. Gen.
cc: AG
C/S
COMSEC (3)
412
M/R: In Jan 195571ya, Mr. Nash offered general remarks on cryptography and requested evaluation of descriptive material which he had forwarded through Rand Corp. NSA Ser 236, 12 Jan 55 informed Mr. Nash that the material had not arrived. Mr. Nash in letter rec’d 18 Jan 55 states the material was sent to NSA and to a Navy Communication Center in Wash. late last spring. A check of Agency records and discussions with various individuals (R/D mathematicians and persons who might have had contact with Rand Corp.) within the Agency has uncovered nothing concerning the system. This correspondence requests a description of the machine.
In 195076ya Mr. Nash submitted material, in interview, which was evaluated by NSA as not suitable.
[signature]
M. A. Lyons, 4128, 60372, in
K C/See 2-2 [?]
To Nash (2)
[pg11] Serial: 236
12 Jan 1955
Mr. John Nash
Department of Mathematics
Massachusetts Institute of Technology
Cambridge 39, Massachusetts
Dear Mr. Nash:
Reference is made to your recent letter concerning enciphering processes. The information regarding the general principles has been noted with interest. It will be considered fully, and particularly in connection with your enciphering-deciphering machine.
The description of your machine has not yet been received from the Rand Corporation. As soon as details are received, the machine will be studied to determine whether it is of interest to the Government.
The presentation for appraisal of your ideas for safeguarding communications security is very much appreciated.
Sincerely,
D. M. Grosjean
Major WAC
Actg. Asst. Adjutant General
cc: AG
C/S
COMSEC (3)
412
M/R: Mr. Nash offers remarks on a general principle relevant to enciphering in general and to his machine in particular. The machine, which he is sending via the Rand Corporation, has not yet been received.
This letter informs Mr. Nash that his remarks are being noted and that the machine will be studied as soon as details are received. This reply coordinated with Mr. M. M. Mathews, NSA-31. This is an interim reply.
[signature]
M. A. Lyons, 4128, 30372, in
C/SEC 202
To Nash (3)
[pg17] Serial: 1358
3 Mar 1955
Mr. John Nash
Department of Mathematics
Massachusetts Institute of Technology
Cambridge 39, Massachusetts
Dear Mr. Nash:
Reference is made to your letter received in this Agency on 17 February 195571ya.
The system which you describe has been very carefully examined for possible application to military and other government use. It has been found that the cryptographic principles involved in your system, although ingenious, do not meet the necessary security requirements for official application.
Unfortunately it is impossible to discuss any details in this letter. Perhaps in the future another opportunity will arise for discussion of your ideas on the subject of cryptography.
Although your system cannot be adopted, its presentation for appraisal and your generosity in offering it for official use are very much appreciated.
It is regretted that a more favorable reply cannot be given.
Sincerely,
E. M. Gibson
Lt. Col., AGC
Assistant Adj. Gen.
cc: AG
C/S
COMSEC (3)
412
(M/R attached)
Internal
[pg18] M/R: In Jan 55 Mr. Nash offered general remarks on cryptography and requested valuation of descriptive material which he had forwarded through Rand Corp. The Material was not received from Rand Corp. Dr. Campaigne received a letter from Mr. Nash enclosing a copy of the letter (5 Apr 54) from Rand which transmitted this material to NSA. This material was found in R/D files. In the meantime Mr. Nash sent a handwritten description of his enciphering-deciphering machine.
Mr. Nash proposes a permuting cipher-text auto-key principle which has many of the desirable features of a good auto-key system; but it affords only limited security, and requires a comparatively large amount of equipment. The principle would not be used alone in its present form and suitable modification or extension is considered unlikely, unless it could be used in conjunction with other good auto-key principles.
This correspondence informs Mr. Nash that his system does not meet necessary security requirements; and expresses pleasure at the thought of an opportunity to discuss Mr. Nash’s ideas on cryptography again. Such a discussion took place in 195076ya when Mr. Nash submitted material, in interview, which was evaluated by NSA as unsuitable.
An interesting pamphlet on Non-Cooperative Games1, written by Mr. Nash was also sent to this Agency by the author for our information.
Dr. Campaigne has been informed that the reply has been written and is not interested in further coordination.
[signature]
M.A. Lyons, 4128/60372/rwb
Secondary
“National Cryptologic Museum Opens New Exhibit on Dr. John Nash”, NSA:
When people hear the name “John Nash”, many recall the movie A Beautiful Mind, in which actor Russell Crowe portrays the mathematical genius whose game-theory research as a graduate student at Princeton University earned him the Nobel Memorial Prize in Economic Sciences in 199432ya.
The National Cryptologic Museum’s newest exhibit, “An Inquisitive Mind: John Nash Letters,” features copies of correspondence between Dr. Nash and the National Security Agency (NSA) from the 1950s when he was developing his ideas on an encryption-decryption machine.
At the height of his career in mathematics, Dr. Nash wrote a series of letters to NSA, proposing ideas for such a machine. While the agency acknowledged his ideas, they were never adopted. The letters were preserved with NSA’s analysis in a collection of unsolicited correspondence received in 195571ya.
Cryptographer Ron Rivest implemented Nash’s cryptosystem in Python and assigned an examination to his class in 201214ya:
Problem 1-2. Cryptosystem proposal by Nash
In the 1950s the mathematician John Nash (now famous for his work on game theory, and also the subject the movie A Beautiful Mind), privately proposed to the National Security Agency (NSA) an idea for a cryptosystem. This proposal was just declassified (two weeks ago!); a copy of it is available on the class website as Handout # 3, together with some relevant correspondence with the NSA. Note that this proposal was not accepted by the NSA, who said that it didn’t meet their security requirements.
What reasons, if any, can you figure out for this rejection? (Note that this assignment is a bit of an open problem! Do the best you can, and write up what you can figure out. We don’t know the answer to this question ourselves…)
“A Brief History of NP-Completeness, 1954–58201214ya”, David S. 2012:
The other famous mathematician whose letters foreshadowed the theory of NP-completeness was John Nash, Nobel Prize winner for Economics and subject of both the book and the movie A Beautiful Mind. In 195571ya, Nash sent several handwritten letters about encryption to the United States National Security Agency, which were not declassified and made publicly available until 201214ya [1]. In them, he observes that for typical key-based encryption processes, if the plain texts and encrypted versions of some small number of messages are given, then the key is determined. This is not technically correct, since in addition there must be sufficient entropy in the plain texts, but Nash’s arguments apply as well to the problem of finding some key consistent with the encryptions. His central observation was that even if the key is determined, it still may not be easy to find.
If the key is a binary string of length r, exhaustive search will work (as it did for Gödel), but takes time exponential in r. For weak cryptosystems, such as substitution ciphers, there are faster techniques, taking time 𝒪(r2) or 𝒪(r3), but Nash conjectured that “for almost all sufficiently complex types of enciphering”, running time exponential in the key length is unavoidable.
This conjecture would imply that P ≠ NP, since the decryption problem he mentions is polynomial-time equivalent to a problem in NP: Given the data on plain and encrypted texts and a prefix x of a key, is there a key consistent with the encryptions which has x as a prefix? It is a stronger conjecture, however, since it would also rule out the possibility that all problems in NP can, for instance, be solved in time n𝒪(logn), which, although non-polynomial, is also not what one typically means by “exponential”. Nash is also making a subsidiary claim that is in essence about the NP-hardness of a whole collection of decryption problems. This latter claim appears to be false. Nash proposed an encryption scheme of the type he specified, but the NSA observed in private notes that it provided only limited security, and since the publication of the letters modern researchers have found it easy to break [2]. Also, like Gödel, Nash did not make the leap from low-order polynomial time to polynomial time in general. He did however, correctly foresee the mathematical difficulty of the P versus NP problem. He admitted that he could not prove his conjecture, nor did he expect it to be proved, even if it were true.
Shiro Kawai implemented Nash’s system in Scheme.
Bloggers on the significance of the letter:
-
In it, John Nash makes the distinction between polynomial time and exponential time, conjectures that there are problems that cannot be solved faster than in exponential time, and uses this conjecture as the basis on which the security of a cryptosystem (of his own design) relies. He also anticipates that proving complexity lower bounds is a difficult mathematical problem…These letters predate even Gödel’s [195670ya] letter to Von Neumann, which goes into much less detail about complexity, and yet has also been taken to anticipate complexity theory and the P versus NP problem.
-
He then goes on to put forward an amazingly prescient analysis anticipating computational complexity theory as well as modern cryptography. In the letter, Nash takes a step beyond Shannon’s information-theoretic formalization of cryptography (without mentioning it) and proposes that security of encryption be based on computational hardness—this is exactly the transformation to modern cryptography made two decades later by the rest of the world (at least publicly…). He then goes on to explicitly focus on the distinction between polynomial time and exponential time computation, a crucial distinction which is the basis of computational complexity theory, but made only about a decade later by the rest of the world…He is very well aware of the importance of this “conjecture” and that it implies an end to the game played between code-designers and code-breakers throughout history. Indeed, this is exactly the point of view of modern cryptography…Surprisingly, for a mathematician, he does not even expect it to be solved. Even more surprisingly he seems quite comfortable designing his encryption system based on this unproven conjecture. This is quite eerily what modern cryptography does to this day: conjecture that some problem is computationally hard; not expect anyone to prove it; and yet base their cryptography on this unproven assumption.
-
Some caution is needed here…it seems clear to me that Nash did foresee important ideas of modern cryptography. This is great and deserves recognition. However, it seems also very clear that he did not foresee (in fact: could not even imagine) modern complexity theory. Why else would he say that he does not think that the exponential hardness of the problem could ever be proven? It is true that the computational hardness of key tasks in modern cryptography is an unsolved problem, but we have powerful tools to prove hardness results in many other cases. So if Nash had anticipated complexity theory as such, then his remark would mean that he would also have foreseen these difficulties…Overall, it seems clear that a prediction of complexity theory or its current incapacity with respect to cryptographic problems cannot be found in this text, which does by no means diminish the originality of the remarks on cryptography. One could also grant him a certain mathematical intuition that some computational problems could be inherently hard to solve, although I don’t see any hint that he believes that such hardness could ever become a precise mathematical property.
Geoffrey Watson agrees:
This is very interesting as a historical document, but not sure that it supports the interpretations being put on it…a reasonable historical conclusion is that these ideas were just going around in the usual way. The “conjecture” is a pretty muddled bit of thinking. It presumably means that Nash thinks that there are such exponentially hard ciphers, but to convert “almost all sufficiently complex types of enciphering, especially where the instructions given by different portions of the key interact complexly with each other in the determination of their ultimate effects on the enciphering” into a prescient anticipation of complexity theory is a big ask.
Philonus Atio comments that (as one might expect for early work):
I broke it in about 1 hour and I’m no expert in cryptanalysis. It is weak.
Animats suggests why the NSA may’ve rejected the system:
What Nash seems to be describing is a linear feedback shift register. This has potential as a cryptosystem, but isn’t a very good one. As the NSA pointed out, it “affords only limited security”. When Nash wrote this, Friedman had already developed the theory that allowed general cryptanalysis of rotor-type machines. But that was still highly classified. Friedman, of course, was responsible for breaking the Japanese “Purple” cipher, plus many others. Before Friedman, cryptanalysis was about guessing. After Friedman, it was about number crunching.
Friedman was the head cryptanalyst at NSA at the time. Within NSA, it would have been known that a linear feedback shift register was a weak key generator. So this idea was, properly, rejected. At least NSA looked at it. Friedman’s hard line on that subject was “No new encryption system is worth looking at unless it comes from someone who has already broken a very hard one.”
The fact that a problem is NP-hard isn’t enough to make it a good key generator. The Merkle-Hellman knapsack cryptosystem, the first public-key cryptosystem published, is based on an NP-hard problem. But, like many NP-hard problems, it’s only NP-hard in the worst case. The average case is only P-hard. (Linear programming problems, and problems which can be converted to a linear programming problem, are like that.) So that public-key system was cracked. We still don’t have cryptosystems which are provably NP-hard for all cases. Factoring and elliptic curves are as good as it gets, and there’s still the possibility that a breakthrough could make factoring easy.
-
Non-cooperative games are the best-known areas of game theory, including such games as the prisoner’s dilemma and where Nash did almost all of his game theory work; results on cooperative game theories appeared later, are more complex & harder, and accordingly are much more obscure.↩︎