Skip to main content

Self-Blinded Mineral Water Taste Test

, , ,

Blind randomized taste-test of mineral/distilled/tap waters using Bayesian best-arm finding; no large differences in preference.

2017-02-15–4y2021-05-04 finished certainty: highly likely importance: 2 backlinks similar bibliography

The kind of water used in tea is claimed to make a difference in the flavor: mineral water being better than tap water or distilled water. However, mineral water is vastly more expensive than tap water.

To test the claim, I run a preliminary test of pure water to see if any water differences are detectable at all. Compared my tap water, 3 distilled water brands (Great Value, Nestle Pure Life, & Poland Spring), 1 osmosis-purified brand (Aquafina), and 3 non-carbonated mineral water brands (Evian, Voss, & Fiji) in a series of n = 67 blinded randomized comparisons of water flavor. The comparisons are modeled using a Bradley-Terry competitive model implemented in Stan; comparisons were chosen using an adaptive Bayesian best-arm sequential trial (racing) method designed to locate the best-tasting water in the minimum number of samples by preferentially comparing the best-known arm to potentially superior arms. Blinding & randomization are achieved by using a Lazy Susan to physically randomize two identical (but marked in a hidden spot) cups of water.

The final posterior distribution indicates that some differences between waters are likely to exist but are small & imprecisely estimated and of little practical concern.

Tap water taste reportedly differs a lot between cities/states. This is plausible since tea tastes so much worse when microwaved, which is speculated to be due to the oxygenation, so why not the mineral/chlorine content as well? (People often complain about tap water and buy water filters to improve the flavor, and sometimes run blinded experiments testing water filters vs tap; Capehart & Berg2018 find in a blind taste test of bottled “fine water”, subjects were slightly better than chance at guessing, preferred tap or cheap water as often, and were unable to match fine waters to advertising, while Food52’s 2 testers of 17 blind sparkling waters had difficult distinguishing types & noticed no advantage to more expensive ones.1)

Testing tea itself, rather than plain water, is tricky for a few reasons:

  • hot tea is harder to taste differences in

  • the tea flavor will tend to overpower & hide any effects from the water

  • each batch of tea will be slightly different (even if carefully weighed out, temperature checked with a thermometer, and steeped with a timer)

  • boiling different waters simultaneously requires two separate kettles (and for blinding/randomization, raises safety issues)

  • requires substantial amounts of a single or a few teas to run (since leaves can’t be reused)

  • and the results will either be redundant with testing plain water (if simple additive effects like ‘bad-tasting water makes all teas taste equally worse’) or will add in additional variance to estimate interaction effects which probably do not exist2 or are small but will use up more data (in psychology and related fields, the main effects tend to be much more common than interaction effects, which also require much larger data samples).

So a tea test is logistically more complicated and highly unlikely to deliver any meaningful inferences with feasible sample sizes as compared to a water test. On the other hand, a water test, if it indicated large differences existed, might not be relevant since those differences might still be hidden by tea or turn out to be interactions with tea-specific effects. This suggests a two-step process: first see if there are any differences in plain water; if there aren’t, there is no need to test tea, but if there is, proceed to a tea test.

This question hearkens back to R. A. Fisher’s famous “lady tasting tea” experiment and turns out to provide a bit of a challenge to my usual blinding & methods, motivating a look into Bayesian “best-arm identification” algorithms.

Waters

Well water & distilled water already on hand, so I need good commercial spring water (half a gallon or less each). I obtained 8 kinds of water:

  • tap water (I ran the tap for several minutes and then stored 3.78l in an empty distilled water container, and stored at room temperature with the others)

  • Walmart:

    • Great Value distilled water

    • Nestle Pure Life

    • Aquafina

    • Vos

    • Evian

    • Fiji Natural Water

  • Amazon:

Price, type, pH, and contents:

Water brand

Water kind

Country

Price ($/l)

Price ($)

Volume (L)

pH

Total mg/l

Calcium

Sodium

Potassium

Fluoride

Magnesium

Nitrate

Chloride

Copper

Sulfate

Arsenic

Lead

Bicarbonates

Silica

tap water

well

USA

0

0

3.78

Great Value

distilled

USA

0.23

0.88

3.78

Nestle Pure Life

distilled

USA

0.26

0.98

3.79

6.95

36

7.6

6.8

1

0.1

3.6

0.4

13.45

0.05

13.5

0.002

0.005

Voss Still Water

mineral

Norway

3.43

2.74

0.8

5.5

44

5

6

1

0.1

1

0.4

12

0.05

5

0.002

0.005

Evian

mineral

France

1.78

1.78

1

7.2

309

80

1

26

6.8

12.6

36

15

Fiji Natural Water

mineral

Fiji

1.88

1.88

1

7.7

222

18

18

4.9

0.28

15

0.27

9

0.05

1.3

0.002

0.005

152

93

Aquafina

osmosis

USA

1

1

1

5

5

4

10

250

1

250

0.010

0.005

Poland Spring

distilled

USA

3.15

9.45

3

7.2

61

7.5

5.9

0.6

0.115

1.145

0.6

10.05

0.05

3

0.0014

0.005

Notes:

  • the pH & mineral content of my tap water is unknown; it is well water untreated with chlorine or fluoride, described as very soft

  • the Great Value/Walmart distilled water doesn’t report any data on the label and there don’t seem to be any datasheets online (the pH of distilled water can apparently vary widely from the nominal value of 7 and cannot be assumed to be 7, but should the mineral contents should all at least be close to 0)

  • the Nestle Pure Life numbers are not reported on the packaging but in the current online datasheet (pg4, “2015 Water Analysis Report”); I have taken the mean when a range is reported, and the upper bound when that is reported (specifically, “ND”3)

  • Voss Still reports some numbers on the bottle, but more details are reported in an undated (metadata indicates 201113ya) report on the Voss website; for “ND” I reuse the upper bound from Nestle Pure Life

  • the Evian label reports a total of “dissolved solids at 180C: 309ppm (mg/l)”.

  • Fiji Water provides a 2014 datasheet which is more detailed than the label; “ND” as before

  • Aquafina labels provide no information beyond using reverse osmosis; they provide a 2015 datasheet, which omits pH and several other minerals; various online tests suggest Aquafina samples have pHs of 4-6, so I class it as 5

  • Poland Spring 2016 datasheet; note that the price may be inflated considerably because I had to order it online instead of buying in person from a normal retailer; like Nestle Pure Life, ranges are reported and “ND” taken as ceiling

Reporting of the mineral contents of waters is inconsistent & patchy enough that they’re unlikely to be helpful in predicting flavor ratings (while Gallagher & Dietrich2010/Dietrich & Gallagher2013 finds testers can taste mineral content, Gallagher & Dietrich 201014ya reports no particular preference, and Capehart2015 finds no consistent relationship with fine-water prices other than both very low & very high mineral contents predicts higher prices).

Design

In rating very subtle difference in flavor, the usual method is binary forced-choice comparisons, as they cannot be rated on their own (they just taste like water). So the measured data would be the result of a comparison, better/worse or win/loss. Fisher’s original “lady tasting tea” experiment used permutation tests, but he was only considering two cases & was testing the null hypothesis, while I have 8 waters where I am reasonably sure the null hypothesis of no difference in taste is indeed false and I am more interested in how large the differences are & which is best, so the various kinds of permutation or chi-squared tests in general do not work. The analogy to sporting competitions suggests that the paradigm here should be the Bradley-Terry model which is much like chess’s Elo rating system in that it models each competitor (water) as having a performance variable (flavor) on a latent scale, where the difference between one competitor’s rating and another translates into the probability it will win a comparison. (For more detailed discussion of the Bradley-Terry model, see references in Resorter.) To account for ties, the logistic distribution is expanded into an ordered logistic distribution with cutpoints to determine whether the outcome falls into 1 of 3 ranges (win/tie/loss).

With 8 waters to be ranked hierarchically using uninformative binary comparisons (which are possibly quite noisy) and sampling being costly (to my patience), it would be nice to have an adaptive experiment design which will be more sample-efficient than the simplest experiment design of simply doing a full factorial with 2 of each possible comparison (there are 28 = 28 possible pairs, since order doesn’t matter, so 2 samples each would give n = 56). In particular, I am interested less in estimating as accurately as possible all the waters (for which the optimal design minimizing total variance probably would be some sort of full factorial experiment) than I am in finding out which, if any, of the waters tastes best—which is not the multi-armed bandit setting (to which the answer would be Thompson sampling) but the closely connected “best-arm identification” problem (as well as, confusingly, the “dueling multi-armed bandit” and “preference learning”/“preference ranking” areas; I didn’t find a good overview of them all comparing & contrasting, so I’m unsure what would be the state-of-the-art for my exact problem or whose wheel I am reinventing).

Best Arm Racing Algorithms

Best arm identification algorithms are often called ‘racing’ algorithms because they sample by ‘racing’ the two best comparisons against each other, focusing their sampling on only the arms likely to be best, and periodically killing the worst ranked arms (in “successive rejects”). So they differ from Thompson sampling in that Thompson sampling, in order to receive as many rewards as possible, will tend to over-focus on the best arm while not sampling the second-best enough. Mellor20144 introduces a Bayesian best arm identification algorithm, “Ordered-Statistic Thompson Sampling”, which selects the arm to sample each round by:

  1. fitting the Bayesian model and returning the posterior distribution of estimates for each arm

  2. taking the mean of each distribution, ranking them, and finding the best arm’s mean5

  3. for the other arms, sampling 1 sample from their posteriors (similar to Thompson sampling); add a bonus constant to tune the ‘aggressiveness’ and sample more or less heavily from lower-ranked arms

  4. select the action: if any of the arm samples are greater than the best arm mean, sample from that arm, otherwise, sample again from the best arm

  5. repeat indefinitely until the experiment halts (indefinite horizon)

This works because it frequently samples from any arm which threatens to surpass the current best arm in proportion to their chance of success, otherwise it concentrates on making more precise the best arm. The usual best arm identification algorithms are for the binomial or normal distribution problems, but here we don’t have 21 ‘arms’ of pairs of waters, because it’s not the pairs we care about but the waters themselves. My suggestion is that to adapt Mellor2014’s algorithm to the Bradley-Terry competitive setting, one instead samples from each water, set the first water to be the highest mean water and then sample from the posteriors of the other waters and compare the best arm to the highest posterior sample. This is simple to implement, and like the regular best arm identification algorithm, focuses on alternatives in proportion to their probability of being superior to the current estimated best arm. (Who knows if this is optimal.)

Dynamic Programming

One alternative to my variant on ordered-statistic Thompson sampling would be to set a fixed number of samples I am willing to take (eg. n = 30) and define a reward of 1 for picking the true best water and 0 for picking any other water—thereby turning the experiment into a finite-horizon Markov decision process whose decision tree can be solved exactly by dynamic programming/backwards induction, yielding a policy for which waters to compare to maximize the probability of selecting the right one at the end of the experiment. This runs into the curse of dimensionality: with 28 possible comparisons with 2 possible outcomes, each round has 56 possible results, so over 67 samples, there are 5667 possible sequences.

Blinding

With such subtle differences, subjective expectations become a serious issue and blinding would be good to have, which also requires randomization. My usual methods of blinding & randomization, using containers of pills, do not work with water. It would be possible to do the equivalent by using water bottles shaken in a large container but inconvenient and perhaps messy. A cleaner (literally) way would be to use identical cups, one marked on the bottom to keep track of which is which after rating the waters—but how to randomize them? You can’t juggle or shake or mix up cups of water.

It occurred to me that one could use a spinning table—a Lazy Susan—to randomize pairs of cups. And then blinding is trivial, because you can easily spin a Lazy Susan without looking at it, and it will coast after spinning so you cannot subconsciously count revolutions to guesstimate which cup winds up closest to you.

Implementation

Modified version of Ken Butler’s btstan Stan code for Bradley-Terry models and my own implementation of best arm sampling for the Bradley-Terry model:

## list of unique competitors for conversion into numeric IDs:
competitors <- function(df) { unique(sort(c(df$Type1, df$Type2))) }
fitBT <- function(df) {
    types <- competitors(df)
    team1 = match(df$Type1, types)
    team2 = match(df$Type2, types)
    y = df$Win
    N = nrow(df)
    J = length(types)
    data = list(y = y, N = N, J = J, x = cbind(team1, team2))

    m <- "data {
      int<lower=0> N; // number of games
      int<lower=1> J; // number of teams
      int<lower=1,upper=3> y[N]; // results
      int x[N,2]; // indices of teams playing
    }
    parameters {
      vector[J] beta;
      real<lower=0> cc;
    }
    model {
      real nu;
      int y1;
      int y2;
      vector[2] d;

      beta ~ normal(0,5);
      cc ~ normal(0,1);

      for (i in 1:N) {
        y1 = x[i,1];
        y2 = x[i,2];
        nu = beta[y1] - beta[y2];
        d[1] = -cc;
        d[2] =  cc;
        y[i] ~ ordered_logistic(nu,d);
    } }"
    library(rstan)
    model <- stan(model_code=m, chains=1, data=data, verbose=FALSE, iter=30000)
    return(model)
    }

sampleBestArm <- function(model, df) {
    types <-  competitors(df)
    posteriorSampleMeans <- get_posterior_mean(model, pars="beta")
    bestEstimatedArm      <- max(posteriorSampleMeans[,1])
    bestEstimatedArmIndex <- which.max(posteriorSampleMeans[,1])
    ## pick one row/set of posterior samples at random:
    posteriorSamples <- extract(model)$beta[sample.int(nrow(extract(model)$beta), size=1),]
    ## ensure that the best estimated arm is not drawn, as this is pairwise:
    posteriorSamples[bestEstimatedArmIndex] <- -Inf
    bestSampledArm <- max(posteriorSamples)
    bestSampledArmIndex <- which.max(posteriorSamples)
    return(c(types[bestEstimatedArmIndex], types[bestSampledArmIndex]))
    }

plotBT <- function(df, fit, labels) {
    library(reshape2)
    posteriors <- as.data.frame(extract(fit)$beta)
    colnames(posteriors) <- labels
    posteriors <- melt(posteriors)
    colnames(posteriors) <- c("Water", "Rating")
    return(ggplot(posteriors, aes(x=Rating, fill=Water)) +
        ggtitle(paste0("n=",as.character(nrow(df)),"; last comparison: ", tail(df$Type1,n=1),
                                                                  " vs ", tail(df$Type2,n=1))) +
        geom_density(alpha=0.3) +
        coord_cartesian(ylim = c(0,0.23), xlim=c(-12,12), expand=FALSE)) }

It would be better to enhance the btstan code to fit a hierarchical model with shrinkage since the different waters will surely be similar, but I wasn’t familiar enough with Stan modeling to do so.

Experiment

To run the experiment, I stored all 8 kinds of water in the same place at room temperature for several weeks. Before running, I refrained from food or drink for 5 hours and brushed/flossed/water-picked my teeth.

For blinding, I took my two identical white Corelle stoneware mugs, and put a tiny piece of red electrical tape on the bottom of one. For randomization, I borrowed a Lazy Susan table.

The experimental procedure was:

  1. empty out both mugs and the measuring cup into a tub sitting nearby

  2. select two kinds of water according to the best arm Bayesian algorithm (calling fitBT & sampleBestArm on an updated data-frame)

  3. measure a quarter cup of the first kind of water into the marked mug and a quarter cup into the second

  4. place them symmetrically on the Lazy Susan with handles inward and touching

  5. closing my eyes, rotate the Lazy Susan at a moderate speed (to avoid tipping over the mugs) for a count of at least 30

  6. eyes still closed for good measure, grab the mug on left and take 2 sips

  7. grab the mug on the right, take 2 sips

  8. alternate sips as necessary until I decide which one is slightly better tasting

  9. after deciding, look at the bottom of the mug chosen

  10. record the winner of the comparison, and run the Bayesian model and best arm algorithm again.

Following this procedure, I made n = 67 pairwise comparisons of water:

water <- read.csv(stdin(), header=TRUE, colClasses=c("character", "character", "integer"))
"Type1","Type2","Win"
"tap water","Voss",3
"Voss","Great Value distilled",3
"Great Value distilled","Poland Spring",1
"Poland Spring","Nestle Pure Life",3
"Nestle Pure Life","Fiji",1
"Fiji","Aquafina",3
"Aquafina","Evian",3
"Evian","tap water",1
"Great Value distilled","Poland Spring",1
"Great Value distilled","tap water",1
"Great Value distilled","Nestle Pure Life",1
"Fiji","Poland Spring",3
"Fiji","Poland Spring",1
"tap water","Poland Spring",1
"Poland Spring","Fiji",3
"Poland Spring","Fiji",3
"Poland Spring","Fiji",3
"Poland Spring","Fiji",1
"Poland Spring","Fiji",3
"Poland Spring","Fiji",1
"Poland Spring","Fiji",3
"Poland Spring","Fiji",1
"Poland Spring","Aquafina",1
"Poland Spring","Fiji",3
"Poland Spring","Aquafina",1
"Aquafina","Fiji",1
"Poland Spring","Aquafina",1
"Aquafina","Fiji",1
"Fiji","Aquafina",3
"Fiji","Poland Spring",3
"Fiji","Aquafina",3
"Fiji","Poland Spring",3
"Fiji","Poland Spring",3
"Fiji","Aquafina",3
"Fiji","tap water",1
"Fiji","Aquafina",3
"Fiji","Poland Spring",1
"tap water","Aquafina",1
"Fiji","Poland Spring",1
"Fiji","Poland Spring",3
"Fiji","Poland Spring",3
"Great Value distilled","Evian",3
"Evian","Voss",1
"Voss","Nestle Pure Life",3
"Nestle Pure Life","tap water",3
"tap water","Aquafina",1
"Aquafina","Poland Spring",3
"Evian","Great Value distilled",1
"Great Value distilled","Nestle Pure Life",3
"Nestle Pure Life","Voss",3
"Voss","tap water",3
"tap water","Aquafina",1
"Aquafina","Poland Spring",1
"Aquafina","Poland Spring",3
"Evian","Great Value distilled",1
"Great Value distilled","Nestle Pure Life",3
"Nestle Pure Life","tap water",3
"tap water","Voss",3
"Voss","Aquafina",1
"Evian","Great Value distilled",3
"Great Value distilled","Nestle Pure Life",3
"Nestle Pure Life","tap water",3
"tap water","Aquafina",3
"Evian","Great Value distilled",1
"Great Value distilled","Nestle Pure Life",3
"Nestle Pure Life","tap water",3
"tap water","Aquafina",1

Analysis

types <- competitors(water); types
# [1] "Aquafina"      "Evian"     "Fiji" "Great Value distilled" "Nestle Pure Life"
# [6] "Poland Spring" "tap water" "Voss"
fit <- fitBT(water); print(fit)
# 8 chains, each with iter=30000; warmup=15000; thin=1;
# post-warmup draws per chain=15000, total post-warmup draws=120000.
#
#           mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
# beta[1]   1.18    0.01 1.89  -2.52  -0.09   1.18   2.46   4.89 23182    1
# beta[2]  -2.69    0.01 2.11  -6.95  -4.08  -2.66  -1.25   1.33 27828    1
# beta[3]   1.83    0.01 1.89  -1.89   0.55   1.83   3.10   5.56 23147    1
# beta[4]  -0.48    0.01 1.90  -4.21  -1.76  -0.48   0.81   3.21 23901    1
# beta[5]  -0.40    0.01 1.88  -4.11  -1.66  -0.40   0.88   3.27 23487    1
# beta[6]   1.42    0.01 1.89  -2.29   0.15   1.42   2.70   5.14 23173    1
# beta[7]  -0.49    0.01 1.87  -4.17  -1.74  -0.49   0.78   3.17 23084    1
# beta[8]  -0.48    0.01 1.93  -4.29  -1.78  -0.48   0.82   3.29 24494    1
# cc        0.03    0.00 0.03   0.00   0.01   0.02   0.05   0.13 83065    1
# lp__    -49.58    0.01 2.27 -54.90 -50.87 -49.24 -47.91 -46.19 40257    1
## example next-arm selection at the end of the experiment:
sampleBestArm(fit, water)
# [1] "Fiji"          "Poland Spring"

posteriorSamples <- extract(fit, pars="beta")$beta
rankings <- matrix(logical(), ncol=8, nrow=nrow(posteriorSamples))
## for each set of 8 posterior samples of each of the 8 water's latent quality, calculate if each sample is the maximum or not:
for (i in 1:nrow(posteriorSamples)) { rankings[i,] <- posteriorSamples[i,] >= max(posteriorSamples[i,]) }
df <- data.frame(Water=types, Superiority.p=round(digits=3,colMeans(rankings)))
df[order(df$Superiority.p, decreasing=TRUE),]
#                   Water Superiority.p
# 3                  Fiji         0.718
# 6         Poland Spring         0.145
# 1              Aquafina         0.110
# 8                  Voss         0.014
# 4 Great Value distilled         0.007
# 5      Nestle Pure Life         0.006
# 7             tap water         0.001
# 2                 Evian         0.000

plotBT(water, fit, types)

library(animation)
saveGIF(
    for (n in 7:nrow(water)) {
      df <- water[1:n,]
      fit <- fitBT(df)
      p <- plotBT(df, fit, types)
      print(p)
      },
    interval=0.6, ani.width = 1000, ani.height=800,
    movie.name = "tea-mineralwaters-bestarm-sequential.gif")

Means in descending order, with posterior probability of being the #1-top-ranked water (not the same thing as having a good mean ranking):

  1. Fiji (P = 0.72)

  2. Poland Spring (P = 0.15)

  3. Aquafina (P = 0.11)

  4. Evian (P = 0.00)

  5. Nestle Pure Life (P = 0.01)

  6. Great Value distilled (P = 0.01)

  7. Voss (P = 0.01)

  8. tap water (P = 0.00)

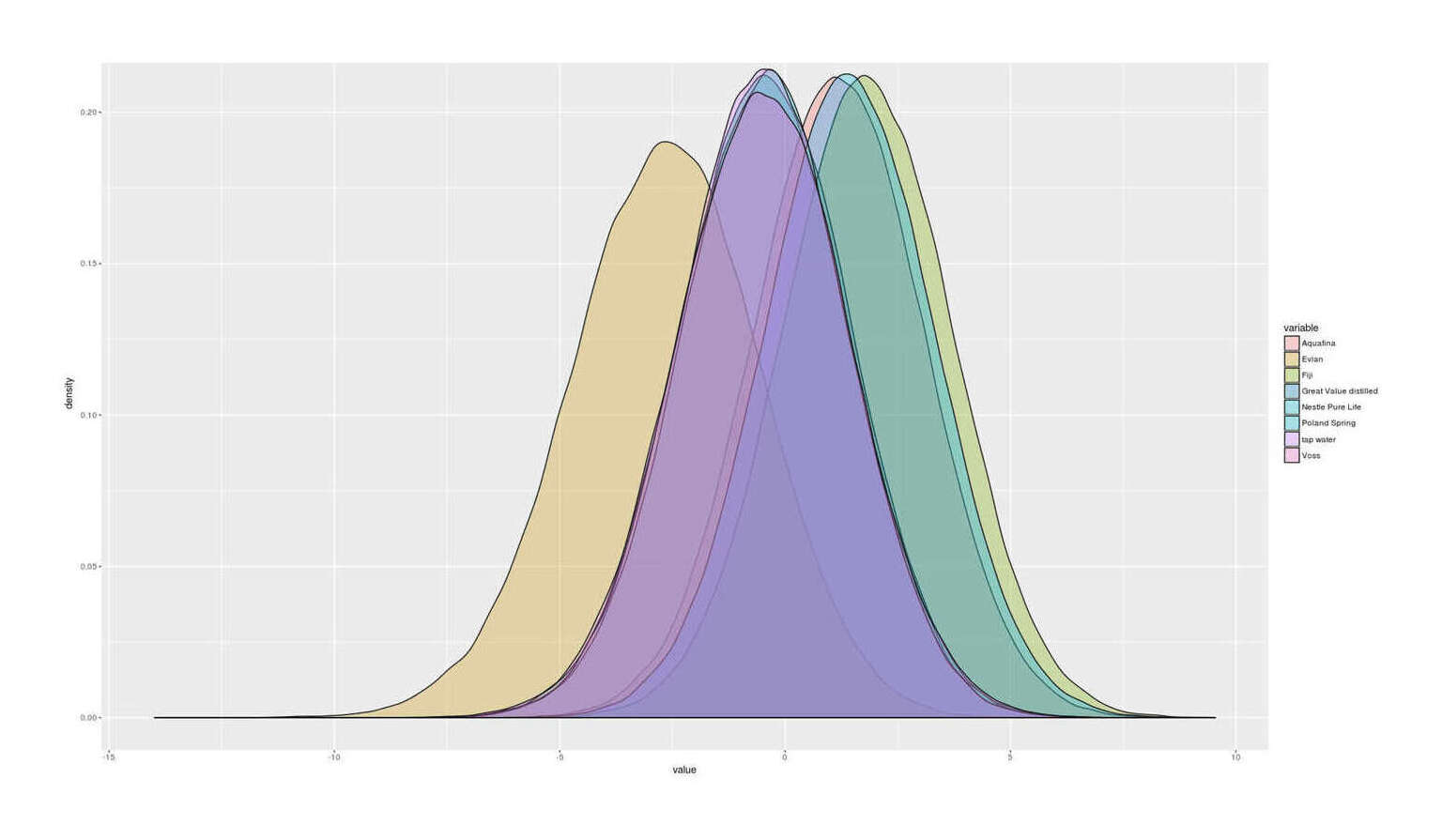
Results of n = 67 blinded randomized paired taste-testing comparisons of 8 mineral, distilled, and tap waters: final estimated posterior distributions of win probability in a comparison, showing the poor taste of Evian mineral water but likely similar tastes of most of the others.

Results of n = 67 blinded randomized paired taste-testing comparisons of 8 mineral, distilled, and tap waters: final estimated posterior distributions of win probability in a comparison, showing the poor taste of Evian mineral water but likely similar tastes of most of the others.

Animation of mineral water taste-test showing how the posterior distributions evolve over n = 7 to n = 67, guided by Bayesian best arm sampling.

For the first 7 comparisons, since I didn’t want to insert any informative priors about my expectations, the best arm choice would be effectively random, so to initialize it, I did a round-robin set of comparisons: put the waters into a quasi-random order ABCD, then compared A/B, B/C, C/D and so on. For the next 4 comparisons, I made a mistake in recording my data since I forgot that ‘1’ coded for the left water winning and ‘3’ for the right water winning, and so I had reversed the rankings and was actually doing a ‘worst-arm’ algorithm, as it were. After fixing that, the comparisons began focusing on Fiji and Poland Spring, eventually expanding to Aquafina as it improved in the rankings.

Comparing water turns out to be quite difficult. In some cases, a bad taste was quickly distinguishable—I quickly learned that Evian, Great Value distilled, and Nestle Pure Life had distinctly sour or metallic overtones which I disliked (but apparently enough people buy Evian & Nestle to make them viable in a Walmart!). Despite repeated sampling, I had a hard time ever distinguishing Poland Spring/Fiji/Aquafina/Voss, but I thought they might have been ever so slightly better than my tap water in a way I can’t verbalize except that they felt ‘cooler’ somehow.

By n = 41, Fiji continued to eke out a tiny lead over Poland Spring & Aquafina, but I ran out of it and could no longer run the best arm algorithm (since it would keep sampling Fiji). I was also running low on the Poland Spring. So at that point I went back to round-robin, this time using the order of posterior means.

With additional data, the wide posterior distributions began to contract around 0. At around n = 67, I was bored and not looking forward to sampling Evian/Great Value/Nestle many more times, and looking at the posterior distributions, it increasingly seemed like an exercise in futility—even after this much data, there was still only a 72% probability of correctly picking the best water.

Conclusion

Further testing would probably show Evian/Great Value/Nestle as worse than my tap water (amusingly enough), but be unable to meaningfully distinguish between my tap water and the decent ones, which answered the original question—no, the decent mineral waters & waters are almost indistinguishable under even the most optimal taste-testing conditions, would be less distinguishable when used in hot tea, and there was zero chance they were worth their enormous cost compared to my free tap water & were a scam as I expected. (After all, they are many times more expensive on a unit basis compared even to bottled water; the mineral contents are generally trivial fractions of RDAs at their highest; and they appear to be as equally likely to taste worse or better to the extent they taste different at all.)

I ended the experiment there, dumped the remaining water—except the remaining sealed Poland Spring bottles which are conveniently small, so I kept for use in my car—and recycled the containers.

  1. Additional amusing blind taste tests include wine, dog food vs pâté, and chocolate (data)—Valrhona is apparently overpriced.↩︎

  2. An interaction here implies that the effect happens only with the combination of two variables. On a chemical level, what would be going on to make good-tasting mineral water combined with good-tasting tea in distilled water turn into bad-tasting tea?↩︎

  3. “MRL—Minimum Reporting Limit. Where available, MRLs reflect the Method Detection Limits (MDLs) set by the U.S. Environmental Protection Agency or the Detection Limits for Purposes of Reporting (DLRs) set by the California Department of Health Services. These values are set by the agencies to reflect the minimum concentration of each substance that can be reliably quantified by applicable testing methods, and are also the minimum reporting thresholds applicable to the Consumer Confidence…ND—Not detected at or above the MRL.” –Nestle Pure Life2015↩︎

  4. See also Bubeck et al 2009, Audibert et al 2010, Gabillon et al 2011, Mellor2014, Jamieson & Nowak2014, Kaufmann et al 2014/↩︎

  5. This use of the posterior mean of the best arm distinguishes it from the simplest form of Thompson sampling for pairwise comparisons, which would be to simply Thompson sample each arm and compare the arms with the two highest samples, which is called “double Thompson sampling” by Wu & Liu2016. Double Thompson sampling achieves good regret but like regular Thompson sampling for MABs, doesn’t come with any proofs about best arm identification.↩︎

Similar Links

[Similar links by topic]