Spaced Repetition for Efficient Learning
Efficient memorization using the spacing effect: literature review of widespread applicability, tips on use & what it’s good for.
Spaced repetition is a centuries-old psychological technique for efficient memorization & practice of skills where instead of attempting to memorize by ‘cramming’, memorization can be done far more efficiently by instead spacing out each review, with increasing durations as one learns the item, with the scheduling done by software.
Because of the greater efficiency of its slow but steady approach, spaced repetition can scale to memorizing hundreds of thousands of items (while crammed items are almost immediately forgotten) and is especially useful for foreign languages & medical studies. (When there’s still too many to ever feasibly memorize, see my “anti-spaced repetition” proposal.)
I review what this technique is useful for, some of the large research literature on it and the testing effect (up to ~2013, primarily), the available software tools and use patterns, and miscellaneous ideas & observations on it.
One of the most fruitful areas of computing is making up for human frailties. They do arithmetic perfectly because we can’t1. They remember terabytes because we’d forget. They make the best calendars, because they always check what there is to do today. Even if we do not remember exactly, merely remembering a reference can be just as good, like the point of reading a manual or textbook all the way through: it is not to remember everything that is in it for later but to later remember that something is in it (and skimming them, you learn the right words to search for when you actually need to know more about a particular topic).
We use any number of such neuroprosthetics2, but there are always more to be discovered. They’re worth looking for because they are so valuable: a shovel is much more effective than your hand, but a power shovel is orders of magnitude better than both - even if it requires training and expertise to use.
Spacing Effect
You can get a good deal from rehearsal,
If it just has the proper dispersal.
You would just be an ass,
To do it en masse,
Your remembering would turn out much worsal.Ulrich Neisser3
My current favorite prosthesis is the class of software that exploits the spacing effect, a centuries-old observation in cognitive psychology, to achieve results in studying or memorization much better than conventional student techniques; it is, alas, obscure4.
The spacing effect essentially says that if you have a question (“What is the fifth letter in this random sequence you learned?”), and you can only study it, say, 5 times, then your memory of the answer (‘e’) will be strongest if you spread your 5 tries out over a long period of time - days, weeks, and months. One of the worst things you can do is blow your 5 tries within a day or two. You can think of the ‘forgetting curve’ as being like a chart of a radioactive half-life: each review bumps your memory up in strength 50% of the chart, say, but review doesn’t do much in the early days because the memory simply hasn’t decayed much! (Why does the spacing effect work, on a biological level? There are clear neurochemical differences between massed and spaced in animal models with spacing (>1 hour) enhancing long-term potentiation but not massed5, but the why and wherefore - that’s an open question; see the concept of memory traces or the sleep studies.) A graphical representation of the forgetting curve:
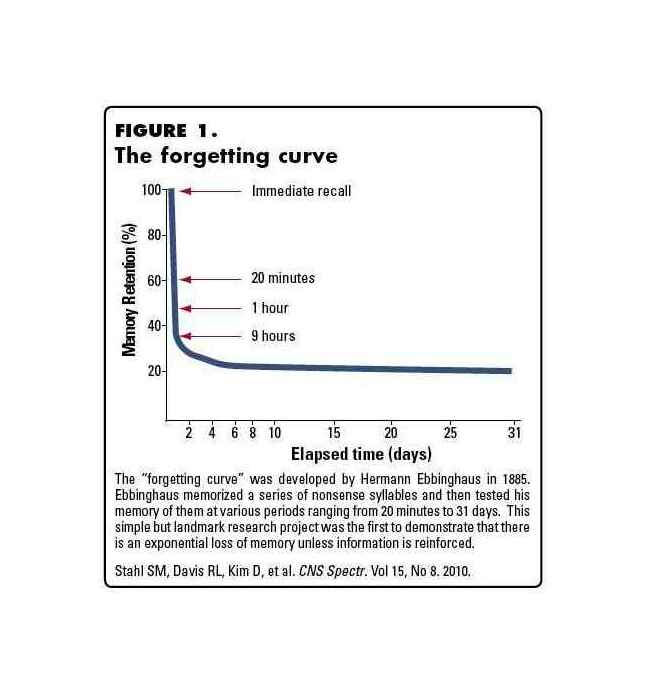
et al 2010; CNS Spectrums
Even better, it’s known that active recall is a far superior method of learning than simply passively being exposed to information.6 Spacing also scales to huge quantities of information; gambler/financier Edward O. Thorp harnessed “spaced learning” when he was a physics grad student “in order to be able to work longer and harder”7, and Roger Craig set multiple records on the quiz show Jeopardy! 2010–201115ya in part thanks to using Anki to memorize chunks of a collection of >200,000 past questions8; a later Jeopardy winner, Arthur Chu, also used spaced repetition9. Med school students (who have become a major demographic for SRS due to the extremely large amounts of factual material they are expected to memorize during medical school) usually have thousands of cards, especially if using pre-made decks (more feasible for medicine due to fairly standardized curriculums & general lack of time to make custom cards). Foreign-language learners can easily reach 10-30,000 cards; one Anki user reports a deck of >765k automatically-generated cards filled with Japanese audio samples from many sources (“Youtube videos, video games, TV shows, etc”).
A graphic might help; imagine here one can afford to review a given piece of information a few times (one is a busy person). By looking at the odds we can remember the item, we can see that cramming wins in the short term, but unexercised memories decay so fast that after not too long spacing is much superior:
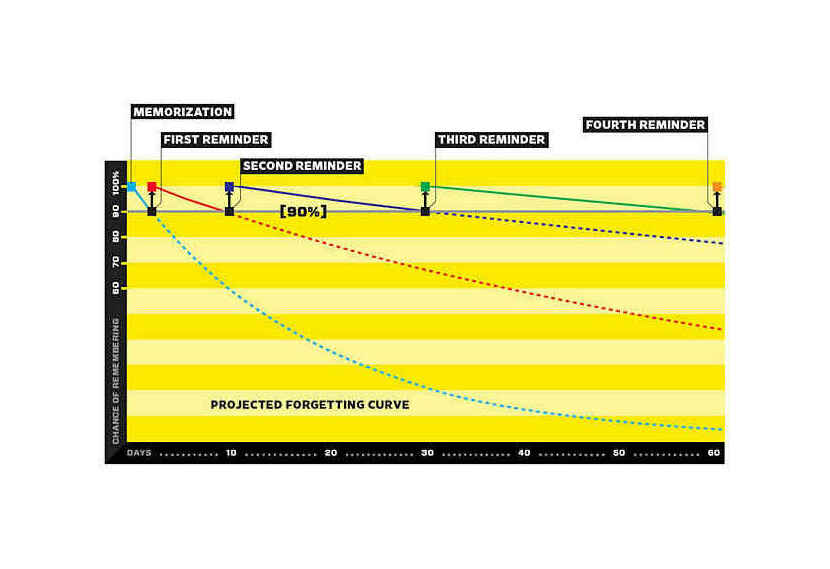
Wired (original, Wozniak?); massed vs spaced (alternative)
It’s more dramatic if we look at a video visualizing decay of a corpus of memory with random review vs most-recent review vs spaced review.
If You’re so Good, Why Aren’t You Rich
Most people find the concept of programming obvious, but the doing impossible.10
Of course, the latter strategy (cramming) is precisely what students do. They cram the night before the test, and a month later can’t remember anything. So why do people do it? (I’m not innocent myself.) Why is spaced repetition so dreadfully unpopular, even among the people who try it once?11

Scumbag Brain meme: knows everything when cramming the night before the test / and forgets everything a month later
Because it does work. Sort of. Cramming is a trade-off: you trade a strong memory now for weak memory later. (Very weak12.) And tests are usually of all the new material, with occasional old questions, so this strategy pays off! That’s the damnable thing about it - its memory longevity & quality are, in sum, less than that of spaced repetition, but cramming delivers its goods now13. So cramming is a rational, if short-sighted, response, and even SRS software recognize its utility & support it to some degree14. (But as one might expect, if the testing is continuous and incremental, then the learning tends to also be long-lived15; I do not know if this is because that kind of testing is a disguised accidental spaced repetition system, or the students/subjects simply studying/acting differently in response to small-stakes exams.) In addition to this short-term advantage, there’s an ignorance of the advantages of spacing and a subjective illusion that the gains persist1617 (cf. 201218, 2014, et al 2013, et al 2019); from 2009’s study of GRE vocab (emphasis added):
Across experiments, spacing was more effective than massing for 90% of the participants, yet after the first study session, 72% of the participants believed that massing had been more effective than spacing….When they do consider spacing, they often exhibit the illusion that massed study is more effective than spaced study, even when the reverse is true (Dunlosky & Nelson, 1994; Kornell & Bjork, 200818yaa; 2001; Zechmeister & Shaughnessy, 1980).
As one would expect if the testing and spacing effects are real things, students who naturally test themselves and study well in advance of exams tend to have higher GPAs.19 If we interpret questions as tests, we are not surprised to see that 1-on-1 tutoring works dramatically better than regular teaching and that tutored students answer orders of magnitude more questions20.
This short-term perspective is not a good thing in the long term, of course. Knowledge builds on knowledge; one is not learning independent bits of trivia. Richard Hamming recalls in “You and Your Research” that “You observe that most great scientists have tremendous drive….Knowledge and productivity are like compound interest.”
Knowledge needs to accumulate, and flashcards with spaced repetition can aid in just that accumulation, fostering steady review even as the number of cards and intellectual prerequisites mounts into the thousands.
This long term focus may explain why explicit spaced repetition is an uncommon studying technique: the pay-off is distant & counterintuitive, the cost of self-control near & vivid. (See hyperbolic discounting.) It doesn’t help that it’s pretty difficult to figure out when one should review - the optimal point is when you’re just about to forget about it, but that’s the kicker: if you’re just about to forget about it, how are you supposed to remember to review it? You only remember to review what you remember, and what you already remember isn’t what you need to review!21
The paradox is resolved by letting a computer handle all the calculations. We can thank Hermann Ebbinghaus for investigating in such tedious detail than we can, in fact, program a computer to calculate both the forgetting curve and optimal set of reviews22. This is the insight behind spaced repetition software: ask the same question over and over, but over increasing spans of time. You start with asking it once every few days, and soon the human remembers it reasonably well. Then you expand intervals out to weeks, then months, and then years. Once the memory is formed and dispatched to long-term memory, it needs but occasional exercise to remain hale and hearty23 - I remember well the large dinosaurs made of cardboard for my 4th or 5th birthday, or the tunnel made out of boxes, even though I recollect them once or twice a year at most.
Literature Review
But don’t take my word for it - Nullius in verba! We can look at the science. Of course, if you do take my word for it, you probably just want to read about how to use it and all the nifty things you can do, so I suggest you skip all the way down to that section. Everyone else, we start at the beginning:
Background: Testing Works!
“If you read a piece of text through twenty times, you will not learn it by heart so easily as if you read it ten times while attempting to recite from time to time and consulting the text when your memory fails.” –The New Organon, Francis Bacon
The testing effect is the established psychological observation that the mere act of testing someone’s memory will strengthen the memory (regardless of whether there is feedback). Since spaced repetition is just testing on particular days, we ought to establish that testing works better than regular review or study, and that it works outside of memorizing random dates in history. To cover a few papers:
Allen, G.A., Mahler, W.A., & Estes, W.K. (196957ya). “Effects of recall tests on long-term retention of paired associates”. Journal of Verbal Learning and Verbal Behavior, 8, 463-470
1 test results in memories as strong a day later as studying 5 times; intervals improve retention compared to massed presentation.
Karpicke & Roediger (200323ya). “The Critical Importance of Retrieval for Learning”
In learning Swahili vocabulary, students were given varying routines of testing or studying or testing and studying; this resulted in similar scores during the learning phase. Students were asked to predict what percentage they’d remember (average: 50% over all groups). One week later, the students who tested remembered ~80% of the vocabulary versus ~35% for non-testing students. Some students were tested or studied more than others; diminishing returns set in quickly once the memory had formed the first day. Students reported rarely testing themselves and not testing already learned items.
Lesson: again, testing improves memory compared to studying. Also, no student knows this.
Roediger & Karpicke (200620yaa). “Test-Enhanced Learning: Taking Memory Tests Improves Long-Term Retention”
Students were tested (with no feedback) on reading comprehension of a passage over 5 minutes, 2 days, and 1 week. Studying beat testing over 5 minutes, but nowhere else; students believed studying superior to testing over all intervals. At 1 week, testing scores were ~60% versus ~40%.
Lesson: testing improves memory compared to studying. Everyone (teachers & students) ‘knows’ the opposite.
Karpicke & Roediger (200620yaa). “Expanding retrieval promotes short-term retention, but equal interval retrieval enhances long-term retention”
General scientific prose comprehension; from 2006b: “After 2 days, initial testing produced better retention than restudying (68% versus 54%), and an advantage of testing over restudying was also observed after 1 week (56% versus 42%).”
Roediger & Karpicke (200620yab). “The Power of Testing Memory: Basic Research and Implications for Educational Practice”
Literature review; 7 studies before 194185ya demonstrating testing improves retention, and 6 afterwards. See also the reviews “Spacing Learning Events Over Time: What the Research Says” & “Using spacing to enhance diverse forms of learning: Review of recent research and implications for instruction”, et al 2012.
et al 2008, “Examining the Testing Effect with Open- and Closed-Book Tests”
As with #2, the purer forms of testing (in this case, open-book versus closed-book testing) did better over the long run, and students were deluded about what worked best.
Bangert- et al 1991. “Effects of frequent classroom testing”
Meta-analysis of 35 studies (1929–60198937ya) varying tests during school semesters. 29 found benefits; 5 found negatives; 1 null result. Meta-study found large benefits to testing even once, then diminishing returns.
2006, “Impact of self-assessment questions and learning styles in Web-based learning: a randomized, controlled, crossover trial”; final scores were higher when the doctors (residents) learned with questions.
2009, “The Effect of Online Chapter Quizzes on Exam Performance in an Undergraduate Social Psychology Course” (“This study examined the effectiveness of compulsory, mastery-based, weekly reading quizzes as a means of improving exam and course performance. Completion of reading quizzes was related to both better exam and course performance.”); see also et al 2012.
2013, “Effect of Repeated Testing on the Development of Secondary Language Proficiency”
2013, “Taking the Testing Effect Beyond the College Freshman: Benefits for Lifelong Learning”; verifies testing effect in older adults has similar effect size as younger
2013, “Test-enhanced learning”
et al 2021, “Testing (Quizzing) Boosts Classroom Learning: A Systematic And Meta–Analytic Review”
(One might be tempted to object that testing works for some learning styles, perhaps verbal styles. This is an unsupported assertion inasmuch as the experimental literature on learning styles is poor and the existing evidence mixed that there are such things as learning styles.24)
Subjects
The above studies often used pairs of words or words themselves. How well does the testing effect generalize?
Materials which benefited from testing:
foreign vocabulary (eg. 2003, et al 2009, et al 200725, de la 2012)
GRE materials (like vocab, 2009); prose passages on general scientific topics (Karpicke & Roediger, 200620yaa; Pashler et al, 200323ya)
trivia (1991)
elementary & middle school lessons with subjects such as biographical material and science (1917; 193926 and 201227, respectively)
et al 2008: short-answer tests superior on textbook passages
history textbooks; retention better with initial short-answer test rather than multiple choice (1982)
1975 also found better retention compared to multiple-choice or recognition problems
Duchastel & Nungester, 1981: 6 months after testing, testing beat studying in retention of a history passage
1981: free recall decisively beat short-answer & multiple choice for reading comprehension of a history passage
1989: free recall self-test beat recognition or Cloze deletions; subject matter was the labels for parts of flowers
et al 2007: prose passages; initial short answer testing produced superior results 3 days later on both multiple choice and short answer tests
2002: tests in 2 psychology courses, introductory & memory/learning; “80% versus 74% for the introductory psychology course and 89% versus 80% for the learning and memory course”28
This covers a pretty broad range of what one might call ‘declarative’ knowledge. Extending testing to other fields is more difficult and may reduce to ‘write many frequent analyses, not large ones’ or ‘do lots of small exercises’, whatever those might mean in those fields:
A third issue, which relates to the second, is whether our proposal of testing is really appropriate for courses with complex subject matters, such as the philosophy of Spinoza, Shakespeare’s comedies, or creative writing. Certainly, we agree that most forms of objective testing would be difficult in these sorts of courses, but we do believe the general philosophy of testing (broadly speaking) would hold-students should be continually engaged and challenged by the subject matter, and there should not be merely a midterm and final exam (even if they are essay exams). Students in a course on Spinoza might be assigned specific readings and thought-provoking essay questions to complete every week. This would be a transfer-appropriate form of weekly ‘testing’ (albeit with take-home exams). Continuous testing requires students to continuously engage themselves in a course; they cannot coast until near a midterm exam and a final exam and begin studying only then.29
Downsides
Testing does have some known flaws:
interference in recall - ability to remember tested items drives out ability to remember similar untested items
Most/all studies were in laboratory settings and found relatively small effects:
In sum, although various types of recall interference are quite real (and quite interesting) phenomena, we do not believe that they compromise the notion of test-enhanced learning. At worst, interference of this sort might dampen positive testing effects somewhat. However, the positive effects of testing are often so large that in most circumstances they will overwhelm the relatively modest interference effects.
multiple choice tests can accidentally lead to ‘negative suggestion effects’ where having previously seen a falsehood as an item on the test makes one more likely to believe it.
This is mitigated or eliminated when there’s quick feedback about the right answer (see 2008 “Feedback enhances the positive effects and reduces the negative effects of multiple-choice testing”). Solution: don’t use multiple choice; inferior in testing ability to free recall or short answers, anyway.
Neither problem seems major.
Distributed
A lot depends on when you do all your testing. Above we saw some benefits to testing a lot the moment you learn something, but the same number of tests could be spread out over time, to give us the spacing effect or spaced repetition. There are hundreds of studies involving the spacing effect:
et al 2006 is a review of 184 articles with 317 experiments; other reviews include:
1928, “Factors influencing the relative economy of massed and distributed practice in learning”
1989, “Spacing effects and their implications for theory and practice”
et al 2010, “Spacing and testing effects: A deeply critical, lengthy, and at times discursive review of the literature”
1999, “A meta-analytic review of the distribution of practice effect: Now you see it, now you don’t”
Almost unanimously they find spacing out tests is superior to massed testing when the final test/measurement is conducted days or years later30, although the mechanism isn’t clear31. Besides all the previously mentioned studies, we can throw in:
Peterson, L. R., Wampler, R., Kirkpatrick, M., & Saltzman, D. (196363ya). “Effect of spacing presentations on retention of a paired associate over short intervals”. Journal of Experimental Psychology, 66(2), 206-209
Glenberg, A. M. (197749ya). “Influences of retrieval processes on the spacing effect in free recall”. Journal of Experimental Psychology: Human Learning and Memory, 3(3), 282-294
et al 1989, “Age-related differences in the impact of spacing, lag and retention interval”. Psychology and Aging, 4, 3-9
The research literature focuses extensively on the question of what kind of spacing is best and what this implies about memory: a spacing that has static fixed intervals or a spacing which expands? This is important for understanding memory and building models of it, and would be helpful for integrating spaced repetition into classrooms (for example, 2013’s 10 minutes studying / 10 minutes break schedule, repeating the same material 3 times, designed to trigger LTM formation on that block of material?) But for practical purposes, this is uninteresting; to sum it up, there are many studies pointing each way, and whatever difference in efficiency exists, is minimal. Most existing software follows SuperMemo in using an expanding spacing algorithm, so it’s not worth worrying about; as Mnemosyne developer Peter Bienstman says, it’s not clear the more complex algorithms really help32, and the Anki developers were concerned about the complexity, difficulty of reimplementing SM’s proprietary algorithms, lack of substantial gains, & larger errors SM3+ risks attempting to be more optimal. So too here.
For those interested, 3 of the studies that found fixed spacings better than expanding:
Carpenter, S. K., & DeLosh, E. L. (200521ya). “Application of the testing and spacing effects to name learning”. Applied Cognitive Psychology, 19, 619-63633
Logan, J. M. (200422ya). Spaced and expanded retrieval effects in younger and older adults. Unpublished doctoral dissertation, Washington University, St. Louis, MO
This thesis is interesting inasmuch as Logan found that young adults did considerably worse with an expanding spacing after a day.
Karpicke & Roediger, 200620yaa
The fixed vs expanding issue aside, a list of additional generic studies finding benefits to spaced vs massed:
et al 2006 (large review used elsewhere in this page)
2006a
2006. “The effects of over-learning and distributed practice on the retention of mathematics knowledge”. Applied Cognitive Psychology, 20: 1209–1224 (see also 2007, et al 2005)
et al 2005. “Distributed and Massed Practice: From Laboratory to Classroom”
Keppel, Geoffrey. “A Reconsideration of the Extinction-Recovery Theory”. Journal of Verbal Learning & Verbal Behavior. 6(4) 196759ya, 476-486
A week later, the massed reviewers went from 5.9 correct → 2.1; the spaced reviewers went from 5.5 → 5.0. (Note the usual observation: massed was initially better, and later much worse, less than half as good.)
-
Four days after the 2 high school groups memorized 16 French words, the spaced group remembered 15 and the massed 11.
1985, “The effect of expanded versus massed practice on the retention of multiplication facts and spelling lists”34
A test immediately following the training showed superior performance for the distributed group (70% correct) compared to the massed group (53% correct). These results seem to show that the spacing effect applies to school-age children and to at least some types of materials that are typically taught in school.35
1999, “A meta-analytic review of the distribution of practice effect: Now you see it, now you don’t”:
According to Donovan & Radosevich’s meta-analysis of spacing studies, the effect size for the spacing effect is d = 0.42. This means that the average person getting distributed training remembers better than about 67% of the people getting massed training. This effect size is nothing to sneeze at-in education research, effect sizes as low as d = 0.25 are considered “practically significant”, while effect sizes above d = 1 are rare.36
In one meta-analysis by 1999, for instance, the size of the spacing effect declined sharply as conceptual difficulty of the task increased from low (eg. rotary pursuit) to average (eg. word list recall) to high (eg. puzzle). By this finding, the benefits of spaced practise may be muted for many mathematics tasks.37
The Donovan meta-analysis notes that the effect size is smaller in studies with better methodology, but still important.
Bahrick, Harry P; Phelphs, Elizabeth. “Retention of Spanish vocabulary over 8 years”. Journal of Experimental Psychology: Learning, Memory, & Cognition. Vol 13(2) April 198739ya, 344-349; the extremely long delay after the initial training period makes this particularly interesting:
Harry Bahrick and Elizabeth Phelps (198739ya) examined the retention of 50 Spanish vocabulary words after an eight-year delay. Subjects were divided into three groups. Each practiced for seven or eight sessions, separated by a few minutes, a day, or 30 days. In each session, subjects practiced until they could produce the list perfectly one time….Eight years later, people in the no-delay group could recall 6% of the words, people in the one-day delay group could remember 8%, and those in the 30-day group averaged 15%. Everyone also took a multiple choice test, and again, the spacing effect was observed. The no-delay group scored 71%, the one-day group scored 80%, and the 30-day group scored 83%.
…Bahrick and his colleagues varied both the spacing of practice and the amount of practice. Practice sessions were spaced 14, 28, or 56 days apart, and totaled 13 or 26 sessions. They tested subjects’ memory one, two, three, and five years after training. Once again, it took a bit longer to reach the criterion within each session when practice sessions were spaced farther apart, but again, this small investment paid dividends years later. It didn’t matter whether testing occurred at one, two, three, or five years after practice-the 56-day group always remembered the most, the 28-day group was next, and the 14-day group remembered the least. Further, the effect was quite large. If words were practiced every 14 days, you needed twice as much practice to reach the same level of performance as when words were practiced every 56 days!
et al 2003; “Is Temporal Spacing of Tests Helpful Even When It Inflates Error Rates?”
Long intervals between tests necessarily means you will often err; errors were thought to intrinsically reduce learning. While the extra errors do damage accuracy in the short-run, the long intervals are powerful enough that they still win.
works in ill subpopulations:
works on short-term review conducted with Alzheimer’s patients; spacing used on the scale of seconds and minutes, with modest success in teaching object locations or daily tasks to do38:
Camp, C. J. (198937ya). “Facilitation of new learning in Alzheimer’s disease”. In G. C. Gilmore, P. J. Whitehouse, & M. L. Wykle (Eds.), Memory, aging, and dementia (pp. 212-225)
Camp, C. J., & McKitrick, L. A. (199234ya). “Memory interventions in Alzheimer’s-type dementia populations: Methodological and theoretical issues”. In R. L. West & J. D. Sinnott (Eds.), Everyday memory and aging: Current research and methodology (pp. 152-172) -
works with traumatic brain injury; et al 2009, “Application of the spacing effect to improve learning and memory for functional tasks in traumatic brain injury: a pilot study”
and multiple sclerosis; et al 2009, “A functional application of the spacing effect to improve learning and memory in persons with multiple sclerosis”
math39:
multiplication (1985)
permuting a sequence (2006)on
calculating the volume of polyhedrons (2007)
statistics (1984)
pre-calculus (199740 but there’s a related null ‘calculus I’ result as well) and algebra (2002, 2013; possible null, 2013)
medicine (2009, et al 2012; 2009, a 2 year followup to et al 2007 and Kerfoot has a number of other relevant studies; et al 2013) and surgery ( et al 2006, “Teaching Surgical Skills: What Kind of Practice Makes Perfect? A Randomized, Controlled Trial”, distributed practice of microvascular suturing; et al 2014)
introductory psychology (2006, “Encouraging Distributed Study: A Classroom Experiment on the Spacing Effect”41. Teaching of Psychology, 33, 249-252)
8th-grade American history (Carpenter, Pashler, and 2009)
learning to read with phonics ( et al 2005)
music (2009)
biology (middle school; 2013)
statistics (introductory; et al 2015)
memorizing website passwords (2014, et al 2014, 2017)
possibly not Australian constitutional law ( et al 2015)
Generality of Spacing Effect
We have already seen that spaced repetition is effective on a variety of academic fields and mediums. Beyond that, spacing effects can be found in:
various “domains (eg. learning perceptual motor tasks or learning lists of words)”42 such as spatial43
“across species (eg. rats, pigeons, and humans [or flies or bumblebees, and sea slugs, et al 1972 & et al 2002])”
“across age groups [infancy44, childhood45, adulthood46, the elderly47] and individuals with different memory impairments”
“and across retention intervals of seconds48 [to days49] to months” (we have already seen studies using years)
The domains are limited, however. et al 2006:
[1995, reviewing 120 articles] concluded that longer ISIs facilitate learning of verbal information (eg. spelling50) and motor skills (eg. mirror tracing); in each case, over 80% of studies showed a distributed practice benefit. In contrast, only one third of intellectual skill (eg. math computation) studies showed a benefit from distributed practice, and half showed no effect from distributed practice.
…[1999] The largest effect sizes were seen in low rigor studies with low complexity tasks (eg. rotary pursuit, typing, and peg reversal), and retention interval failed to influence effect size. The only interaction Donovan and Radosevich examined was the interaction of ISI and task domain. It is important to note that task domain moderated the distributed practice effect; depending on task domain and lag, an increase in ISI either increased or decreased effect size. Overall, Donovan and Radosevich found that increasingly distributed practice resulted in larger effect sizes for verbal tasks like free recall, foreign language, and verbal discrimination, but these tasks also showed an inverse-U function, such that very long lags produced smaller effect sizes. In contrast, increased lags produced smaller effect sizes for skill tasks like typing, gymnastics, and music performance.
Skills like gymnastics and music performance raise an important point about the testing effect and spaced repetition: they are for the maintenance of memories or skills, they do not increase it beyond what was already learned. If one is a gifted amateur when one starts reviewing, one remains a gifted amateur. Ericsson covers what is necessary to improve and attain new expertise: deliberate practice51. From “The Role of Deliberate Practice”:
The view that merely engaging in a sufficient amount of practice—regardless of the structure of that practice—leads to maximal performance, has a long and contested history. In their classic studies of Morse Code operators, Bryan and Harter (1897, 1899) identified plateaus in skill acquisition, when for long periods subjects seemed unable to attain further improvements. However, with extended efforts, subjects could restructure their skill to overcome plateaus…Even very experienced Morse Code operators could be encouraged to dramatically increase their performance through deliberate efforts when further improvements were required…More generally, Thorndike (1921105ya) observed that adults perform at a level far from their maximal level even for tasks they frequently carry out. For instance, adults tend to write more slowly and illegibly than they are capable of doing…The most cited condition [for optimal learning and improvement of performance] concerns the subjects’ motivation to attend to the task and exert effort to improve their performance…The subjects should receive immediate informative feedback and knowledge of results of their performance…In the absence of adequate feedback, efficient learning is impossible and improvement only minimal even for highly motivated subjects. Hence mere repetition of an activity will not automatically lead to improvement in, especially, accuracy of performance…In contrast to play, deliberate practice is a highly structured activity, the explicit goal of which is to improve performance. Specific tasks are invented to overcome weaknesses, and performance is carefully monitored to provide cues for ways to improve it further. We claim that deliberate practice requires effort and is not inherently enjoyable.
Motor Skills
It should be noted that reviews conflict on how much spaced repetition applies to motor skills; 1988 find benefits, while 1987 and earlier do not. The difference may be that simple motor tasks benefit from spacing as suggested by 1979 (benefits to a randomized/spaced schedule), while complex ones where the subject is already operating at his limits do not benefit, suggested by 2002. 2009 mentions some divergent studies:
The contextual interference hypothesis (Shea and 1979, 1966 [“Facilitation and interference” in Acquisition of skill]) predicted the blocked condition would exhibit superior performance immediately following practice (acquisition) but the random condition would perform better at delayed retention testing. This hypothesis is generally consistent in laboratory motor learning studies (eg. 1983, 2004), but less consistent in applied studies of sports skills (with a mix of positive & negative eg. 1997, et al 1994, 2013) and fine-motor skills ( et al 2005, Ste- et al 2004).
Some of the positive spaced repetition studies (from 2012):
Perhaps even prior to the empirical work on cognitive learning and the spacing effect, the benefits of spaced study had been apparent in an array of motor learning tasks, including maze learning (1912), typewriting (1915), archery (1915), and javelin throwing (1916; see 1928, for a larger review of the motor learning tasks which reap benefits from spacing; see also 1996, for a more recent review of motor learning tasks). Thus, as in the cognitive literature, the study of practice distribution in the motor domain is long established (see reviews by 1987; 2005), and most interest has centered around the impact of varying the separation of learning trials of motor skills in learning and retention of practiced skills. 1988 conducted a review and meta-analysis of studies on distribution of practice, and they concluded that massing of practice tends to depress both immediate performance and learning, where learning is evaluated at some removed time from the practice period. Their main finding was, as in the cognitive literature, that learning was relatively stronger after spaced than after massed practice (although see 1988; 1988; et al 1988 for criticisms of the review)…Probably the most widely cited example is 1978’s study concerning how optimally to teach postal workers to type. They had learners practice once a day or twice a day, and for session lengths of either 1 or 2 h at a time. The main findings were that learners took the fewest cumulative hours of practice to achieve a performance criterion in their typing when they were in the most distributed practice condition. This finding provides clear evidence for the benefits of spacing practice for enhancing learning. However, as has been pointed out (; 2005), there is also trade-off to be considered in that the total elapsed time (number of days) between the beginning of practice and reaching criterion was substantially longer for the most spaced condition….The same basic results have been repeatedly demonstrated in the decades since (see reviews by 1990; 2004), and with a wide variety of motor tasks including different badminton serves (1986), rifle shooting (Boyce & Del 1990), a pre-established skill, baseball batting ( et al 1994), learning different logic gate configurations ( et al 1989; 1990), for new users of automated teller machines (2000), and for solving mathematical problems as might appear in a class homework (2007; Le 2008; 2010).
Culler, E. A. (1912114ya). “The effect of distribution of practice upon learning”. Journal of Philosophical Psychology, 9, 580-583
Pyle, W. H. (1915111ya). “Concentrated versus distributed practice”
Murphy, H. H. (1916110ya). “Distributions of practice periods in learning”. Journal of Educational Psychology, 7, 150-162
Adams, J. A. (198739ya). “Historical review and appraisal of research on the learning, retention, and transfer of human motor skills”
Schmidt, R. A., & Lee, T. D. (200521ya). Motor control and learning: A behavioral emphasis (4th ed.). Urbana-Champaign: Human Kinetics
Lee, T. D., & Genovese, E. D. (198838ya). “Distribution of practice in motor skill acquisition: Learning and performance effects reconsidered”. Research Quarterly for Exercise and Sport, 59, 277-287
Ammons, R. B. (198838ya). “Distribution of practice in motor skill acquisition: A few questions and comments”. Research Quarterly for Exercise and Sport, 59, 288-290
Christina, R. W., & Shea, J. B. (198838ya). “The limitations of generalization based on restricted information”. Research Quarterly for Exercise and Sport, 59, 291-297
Newell, K. M., Antoniou, A., & Carlton, L. G. (198838ya). “Massed and distributed practice effects: Phenomena in search of a theory?” Research Quarterly for Exercise and Sport, 59, 308-313
Lee, T. D., & Wishart, L. R. (200521ya). “Motor learning conundrums (and possible solutions)”
Lee, T. D., & Simon, D. A. (200422ya). “Contextual interference”
Goode, S., & Magill, R. A. (198640ya). “Contextual interference effects in learning three badminton serves”. Research Quarterly for Exercise and Sport, 57, 308-314
Boyce,, & Del Rey, P. (199036ya). “Designing applied research in a naturalistic setting using a contextual interference paradigm”. Journal of Human Movement Studies, 18, 189-200
et al 1994, “Contextual interference effects with skilled baseball players”
Carlson, R. A., & Yaure, R. G. (199036ya). “Practice schedules and the use of component skills in problem solving”
Carlson, R. A., Sullivan, M. A., & Schneider, W. (198937ya). “Practice and working memory effects in building procedural skill”
Jamieson,, & Rogers, W. A. (200026ya). “Age-related effects of blocked and random practice schedules on learning a new technology”
Le Blanc, K. & Simon, D. A. (200818ya). “Mixed practice enhances retention and JOL accuracy for mathematical skills”. Poster presented at the 200818ya annual meeting of the Psychonomic Society, Chicago, IL
et al 2016, “Motor Skills Are Strengthened through Reconsolidation”
et al 1993, “The Effects of Variable Practice on the Performance of a Basketball Skill”
In this vein, it’s interesting to note that interleaving may be helpful for tasks with a mental component as well: et al 2003, et al 2011, and according to et al 2013 the rates at which Xbox Halo: Reach video game players advance in skill matches nicely predictions from distribution: players who play 4–8 matches a week advance more in skill per match, than players who play more (distributed); but advance slower per week than players who play many more matches / massed. (See also 2016.)
Abstraction
Another potential objection is to argue52 that spaced repetition inherently hinders any kind of abstract learning and thought because related materials are not being shown together - allowing for comparison and inference - but days or months apart. Ernst A. Rothkopf: “Spacing is the friend of recall, but the enemy of induction” (2008, p. 585). This is plausible based on some of the early studies53 but the 4 recent studies I know of directly examining the issue both found spaced repetition helped abstraction as well as general recall:
2008a, “Learning concepts and categories: Is spacing the ‘enemy of induction’?” Psychological Science, 19, 585-592
Vlach, H. A., Sandhofer, C. M., & Kornell, N. (200818ya). “The spacing effect in children’s memory and category induction”. Cognition, 109, 163-167
Kornell, N., Castel, A. D., Eich, T. S., & Bjork, R. A. (201016ya). “Spacing as the friend of both memory and induction in younger and older adults”. Psychology and Aging, 25, 498-503
2012, “Distributing Learning Over Time: The Spacing Effect in Children’s Acquisition and Generalization of Science Concepts”, Child Development
2012, “The spacing effect in inductive learning”; includes:
replication of 2008
et al 2011
unknown paper currently in peer review
et al 2013, “Effects of Spaced versus Massed Training in Function Learning”
et al 2014: 1, 2; et al 2019: “A randomized controlled trial of interleaved mathematics practice”
et al 2014, “Equal spacing and expanding schedules in children’s categorization and generalization”
Gluckman et al, “Spacing Simultaneously Promotes Multiple Forms of Learning in Children’s Science Curriculum”
Review Summary
To bring it all together with the gist:
testing is effective and comes with minimal negative factors
expanding spacing is roughly as good as or better than (wide) fixed intervals, but expanding is more convenient and the default
testing (and hence spacing) is best on intellectual, highly factual, verbal domains, but may still work in many low-level domains
the research favors questions which force the user to use their memory as much as possible; in descending order of preference:
free recall
short answers
multiple-choice
Cloze deletion
recognition
the research literature is comprehensive and most questions have been answered - somewhere.
the most common mistakes with spaced repetition are
formulating poor questions and answers
assuming it will help you learn, as opposed to maintain and preserve what one already learned54. (It’s hard to learn from cards, but if you have learned something, it’s much easier to then devise a set of flashcards that will test your weak points.)
Using It
One doesn’t need to use SuperMemo, of course; there are plenty of free alternatives. I like Mnemosyne (homepage) myself - Free, packaged for Ubuntu Linux, easy to use, free mobile client, long track record of development and reliability (I’ve used it since ~2008). But the SRS Anki is also popular, and has advantages in being more feature-rich and a larger & more active community (and possibly better support for East Asian language material and a better but proprietary mobile client).
OK, but what does one do with it? It’s a surprisingly difficult question, actually. It’s akin to “the tyranny of the blank page” (or blank wiki); now that I have all this power - a mechanical golem that will never forget and never let me forget whatever I chose to - what do I choose to remember?
How Much To Add
The most difficult task, beyond that of just persisting until the benefits become clear, is deciding what’s valuable enough to add in. In a 3 year period, one can expect to spend “30–40 seconds” on any given item. The long run theoretical predictions are a little hairier. Given a single item, the formula for daily time spent on it is Time = 1⁄500 × nthYear−1.5 + 1⧸30,000. During our 20th year, we would spend t = 1⁄500 × 20−1.5 + 1⧸3,000, or 3.557e-4 minutes a day. This is the average daily time, so to recover the annual time spent, we simply multiply by 365. Suppose we were interested in how much time a flashcard would cost us over 20 years. The average daily time changes every year (the graph looks like an exponential decay, remember), so we have to run the formula for each year and sum them all; in Haskell:
sum $ map (\year -> ((1/500 * year ** (-(1.5))) + 1/30000) * 365.25) [1..20]
# 1.8291Which evaluates to 1.8 minutes. (This may seem too small, but one doesn’t spend much time in the first year and the time drops off quickly55.) Anki user muflax’s statistics put his per-card time at 71s, for example. But maybe Piotr Woźniak was being optimistic or we’re bad at writing flashcards, so we’ll double it to 5 minutes. That’s our key rule of thumb that lets us decide what to learn and what to forget: if, over your lifetime, you will spend more than 5 minutes looking something up or will lose more than 5 minutes as a result of not knowing something, then it’s worthwhile to memorize it with spaced repetition. 5 minutes is the line that divides trivia from useful data.56 (There might seem to be thousands of flashcards that meet the 5 minute rule. That’s fine. Spaced repetition can accommodate dozens of thousands of cards. See the next section.)
To a lesser extent, one might wonder when one is in a hurry, should one learn something with spaced repetition and with massed? How far away should the tests or deadlines be before abandoning spaced repetition? It’s hard to compare since one would need a specific regimens to compare for the crossover point, but for massed repetition, the average time after memorization at which one has a 50% chance of remembering the memorized item seems to be 3-5 days.57 Since there would be 2 or 3 repetitions in that period, presumably one would do better than 50% in recalling an item. 5 minutes and 5 days seems like a memorable enough rule of thumb: ‘don’t use spaced repetition if you need it sooner than 5 days or it’s worth less than 5 minutes’.
Overload
Spaced repetition is not infinite. Wozniak estimates a maximum number of ~300,000 items can be learned.
One common experience of new users to spaced repetition is to add too much stuff—trivialities and things they don’t really care about. But they soon learn the curse of Borges’s Funes the Memorious. If they don’t actually want to learn the material they put in, they will soon stop doing the daily reviews - which will cause reviews to pile up, which will be further discouraging, and so they stop. At least with physical fitness there isn’t a precisely dismaying number indicating how far behind you are! But if you have too little at the beginning, you’ll have few repetitions per day, and you’ll see little benefit from the technique itself - it looks like boring flash card review.
What to Add
I find one of the best uses for Mnemosyne is, besides the classic use of memorizing academic material such as geography or the periodic table or foreign vocabulary or Bible/Koran verses or the avalanche of medical school facts, to add in words from A Word A Day58 and Wiktionary, memorable quotes I see59, personal information such as birthdays (or license plates, a problem for me before), and so on. Quotidian uses, but all valuable to me. With a diversity of flashcards, I find my daily review interesting. I get all sorts of questions - now I’m trying to see whether a Haskell fragment is syntactically correct, now I’m pronouncing Korean hangul and listening to the answer, now I’m trying to find the Ukraine on a map, now I’m enjoying some A.E. Housman poetry, followed by a few quotes from LessWrong quote threads, and so on. Other people use it for many other things; one application that impresses me for its simple utility is memorizing names & faces of students although learning musical notes is also not bad.
The Workload
On average, when I’m studying a new topic, I’ll add 3–20 questions a day. Combined with my particular memory, I usually review about 90 or 100 items a day (out of the total >18,300). This takes under 20 minutes, which is not too bad. (I expect the time is expanded a bit by the fact that early on, my formatting guidelines were still being developed, and I hadn’t the full panoply of categories I do now - so every so often I must stop and edit categories.)
If I haven’t been studying something recently, the exponential decaying of reviews slowly drops the daily review. For example, in March 201115ya, I wasn’t studying many things, so for 2011-03-24–2011-03-2615ya, my scheduled daily reviews are 73, 83, and 74; after that, it will 201214ya, the daily reviews are in the 40s or sometimes 50s for similar reasons, but the gradual shrinkage will continue.
We can see this vividly, and we can even see a sort of analogue of the original forgetting curve, if we ask Mnemosyne 2.0 to graph the number of cards to review per day for the next year up to February 201313ya (assuming no additions or missed reviews etc.):
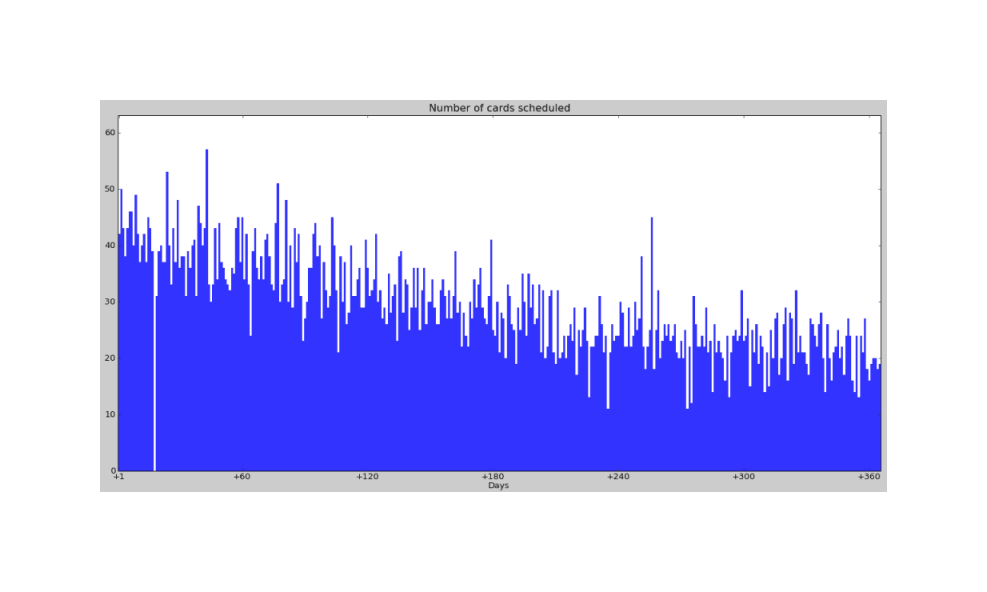
A wildly varying but clearly decreasing graph of predicted cards per day
If Mnemosyne weren’t using spaced repetition, it would be hard to keep up with 18,300+ flashcards. But because it is using spaced repetition, keeping up is easy.
Nor is 18.3k extraordinary. Many users have decks in the 6–7k range, Mnemosyne developer Peter Bienstman has >8.5k & Patrick Kenny >27k, Hugh Chen has a 73k+ deck, and in irc://irc.libera.chat#anki, they tell me of one user who triggered bugs with his >200k deck. 200,000 may be a bit much, but for regular humans, some amount smaller seems possible—it’s interesting to compare SRS decks to the feat of memorizing Paradise Lost or to the Muslim title of ‘hafiz’, one who has memorized the ~80,000 words of the Koran, or the stricter ‘hafid’, one who had memorized the Koran and 100,000 hadiths as well. Other forms of memory are still more powerful.60 (I suspect that spaced repetition is involved in one of the few well-documented cases of “hyperthymesia”, Jill Price: reading Wired, she has ordinary fallible powers of memorization for surprise demands with no observed anatomical differences and is restricted to “her own personal history and certain categories like television and airplane crashes”; further, she is a packrat with obsessive-compulsive traits who keeps >50,000 pages of detailed diaries—perhaps due to a childhood trauma—associates daily events nigh-involuntarily with past events. Marcus says the other instances of hyperthymesia resemble Price.)
When to Review
When should one review? In the morning? In the evening? Any old time? The studies demonstrating the spacing effect do not control or vary the time of day, so in one sense, the answer is: it doesn’t matter - if it did matter, there would be considerable variance in how effective the effect is based on when a particular study had its subjects do their reviews.
So one reviews at whatever time is convenient. Convenience makes one more likely to stick with it, and sticking with it overpowers any temporary improvement.
If one is not satisfied with that answer, then on general considerations, one ought to review before bedtime & sleep. Memory consolidation seems to be related, and sleep is known to powerfully influence what memories enter long-term memory, strengthening memories of material learned close to bedtime and increasing creativity; interrupting sleep without affecting total sleep time or quality still damages memory formation in mice61. So reviewing before bedtime would be best. (Other mental exercises show improvement when trained before bedtime; for example, dual n-back.) One possible mechanism is that it may be that the expectancy of future reviews/tests is enough to encourage memory consolidation during sleep; so if one reviews and goes to bed, presumably the expectancy is stronger than if one reviewed at breakfast and had an eventful day and forgot entirely about the reviewed flashcards. (See also the correlation between time of studying & GPA in 2012.) Neural growth may be related; from 2010:
Recent advances in our understanding of the neurobiology underlying normal human memory formation have revealed that learning is not an event, but rather a process that unfolds over time.16,17,18,[2003 Fundamental Neuroscience],20 Thus, it is not surprising that learning strategies that repeat materials over time enhance their retention.20,21,22,23,24,25,26
…Thousands of new cells are generated in this region every day, although many of these cells die within weeks of their creation.31 The survival of dentate gyrus neurons has been shown to be enhanced in animals when they are placed into learning situations.16-20 Animals that learn well retain more dentate gyrus neurons than do animals that do not learn well. Furthermore, 2 weeks after testing, animals trained in discrete spaced intervals over a period of time, rather than in a single presentation or a ‘massed trial’ of the same information, remember better.16-20 The precise mechanism that links neuronal survival with learning has not yet been identified. One theory is that the hippocampal neurons that preferentially survive are the ones that are somehow activated during the learning process.16-2062 The distribution of learning over a period of time may be more effective in encouraging neuronal survival by allowing more time for changes in gene expression and protein synthesis that extend the life of neurons that are engaged in the learning process.
…Transferring memory from the encoding stage, which occurs during alert wakefulness, into consolidation must thus occur at a time when interference from ongoing new memory formation is reduced.17,18 One such time for this transfer is during sleep, especially during non-rapid eye movement sleep, when the hippocampus can communicate with other brain areas without interference from new experiences.32,33,34 Maybe that is why some decisions are better made after a good night’s rest and also why pulling an all-nighter, studying with sleep deprivation, may allow you to pass an exam an hour later but not remember the material a day later.
Prospects: Extended Flashcards
Let’s step back for a moment. What are all our flashcards, small and large, doing for us? Why do I have a pair of flashcards for the word ‘anent’ among many others? I can just look it up.
But look ups take time compared to already knowing something. (Let’s ignore the previously discussed 5 minute rule.) If we think about this abstractly in a computer science context, we might recognize it as an old concept in algorithms & optimization discussions—the space-time tradeoff. We trade off lookup time against limited skull space.
Consider the sort of factual data already given as examples - we might one day need to know the average annual rainfall in Honolulu or Austin, but it would require too much space to memorize such data for all capitals. There are millions of English words, but in practice any more than 100,000 is excessive. More surprising is a sort of procedural knowledge. An extreme form of space-time tradeoffs in computers is when a computation is replaced by pre-calculated constants. We could take a math function and calculate its output for each possible input. Usually such a lookup table of input to output is really large. Think about how many entries would be in such a table for all possible integer multiplications between 1 and 1 billion. But sometimes the table is really small (like binary Boolean functions) or small (like trigonometric tables) or large but still useful (rainbow tables usually start in the gigabytes and easily reach terabytes).
Given an infinitely large lookup table, we could replace completely the skill of, say, addition or multiplication by the lookup table. No computation. The space-time tradeoff taken to the extreme of the space side of the continuum. (We could go the other way and define multiplication or addition as the slow computation which doesn’t know any specifics like the multiplication table - as if every time you wanted to add 2+2 you had to count on 4 fingers.)
So suppose we were children who wanted to learn multiplication. SRS and Mnemosyne can’t help because multiplication is not a specific factoid? The space-time tradeoff shows us that we can de-proceduralize multiplication and turn it partly into factoids. It wouldn’t be hard for us to write a quick script or macro to generate, say, 500 random cards which ask us to multiply AB by XY, and import them to Mnemosyne.63
After all, which is your mind going to do - get good at multiplying 2 numbers (generate on-demand), or memorize 500 different multiplication problems (memoize)? From my experience with multiple subtle variants on a card, the mind gives up after just a few and falls back on a problem-solving approach - which is exactly what one wants to exercise, in this case. Congratulations; you have done the impossible.
From a software engineering point of view, we might want to modify or improve the cards, and 500 snippets of text would be a tad hard to update. So coolest would be a ‘dynamic card’. Add a markup type like <eval src=""> , and then Mnemosyne feeds the src argument straight into the Python interpreter, which returns a tuple of the question text and the answer text. The question text is displayed to the user as usual, the user thinks, requests the answer, and grades himself. In Anki, Javascript is supported directly by the application in HTML <script> tags (currently inline only but Anki could presumably import libraries by default), for example for kinds of syntax highlighting, so any kind of dynamic card could be written that one wants.
So for multiplication, the dynamic card would get 2 random integers, print a question like x * y = ? and then print the result as the answer. Every so often you would get a new multiplication question, and as you get better at multiplication, you see it less often - exactly as you should. Still in a math vein, you could generate variants on formulas or programs where one version is the correct one and the others are subtly wrong; I do this by hand with my programming flashcards (especially if I make an error doing exercises, that signals a finer point to make several flashcards on), but it can be done automatically. kpreid describes one tool of his:
I have written a program (in the form of a web page) which does a specialized form of this [generating ‘damaged formulas’]. It has a set of generators of formulas and damaged formulas, and presents you with a list containing several formulas of the same type (eg. ∫ 2x dx = x^2 + C) but with one damaged (eg. ∫ 2x dx = 2x^2 + C).
This approach generalizes to anything you can generate random problems of or have large databases of examples of. Khan Academy apparently does something like this in associating large numbers of (algorithmicly-generated?) problems with each of its little modules and tracking retention of the skill in order to decide when to do further review of that module. For example, maybe you are studying Go and are interested in learning life-and-death positions. Those are things that can be generated by computer Go programs, or fetched from places like GoProblems.com. For even more examples, Go is rotationally invariant - the best move remains the same regardless of which way the board is oriented and since there is no canonical direction for the board (like in chess) a good player ought to be able to play the same no matter how the board looks - so each specific example can be mirrored in 3 other ways. Or one could test one’s ability to ‘read’ a board by writing a dynamic card which takes each example board/problem and adds some random pieces as long as some go-playing program like GNU Go says the best move hasn’t changed because of the added noise.
One could learn an awful lot of things this way. Programming languages could be learned this way - someone learning Haskell could take all the functions listed in the Prelude or his Haskell textbook, and ask QuickCheck to generate random arguments for the functions and ask the GHC interpreter ghci what the function and its arguments evaluate to. Games other than go, like chess, may work (a live example being Chess Tempo & Listudy, and see the experience of Dan Schmidt; or Super Smash Brothers). A fair bit of mathematics. If the dynamic card has Internet access, it can pull down fresh questions from an RSS feed or just a website; this functionality could be quite useful in a foreign language learning context with every day bringing a fresh sentence to translate or another exercise.
With some NLP software, one could write dynamic flashcards which test all sorts of things: if one confuses verbs, the program could take a template like “$PRONOUN $VERB $PARTICLE $OBJECT % {right: caresse, wrong: caresses}” which yields flashcards like “Je caresses le chat” or “Tu caresse le chat” and one would have to decide whether it was the correct conjugation. (The dynamicism here would help prevent memorizing specific sentences rather than the underlying conjugation.) In full generality, this would probably be difficult, but simpler approaches like templates may work well enough. Jack Kinsella:
I wish there were dynamic SRS decks for language learning (or other disciplines). Such decks would count the number of times you have reviewed an instance of an underlying grammatical rule or an instance of a particular piece of vocabulary, for example its singular/plural/third person conjugation/dative form. These sophisticated decks would present users with fresh example sentences on every review, thereby preventing users from remembering specific answers and compelling them to learn the process of applying the grammatical rule afresh. Moreover, these decks would keep users entertained through novelty and would present users with tacit learning opportunities through rotating vocabulary used in non-essential parts of the example sentence. Such a system, with multiple-level review rotation, would not only prevent against overfit learning, but also increase the total amount of knowledge learned per minute, an efficiency I’d gladly invest in.
Even though these things seem like ‘skills’ and not ‘data’!
Popularity
As of 2011-05-02:
Metric |
Mnemosyne |
iSRS |
|||
|---|---|---|---|---|---|
Homepage Alexa |
|||||
ML/forum members |
|||||
Ubuntu installs |
|||||
Debian installs |
|||||
Arch votes |
|||||
iPhone ratings |
Unreleased65 |
||||
Android ratings |
|||||
Android installs |
SuperMemo doesn’t fall under the same ratings, but it has sold in the hundreds of thousands over its 2 decades:
Biedalak is CEO of SuperMemo World, which sells and licenses Wozniak’s invention. Today, SuperMemo World employs just 25 people. The venture capital never came through, and the company never moved to California. About 50,000 copies of SuperMemo were sold in 200620ya, most for less than $50.84$302006. Many more are thought to have been pirated.66
It seems safe to estimate the combined market-share of Anki, Mnemosyne, iSRS and other SRS apps at somewhere under 50,000 users (making due allowance for users who install multiple times, those who install and abandon it, etc.). Relatively few users seem to have migrated from SuperMemo to those newer programs, so it seems fair to simply add that 50k to the other 50k and conclude that the worldwide population is somewhere around (but probably under) 100,000.
Where Was I Going With This?
Nowhere, really. Mnemosyne/SR software in general are just one of my favorite tools: it’s based on a famous effect67 discovered by science, and it exploits it elegantly68 and usefully. It’s a testament to the Enlightenment ideal of improving humanity through reason and overcoming our human flaws; the idea of SR is seductive in its mathematical rigor69. In this age where so often the ideal of ‘self-improvement’ and progress are decried, and gloom are espoused by even the common people, it’s really nice to just have a small example like this in one’s daily life, an example not yet so prosaic and boring as the lightbulb.
See Also
In the course of using Mnemosyne, I’ve written a number of scripts to generate repetitively varying cards.
mnemo.hswill take any newline-delimited chunk of text, like a poem, and generates every possible Cloze deletion; that is, an ABC poem will become 3 questions: _BC/ABC, A_C/ABC, AB_/ABCmnemo2.hsworks as above, but is more limited and is intended for long chunks of text wheremnemo.hswould cause a combinatorial explosion of generated questions; it generates a subset: for ABCD, one gets __CD/ABCD, A__D/ABCD, and AB__/ABCD (it removes 2 lines, and iterates through the list).mnemo3.hsis intended for date or name-based questions. It’ll take input like “Barack Obama is %47%.” and spit out some questions based on this: “Barack Obama is _7./47”, “Barack Obama is 4_./47” etc.mnemo4.hsis intended for long lists of items. If one wants to memorize the list of US Presidents, the natural questions for flashcards goes something like “Who was the 3rd president?/Thomas Jefferson”, “Thomas Jefferson was the _rd president./3”, “Who was president after John Adams?/Thomas Jefferson”, “Who was president before James Madison?/Thomas Jefferson”.You note there’s repetition if you do this for each president - one asks the ordinal position of the item both ways (item -> position, position -> item), what precedes it, and what succeeds it.
mnemo4.hsautomates this, given a list. In order to be general, the wording is a bit odd, but it’s better than writing it all out by hand! (Example output is in the comments to the source code).
The reader might well be curious by this point what my Mnemosyne database looks like. I use Mnemosyne quite a bit, and as of 2020-02-02, I have 16,149 (active) cards in my deck. Said curious reader may find my cards & media at gwern.cards (52M; Mnemosyne 2.x format).
The Mnemosyne project has been collecting user-submitted spaced repetition statistical data for years. The full dataset as of 2014-01-27 is available for download by anyone who wishes to analyze it.
External Links
Michael Nielsen: “Augmenting Long-term Memory”; “Quantum computing for the very curious”; “How can we develop transformative tools for thought?”
“A Year of Spaced Repetition Software in the Classroom”; two years; seven year followup; cf. “Easy Application of Spaced Practice in the Classroom”
AJATT table of contents -(applying SRS to learning Japanese)
Math:
“Using spaced repetition systems to see through a piece of mathematics”, Michael Nielsen
“Teaching linear algebra” (with spaced repetition), by Ben Tilly; Manual flashcards for his 2nd grader
Programming:
“Janki Method: Using spaced repetition systems to learn and retain technical knowledge” (Reddit discussion); SRS problems & solutions
“Memorizing a programming language using spaced repetition software” (Derek Sivers; HN)
“Chasing 10X: Leveraging A Poor Memory In Engineering”; “Everything I Know: Strategies, Tips, and Tricks for Anki”
“Remembering R—Using Spaced Repetition to finally write code fluently”
“QS Primer: Spaced Repetition and Learning” -(talks on applications of spaced repetition)
Value compared to curriculums:
Point: “Why Forgetting Can Be Good”, by Scott H. Young
Counterpoint: “Spaced repetition in natural and artificial learning”, by Ryan Muller
My own observation is that an optimally constructed curriculum could effectively implement spaced repetition, but even if it did (most don’t), unless it is computerized it will not adapt to the user.
Bash scripts for generating vocabulary flashcards (processing multiple online dictionaries, good for having multiple examples; images; and audio)
vocabulary selection:
“Diff revision: diff-based revision of text notes, using spaced repetition”
“A vote against spaced repetition”; “How Flashcards Fail: Confessions of a Tired Memory Guy”
“Learning Ancient Egyptian in an Hour Per Week with Beeminder”
“Using Anki with Babies / Toddlers”: 1, 2, 2, 4
followup at age 5 (cf. mutualism)
“SuperMemo does not work for kids”, Piotr Wozniak
SeRiouS: “Spaced Repetition Technology for Legal Education”, “SeRiouS: an LPTI-supported Project to Improve Students’ Learning and Bar Performance”, Gabe Teninbaum (video presentation)
“The role of digital flashcards in legal education: theory and potential”, et al 2014
“Making Summer Count: How Summer Programs Can Boost Children’s Learning”, et al 2011 (RAND MG1120)
“Factors that Influence Skill Decay And Retention: a Quantitative Review and Analysis”, et al 1998
“On The Forgetting Of College Academics: At ‘Ebbinghaus speed’?”, et al 2017
“Total recall: the people who never forget; An extremely rare condition may transform our understanding of memory” (obsessive recording & reviewing demonstrates you can recall much of your life if you live nothing worth recalling); “The Mystery of S., the Man with an Impossible Memory: The neuropsychologist Alexander Luria’s case study of Solomon Shereshevsky helped spark a myth about a man who could not forget. But the truth is more complicated”
Anki Essentials, Vermeer
“No. 126: Four Years of Spaced Repetition” (Gene Dan, actuarial studies)
“One Year Anki Update” (biology grad school)
“How To Remember Anything Forever-ish”: an interactive comic (Nicky Case)
“The Overfitted Brain: Dreams evolved to assist generalization”, 2020
“Relearn Faster and Retain Longer: Along With Practice, Sleep Makes Perfect”, et al 2016
“Replication and Analysis of Ebbinghaus’ Forgetting Curve”, 2015
“Learning from Errors”, 2017
Flashcard Sources
“One does not learn computing by using a hand calculator, but one can forget arithmetic.” —1982↩︎
Listing other neuroprosthetics is hard. It’s an interesting idea, but as proponents of externalism like Andy Clark have found, it’s easier to feel that externalism is meaningful than to nail down a clear definition which separates a neuroprosthetic or part of one’s mind from a random tool you like or find useful. Consider whether a pencil and paper a neuroprosthetic: clearly it is not for a child learning to write, who must carefully compose the words in his mind and put them down one after another, but it is not so clear for an adult who has been writing all his life and can doodle or write down thoughts without thinking about them and may even be surprised at what they happened to write.
I like this definition: “a neuroprosthetic is anything whose results you use without further thought”. So in the classic example, when Otto needs to go somewhere, he never thinks “I am an amnesiac who stores locations in my notepad, and I must look up the location” - he just looks up the location. A good heuristic would be anything whose destruction leaves one feeling lost, slow, stupid, or ignorant.
By this standard, I can think of only a few tools I use without noticeable thought:
keybindings such as window manager shortcuts, in particular shortcuts for Google searches; on occasion, XMonad’s Prompt gets inscrutably wedged, locking it. When this happens, I have to restart X because I Google everything and the keybinding is so engrained that not using it is unbearable. It would be like trying to write with your weak hand.
Google Calendar and PredictionBook: it is incredible how many followups or reminders or regularly happening tasks I can put into Google Calendar or PB. I have outsourced many habits or thoughts to them, and I no longer think of it as anything special. If either were gone, I would feel frightened - what events were passing, what beliefs falsified, what opportunities opening up (or closing!) that I had suddenly become ignorant of?
Evernote, for a similar reason; many of my memories have ceased to be things like “octopuses see too fast to watch TV and so only HDTV or UHDTV works for them; I read this in Orion Magazine” and become things like “octopus TV Evernote”, and if I want to know what it was about octopuses & TV, well, I’ll have to look it up in Evernote. Mnemosyne plays a similar role for me, but there the memories are much clearer on their own because of the spaced repetition.
my website Gwern.net; I’ve had to say many times that I don’t know what I think about something, but whatever that is, it’s on my website. (A more extreme form of the Evernote/Mnemosyne neuroprosthetic.) A commenter once wrote that reading Gwern.net felt like he was crawling around in my head. He was more right than he realized.
as quoted in “Retrieval practice and the maintenance of knowledge”, 1988↩︎
From “Close the Book. Recall. Write It Down: That old study method still works, researchers say. So why don’t professors preach it?”; The Chronicle of Higher Education
Two psychology journals have recently published papers showing that this strategy works, the latest findings from a decades-old body of research. When students study on their own, “active recall” - recitation, for instance, or flashcards and other self-quizzing - is the most effective way to inscribe something in long-term memory. Yet many college instructors are only dimly familiar with that research…
From “The Spacing Effect: A Case Study in the Failure to Apply the Results of Psychological Research” (1988), whose title alone summarizes the situation (see also 2007, Making Minds: What’s Wrong with Education - and What Should We Do About It?):
Second, it [the spacing effect] is remarkably robust. In many cases, two spaced presentations are about twice as effective as two massed presentations (eg. Hintzman, 197452ya; Melton, 1970), and the difference between them increases as the frequency of repetition increases (Underwood, 197056ya)…
The spacing effect was known as early as 1885141ya when Ebbinghaus published the results of his seminal work on memory. With himself as the subject, Ebbinghaus found that for a single 12-syllable series, 68 immediately successive repetitions had the effect of making possible an errorless recital after seven additional repetitions on the following day. However, the same effect was achieved by only 38 distributed repetitions spread over 3 days. On the basis of this and other related findings, Ebbinghaus concluded that ‘with any considerable number of repetitions a suitable distribution of them over a space of time is decidedly more advantageous than the massing of them at a single time’ (Ebbinghaus, 1885141ya/1913113ya. p. 89)
2012:
Furthermore, even after acknowledging the benefits of spacing, changing teaching practices proved to be enormously difficult. et al 2010 wrote: “Anecdotally, high school teachers and college professors seem to teach in a linear fashion without repetition and give three or four noncumulative exams.” (p. 130). Focusing on the math domain, where one might expect a very easy-to-review-and-to-space strategy, Rohrer (200917ya) points out that mathematics textbooks usually present topics in a non-spaced, non-mixed fashion. Even much earlier, Vash (198937ya) had written: “Education policy setters know perfectly well that [spaced practice] works better [than massed practice]. They don’t care. It isn’t tidy. It doesn’t let teachers teach a unit and dust off their hands quickly with a nice sense of ‘Well, that’s done.’” (p. 1547479ya).
Rohrer, D. (200917ya). “The effects of spacing and mixing practice problems”. Journal for Research in Mathematics Education, 40, 4-17
Vash, C. L. (198937ya). “The spacing effect: A case study in the failure to apply the results of psychological research”. American Psychologist, 44, 1547479ya (a comment on Dempster’s article?)
From Psychology: An Introduction:
↩︎In one practical demonstration of the spacing effect, Bahrick, Bahrick, Bahrick, & Bahrick (199333ya) showed that retention of foreign language vocabulary was greatly enhanced if practice sessions were spaced far apart. For example, “Thirteen retraining sessions spaced at 56 days yielded retention comparable to 26 sessions spaced at 14 days.” In other words, subjects could use half as many study sessions, if the study sessions were spread over a time period four times as long.
“Synaptic evidence for the efficacy of spaced learning”, et al 2012 (“Take your time: Neurobiology sheds light on the superiority of spaced versus massed learning”):
↩︎The superiority of spaced versus massed training is a fundamental feature of learning. Here, we describe unanticipated timing rules for the production of long-term potentiation (LTP) in adult rat hippocampal slices that can account for one temporal segment of the spaced trials phenomenon. Successive bouts of naturalistic theta burst stimulation of field CA1 afferents markedly enhanced previously saturated LTP if spaced apart by 1 h or longer, but were without effect when shorter intervals were used. Analyses of F-actin-enriched spines to identify potentiated synapses indicated that the added LTP obtained with delayed theta trains involved recruitment of synapses that were “missed” by the first stimulation bout. Single spine glutamate-uncaging experiments confirmed that less than half of the spines in adult hippocampus are primed to undergo plasticity under baseline conditions, suggesting that intrinsic variability among individual synapses imposes a repetitive presentation requirement for maximizing the percentage of potentiated connections. We propose that a combination of local diffusion from initially modified spines coupled with much later membrane insertion events dictate that the repetitions be widely spaced. Thus, the synaptic mechanisms described here provide a neurobiological explanation for one component of a poorly understood, ubiquitous aspect of learning.
There are many studies to the effect that active recall is best. Here’s one recent study, “Retrieval Practice Produces More Learning than Elaborative Studying with Concept Mapping”, 2011 (covered in Science Daily and the NYT):
Educators rely heavily on learning activities that encourage elaborative studying, while activities that require students to practice retrieving and reconstructing knowledge are used less frequently. Here, we show that practicing retrieval produces greater gains in meaningful learning than elaborative studying with concept mapping. The advantage of retrieval practice generalized across texts identical to those commonly found in science education. The advantage of retrieval practice was observed with test questions that assessed comprehension and required students to make inferences. The advantage of retrieval practice occurred even when the criterial test involved creating concept maps. Our findings support the theory that retrieval practice enhances learning by retrieval-specific mechanisms rather than by elaborative study processes. Retrieval practice is an effective tool to promote conceptual learning about science.
From “Forget What You Know About Good Study Habits”. New York Times;
↩︎Cognitive scientists do not deny that honest-to-goodness cramming can lead to a better grade on a given exam. But hurriedly jam-packing a brain is akin to speed-packing a cheap suitcase, as most students quickly learn - it holds its new load for a while, then most everything falls out….When the neural suitcase is packed carefully and gradually, it holds its contents for far, far longer. An hour of study tonight, an hour on the weekend, another session a week from now: such so-called spacing improves later recall, without requiring students to put in more overall study effort or pay more attention, dozens of studies have found.
“The idea is that forgetting is the friend of learning”, said Dr. Kornell. “When you forget something, it allows you to relearn, and do so effectively, the next time you see it.”
That’s one reason cognitive scientists see testing itself - or practice tests and quizzes - as a powerful tool of learning, rather than merely assessment. The process of retrieving an idea is not like pulling a book from a shelf; it seems to fundamentally alter the way the information is subsequently stored, making it far more accessible in the future.
In one of his own experiments, Dr. Roediger and Jeffrey Karpicke, who is now at Purdue University, had college students study science passages from a reading comprehension test, in short study periods. When students studied the same material twice, in back-to-back sessions, they did very well on a test given immediately afterward, then began to forget the material. But if they studied the passage just once and did a practice test in the second session, they did very well on one test two days later, and another given a week later.
The Mathematics of Gambling, 1984, §2 “The Wheels”, Chapter 4, pg43–44:
↩︎It was the spring of 195571ya. I was finishing my second year of graduate physics at U.C.L.A…I changed my field of study from physics to mathematics…I attended classes and studied 50–60 hours a week, generally including Saturdays and Sundays. I had read about the psychology of learning in order to be able to work longer and harder. I found that “spaced learning” worked well: study for an hour, then take a break of at least ten minutes (shower, meal, tea, errands, etc.). One Sunday afternoon about 3 p.m., I came to the co-op dining room for a tea break…My head was bubbling with physics equations, and several of my good friends were sitting around chatting.
From Final Jeopardy: Man Versus Machine and the Quest to Know Everything, by Stephen Baker, pg214:
↩︎The program he put together tested him on categories, gauged his strengths (sciences, NFL football) and weaknesses (fashion, Broadway shows), and then directed him toward the preparation most likely to pay off in his own match. To patch these holes in his knowledge, Craig used a free online tool called Anki, which provides electronic flash cards for hundreds of fields of study, from Japanese vocabulary to European monarchs. The program, in Craig’s words, is based on psychological research on ‘the forgetting curve’. It helps people find holes in their knowledge and determines how often they need those areas to be reviewed to keep them in mind. In going over world capitals, for example, the system learns quickly that a user like Craig knows London, Paris, and Rome, so it might spend more time reinforcing the capital of, say, Kazakhstan. (And what would be the Kazakh capital? ‘Astana’, Craig said in a flash. ‘It used to be Almaty, but they moved it.’)
“Our Interview With Jeopardy! Champion Arthur Chu”:
↩︎[Chu:] …Jeopardy! is aimed at the sort of average TV viewer, so they’re not going to ask things that are pointlessly obscure…So I used a program called Anki which uses a method called “spaced repetition.” It keeps track of where you’re doing well or poorly, and pushes you to study the flashcards you don’t know as well, until you develop an even knowledge base about a particular subject, and I just made flashcards for those specific things. I memorized all the world capitals, it wasn’t that hard once I had the flashcards and was using them every day. I memorized the US State Nicknames (they’re on Wikipedia), memorized the basic important facts about the 44 US Presidents. I really focused on those. But there’s a lot more stuff to know. I went on Jeopardy! knowing that there was stuff I didn’t know. For instance, everyone laughs about sports - but I also knew that [sports clues] were the least likely to come up in Double Jeopardy and Final Jeopardy and be very important. So I decided I shouldn’t sweat it too much, I should just recognize that I didn’t know them and let that go, as long as I can get the high value clues. So that was how I prepared.
Alan J. Perlis, “Epigrams in Programming” (198244ya)↩︎
Web developer Persol writes in August 2012:
↩︎I actually wrote a site that did this [spaced repetition] a few months ago. I had about 4000 users who had actually gone through a complete session…As guessed, the problem is that I couldn’t get people to start forming it as a habit. There is no immediate payback. Less than 20 people out of 4000 did more than one session…Additionally, there are at least 18 competitors. Here’s the list I made at the time. Very few seem to be successful. I shut the site down about a month ago. There are numerous free competitors which don’t have any great annoyances. I wouldn’t suggest starting another of these sites unless you figured out an effective way to “gamify” it.
…~4000 people finished a session. Many more ‘tried’ than 4000…I just couldn’t determine which users were bots that registered randomly vs users that didn’t finish the first session.
Tried: lots (but unknown)
Finished 1 session: ~4000
Finished >1 session: ~20 [0.5%]
“Play it Again: The Master Psychopharmacology Program as an Example of Interval Learning in Bite-Sized Portions”, et al 2010:
↩︎Since Ebbinghaus’ time, a voluminous amount of research has confirmed this simple but important fact: the retention of new information degrades rapidly unless it is reviewed in some manner. A modern example of this loss of knowledge without repetition is a study of cardiopulmonary resuscitation (CPR) skills that demonstrated rapid decay in the year following training. By 3 years post-training only 2.4% were able to perform CPR successfully.6 Another recent study of physicians taking a tutorial they rated as very good or excellent showed mean knowledge scores increasing from 50% before the tutorial to 76% immediately afterward.7 However, score gains were only half as great 3-8 days later and incredibly, there was no [statistically-]significant knowledge retention measurable at all at 55 days.7 Similar results have been reported by us in follow-up studies of knowledge retention from continuing medical education programs.1 [Stahl SM, Davis RL. Best Practices for Medical Educators. Carlsbad, CA: NEI Press; 200917ya]
…This may be due to the fact that lectures with assigned reading are the easiest for teachers. Also, medical learning is rarely measured immediately after a lecture or after reading new material for the first time and then measured again a few days or weeks later, so that the low retention rates of this approach may not be widely appreciated.1,4 No wonder formal medical education conferences without enabling or practice-reinforcing strategies appear to have relatively little impact on practice and healthcare outcomes.8,9,10
One study looking at cramming is the 199333ya “Cramming: A barrier to student success, a way to beat the system or an effective learning strategy?”, et al 1993, abstract:
Tested the hypothesis that cramming is an ineffective study strategy by examining the weekly study diaries of 166 undergraduates. All subjects also completed an end-of-semester questionnaire measuring study habits. subjects were classified in the following study patterns: ideal, confident, zealous, or crammer. Contrary to the hypothesis, results suggest that cramming is an effective approach, most widespread in courses using take-home essay examinations and major research papers. Crammers’ grades were as good as or better than those of subjects using other strategies; the longer subjects were in college, the more likely it was that they crammed. Crammers studied more hours than most students and were as interested in their courses as other students.
Note that there is no measure of long-term retention, suggesting that people who only care about grades are rationally choosing to cram.↩︎
Anki has its Cram Mode and Mnemosyne 2.0 has a cramming plugin. When a SRS doesn’t have explicit support, it’s always possible to ‘game’ the algorithm by setting one’s scores artificially low, so the SR algorithm thinks you are stupid and need to do a lot of repetitions.↩︎
“Examining the examiners: Why are we so bad at assessing students?”, 2002:
↩︎Conway, 1992 looked at long term memory for the information presented on a psychology course. They found that some types of information, especially that relating to research methods, were remembered better than others. But in a follow up analysis, they found that the type of assessment used had an effect on memory. In essence, material assessed by continuous assessment was more likely to be remembered than information assessed by exams.
2010:
↩︎For example, simple restudying allows the learner to reexperience all of the material but actually produces poor long-term retention.25,26,35 Why do students keep studying the original materials? Certainly if this is their only choice, then restudying is a necessary tactic. Another answer may be that repeated studying falsely inflates students’ confidence in their ability to remember in the future because they sense that they understand it now, and they and their instructors may be unaware of the many studies that show poor retention on delayed testing after this form of repetition.25,26,35
From et al 2010:
↩︎Contrary to the massing-aids-induction hypothesis, final test performance was consistently and considerably superior in the spaced condition. A large majority of participants, however, judged massing to be more effective than spacing, despite making the judgment after taking the test.
…Metacognitive judgments-that is, judgments about one’s own memory and cognition-are often based on feelings of fluency(eg. see Benjamin, Bjork, & Schwartz, 1998; Rhodes & Castel, 2008). Because massing naturally leads to feelings of fluency and increases short-term task performance during learning, learners frequently rate spacing as less effective than massing, even when their performance shows the opposite pattern (1978; Kornell & Bjork, 200818ya; Simon & Bjork, 200125ya; Zechmeister & Shaughnessy, 198046ya). Averaged across Kornell and Bjork’s (200818ya) experiments, for example, more than 80% of participants rated massing as equally or more effective than spacing, whereas only 15% of participants actually performed better in the massed condition than in the spaced condition.
…Such an illusion was apparent in the induction condition. Contrary to previous research, however, participants gave higher ratings for spacing than massing during repetition learning (see, eg. Simon & Bjork, 200125ya; Zechmeister & Shaughnessy, 198046ya). This outcome may have occurred because of a process of a habituation: Six presentations and a total of 30 s spent studying a single painting may have come to seem inefficient and pointless. Thus, there appears to be a turning point in metacognitive ratings based on fluency: As fluency increases, metacognitive ratings increase up to a point, but as fluency continues to increase and encoding or retrieval becomes too easy, metacognitive ratings may begin to decrease.
…In advance of their research, 2008 were convinced that such inductive learning would benefit from massing, yet their results showed the opposite. Undaunted, we remained convinced that spacing would be more beneficial for repetition learning than for inductive learning- especially for older adults, given their overall declines in episodic memory. The current results disconfirmed our expectations once again. If our intuitions are erroneous, despite our years spent proving and praising the spacing effect-including roughly 40 years’ worth contributed by Robert A. Bjork-those of the average student are surely mistaken as well (as the inaccuracy of the participants’ metacognitive ratings suggests). We have, perhaps, fallen victim to the illusion that making learning easy makes learning effective, rather than recognizing that spacing is a desirable difficulty (1994) that enhances inductive learning as well as repetition learning well into old age.
From 2012:
↩︎Thus, while spacing may boost learning, it may be thought to be relatively inefficient in terms of study time. As we discuss later, this feeling of inefficiency may be one of the reasons that spacing is not the more popular strategy. Interestingly, in that same study (1978; and see also 1985 and 1954 [Experimental Psychology]), there was evidence of such a thing as laboring in vain. That is, exceeding a certain number of hours of practice a day (more than approximately 2h) led to no increases in learning, as might be expected. Related to the deficient-processing theory mentioned above, these results are crucial in understanding intuitively how the spacing effect works: We simply get burnt out. These data are also analogous to the cognitive literature on overlearning, which shows that while continuous study over long periods of time might seem beneficial (and even feel good) in the short-term, the benefits disappear soon afterwards ( et al 2005; 2006)…In the above-described 1978’s study, for example, after postal workers practiced typing in either massed or spaced study sessions, they had to indicate how satisfied they were with the training. Results showed that while spacing led to the best learning, it was the least liked. Similarly, 2001 found that people preferred the massing strategy on a motor learning task.
Baddeley, A. D., & Longman, D. J. A. (197848ya). “The influence of length and frequency of training session on the rate of learning to type”. Ergonomics, 21, 627-635
Pirolli, P., & Anderson, J. R. (198541ya). “The role of practice in fact retrieval”
“Study strategies of college students: Are self-testing and scheduling related to achievement?”, 2012:
Previous studies, such as those by Kornell and Bjork (Psychonomic Bulletin & Review, 14:219-224, 200719ya) and Karpicke, Butler, and Roediger (Memory, 17:471-479, 200917ya), have surveyed college students’ use of various study strategies, including self-testing and rereading. These studies have documented that some students do use self-testing (but largely for monitoring memory) and rereading, but the researchers did not assess whether individual differences in strategy use were related to student achievement. Thus, we surveyed 324 undergraduates about their study habits as well as their college grade point average (GPA). Importantly, the survey included questions about self-testing, scheduling one’s study, and a checklist of strategies commonly used by students or recommended by cognitive research. Use of self-testing and rereading were both positively associated with GPA. Scheduling of study time was also an important factor: Low performers were more likely to engage in late-night studying than were high performers; massing (versus spacing) of study was associated with the use of fewer study strategies overall; and all students-but especially low performers-were driven by impending deadlines. Thus, self-testing, rereading, and scheduling of study play important roles in real-world student achievement.
(See also et al 2013.) Note the self-testing correlation excludes flashcards, a result that both the authors and me found surprising. The sleep connection is interesting, given the hypothesized link between stronger memory formation & studying before a good night’s sleep - you can hardly get a good night’s sleep if you are cramming late into the night (correlated with lower grades) but you can if you do so at a reasonable time in the evening (in time to get a solid night).
See also Susser & 2012:
↩︎Laboratory studies have demonstrated the long-term memory benefits of studying material in multiple distributed sessions as opposed to one massed session, given an identical amount of overall study time (ie. the spacing effect). The current study goes beyond the laboratory to investigate whether undergraduates know about the advantage of spaced study, to what extent they use it in their own studying, and what factors might influence its utilization. Results from a web-based survey indicated that participants (n = 285) were aware of the benefits of spaced study and would use a higher level of spacing under ideal compared to realistic circumstances. However, self-reported use of spacing was intermediate, similar to massing and several other study strategies, and ranked well below commonly used strategies such as rereading notes. Several factors were endorsed as important in the decision to distribute study time, including the perceived difficulty of an upcoming exam, the amount of material to learn, how heavily an exam is weighed in the course grade, and the value of the material. Further, level of metacognitive self-regulation and use of elaboration strategies were associated with higher rates of spaced study.
Analytic Culture in the US Intelligence Community: An Ethnographic Study, 2005, pg89:
To investigate the intensity of instructional interactions, Art Graesser and Natalie 1994 compared questioning and answering in classrooms with those in tutorial settings.5 They found that classroom groups of students ask about three questions an hour and that any single student in a classroom asks about 0.11 questions per hour. In contrast, they found that students in individual tutorial sessions asked 20-30 questions an hour and were required to answer 117-146 questions per hour. Reviews of the intensity of interaction that occurs in technology-based instruction have found even more active student response levels. [J. D. Fletcher, Technology, the Columbus Effect, and the Third Revolution in Learning.]
Although 1994 also found that sheer number of questions was not necessarily important, suggesting diminishing marginal returns or perhaps bad question asking.↩︎
“SuperMemo is based on the insight that there is an ideal moment to practice what you’ve learned. Practice too soon and you waste your time. Practice too late and you’ve forgotten the material and have to relearn it. The right time to practice is just at the moment you’re about to forget. Unfortunately, this moment is different for every person and each bit of information. Imagine a pile of thousands of flash cards. Somewhere in this pile are the ones you should be practicing right now. Which are they?” Gary Wolf, “Want to Remember Everything You’ll Ever Learn? Surrender to This Algorithm”, Wired Magazine↩︎
“Make no mistake about it: Computers process numbers - not symbols. We measure our understanding (and control) by the extent to which we can arithmetize an activity.” Perlis, ibid.↩︎
this exponential expansion is how a SR program can handle continual input of cards: if cards were scheduled at fixed intervals, like every other day, review would soon become quite impossible - I have >18000 items in Mnemosyne, but I don’t have time to review 9000 questions a day!↩︎
See the 200818ya meta-analysis, “Learning Styles: Concepts and Evidence” (APS press release); from the abstract:
↩︎…in order to demonstrate that optimal learning requires that students receive instruction tailored to their putative learning style, the experiment must reveal a specific type of interaction between learning style and instructional method: Students with one learning style achieve the best educational outcome when given an instructional method that differs from the instructional method producing the best outcome for students with a different learning style. In other words, the instructional method that proves most effective for students with one learning style is not the most effective method for students with a different learning style.
Our review of the literature disclosed ample evidence that children and adults will, if asked, express preferences about how they prefer information to be presented to them. There is also plentiful evidence arguing that people differ in the degree to which they have some fairly specific aptitudes for different kinds of thinking and for processing different types of information. However, we found virtually no evidence for the interaction pattern mentioned above, which was judged to be a precondition for validating the educational applications of learning styles. Although the literature on learning styles is enormous, very few studies have even used an experimental methodology capable of testing the validity of learning styles applied to education. Moreover, of those that did use an appropriate method, several found results that flatly contradict the popular meshing hypothesis.
We conclude therefore, that at present, there is no adequate evidence base to justify incorporating learning-styles assessments into general educational practice. Thus, limited education resources would better be devoted to adopting other educational practices that have a strong evidence base, of which there are an increasing number. However, given the lack of methodologically sound studies of learning styles, it would be an error to conclude that all possible versions of learning styles have been tested and found wanting; many have simply not been tested at all.
Fritz, C. O., Morris, P. E., Acton, M., Etkind, R., & Voelkel, A. R (200719ya). “Comparing and combining expanding retrieval practice and the keyword mnemonic for foreign vocabulary learning”. Applied Cognitive Psychology, 21, 499-526.↩︎
From et al 2007, describing 1939, “Studies in retention”:
↩︎Spitzer (193987ya) incorporated a form of expanded retrieval in a study designed to assess the ability of sixth graders to learn science facts. Impressively, Spitzer tested over 3600 students in Iowa-the entire sixth-grade population of 91 elementary schools at the time. The students read two articles, one on peanuts and the other on bamboo, and were given a 25-item multiple choice test to assess their knowledge (such as ‘To which family of plants does bamboo belong?’). Spitzer tested a total of nine groups, manipulating both the timing of the test (administered immediately or after various delays) and the number of identical tests students received (one to three). Spitzer did not incorporate massed or equal interval retrieval conditions, but he had at least two groups that were tested on an expanding schedule of retrieval, in which the intervals between tests were separated by the passage of time (in days) rather than by intervening to-be-learned information. For example, in one of the groups, the first test was given immediately, the second test was given seven days after the first test, and the third test was given 63 days after the second test. Thus, in essence, this group was tested on a 0-7-63 day expanding retrieval schedule. Spitzer compared performance of the expanded retrieval group to a group given a single test 63 days after reading the original article. On the first (immediate) test, the expanded retrieval group correctly answered 53% of the questions. After 63 days and two previous tests, their score was still an impressive 43%. The single test group correctly answered only 25% of the original items after 63 days, giving the expanded retrieval group an 18% retention advantage. This is quite impressive, given that this large benefit remained after a 63-day retention interval. Similar beneficial effects were found in a group tested on a 0-1-21 day expanded retrieval schedule compared to a group given a single test after 21 days. Of course, this study does not decouple the effects of testing from spacing or expansion, but the results do clearly indicate considerable learning and retention using the expanded repeated testing procedure. Spitzer concluded that ‘…examinations are learning devices and should not be considered only as tools for measuring achievement of pupils’ (p. 656, italics added)
-
↩︎The spacing effect describes the robust finding that long-term learning is promoted when learning events are spaced out in time, rather than presented in immediate succession. Studies of the spacing effect have focused on memory processes rather than for other types of learning, such as the acquisition and generalization of new concepts. In this study, early elementary school children (5-7 year-olds; N = 36) were presented with science lessons on one of three schedules: massed, clumped, and spaced. The results revealed that spacing lessons out in time resulted in higher generalization performance for both simple and complex concepts. Spaced learning schedules promote several types of learning, strengthening the implications of the spacing effect for educational practices and curriculum.
See also 2006, who compared spacing & massed in an introductory psychology course as well.↩︎
2006b again.↩︎
et al 2007 review:
No feedback or correction was given to subjects if they made errors or omitted answers. 1978 found that the expanding-interval schedule produced better recall than equal-interval testing on a final test at the end of the session, and equal-interval testing, in turn, produced better recall than did initial massed testing. Thus, despite the fact that massed testing produced nearly errorless performance during the acquisition phase, the other two schedules produced better retention on the final test given at the end of the session. However, the difference favoring the expanding retrieval schedule over the equal-interval schedule was fairly small at around 10%. In research following up Landauer and Bjork’s (197848ya) original experiments, practically all studies have found that spaced schedules of retrieval (whether equal-interval or expanding schedules) produce better retention on a final test given later than do massed retrieval tests given immediately after presentation (eg. Cull, 200026ya; Cull, Shaughnessy, & Zechmeister, 199630ya), although exceptions do exist. For example, in Experiments 3 and 4 of et al 1996, massed testing produced performance as good as equal-interval testing on a 5-5-5 schedule, but most other experiments have found that any spaced schedule of testing (either equal-interval or expanding) is better than a massed schedule for performance on a delayed test. However, whether expanding schedules are better than equal-interval schedules for long-term retention-the other part of Landauer and Bjork’s interesting findings-remains an open question. Balota, Duchek, and Logan (in press) have provided a thorough consideration of the relevant evidence and have shown that it is mixed at best, and that most researchers have found no difference between the two schedules of testing. That is, performance on a final test at the end of a session often shows no difference in performance between equal-interval and expanding retrieval schedules.
Cull, for those curious (Cull, W. L. (200026ya). “Untangling the benefits of multiple study opportunities and repeated testing for cued recall”. Applied Cognitive Psychology, 14, 215-235):
↩︎Cull (200026ya) compared expanded retrieval to equal interval spaced retrieval in a series of four experiments designed to mimic typical teaching or study strategies encountered by students. He examined the role of testing versus simply restudying the material, feedback, and various retention intervals on final test performance. Paired associates (an uncommon word paired with a common word, such as bairn-print) were presented in a manner similar to the flashcard techniques students often use to learn vocabulary words. The intervals between retrieval attempts of to-be-learned information ranged from minutes in some experiments to days in others. Interestingly, across four experiments, Cull did not find any evidence of an advantage of an expanded condition over a uniform spaced condition (ie. no [substantial] expanded retrieval effect), although both conditions consistently produced large advantages over massed presentations. He concluded that distributed testing of any kind, expanded or equal interval, can be an effective learning aid for teachers to provide for their students.
The et al 2007 review offers a synthesis of current theories on how massed and spaced differ, based on memory encoding:
According to encoding variability theory, performance on a memory test is dependent upon the overlap between the contextual information available at the time of test and the contextual information available during encoding. During massed study, there is relatively little time for contextual elements to fluctuate between presentations and so this condition produces the highest performance in an immediate memory test, when the test context strongly overlaps with the same contextual information encoded during both of the massed presentations. In contrast, when there is spacing between the items, there is time for fluctuation to take place between the presentations during study, and hence there is an increased likelihood of having multiple unique contexts encoded. Because a delayed test will also allow fluctuation of context, it is better to have multiple unique contexts encoded, as in the spaced presentation format, as opposed to a single encoded context, as in the massed presentation format.
et al 2010 did 3 experiments on reading comprehension:
↩︎On a test 1 week later, recall was enhanced by the expanding schedule, but only when the task between successive retrievals was highly interfering with memory for the passage. These results suggest that the extent to which learners benefit from expanding retrieval practice depends on the degree to which the to-be-learned information is vulnerable to forgetting.
From Mnemosyne’s Principles page:
↩︎The Mnemosyne algorithm is very similar to SM2 used in one of the early versions of SuperMemo. There are some modifications that deal with early and late repetitions, and also to add a small, healthy dose of randomness to the intervals. Supermemo now uses SM11. However, we are a bit skeptical that the huge complexity of the newer SM algorithms provides for a statistically relevant benefit. But, that is one of the facts we hope to find out with our data collection. We will only make modifications to our algorithms based on common sense or if the data tells us that there is a statistically relevant reason to do so.
et al 2007:
↩︎Carpenter and DeLosh (200521ya, Exp. 2) have recently investigated face-name learning under massed, expanded (1-3-5), and equal interval (3-3-3) conditions. This study also involved study and study and test procedures during the acquisition phase. Carpenter and DeLosh found a large effect of spacing, but no evidence of a benefit of expanded over equal interval practice. In fact, Carpenter and DeLosh reported a reliable benefit of the equal interval condition over the expanded retrieval condition.
et al 2007 again:
↩︎1985 tested the effectiveness of expanded retrieval in a third-grade classroom setting. In separate conditions, students were given new multiplication problems or spelling words to learn. The problem or word was presented audiovisually once and then tested on either a massed retrieval schedule of 0-0-0-0 or an expanding schedule of 0-1-2-4, in which the intervals involved being tested on old items or learning new items. After each test trial for a given item, the item was re-presented in its entirety so students received feedback on what they were learning. Performance during the learning phase was at 100% for both spelling words and multiplication facts. On an immediate final retention test, Rea and Modigliani found a performance advantage for all items-math and spelling- practiced on an expanding schedule compared to the massed retrieval schedule. They suggested, as have others, that spacing combined with the high success rate inherent in the expanded retrieval schedule produced better retention than massed retrieval practice. However, as in Spitzer’s study, Rea and Modigliani did not test an appropriate equal interval spacing condition. Hence, their finding that expanded retrieval is superior to massed retrieval in third graders could simply reflect the superiority of spaced versus massed rehearsal-in other words, the spacing effect.
et al 2007; >1 is rare in psychology, see “One Hundred Years of Social Psychology Quantitatively Described”, et al 2003↩︎
2006↩︎
et al 2007:
↩︎…long-term retention of information has been demonstrated over several days in some cases (eg. Camp et al, 199630ya). For example, in the latter study, Camp et al employed an expanding retrieval strategy to train 23 individuals with mild to moderate AD to refer to a daily calendar as a cue to remember to perform various personal activities (eg. take medication). Following a baseline phase to determine whether subjects would spontaneously use the calendar, spaced retrieval training was implemented by repeatedly asking the subject the question, ‘How are you going to remember what to do each day?’ at expanding time intervals. The results indicated that 20/23 subjects did learn the strategy (ie. to look at the calendar) and retained it over a 1-week period.
2006 warns us, though, about many of the other math studies:
↩︎In one meta-analysis by 1999, for instance, the size of the spacing effect declined sharply as conceptual difficulty of the task increased from low (eg. rotary pursuit) to average (eg. word list recall) to high (eg. puzzle). By this finding, the benefits of spaced practise may be muted for many mathematics tasks.
What is especially nice about this study was that not only did it use high-quality (intelligent & motivated) college students (United States Air Force Academy), the conditions were relatively controlled - both groups had the same homework (so equal testing effect), but like 2006/2007, the distribution was what varied:
↩︎The course topics, textbook, handouts, reading assignments, and graded assignments (with the exception of quiz, homework, and participation points) were identical for the treatment and control groups. The listing of homework assignments in the syllabus differed between groups. The control group was assigned daily homework related to the topic(s) presented that day in class. Peterson (197155ya) calls this the vertical model for assigning mathematics homework. The treatment group was assigned homework in accordance with a distributed organizational pattern that combines practice on current topics and reinforcement of previously covered topics. Under the distributed model, approximately 40% of the problems on a given topic were assigned the day the topic was first introduced, with an additional 20% assigned on the next lesson and the remaining 40% of problems on the topic assigned on subsequent lessons (Hirsch et al, 198343ya). In Hirsch’s research and in this study, after the initial homework assignment, problem(s) representing a given topic resurfaced on the 2nd, 4th, 7th, 12th, and 21st lesson. Consequently, treatment group homework for lesson one consisted of only one topic; homework for lessons two and three consisted of two topics; and homework for lesson four through six consisted of three topics. This pattern continued as new topics were added and was applied to all non-exam, non-laboratory lessons. As shown by Tables 1 and 2, the same homework problems were assigned to both groups with only the pattern of assignment differing. Because of the nature of the distributed practice model, homework for the treatment group contained fewer problems (relative to the control group) early in the semester with the number of problems increasing as the semester progressed. Later in the semester, homework for the treatment group contained more problems (relative to the control group)….The USAFA routinely collects study time data. After each exam, a large sample of cadets (at least 60% of the course population) anonymously reported the amount of time (in minutes) spent studying for the exam. Time spent studying was approximately equal for both groups (see Table 5). Descriptive data revels that, for both the treatment and control group, study time for the third exam was at least 16% greater than study time for any other exam. Study time for the final exam was at least 68% greater than study time for any of the hourly exams (see Table 5)
…The treatment produced an effect size (f 2) of 0.013 on the first exam, 0.029 on the second exam, 0.035 on the fourth exam, and 0.040 on the final course percentage grade. Although the effect sizes appear to be small, the treatment group outscored the control group in every case. A mean difference of 5.13 percentage points on the first, second, and fourth exam translates to an advantage of about a third of a letter grade for students in the treatment group. In addition, higher minimum scores earned by the treatment group may indicate that the distributed practice treatment served to eliminate the extremely low scores (refer to Table 3)….Oddly, the distributed practice treatment did not produce a [statistically-]significant effect on final exam scores. One possible cause for the disparity was the USAFA policy exempting the top performers from the final exam. Of the 16 exempted students, 11 were from the treatment group with only 5 from the control group.
2006 abstract:
↩︎Two introductory psychology classes (N = 145) participated in a counterbalanced classroom experiment that demonstrated the spacing effect and, by analogy, the benefits of distributed study. After hearing words presented twice in either a massed or distributed manner, participants recalled the words and scored their recall protocols, reliably remembering more distributed than massed words. Posttest scores on a multiple-choice quiz covering points illustrated by the experiment averaged about twice the comparable pretest scores, indicating the effectiveness of the exercise in conveying content. Students’ subjective ratings suggested that the experiment helped convince them of the benefits of distributed study.
See et al 2006↩︎
Commins, S., Cunningham, L., Harvey, D., and Walsh, D. (200323ya). “Massed but not spaced training impairs spatial memory”. Behavioural Brain Research 139, 215-223↩︎
Galluccio & Rovee-2006, “Nonuniform effects of reinstatement within the time window”. Learning and Motivation, 37, 1-17.↩︎
See the previous sections for many using children; one previously uncited is 1993, “The spacing effect in preschool children’s free recall of pictures and words”; but et al 2009 adds some interesting qualifiers to spaced repetition in the young:
↩︎Preschoolers, elementary school children, and college students exhibited a spacing effect in the free recall of pictures when learning was intentional. When learning was incidental and a shallow processing task requiring little semantic processing was used during list presentation, young adults still exhibited a spacing effect, but children consistently failed to do so. Children, however, did manifest a spacing effect in incidental learning when an elaborate semantic processing task was used.
Another previously uncited study: Glenberg, A. M. (197947ya), “Component-levels theory of the effects of spacing of repetitions on recall and recognition”. Memory & Cognition, 7, 95-112.↩︎
See et al 2010; et al 2012 shows the spacing benefits but reduced in magnitude in its 56-74 year old subjects, similar to et al 2012 and 2013↩︎
Mammarella, N., Russo, R., & Avons, S. E. (200224ya). ”Spacing effects in cued-memory tasks for unfamiliar faces and nonwords”. Memory & Cognition, 30, 1238–1251↩︎
Childers, J. B., & Tomasello, M. (200224ya). ”Two-year-olds learn novel nouns, verbs, and conventional actions from massed or distributed exposures”. Developmental Psychology, 38, 967-978↩︎
eg. et al 1968↩︎
The famous ‘10,000 hours of practice’ figure may not be as true or important as Ericsson and publicizers like Malcolm Gladwell imply, given the high variance of expertise against time, and results from sports showing smaller time investments (see also Hambrick’s corpus cutting ‘deliberate practice’ down to size), and Ericsson absurdly deny the powerful role of genetics and the necessary condition of having talent but the insight of ‘deliberate practice’ helping talented people probably is real. One may be able to get away with 3,000 hours rather than 10,000, but one isn’t going to do that with mindless repetition or no repetitions.↩︎
Gentner, D., Loewenstein, J., & Thompson, L. (200323ya). “Learning and transfer: A general role for analogical encoding”. Journal of Educational Psychology, 95, 393-40↩︎
From et al 2010:
↩︎The benefits of spacing seem to diminish or disappear when to-be-learned items are not repeated exactly (Appleton-Knapp, Bjork, & Wickens, 2005)…a number of studies have shown that massing, rather than spacing, promotes inductive learning. These studies have generally employed relatively simple perceptual stimuli that facilitate experimental control (Gagné, 1950; Goldstone, 1996; Kurtz & Hovland, 1956; [Whitman J. R., & Garner, W. R. (196363ya). “Concept learning as a function of the form of internal structure”. Journal of Verbal Learning & Verbal Behavior, 2, 195-202]).
High error rates - indicating one didn’t actually learn the card contents in the first place - seem to be connected to failures of the spacing effect; there’s some evidence that people naturally choose to mass study when they don’t yet know the material.↩︎
The 20 years look like this (note the scientific notation):
[0.742675, 0.27044575182838654, 0.15275979054767388, 0.10348750000000001, 7.751290630254386e-2, 6.187922936397532e-2, 5.161829250474865e-2, 4.445884397854832e-2, 3.923055555555555e-2, 3.5275438307530015e-2, 3.219809429218694e-2, 2.9748098818459235e-2, 2.7759942051635768e-2, 2.6120309801216147e-2, 2.474928593068675e-2, 2.35890625e-2, 2.2596898475825956e-2, 2.1740583401051353e-2, 2.0995431241707652e-2, 2.0342238287817983e-2]↩︎modulo things where knowing it is useful even if you don’t need it often - it can be a brick in a pyramid of knowledge; cf. page 3 of Wolf:
↩︎The problem of forgetting might not torment us so much if we could only convince ourselves that remembering isn’t important. Perhaps the things we learn - words, dates, formulas, historical and biographical details - don’t really matter. Facts can be looked up. That’s what the Internet is for. When it comes to learning, what really matters is how things fit together. We master the stories, the schemas, the frameworks, the paradigms; we rehearse the lingo; we swim in the episteme.
The disadvantage of this comforting notion is that it’s false. “The people who criticize memorization - how happy would they be to spell out every letter of every word they read?” asks Robert Bjork, chair of UCLA’s psychology department and one of the most eminent memory researchers. After all, Bjork notes, children learn to read whole words through intense practice, and every time we enter a new field we become children again. “You can’t escape memorization,” he says. “There is an initial process of learning the names of things. That’s a stage we all go through. It’s all the more important to go through it rapidly.” The human brain is a marvel of associative processing, but in order to make associations, data must be loaded into memory.
See Stephen R. Schmidt’s webpage “Theories of Forgetting”, which cites ‘Woodworth & Schlosbeg (196165ya)’ when presenting a log graph of various studies’ forgetting curves.↩︎
which neatly addresses the issue of such mailing lists being useless (‘who learns a word after just one exposure?’).↩︎
Mnemosyne in this case constitutes both a way to learn the quotes so I can use them, and a waste book; just the other day I had 3 or 4 apposite quotes for an essay because I had entered them into Mnemosyne months or years ago.↩︎
It’s well known that any speaker of a language understands many more words than they will ever use or be able to explicitly generate, that their “reading vocabulary” exceeds their “writing vocabulary”; less well-known is that on many problems, one can guess at well above random rates even while feeling unsure & ignorant, necessitating psychologists to employ forced-choice paradigms to reveal such “dark knowledge”. Even less known is the capacity of recognition memory or “implicit memory” (cf. McCollough effect); this memory can apply to things like recognizing images or text or music, typing, puzzle solving, etc. Andrew Drucker, in “Multiplying 10-digit numbers using Flickr: The power of recognition memory”, employs visual memory to calculate 9,883,603,368 × 4,288,997,768 = 42,390,752,785,149,282,624; he cites as precedent 1973:
In one of the most widely-cited studies on recognition memory, Standing showed participants an epic 10,000 photographs over the course of 5 days, with 5 seconds’ exposure per image. He then tested their familiarity, essentially as described above. The participants showed an 83% success rate, suggesting that they had become familiar with about 6,600 images during their ordeal. Other volunteers, trained on a smaller collection of 1,000 images selected for vividness, had a 94% success rate.
One sometimes sees people argue that something is insecure or unguessable or free from possible placebo effect because it involves too many objects to explicitly memorize, but as these examples make clear, recognition memory can happen quickly and store surprisingly large amounts of information. This could be used for authentication (see for example et al 2012; HN discussion) or message since recognition memory could be exploited as a sort of secure communication system. Two parties can share a set of 20,000 photographs (10,000 pairs); to send a message, have a messenger spend 5 days on 10,000 picked ones; and then to receive it, ask him to recognize which photograph he saw in each of the 10,000 pairs. The subject not only does not know what the binary message is or what means, he can’t even produce it since he cannot remember the photographs!
At an 80% accuracy rate, we can even calculate how many bits of information can be entrusted to the messenger using Shannon’s theorem; a calculation gives 5.8 kilobits as the upper limit: if p = 0.2 (based on the 80% success rate), then 10000 / (1 − (p × log2 p + (1 − p) × (log2 (1 − p)))) = 5,807.44. (This message can, of course, be encrypted.)
So we see that Frank Herbert was right after all: the securest way to send a message is through a “distrans” messenger! (The downside is that the implicit recognition memory decays; see 1986 for adjusted estimates.)
This system is even more interesting because the learning happens unconsciously, without volition, so the subject does not need to cooperate nor even know about it (they could be exposed to key images without realizing it, such as through ‘advertising’). Further, recognition of an image also happens unconsciously, and can be observed by EEG ERPs & fMRI (and probably other neural correlates or modalities like eyetracking or skin galvanic response). Thus, messages can be stored & retrieved both unconsciously & involuntarily in brains!↩︎
In this vein, I am reminded of what a former polyphasic sleeper told me:
↩︎I’ve been polyphasic for about a year. (Not anymore; kills my memory.)…Anki reps, mostly. I found that I could do proper review sessions for about 2–3 days and would hit an impenetrable wall. I couldn’t learn a single new card and had total brain fog until I got 3 hours more sleep. That, however, would reset my adaptation. The whole effect is a bit less pronounced on Everyman, but not much. It is however easier to add sleep when you already have a core. I didn’t notice any other major mental impairment after the initial sleep deprivation.
For a more recent review, see et al 2013.↩︎
Presumably one would immediately give them all some high grade like 5 to avoid suddenly having a daily load of 500 cards for a while.↩︎
Smaller is better.↩︎
“For Mnemosyne 2.x, Ullrich is working on an official Mnemosyne iPhone client which will have very easy syncing.”↩︎
See Page 4, 2008:
↩︎The spacing effect was one of the proudest lab-derived discoveries, and it was interesting precisely because it was not obvious, even to professional teachers. The same year that Neisser revolted, Robert Bjork, working with Thomas Landauer of Bell Labs, published the results of two experiments involving nearly 700 undergraduate students. Landauer and Bjork were looking for the optimal moment to rehearse something so that it would later be remembered. Their results were impressive: The best time to study something is at the moment you are about to forget it. And yet - as Neisser might have predicted - that insight was useless in the real world.
When I first read of SuperMemo, I had already taken a class in cognitive psychology and was reasonably familiar with Ebbinghaus’s forgetting curve - so my reaction to its methodology was Huxley’s: “How extremely stupid not to have thought of that!”↩︎
See page 7, 2008
↩︎And yet now, as I grin broadly and wave to the gawkers, it occurs to me that the cold rationality of his approach may be only a surface feature and that, when linked to genuine rewards, even the chilliest of systems can have a certain visceral appeal. By projecting the achievement of extreme memory back along the forgetting curve, by provably linking the distant future - when we will know so much - to the few minutes we devote to studying today, Wozniak has found a way to condition his temperament along with his memory. He is making the future noticeable. He is trying not just to learn many things but to warm the process of learning itself with a draft of utopian ecstasy.