---
title: When Should I Check The Mail?
description: "Bayesian decision-theoretic analysis of local mail delivery times: modeling deliveries as survival analysis, model comparison, optimizing check times with a loss function, and optimal data collection."
created: 2015-06-21
modified: 2018-02-24
status: finished
previous: /milk
next: /candy-japan
confidence: highly likely
importance: 8
css-extension: dropcaps-yinit
...
> Mail is delivered by the USPS mailman at a regular but not observed time; what is observed is whether the mail has been delivered at a time, yielding somewhat-unusual "interval-censored data".
> I describe the problem of estimating when the mailman delivers, write a simulation of the data-generating process, and demonstrate analysis of interval-censored data in R using maximum-likelihood (survival analysis with Gaussian regression using `survival` library), MCMC (Bayesian model in JAGS), and likelihood-free Bayesian inference (custom ABC, using the simulation). This allows estimation of the distribution of mail delivery times.
> I compare those estimates from the interval-censored data with estimates from a (smaller) set of exact delivery-times provided by USPS tracking & personal observation, using a multilevel model to deal with heterogeneity apparently due to a change in USPS routes/postmen.
> Finally, I define a loss function on mail checks, enabling: a choice of optimal time to check the mailbox to minimize loss (exploitation); optimal time to check to maximize information gain (exploration); Thompson sampling (balancing exploration & exploitation indefinitely), and estimates of the value-of-information of another datapoint (to estimate when to stop exploration and start exploitation after a finite amount of data).
Consider a question of burning importance: what time does the mailman come, bearing gifts and when should I check my mail---considering that my mailbox is >110m/>7.5 minutes away, and that I *really* dislike walking out to it in up to 90F heat for a package or book only to discover the mail hasn't come yet?
No one wants to sit around all morning to spot the *exact* time the mailman comes. At least, I don't.
We could more easily measure by going out in the morning at a random time to see if the mail has come yet, and then (somehow) estimate.
Given a set of data like "2015-06-20 11:00AM: mail has not come yet; 2015-06-21 11:59AM: mail had come", how can we estimate?
This is not a normal setup where we estimate a mean but our data is interestingly messed up: censored or truncated or an interval somehow.
[Survival analysis](!W) seems like the appropriate paradigm.
This is not a simple survival analysis with "right-censoring" where each individual is followed up to a censoring time and the exact time of 'failure' is observed.
(This would be right-censoring if instead we had gone out to the mailbox early in the morning and sat there waiting for the mailman to record when she came, occasionally getting bored around 10AM or 11AM and wandering off without seeing when the mail comes.)
This isn't "left-censoring" either (for left-censoring, we'd go out to the mailbox late in the morning when the mail might already be there, and if it isn't, then wait until it does come).
I don't think this is left or right truncation either, since each day data is collected and there's no sampling biases at play.
What this is, is interval censoring: when we go out to the mailbox at 11AM and discover the mail is there, we learn that the mail was delivered today sometime in the interval midnight-10:59AM, or if the mail isn't there, we learn it will be delivered later today sometime during the interval 11:01AM-midnight (hopefully closer to the first end than the second).
Interval censoring comes up in biostatistics for situations like periodic checkups for cancer, which does resemble our mail situation.
# Inference
## Interval-censored data
### ML
The R [`survival` library](https://cran.r-project.org/web/packages/survival/index.html) supports the usual right/left-censoring but also the interval-censoring.
It supports two encodings of intervals, `interval` and `interval2`[^survival-interval-encoding]; I use the former, which format works well with both the `survival` library and also other tools like JAGS.
Times are written as minutes since midnight, so they can be handled as positive numbers rather than date-times (ie. midnight=0, 11AM=660, noon=720, midnight=1440, etc), and the upper and lower bounds on intervals are 0 and 1440 (so if I check the mail at 660 and it's there, then the interval is 0-660, and if it's not, 660-1440).
[^survival-interval-encoding]: From the documentation:
> `Surv(time, time2, event, type="interval")`
>
> 1. `time`: For interval data, the first argument is the starting time for the interval.
> 2. `time2`: ending time of the interval for interval censored or counting process data only. Intervals are assumed to be open on the left and closed on the right, `(start, end]`. For counting process data, event indicates whether an event occurred at the end of the interval.
> 3. `event`: The status indicator, normally 0=alive, 1=dead....For interval censored data, the status indicator is 0=right censored, 1=event at time, 2=left censored, 3=interval censored.
>
> Interval censored data can be represented in two ways. For the first use `type = "interval"` and the codes shown above. In that usage the value of the `time2` argument is ignored unless `event=3`. The second approach is to think of each observation as a time interval with _(-∞, t)_ for left censored, _(t, ∞)_ for right censored, _(t,t)_ for exact and _(t~1~, t~2~)_ for an interval. This is the approach used for `type = "interval2"`. Infinite values can be represented either by actual infinity (`Inf`) or `NA`. The second form has proven to be the more useful one.
>
> ...a subject's data for the pair of columns in the dataset `(time1, time2)` is _(t~e~, t~e~)_ if the event time _t~e~_ is known exactly; _(t~l~, NA)_ if right censored (where _t~l~_ is the censoring time); and _(t~l~, t~u~)_ if interval censored (where _t~l~_ is the lower and _t~u~_ is the upper bound of the interval).
~~~{.R}
# Routines to make it easier to work in minutes-since-midnight:
library(lubridate)
fromClock <- function(ts){ (hour(ts)*60) + minute(ts) + (second(ts)/60)}
toClock <- function(t) {
h <- floor(t/60)
m <- floor(t - h*60)
sprintf("%0.2d:%0.2d", h, m) }
set.seed(2015-06-21)
# simulate a scenario in which the mailman tends to come around 11AM (660) and I tend to check around then,
# & generate interval data for each time, bounded by end-of-day/midnight below & above, collecting ~1 month:
simulateMailbox <- function(n, time) {
deliveryTime <- round(rnorm(n, mean = time, sd = 30))
checkTime <- round(rnorm(n, mean = time, sd = 20))
simulates <- mapply(function (ck, dy) { if(ck>dy) { return(c(0,ck)) } else { return(c(ck,1440)) }},
checkTime, deliveryTime)
return(data.frame(Time1=simulates[1,], Time2=simulates[2,])) }
mailSim <- simulateMailbox(30, 650); mailSim
## Time1 Time2
## 1 620 1440
## 2 0 651
## 3 0 627
## 4 624 1440
## 5 629 1440
## 6 664 1440
## 7 665 1440
## 8 652 1440
## ...
library(ggplot2)
png(file="~/wiki/doc/statistics/decision/mail-delivery/gwern-simulated.png", width = 800, height = 500)
ggplot(mailSim) + geom_segment(aes(x=Time1, xend=Time2, y=1:nrow(mailSim), yend=1:nrow(mailSim))) +
geom_vline(xintercept=650, color="blue") + ylab("Day") + xlab("Time")
invisible(dev.off())
~~~
Inferring the mean time of delivery might sound difficult with such extremely crude data of intervals 700 minutes wide or worse, but plotting the little simulated dataset and marking the true mean time of 650, we see it's not *that* bad---the mean time is probably whatever line passes through the most intervals:
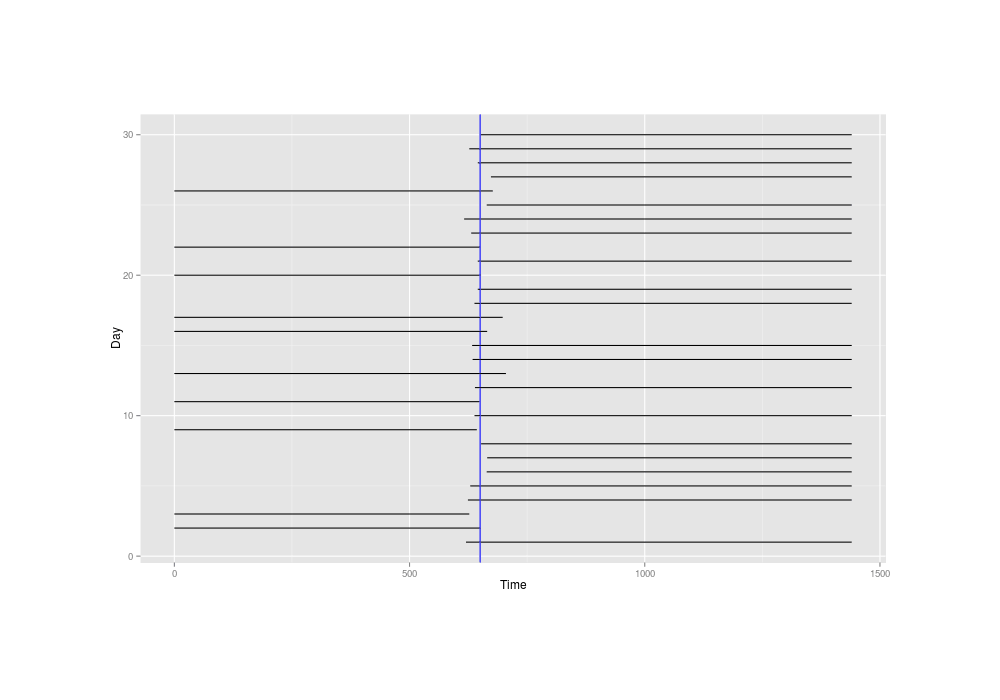
And also with our simulated dataset, we can see if the standard R survival library and an interval-censored model written in JAGS can recover the 650:
~~~{.R}
library(survival)
surv <- Surv(mailSim$Time1, mailSim$Time2, type="interval2")
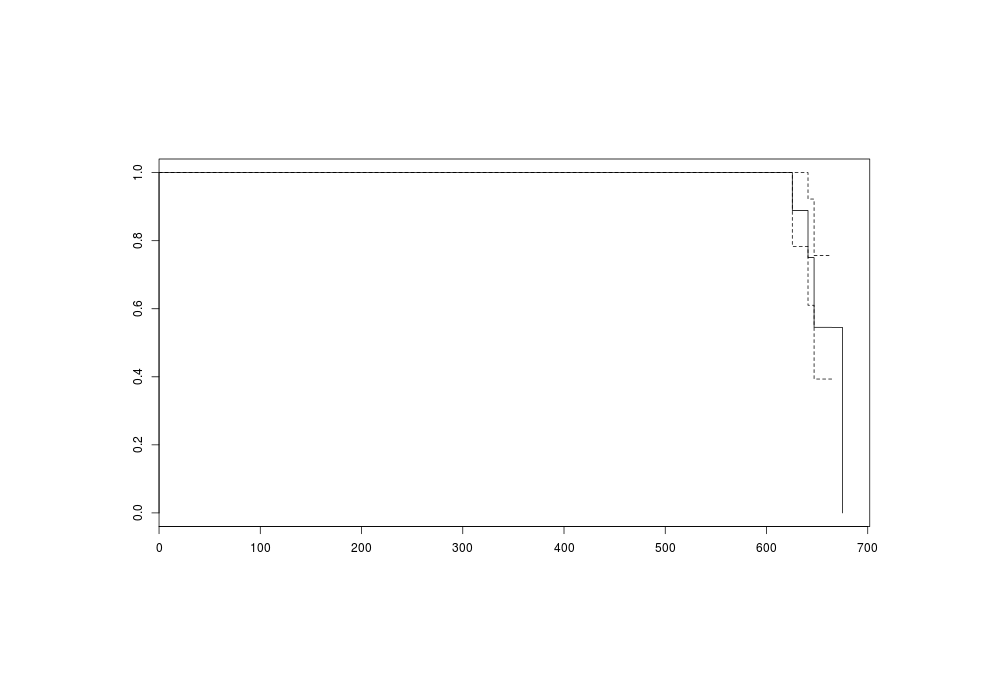
s <- survfit(surv ~ 1, data=mailSim); summary(s)
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 625.5 30.0000 3.33599e+00 0.888800 0.0573976 0.783131 1.000000
## 641.0 26.6640 4.15541e+00 0.750287 0.0790267 0.610339 0.922323
## 647.0 22.5086 6.14506e+00 0.545451 0.0909091 0.393449 0.756178
## 651.5 16.3635 3.84506e-11 0.545451 0.0909091 0.393449 0.756178
## 664.5 16.3635 5.82315e-03 0.545257 0.0909124 0.393258 0.756005
## 675.0 16.3577 1.63577e+01 0.000000 NaN NA NA
plot(s)
png(file="~/wiki/doc/statistics/decision/mail-delivery/gwern-simulated-survivalcurve.png", width = 800, height = 500)
plot(s)
invisible(dev.off())
sr <- survreg(surv ~ 1, dist="gaussian", data=mailSim); summary(sr)
## Value Std. Error z p
## Value Std. Error z p
## (Intercept) 663.08028 9.742171 68.06289 0.00000e+00
## Log(scale) 3.41895 0.438366 7.79931 6.22465e-15
##
## Scale= 30.5374
##
## Gaussian distribution
## Loglik(model)= -15.8 Loglik(intercept only)= -15.8
## Number of Newton-Raphson Iterations: 11
## n= 30
~~~
### MCMC
More Bayesianly, we can write an interval-censoring model in JAGS, which gives us the opportunity to use an informative prior about the mean time the mailman comes.
They work normal 9-5 hours as far as I know, so we can rule out anything outside 540-1020.
From past experience, I expect the mail to show up not before 10AM (600) and not after 1PM (780), with those extremes being rare and sometime around 11AM (650) being much more common; so not an uniform distribution over 600-780 but a normal one centered on 650 and then somewhat arbitrarily saying that 600-700 represent 3 SDs out from the mean of delivery times to get SD=~30 minutes so in all, `dnorm(650, pow(30, -2))`.
The SD itself seems to me like it could range anywhere from a few minutes to an hour, but much beyond that is impossible (if the SD was over an hour, then every so often the mailman would have to come at 8AM! and if it was smaller than 10 minutes, then I would never have noticed much variation in the first place).
~~~{.R}
library(R2jags)
model1 <- function () {
for (i in 1:n){
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dnorm(mu,tau)
}
mu ~ dnorm(650, pow(30, -2))
sd ~ dunif(10, 60)
tau <- pow(1/sd, 2)
y.new ~ dnorm(mu, tau)
}
# y=1 == Event=3 for `Surv`: event is hidden inside interval, not observed/left-/right-censored
data <- list("dt"=mailSim, "n"=nrow(mailSim), "y"=rep(1, nrow(mailSim)))
inits <- function() { list(mu=rnorm(1),sd=30,t=as.vector(apply(mailSim,1,mean))) }
params <- c("mu", "sd", "y.new")
j1 <- jags(data,inits, params, model1); j1
## mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
## mu 665.055 9.841 647.724 658.092 664.334 670.983 686.264 1.008 280
## sd 40.153 11.592 18.626 30.643 40.813 49.707 59.048 1.047 51
## y.new 664.103 42.908 577.518 637.561 663.011 689.912 749.936 1.002 1300
## deviance 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
~~~
Both approaches' point-value mean time of 663-665 (11:03-11:05AM) come close to the true simulation value of 650 (11AM) and the prediction interval of 577-749 also sounds right, validating the models.
The estimated standard deviation isn't as accurate with a wide credible interval, reflecting that it's a harder parameter to estimate and the estimate is still vague with only _n_ = 30.
With a simulation and JAGS set up, we could also see how the posterior estimates of the mean, 95% CI of the mean, and predictive interval change as an additional datapoint is added:
~~~{.R}
animatePosteriors <- function (df, filename, upperTrue, lowerTrue) {
# https://cran.r-project.org/web/packages/animation/index.html
library(animation)
saveGIF(
for(n in 1:nrow(df)){
data <- list("dt"=df[1:n,], "n"=nrow(df[1:n,]), "y"=rep(1, nrow(df[1:n,])))
inits <- function() { list(mu=rnorm(1),sd=30,t=as.vector(apply(df[1:n,],1,mean))) }
params <- c("mu","sd", "y.new")
j1 <- jags(data, inits, params, model1, progress.bar="none")
lowerMean <- j1$BUGSoutput$summary[c(2),][3]
medianMean <- j1$BUGSoutput$mean$mu
upperMean <- j1$BUGSoutput$summary[c(2),][7]
lowerPredictive <- j1$BUGSoutput$summary[c(4),][3]
upperPredictive <- j1$BUGSoutput$summary[c(4),][7]
## WARNING: need an environment call for `ggplot` inside a function for local variables like
## 'n' to be visible: https://stackoverflow.com/a/29595312/329866
## WARNING: & you can't just call qplot due to animation/ggplot2 bug; have to assign & print
timeLimits <- seq(from=9*60, to=12.8*60, by=15)
p <- ggplot(df[1:n,], environment = environment()) +
coord_cartesian(xlim = timeLimits) +
scale_x_continuous(breaks=timeLimits, labels=sapply(timeLimits, toClock)) +
ylab("Day") + xlab("Time") +
geom_segment(aes(x=df[1:n,]$Time1, xend=df[1:n,]$Time2, y=1:n, yend=1:n)) +
geom_vline(xintercept=medianMean, color="blue") +
geom_vline(xintercept=lowerMean, color="green") +
geom_vline(xintercept=upperMean, color="green") +
geom_vline(xintercept=lowerPredictive, color="red") +
geom_vline(xintercept=upperPredictive, color="red") +
geom_vline(xintercept=lowerTrue, color="red4") +
geom_vline(xintercept=upperTrue, color="red4")
print(p)
},
interval = 0.7, ani.width = 800, ani.height=800,
movie.name = filename) }
simData <- simulateMailbox(200, 650)
confintTrue <- round(qnorm(c(0.025, 0.975), mean=650, sd=30))
lowerPredictiveTrue <- confintTrue[1]
upperPredictiveTrue <- confintTrue[2]
animatePosteriors(simData, "/home/gwern/wiki/image/maildelivery/simulated-inferencesamplebysample.gif", lowerPredictiveTrue, upperPredictiveTrue)
~~~
**Simulated data: posterior estimates of mail delivery times, evolving sample by sample for 200 datapoints.**
The estimated mean time is in [blue]{.smallcaps}, 95% CI around the mean time in [green]{.smallcaps}, and [lines]{.smallcaps} are 95% predictive intervals as to when the delivery is made
Probably the most striking aspect of watching these summaries updated datum by datum, to me, is how the estimate of the mean homes in almost immediately on close to the true value (this isn't due solely to the informative prior either, as with a completely uninformative `dunif(0,1440)` will zoom in within 4 or 5 datapoints as well, after some violent thrashing around).
What happens is that the intervals initially look uninformative if the first two or three all turn out to be delivered/non-delivered and so the mean delivery time could still be anywhere from ~11:AM-midnight or vice-versa, but then as soon as even one needle falls the other way, then the mean suddenly snaps into tight focus and gets better from there.
While I understand this abrupt transition in hindsight (only a tiny subset of values around the overlapping tips of the needles can yield the observed flip-flops of delivery/non-delivery, while a mean time far from the tips would yield a completely consistent dataset of all deliveries/non-deliveries), I didn't expect this, simply reasoning that "one interval-censored datum seems very uninformative, so it must take many data to yield any sort of decent result for the mean & standard deviation and hence the predictions".
But, even as the mean becomes precisely estimated, the predictive interval---which is what, in the end, we really care about---remains obdurate and broad, because we assume the delivery time is generated by a normal distribution and so the predicted delivery times are the product of not just the mean but the standard deviation as well, and the standard deviation is hard to estimate (a 95% credible interval of 12-51!).
Also in hindsight this is predictable as well, since the flip-flopping needles may be sensitive to the mean, but not to the spread of delivery-times; the data would not look much different than it does if the mailman could deliver anywhere from 8AM to 3PM---on early days she delivers a few hours before I check the mailbox around 11AM and on late days she delivers a few hours after.
These considerations also raise questions about statistical power/optimal experiment design: what are the best times to sample from interval-censored data in order to estimate as precisely as possible with a limited budget of samples?
I searched for material on interval-censored data but didn't find anything directly addressing my question.
The flip-flops suggest that to estimate the mean, one should sample only at the current estimated mean, which maximizes the probability that there will be a net 50-50 split of delivery/non-delivery; but where should one sample for the SD as well?
~~~{.R}
mailInterval <- data.frame(
Date=as.POSIXct(c( "2015-06-20 11:00AM", "2015-06-21 11:06AM", "2015-06-23 11:03AM",
"2015-06-24 11:05AM", "2015-06-25 11:00AM", "2015-06-26 10:56AM",
"2015-06-27 10:45AM", "2015-06-29 10:31AM", "2015-06-30 10:39AM", "2015-07-01 10:27AM",
"2015-07-02 10:47AM", "2015-07-03 10:27AM", "2015-07-04 10:54AM", "2015-07-05 10:55AM",
"2015-07-06 11:21AM", "2015-07-07 10:01AM", "2015-07-08 10:20AM", "2015-07-09 10:50AM",
"2015-07-10 11:10AM", "2015-07-11 11:12AM", "2015-07-13 11:05AM", "2015-07-14 11:14AM",
"2015-07-15 11:40AM", "2015-07-16 11:24AM", "2015-07-17 11:03AM", "2015-07-18 10:46AM",
"2015-07-20 11:05AM", "2015-07-21 10:56AM", "2015-07-22 11:00AM", "2015-07-23 11:17AM",
"2015-07-24 11:15AM", "2015-07-27 11:11AM", "2015-07-28 10:44AM", "2015-07-29 11:18AM",
"2015-07-30 11:08AM", "2015-07-31 10:44AM", "2015-08-01 11:25AM", "2015-08-03 10:45AM",
"2015-08-04 10:45AM", "2015-08-05 10:44AM", "2015-08-06 10:33AM", "2015-08-07 10:55AM",
"2015-08-10 11:09AM", "2015-08-11 11:16AM", "2015-08-12 11:14AM", "2015-08-13 11:10AM",
"2015-08-14 11:02AM", "2015-08-15 11:04AM", "2015-08-18 11:15AM", "2015-08-20 11:20AM",
"2015-08-22 11:46AM", "2015-08-23 11:04AM", "2015-08-24 10:56AM", "2015-08-25 10:26AM",
"2015-08-26 11:57AM", "2015-08-27 10:15AM", "2015-08-31 12:35PM", "2015-09-01 11:44AM",
"2015-09-02 10:54AM", "2015-09-03 10:29AM", "2015-09-04 10:08AM", "2015-09-05 10:45AM",
"2015-09-07 10:58AM", "2015-09-08 10:25AM", "2015-09-09 10:29AM", "2015-09-10 10:48AM",
"2015-09-16 11:22AM", "2015-09-17 11:06AM", "2015-09-18 11:22AM", "2015-09-19 11:12AM",
"2015-09-21 11:52AM", "2015-09-23 12:02PM", "2015-09-24 10:00AM", "2015-09-25 12:08PM",
"2015-09-26 10:59AM", "2015-09-28 10:57AM", "2015-09-29 10:52AM" ),
"EDT"),
Delivered=c(FALSE, FALSE, TRUE, TRUE, TRUE, TRUE, TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, FALSE,
FALSE, TRUE, FALSE, FALSE, FALSE, TRUE, TRUE, FALSE, TRUE, TRUE, TRUE, TRUE, FALSE,
FALSE, FALSE, TRUE, TRUE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE,
FALSE, FALSE, FALSE, FALSE, TRUE, TRUE, TRUE, TRUE, TRUE, FALSE, TRUE, TRUE, FALSE,
FALSE, FALSE, TRUE, FALSE, TRUE, TRUE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE,
FALSE, FALSE, TRUE, TRUE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE))
mailInterval$Time <- fromClock(mailInterval$Date)
mail <- with(mailInterval, data.frame(Time1 = ifelse(Delivered, 0, Time),
Time2 = ifelse(Delivered, Time, 1440)))
library(R2jags)
model1 <- function() { for (i in 1:n){
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dnorm(mu,tau)
}
mu ~ dnorm(650, pow(30, -2))
sd ~ dunif(10, 60)
tau <- pow(1/sd, 2)
y.new ~ dnorm(mu, tau)
}
data <- list("dt"=mail, "n"=nrow(mail), "y"=rep(1, nrow(mail)))
inits <- function() { list(mu=rnorm(1),sd=30,t=as.vector(apply(mail,1,mean))) }
params <- c("mu","sd", "y.new")
j1 <- jags(data, inits, params, model1, n.iter=100000); j1
## mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
## mu 658.173 4.468 649.098 655.469 658.156 660.943 666.797 1.001 3000
## sd 27.138 7.976 16.034 21.417 25.459 30.916 48.149 1.001 3000
## y.new 658.098 27.960 601.899 640.912 657.942 675.067 712.985 1.001 3000
## deviance 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
animatePosteriors(mail, "/home/gwern/wiki/image/maildelivery/real-inferencesamplebysample.gif", 0, 0)
~~~
Real data: posterior estimates of mail delivery times, animated updated sample by sample
### ABC
Because JAGS provides an interval-censored distribution in the form of `dinterval()` with a [likelihood function](!W), we can use MCMC for inverse inference (reasoning from data to the underlying process)
But if it didn't, I wouldn't know how to write one down for it and then the MCMC wouldn't work; but I was able to write a little simulation of how the underlying process of delivery-and-checking works, which, given a set of parameters, spits out simulated results generated by the process, which is probability or forward inference (reasoning from a version of an underlying process to see what it creates).
This is a common situation: you can write a good simulation simply by describing how you think something works, but you can't write a likelihood function.
[ABC](!W "Approximate Bayesian computation") (exemplified in the fun example ["Tiny Data, Approximate Bayesian Computation and the Socks of Karl Broman"](https://www.sumsar.net/blog/2014/10/tiny-data-and-the-socks-of-karl-broman/); see also Wilkinson's [intro](https://darrenjw.wordpress.com/2013/03/31/introduction-to-approximate-bayesian-computation-abc/ "Introduction to Approximate Bayesian Computation (ABC)") & [summary statistics](https://darrenjw.wordpress.com/2013/09/01/summary-stats-for-abc/ "Summary stats for ABC") posts) is a remarkably simple and powerful idea which lets us take a forward simulation and use it to run backwards inference.
(Reminds me a little of [Solomonoff induction](!W "Solomonoff’s theory of inductive inference").)
There's [an R package, of course](https://cran.r-project.org/web/packages/abc/index.html) which implements nice features & optimizations, but ABC is so simple we might as well write our own for transparency.
The simplest ABC goes like this:
You sample possible parameters from your prior, feed the set of parameters into your simulation, and if the result is identical to your data, you save that set of parameters.
At the end, you're left with a bunch of sets and that's your posterior distribution which you can look at the histograms of and calculate 95% densities etc.
So for the mail data, ABC goes like this:
~~~{.R}
simulateMailbox <- function(n, dTime, dSD) {
deliveryTime <- round(rnorm(n, mean = dTime, sd = dSD))
checkTime <- round(rnorm(n, mean = dTime, sd = dSD))
simulates <- mapply(function (ck, dy) { if(ck>dy) { return(c(0,ck)) } else { return(c(ck,1440)) }},
checkTime, deliveryTime)
return(data.frame(Time1=simulates[1,], Time2=simulates[2,])) }
# if both data-frames are sorted, comparison is easier
mailSorted <- mail[order(mail$Time1),]
mail_sim <- replicate(100000, {
# mu ~ dnorm(650, 20)
mu <- rnorm(n=1, mean=650, sd=20)
# sd ~ dunif(10, 60)
sd <- runif(n=1, min=10, max=60)
newData <- simulateMailbox(nrow(mailSorted), mu, sd)
newDataSorted <- newData[order(newData$Time1),]
if (all(newDataSorted == mailSorted)) { return(c(Mu=mu, SD=sd)) }
}
)
results <- Filter(function(x) {!is.null(x)}, mail_sim)
results <- data.frame(t(sapply(results,c)))
summary(results)
~~~
The first thing to note is efficiency: I can get a reasonable number of samples in reasonable amount of time for _n_ = 1-3, but at 4 datapoints, it becomes slow.
There's so many possible datasets when 4 checks are simulated that almost all get rejected because they are not identical to the real dataset and it takes millions of samples and hours to run.
And this problem only gets worse for _n_ = 5 and bigger.
To run ABC more efficiently, you relax the requirement that the simulated data == real data and instead accept the pair of parameters if the simulated data is 'close enough' in some sense to the real data, close in terms of some summary statistic (hopefully sufficient) like the mean.
I don't know what are the sufficient statistics for a set of interval-censored data, but I figure that if the means of the pairs of times are similar in both datasets, then they are probably close enough for ABC to work, so I can use that as a rejection tolerance; implementing that and playing around, it seems I can make the difference in means as tight as <1 while still running fast.
~~~{.R}
mail_abc <- function(samples) {
results <- list()
n <- 0
while (n 2014
wilcox.test(TimeDelivered ~ Group, data=mailExact)
wilcox.test(TimeDelivered ~ Group, conf.int=TRUE, data=mailExact)
# Wilcoxon rank sum test with continuity correction
#
# data: TimeDelivered by Group
# W = 105.5, p-value = 0.004344224
# alternative hypothesis: true location shift is not equal to 0
# 95% confidence interval:
# 18.99997358 67.00004597
# sample estimates:
# difference in location
# 41.00004647
sd(mailExact[mailExact$Group,]$TimeDelivered)
## [1] 20.03603473
~~~
Why might there be two clusters?
Well, now that I think about it, I recall that my mailman used to be an older gentleman with white hair (I remember him vividly because in mid-August 2013 a package of fish oil was damaged in transit, and he showed up to explain it to me and offer suggestions on returns; Amazon didn't insist on a leaky fish oil bottle being shipped back and simply sent me a new one).
But now my mailman is a younger middle-aged woman. That seems like a good reason for a shift in delivery times---perhaps she drives faster.
(As our mailpersons never interact with customers and there is minimal road traffic, the delivery times should reflect almost entirely their route length, delivery volume, and driving speed/efficiency.)
Alternately, perhaps the personnel shift was driven by a changed route; the exact cause is unimportant as the difference appears large and consistent.
### MCMC
Estimating the two distributions separately in a simple multilevel/hierarchical model:
~~~{.R}
model2 <- function() {
# I expect all deliveries ~11AM/650:
grand.mean ~ dnorm(650, pow(20, -2))
# different mailman/groups will deliver at different offsets, but not by more than 2 hours or so:
delta.between.group ~ dunif(0, 100)
# similarly, both mailman times and delivery times are reasonably precise within 2 hours or so:
tau.between.group <- pow(sigma.between.group, -2)
sigma.between.group ~ dunif(0, 100)
for(j in 1:K){
# let's say the group-level differences are also normally-distributed:
group.delta[j] ~ dnorm(delta.between.group, tau.between.group)
# and each group also has its own standard-deviation, potentially different from the others':
group.within.sigma[j] ~ dunif(0, 100)
group.within.tau[j] <- pow(group.within.sigma[j], -2)
# save the net combo for convenience & interpretability:
group.mean[j] <- grand.mean + group.delta[j]
}
for (i in 1:N) {
# each individual observation is from the grand-mean + group-offset, then normally distributed:
Y[i] ~ dnorm(grand.mean + group.delta[Group[i]], group.within.tau[Group[i]])
}
# prediction interval for the second group, the 2015 data, which is the one I care about:
y.new2 ~ dnorm(group.mean[2], group.within.tau[2])
}
data <- list(N=nrow(mailExact), Y=mailExact$TimeDelivered, K=max(mailExact$Group+1),
Group=(mailExact$Group+1))
params <- c("grand.mean","delta.between.group", "sigma.between.group", "group.delta", "group.mean",
"group.within.sigma", "y.new2")
k1 <- jags(data=data, parameters.to.save=params, inits=NULL, model.file=model2, n.iter=50000); k1
## mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
## delta.between.group 39.252 24.676 1.866 19.228 35.892 56.239 90.804 1.002 1900
## grand.mean 646.541 18.229 610.306 634.420 646.967 658.402 682.334 1.001 3000
## group.delta[1] 51.451 24.090 6.461 35.024 51.243 67.678 97.720 1.001 3000
## group.delta[2] 14.603 18.634 -22.068 2.057 14.234 26.874 51.781 1.001 3000
## group.mean[1] 697.992 16.997 660.532 688.781 699.057 707.816 731.813 1.001 3000
## group.mean[2] 661.144 4.493 652.375 658.188 661.171 664.057 670.275 1.002 1500
## group.within.sigma[1] 36.006 16.775 15.685 23.966 31.571 42.990 81.056 1.001 3000
## group.within.sigma[2] 21.297 3.461 15.764 18.798 20.929 23.266 28.987 1.002 1400
## sigma.between.group 44.831 24.254 7.910 25.429 41.149 62.391 94.998 1.004 1500
## y.new2 661.669 22.141 616.927 647.494 661.905 675.973 704.147 1.002 3000
## deviance 252.499 3.557 247.820 249.767 251.785 254.502 261.130 1.001 3000
##
## For each parameter, n.eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
##
## DIC info (using the rule, pD = var(deviance)/2)
## pD = 6.3 and DIC = 258.8
~~~
## Combined data
Combining the interval and exact data is easy: exact data are interval data with very narrow intervals (accurate roughly to within half a minute), where the beginning and end match.
If exact delivery time is available for a day, then the interval data for that day is omitted as redundant:
~~~{.R}
mail2 <- rbind(
with(mailExact,
data.frame(Date=Date,
Time1 = TimeDelivered,
Time2= TimeDelivered + 0.5)),
with(mailInterval[!(as.Date(mailInterval$Date) %in% as.Date(mailExact$Date)),],
data.frame(Date=Date,
Time1 = ifelse(Delivered, 0, Time),
Time2 = ifelse(Delivered, Time, 1440))))
mail2$Group <- year(mail2$Date) > 2014
mailCombined <- subset(mail2,select=c("Time1","Time2"))
~~~
The multilevel model is the same as before with the exception that the likelihood needs to be tweaked to put `dinterval` on top, and the input data needs to be munged appropriately to match its expectations of it being a two-column data-frame of the form `(Time1,Time2)`:
~~~{.R}
model3 <- function() {
grand.mean ~ dnorm(650, pow(20, -2))
delta.between.group ~ dunif(0, 100)
tau.between.group <- pow(sigma.between.group, -2)
sigma.between.group ~ dunif(0, 100)
y.new2015 ~ dnorm(group.mean[2], group.within.tau[2])
for(j in 1:K){
group.delta[j] ~ dnorm(delta.between.group, tau.between.group)
group.within.sigma[j] ~ dunif(0, 100)
group.within.tau[j] <- pow(group.within.sigma[j], -2)
group.mean[j] <- grand.mean + group.delta[j]
}
for (i in 1:N) {
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dnorm(grand.mean + group.delta[Group[i]], group.within.tau[Group[i]])
}
}
data2 <- list(N=nrow(mail2), K=max(mail2$Group+1),
Group=(mail2$Group+1), "dt"=subset(mail2, select=c("Time1", "Time2")),
"y"=rep(1, nrow(mail2)))
params2 <- c("grand.mean","delta.between.group", "sigma.between.group", "group.delta", "group.mean",
"group.within.sigma", "y.new2015")
inits2 <- function() { list(grand.mean=650, t=as.vector(apply(data2[["dt"]],1,mean))) }
k2 <- jags(data=data2, parameters.to.save=params2, inits=inits2, model.file=model3, n.iter=100000); k2
## mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
## delta.between.group 39.364 24.229 2.728 19.947 36.568 56.187 92.219 1.002 3000
## grand.mean 646.921 18.303 609.659 634.911 647.471 659.948 680.647 1.002 1200
## group.delta[1] 51.517 23.431 7.242 35.480 50.876 67.432 97.720 1.002 1300
## group.delta[2] 15.617 18.463 -18.505 2.450 15.254 27.661 53.121 1.002 1100
## group.mean[1] 698.438 16.892 661.420 689.057 699.582 708.741 730.282 1.001 3000
## group.mean[2] 662.538 3.088 656.700 660.463 662.538 664.545 668.783 1.001 3000
## group.within.sigma[1] 36.074 16.210 16.181 24.249 31.834 43.555 80.031 1.001 2500
## group.within.sigma[2] 20.691 2.933 15.832 18.616 20.342 22.421 27.245 1.001 3000
## sigma.between.group 43.801 24.304 6.174 24.458 39.747 60.546 95.167 1.003 3000
## y.new2015 662.168 21.331 620.004 648.164 661.859 675.705 705.655 1.002 1200
## deviance 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
~~~
It's worth comparing the `y.new2015` (the posterior predictive distribution for just 2015, ignoring the earlier cluster) and the original `y.new` (computed on 2015 interval-censored data): we started with a 95% credible interval of mail deliveries in the window 601-712 (10:01AM-11:52AM), and then got a window of 620-702 (10:20AM-11:45), for a gain of half an hour or almost 30%.
And this despite having almost 3x as much interval-censored data!
The lesson here is to try to minimize the length of intervals if one wants to make precise inferences.
## Model checking
### On Model Uncertainty
> ...It is no surprise that when this model fails, it is the [likelihood](!W "Likelihood function") rather than the [prior](!W "Prior probability") that is causing the problem. In the binomial model under consideration here, the prior comes into the posterior distribution only once and the likelihood comes in _n_ times. It is perhaps merely an accident of history that **skeptics and subjectivists alike strain on the gnat of the prior distribution while swallowing the camel that is the likelihood.**
>
> [Andrew Gelman](!W), 2013^[Emphasis added; ["'Not Only Defended But Also Applied': The Perceived Absurdity of Bayesian Inference"](http://www.stat.columbia.edu/~gelman/research/published/feller8.pdf), Gelman & Robert 2013; ["The prior can generally only be understood in the context of the likelihood"](https://arxiv.org/abs/1708.07487), Gelman et al 2017.]
In setting up an analysis, one must [make a variety of choices](http://www.stat.columbia.edu/~gelman/research/unpublished/p_hacking.pdf "'The garden of forking paths: Why multiple comparisons can be a problem, even when there is no `fishing expedition` or `p-hacking` and the research hypothesis was posited ahead of time', Gelman & Loken 2013") in what models to use, which influences the result; this neglect of "model uncertainty" can lead to overconfident inferences or miss critical details.
In Bayesian analyses, typically the prior comes in for the most scrutiny as to how it determines the result; but the prior part of the model often has much less influence than the structural or functional form of the analysis, where it is assumed that the outcome is drawn from a normal distribution or another such common choice, although it's not.
This choice itself is often arbitrary and can determine the result almost regardless of what the data says.
For example, the normal distribution has thin tails and so the probability of something being far out on a tail will be extremely small and combined with other considerations like measurement error, can result in a model refusing to ever accept that a value really is 'extreme' without equally extreme amounts of data---a refusal that would not happen if any of a number of other perfectly possible distributions had been chosen instead like log-normal distribution or [Cauchy distribution](!W)---despite the fact that the choice of normal distribution itself is usually due more to convenience than any extremely strong evidence that the normal distribution is the true distribution ("every model is false, but some are useful"), which means the best response is simply to note that [one man's modus ponens is another man's modus tollens](/modus "'One Man’s Modus Ponens', Branwen 2012")---the probability that [one's math or model is wrong is far higher](/math-error "'The Existential Risk of Math Errors', Branwen 2012") sets an upper bound on how much we can get out of them, and a bound which often bars many of the inferences one might try to extract from them.
For example:
#. the normal distribution is commonly used for its analytic tractability and asymptotic properties, but it has some aspects that are, in a sense, *too* powerful and restrictive: specifically, that its tails are thin. Thin tails can cause serious underestimations of rare phenomenon (and not just in cases involving power laws) and can lead to absurdly powerful conclusions. Two examples:
- in [one analysis of charities](https://www.lesswrong.com/posts/RdpqsQ6xbHzyckW9m/why-we-can-t-take-expected-value-estimates-literally-even "Why We Can't Take Expected Value Estimates Literally (Even When They're Unbiased)"), the writer uses normal distributions and thus winds up arguing that with error in our assessments of charities' values, our estimate must be shrunken far towards the mean (which is entirely true); but [this is circular](https://www.lesswrong.com/posts/JyH7ezruQbC2iWcSg/bayesian-adjustment-does-not-defeat-existential-risk-charity), since by assuming normal distributions he has also assumed away the existence of large differences in value between charities.
If one were to grant the apparently innocuous assumption of normally distributed effectiveness of interventions, one would be forced to ignore that there *are* large differences---consider [knitting sweaters for penguins](https://web.archive.org/web/20111025143342/http://www.giantflightlessbirds.com/2011/10/the-great-penguin-sweater-fiasco/ "The Great Penguin Sweater Fiasco") vs [stopping children from being infected by parasites](!W "Schistosomiasis Control Initiative") or [killed by malaria](!W "Against Malaria Foundation"); are they really within a few standard deviations of each other? Should we really ignore interventions like vaccines which claim to save lives at a cost of no more than tens of thousands of dollars, on the grounds that most charities require hundreds of thousands or millions of dollars to achieve goals like that? If we look at [Global Burden of Disease](!W) and see extreme skews in what causes loss of QALYs, with some classifications being hundreds or thousands of times more damaging than others (like indoor fires), is it more likely that the data is wrong than right solely because the normal distribution says that the largest problems are many standard deviations out? It's clear that whatever the right distribution for modeling charity or health outcomes is, it is probably not literally & exactly a normal distribution and it should allow for large differences; and having abandoned the normal, we then lose the apparently magical ability to make confident predictions about how many charities are how effective.
- [in another analysis](https://polymatharchives.blogspot.com/2015/01/the-inappropriately-excluded.html), the author, a Michael Ferguson, argues that American society discriminates to a truly astonishing degree against people with high IQs, claiming that people with 150IQ have 97% less chance of achieving success than people with the ideal IQ of ~133, and thus, that past that, the chance of success drops almost to 0%, and that this is due to vicious constant discrimination & persecution. His analysis takes the strategy of noting the population IQ is normally distributed, by definition, at 𝑁(100,15) and taking a few old studies of elite groups like students at Harvard Medical School and noting the studies report means like 122 and standard deviations like 6, inferring the students are normally distributed at 𝑁(122,6), and then noting that when these two normal distributions are superimposed, there will be almost no elites as high as IQ 140 or 150 despite there being many such people in the general population and this underrepresentation gets more and more extreme as one goes further out on the tail; why did all the high IQ population members fail to show up in the elite distribution? It must be discrimination. Thus, he grimly warns his readers that "If your IQ is over 150, it is a clarion call; without direct intervention, your career prospects are very poor. If you are the parent of a child with a D15IQ over 150, immediate and dramatic action is required."
This would be a remarkable fact if true for many reasons (not least the waste & damage to science and humanity), but that is unlikely: because the underrepresentation is a mathematical necessity of the normal distribution due to the elite distribution being defined as having a smaller SD. The assumption that the elite distribution is normal drives the entire remarkable, unlikely result. But why assume elites are normally distributed? Most of the processes by which elite schools such as Harvard would select from the general population would *not* produce a normal distribution: if selected at a SAT threshold, the result will not be normal but a truncated normal; if selected on multiple factors such as test scores and personality, it will more likely be log-normal; and so on. That the studies of the Harvard students reported a mean and SD does not show that the student distribution was normal, and in fact, it's easy to simulate scenarios like the threshold model or a model in which increasing IQ produces increasing odds of admission, and show that the reported means & SDs are entirely possible under other highly non-normal distributions (intuitively, people as high as 140 or 150 are so rare that they don't affect the summary statistics much, regardless of whether they are heavily discriminated against or heavily favored for admission). The shocking conclusion follows from the mathematical/statistical assumption, but where did this assumption come from and should we grant it?
#. linear models have a similar problem as normal distributions: while convenient and simple, they have well-known problems when at the extremes of the data or when projected beyond that. Textbooks give examples like a linear regression on ice cream sales predicting negative sales during the winter, or predicting that sales in summer will be orders of magnitude higher, and it's easy to make up other examples like a linear regression on sprinting times predicting that in another century, sprinters will finish races before they have started. Linear models have no problems predicting negative values backwards in time, or predicting absurdly high amounts in the far future, but they are convenient and for the most part, it's easy to simply ignore the nonsensical predictions or, if they're causing problems, use a technical fix like logging values, switching to a log-normal distribution (with its strictly natural support), using a sigmoid or logarithmic fit to account for the inevitable flattening out, handle ratio data with beta regression, fix the end-values with spline regression, etc; if we make the mistake of modeling a bacterial population in an agar dish as an exponentially increasing population, we'll soon learn otherwise than the sigmoid or logistic curves make a better fit. Mark Twain offered an amusing criticism in _[Life on the Mississippi](!W)_, and indeed, one can often detect model problems watching for instances where one gets "wholesale returns of conjecture out of such a trifling investment of fact", for that indicates that we may be engaged in postulating, which has all "the advantages of theft over honest toil":
> In the space of one hundred and seventy-six years the Lower Mississippi has shortened itself two hundred and forty-two miles. That is an average of a trifle over one mile and a third per year. Therefore, any calm person, who is not blind or idiotic, can see that in the Old Oolitic Silurian Period, just a million years ago next November, the Lower Mississippi River was upwards of one million three hundred thousand miles long, and stuck out over the Gulf of Mexico like a fishing-rod. And by the same token any person can see that seven hundred and forty-two years from now the Lower Mississippi will be only a mile and three-quarters long, and Cairo and New Orleans will have joined their streets together, and be plodding comfortably along under a single mayor and a mutual board of aldermen. There is something fascinating about science. One gets such wholesale returns of conjecture out of such a trifling investment of fact.
An interesting use of OLS linear models is given in [Sharov & Gordon 2013](https://arxiv.org/abs/1304.3381 "Life Before Earth"), which follows up a [2006 paper](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1526419/ "'Genome increase as a clock for the origin and evolution of life', Sharov 2006"). By taking the [genome length](!W "Genome size") of 8 biological groups (eg. prokaryote genomes are ~5 logged and prokaryotes originated 3-4bya, so it is assumed that genome lengths were 5 3-4bya) and regressing against date of origin (on a log scale), their linear model, in the mother of all extrapolations, extrapolates backwards to the smallest possible genome (and hence, origin of all life) around 9 billion years ago---well before Earth could have supported life or even existed, and consistent only with a panspermia hypothesis.
This is problematic for a number of reasons: genome length is being used as a clock, but the animal and bacteria genomes involved are all *contemporary* (since no DNA older than a million years or so has ever been recovered or the full length counted) which raises some questions about why we think genome length has any connection with time and how exactly this linear increase process is supposed to work (is evolution supposed to have stopped for the prokaryotes 3-4bya and their genome lengths been static ever since?); how they defined those particular taxonomic groups of all the possibilities and those particular genome lengths & dates (and a questionable reason for excluding plants); measurement error and the very small data set implies considerable uncertainty in the estimates & a rejection of Earthly origins even at face value; genome lengths seem to have little to do with the passage of time but reflect peculiarities of biology & selection (viruses are under more selection pressure, and have faster generations than, any other kind of organism, and have innovated baffling numbers of tricks for infection, and yet instead of having ultra-long genomes reflecting these endless generations and innovation, they have ultra-small ones; and similarly, the Human Genome Project yielded humbling results in showing the human genome to be smaller than many organisms we humans look down upon, such as even some single-cell organisms, which can be bizarrely huge like the ferns, [Mimivirus](!W)) and vary tremendously within groups; there is no direct evidence showing that early life's genome lengths increased at the claimed trendline, and no particular reason to expect recent trends to hold exactly to the origins of life and times when life may not have been DNA-based or even RNA-based at all; genomes are known to shrink in size as well as increase under the right conditions (and one would hope that contemporary prokaryotes are more genetically efficient than the earliest prokaryotes); mutation load & transcription errors place an upper bound on how large a genome *can* be ([Ohno 1972](/doc/genetics/selection/1972-ohno.pdf "An Argument for the Genetic Simplicity of Man and other Mammals")); many genomic phenomenon like retroviral insertions or selfish jumping [transposons](!W "Transposable element"); it's unclear why one should endorse constant increase in genome size rather than a population genetics perspective of equilibriums and occasional shifts; horizontal gene flow makes it unclear how much one can compare with multicellular organisms & vertical transmission; Gould argues that any increase in complexity can be due to a random walk with a lower bound, in which case there is no underlying trend at all, merely stochastic extremes occasionally reached; and the wide variations in "[junk DNA](!W)" cannot be explained if genome length has much at all to do with a clock ticking since divergence from other species.
More relevantly here is the model misspecification: the model will happily project past 1bpa and estimate how long the genomes were---in negative units---in 10bya. (To say nothing of extrapolating a few billion years into the future.) This is nonsensical: whatever life may use for genomes, it must be positive and never negative. So linearity is known a priori to be false and to break down at some point: the linear model is guaranteed to be incorrect in its predictions early in history; now, if one must reject the extrapolations for 10bya because the model has broken down by that point, why should one believe the projections from before the breakdown...? Why not infer that any linearity appears only later, after such regime-changing events as the creation of life, the switch to DNA, the expansion over the entire world, the oxygen catastrophe, etc? (If your ice cream linear model predicts selling -1000 ice cream cones at the North Pole, why believe it when it predicts selling -10 ice cream cones in Canada?) Why not use a model like a sigmoid which at least has a chance of being correct? The problem, of course, is that if one tried to fit a sigmoid or another such distribution or curve which could fit the true data, one would discover that there is no early data which could give any indication of how fast genome lengths were increasing very early on like in 4bya, since all the available data is from *now*. Where does the idea come from that genome lengths would increase slowly even in the first life forms which discovered a virgin planet of unexploited organic goop? Examined closely, since there is no evidence for early linearity, we see that the modeling produces no additional evidence, and is merely an exercise of showing the consequences of an assumption: "if one assumes that genome lengths increase linearly [...] then with this particular set of lengths and assumed times, it logically follows that the first organisms was 9bya". This is a thoroughly bizarre premise which cannot survive the slightest contact with known sizes of genomes and influences, so one gets no more out of this than what one put in: since there was no particular reason to accept that assumption out of all possible assumptions, there's no additional reason to accept the conclusion as true either. On its own, it cannot give us any additional evidence for panspermia.
#. independence is often a questionable model assumption: many datapoints are highly correlated with each other and calculations assuming independence will become grotesquely overconfident. Is it more likely that the probability of a tied election is 10^-90^ and one could run trillions of elections without ever once coming near a tie, or that [the binomial assumption is simply wrong about voters](https://statmodeling.stat.columbia.edu/2014/12/25/common-sense-statistics/) being independent and victory margins being accordingly distributed? Is it more likely that stock market movements are thin-tailed and large crashes would happen only once in billions of years, or that crashes are common and the distribution is fat-tailed? Is it more likely that there are many strong predictors of human populations' wealth and social factors, or that they are [highly correlated with neighbors due to descent & proximity & common geographic conditions](!W "Galton’s problem")? Is it more likely that the models were correct and the fisheries just accidentally collapsed, or that the models did not take into account autocorrelation/multilevelness and overstated accuracy through [pseudoreplication](!W)? etc
In the case of mail deliveries, there's clearly model uncertainty.
While I used the [normal distribution](!W), I could as easily have used [_t_-distributions](!W "Student’s t-distribution") (fatter-tailed normals), [log-normals](!W "Log-normal distribution"), [exponentials](!W "Exponential distribution"), [uniforms](!W "Uniform distribution (discrete)"), [betas](!W "Beta distribution"), [overdispersed](!W "Overdispersion") versions of some of the previous, or picked some even more exotic [univariate distribution](https://www.math.wm.edu/~leemis/chart/UDR/UDR.html "Univariate Distribution Relationships") and easily come up with a just-so story for some of them.
(It's a negative-binomial because we're modeling minutes until "failure" ie delivery; no, [it's a log-normal](/note/pipeline "'Leaky Pipelines', Branwen 2014") because each phase in the mail processing pipeline and each stop slows down the mailman and delays multiply; no, it's a normal distribution because each stop merely *adds* a certain amount of time, and the sum of many small random deviates is itself normally distributed; no, it's a _t_-distribution because sometimes the mail arrives much earlier or later and it's a more robust distribution we should be using anyway; no, it's even wider than that and an uniform distribution because the mailman starts and ends their shift at particular times but otherwise doesn't care about speed; no, it's a beta distribution over time because that's more flexible and can include the others as special-cases...)
Model uncertainty can be handled several ways ([Hooten & Hobbs 2015](https://www.stat.colostate.edu/~hooten/papers/pdf/Hooten_Hobbs_EcolMono_2015.pdf "A guide to Bayesian model selection for ecologists")), including:
- Penalty or regularization or sparsity priors (only handles selection of variables/predictors; gains largely eliminated in this case by informative priors)
- Diagnostics like posterior predictive checks, crossvalidation, and [AIC](!W "Akaike information criterion")/[BIC](!W "Bayesian information criterion")/[DIC](!W "Deviance information criterion")/[WAIC](https://arxiv.org/abs/1208.6338 "'A Widely Applicable Bayesian Information Criterion', Watanabe 2012") ([overview](http://www.stat.columbia.edu/~gelman/research/published/waic_understand3.pdf "'Understanding predictive information criteria for Bayesian models', Gelman et al 2013")) can be used to check for lack of fit; but like tests in software development, they can only show the presence of bugs & not their absence
- Maximally flexible models can be used like nonparametric Bayesian models; if "all models are wrong", we can use models which are arbitrarily flexible in order to minimize the influence of our model misspecification ([Dunson 2013](/doc/statistics/bayes/2013-dunson.pdf "Nonparametric Bayes"))
- [Ensemble approaches](!W "Ensemble learning") (often targeted at the narrow use-case of selecting variables/predictors in a linear model, but some are applicable to choosing between different distributions as well), particularly Bayesian approaches ([popularization](https://www.lesswrong.com/posts/iyRpsScBa6y4rduEt/model-combination-and-adjustment); [Friel & Wyse 2011](https://arxiv.org/abs/1111.1957 "Estimating the model evidence: a review"); [Hooten & Hobbs 2015](https://www.stat.colostate.edu/~hooten/papers/pdf/Hooten_Hobbs_EcolMono_2015.pdf "A guide to Bayesian model selection for ecologists")):
- Bayesian model choice: models can be pitted against each other (eg. using Bayes factors) implemented using [nested sampling](!W), or [reversible jump MCMC](!W)/product-space method ([Carlin & Chib 1995](https://www.ma.imperial.ac.uk/~das01/MyWeb/SCBI/Papers/CarlinChib.pdf "Bayesian model choice via Markov chain Monte Carlo methods"), [Lodewyckx et al 2011](https://ejwagenmakers.com/2011/LodewyckxEtAl2011.pdf "A tutorial on Bayes factor estimation with the product space method") & [source code](https://ppw.kuleuven.be/okp/software/scripts_tut_bfepsm/), [Tenan 2014](/doc/statistics/bayes/2014-tenan.pdf "Bayesian model selection: The steepest mountain to climb") & [source code](/doc/statistics/bayes/2014-tenan-supplement.zip)), or ABC, and the one with highest posterior probability is selected for any further analysis while all others are ignored
- Bayesian model averaging: posterior probabilities of models are calculated, but all models are retained and their posteriors are combined weighted by the probability that model is the true one ([Hoeting et al 1999](https://projecteuclid.org/download/pdf_1/euclid.ss/1009212519 "Bayesian model averaging: a tutorial")); but with enough data, the posterior probability of the model closest to the truth will converge on 1 and BMA becomes a model selection procedure
- Bayesian model combination: posterior probabilities of combinations/ensembles of models are calculated, yielding a richer set of 'models' which often outperform all of the original models; such as by learning an optimal weighting in a linear combination ([Monteith et al 2011](https://axon.cs.byu.edu/papers/Kristine.ijcnn2011.pdf "Turning Bayesian Model Averaging Into Bayesian Model Combination"))
Of the non-ensemble approaches: regularization is already done via the informative priors; some of the diagnostics might work but others won't (JAGS won't calculate DIC for interval-censored data); nonparametric approaches would be too challenging for me to implement in JAGS and I'm not sure there is enough data to allow the nonparametric models to work well.
This leaves PPC, crossvalidation, and the ensemble approaches:
- Bayesian model combination is overkill
- Bayesian model averaging, given Bayesian model choice, may also be overkill and not meaningfully improve predictions enough to change final decisions about mail check times
- Bayesian model choice: nested sampling doesn't seem applicable, leaving reversible-jump/product-space; while JAGS examples are available in tutorial papers, I found them lengthy & complicated by using realistic data & models, hardwired to their specific use-case still too difficult to understand with my limited JAGS skills. So I wound up implementing using ABC.
### PPC
Posterior predictive checks (PPC) are a technique recommended by Gelman as a test of how appropriate the model is (as the model or likelihood often is far more important in forcing particular results than the priors one might've used), where one generates possible observations from the model and inferred posteriors, and sees how often the simulated data matches the real data; if that is rarely or never, then the model may be bad and one should fix it or possibly throw in additional models for Bayesian model comparison (which will hopefully then pick out the right model).
For continuous data or more than trivially small data, we have the same issue as in ABC (which is similar to PPCs): the simulates will never exactly match the data, so we must define some sort of summary or distance measure which lets us say that a particular simulated dataset is similar enough to the real data.
In the two summaries I tried for ABC, counting 'flip-flops' worked better, so I'll reuse that here.
For the simulation, we also need check or interval-censoring times, which I also treat as a normal distribution & estimate their means and SDs from the original data.
~~~{.R}
posteriorTimes <- k2$BUGSoutput$sims.list[["y.new2015"]]
simsPPC <- replicate(10000, {
nChecks <- nrow(mail)
checkTimes <- c(mail[mail$Time1>0,]$Time1, mail[mail$Time2<1440,]$Time2)
meanCheck <- mean(checkTimes)
sdCheck <- sd(checkTimes)
deliveryTime <- sample(posteriorTimes, size=nChecks, replace=TRUE)
checkTime <- round(rnorm(nChecks, mean = meanCheck, sd = sdCheck))
newSamples <- mapply(function (ck, dy) { if(ck>dy) { return(c(0,ck)) } else { return(c(ck,1440)) }},
checkTime, deliveryTime)
newData <- data.frame(Time1=newSamples[1,], Time2=newSamples[2,])
return(sum(newData$Time1 == 0))
}
)
png(file="~/wiki/doc/statistics/decision/mail-delivery/gwern-ppc.png", width = 800, height = 500)
qplot(simsPPC) + geom_vline(xintercept=sum(mail$Time1 == 0), color="blue")
invisible(dev.off())
~~~
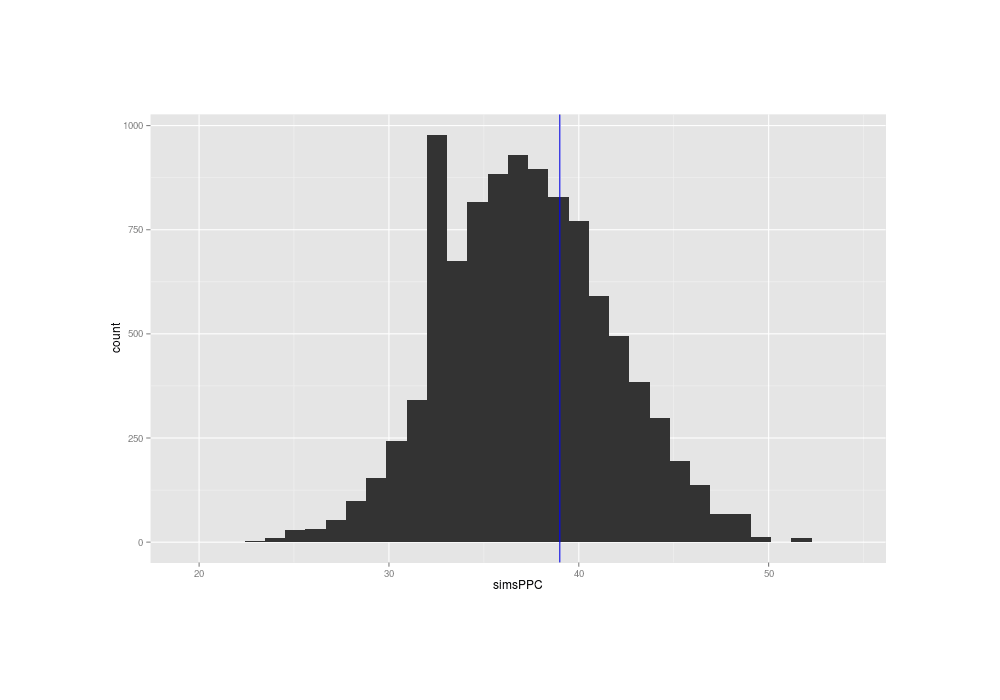
The true data has a summary near the middle of the distribution of the summaries of the posterior predictions, suggesting that the normal distribution's fit to the problem is OK (at least, when considered in isolation).
### Crossvalidation
CV comes in several flavors, but since the data is not big, I can use leave-one-out crossvalidation.
The usual error measures are unavailable due to interval-censoring, so after some pondering, I went with a zero-one loss based on whether a delivery is predicted or not at a particular check-time.
Mean-squared-error is out due to the intervaling, as are variants like absolute error. Thinking about it some, it seems to me that each datapoint is really made of two things: the check-time, and delivery status. The check-time has nothing to do with the model quality and the model isn't trying to predict it; what I want the model to predict is whether the mail is delivered or not *if* I were to check at particular times. The check-time is the predictor variable and the delivery-status is the response variable.
So I could ask the model's posterior predictive distribution of delivery-times (`y.new`) whether or not the mail would or would not be delivered at a particular time, and compare it against the held-out datapoint's actual delivery status, 1 if the model correctly predicts delivered/not-delivered and 0 if it predicts the opposite of what the data said. (So a zero-one loss.)
The base-rate of delivery vs non-delivery will be 50-50, so a good model should achieve a better mean zero-one loss than 0.5.
For distributions, we'll compare the normal used all along, the _t_-distribution (for its fatter tails), and a little more exotically, the log-normal & exponential distributions as well.
Of these, the first two are the most likely, and I think it's highly unlikely that the log-normal or exponential could fit better (because they will tend to predict extremely late deliveries, much later than I believe is at all realistic, while the _t_'s spread is more reasonable in accommodating some non-normality but not too much). I include those two just to see what will happen and test out the robustness of any approach used.
The 4 models in JAGS:
~~~{.R}
modelN <- "model { for (i in 1:n){
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dnorm(mu,tau)
}
mu ~ dnorm(650, pow(30, -2))
sd ~ dunif(10, 60)
tau <- pow(1/sd, 2)
y.new ~ dnorm(mu, tau) }"
modelT <- "model { for (i in 1:n){
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dt(mu,tau,nu)
}
nu ~ dexp(1/30)
mu ~ dnorm(650, pow(30, -2))
sd ~ dunif(10, 60)
tau <- pow(1/sd, 2)
y.new ~ dnorm(mu, tau) }"
modelL <- "model { for (i in 1:n) {
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dlnorm(muL, tauL)
}
sd ~ dunif(10, 60)
tauL <- pow(1/log(sd), 2)
mu ~ dnorm(650, pow(30, -2))
muL <- log(mu)
y.new ~ dlnorm(muL, tauL) }"
modelE <- "model { for (i in 1:n){
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dexp(theta)
}
# set the mean ~600, but remember rate is reciprocal:
theta ~ dexp(1/600)
y.new ~ dexp(theta) }"
~~~
Here's a try at implementing leave-one-out crossvalidation for those four JAGS models on the interval-censored mail data with a zero-one loss defined that way based on delivery status:
~~~{.R}
runModel <- function(newData, model, iter=5000) {
# set up and run the model and extract predicted delivery times
data <- list("dt"=newData, "n"=nrow(newData), "y"=rep(1, nrow(newData)))
inits <- function() { list(mu=rnorm(1,mean=600,sd=30),sd=30,t=as.vector(apply(newData,1,mean))) }
params <- c("y.new")
cv1 <- jags(data, inits, params, textConnection(model), n.iter=iter, progress.bar="none")
posteriorTimes <- cv1$BUGSoutput$sims.list[["y.new"]]
return(posteriorTimes)
}
loocvs <- function(dt, model) {
results <- NULL
for (i in 1:nrow(dt)) {
# set up relevant data for this particular fold in the crossvalidation
ith <- dt[i,]
newData <- dt[-i,] # drop the _i_th datapoint
checkTime <- if (ith$Time1==0) { ith$Time2 } else { ith$Time1 }
there <- if (ith$Time1==0) { TRUE } else { FALSE }
posteriorTimes <- runModel(dt, model, iter=500)
# score predictions against heldout data point
results[i] <- mean(sapply(posteriorTimes,
function(t) { if (tcheckTime && !there) { 1 } else { 0 } }}))
}
return(results)
}
loocvsN <- loocvs(mailCombined, modelN)
loocvsT <- loocvs(mailCombined, modelT)
loocvsL <- loocvs(mailCombined, modelL)
loocvsE <- loocvs(mailCombined, modelE)
mean(loocvsN)
## [1] 0.6316747967
mean(loocvsT)
## [1] 0.6339715447
mean(loocvsL)
## [1] 0.4994674797
mean(loocvsE)
## [1] 0.4504227642
~~~
By this measure, the normal & _t_ models perform almost identically, while we can reject log-normal & exponentials out of hand as performing as badly as (or worse than) chance.
### Bayesian Model Selection
We are comparing 4 parametric models here: the normal, Student's _t_, log-normal, and exponential models. (Time permitting, a Cauchy would have been good too.)
The BIC/DIC/WAIC deviance criteria are unavailable; nested sampling cannot handle multiple distributions; this leaves reversible jump MCMC/product-space method and ABC.
I looked at product-space first. The idea is conceptually simple: we take our JAGS models and treat it as a mixture model with each model having a probability of having generated an observation, and since we believe only one is true, after inferring these probabilities, they become our posterior probabilities of each model.
The JAGS implementations look relatively straightforward, but most of them deal with the case of different probabilities or parameters for the same distribution or with variable selection in linear regression, and the only examples with multiple distributions were totally baffling to me, as I became lost in the different distributions and categories and indices and what the 'pseudopriors' are doing etc.
After giving up, it occurred to me that since I had no problem writing the 4 standalone models themselves, their posterior predictive distributions were, in a sense, generative models of themselves and so I could use them in ABC.
If I generated samples from all 4 models in ABC and counted how often they (approximately) matched the original data, then would not the ratios of accepted samples then constitute posterior probabilities or at least Bayes factors? If the normal model matched the data 10x more often than the _t_ model, then surely the normal model is a much better model of the data than the _t_.
But there's nothing new under the sun, and so while the papers on Bayesian model comparison I had read up until that point had not mentioned ABC as an option, it turns out that using ABC for Bayesian model comparison is not just possible but downright common in genetics & ecology (see for background [Fu & Li 1997](http://mbe.oxfordjournals.org/content/14/2/195.full.pdf "Estimating the age of the common ancestor of a sample of DNA sequences"), [Beaumont et al 2002](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1462356/pdf/12524368.pdf "Approximate Bayesian computation in population genetics"), [Marjoram et al 2003](https://www.pnas.org/doi/full/10.1073/pnas.0306899100 "Markov chain Monte Carlo without likelihoods"), [Didelot et al 2004](https://people.maths.bris.ac.uk/~madjl/DidelotEtAlPRE-ABC.pdf "Likelihood-free estimation of model evidence"), [Beaumont 2010](https://math.la.asu.edu/~jtaylor/teaching/Fall2013/APM541/papers/Beaumont2010.pdf "Approximate Bayesian Computation in Evolution and Ecology") & [Sunnaker et al 2013](https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1002803 "Approximate Bayesian Computation"); examples include [Pritchard et al 1999](http://mbe.oxfordjournals.org/content/16/12/1791.full.pdf "Population growth of human Y chromosomes: a study of Y chromosome microsatellites"), [Estoup et al 2004](https://onlinelibrary.wiley.com/doi/abs/10.1111/j.0014-3820.2004.tb00487.x "Genetic analysis of complex demographic scenarios: spatially expanding populations of the cane toad, _Bufo marinus_"), [Miller et al 2005](https://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1255&context=entomologyfacpub "Multiple transatlantic introductions of the Western corn rootworm"), [Pascual et al 2007](/doc/statistics/bayes/2007-pascual.pdf "Introduction history of _Drosophila subobscura_ in the New World: A microsatellite-based survey using ABC methods"), [Francois et al 2008](https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1000075 "Demographic history of European populations of Arabidopsis thaliana"), [Sainudiin et al 2011](/doc/statistics/bayes/2011-sainudiin.pdf "Experiments with the site frequency spectrum")).
There is the issue that the summary statistics may [lose information and lead to bad model comparison results](https://www.pnas.org/doi/full/10.1073/pnas.1102900108 "'Lack of confidence in approximate Bayesian computation model choice', Robert et al 2011"), but there's always tradeoffs.
ABC for Bayesian model comparison:
~~~{.R}
simulateMailboxMulti <- function(n, m, sd, simulation) {
deliveryTime <- sample(simulation, size=n, replace=TRUE)
checkTime <- round(rnorm(n, mean=m, sd=sd))
simulates <- mapply(function (ck, dy) { if(ck>dy) { return(c(0,ck)) } else { return(c(ck,1440)) }},
checkTime, deliveryTime)
return(data.frame(Time1=simulates[1,], Time2=simulates[2,]))
}
mail_abc_bmc <- function(samples) {
# generate the posterior samples for each model, which serve as our generative simulations:
normal <- runModel(mailCombined, modelN)
tdistribution <- runModel(mailCombined, modelT)
lognormal <- runModel(mailCombined, modelL)
exponential <- runModel(mailCombined, modelE)
simulates <- nrow(mailCombined)
# create a distribution for our check times
checkTimes <- c(mailCombined[mailCombined$Time1>0,]$Time1, mailCombined[mailCombined$Time2<1440,]$Time2)
meanCheck <- mean(checkTimes)
sdCheck <- sd(checkTimes)
results <- list()
n <- 0
while (nProbability and Statistics for Business Decisions: An Introduction to Managerial Economics Under Uncertainty', Schlaifer 1959"), [_Applied Statistical Decision Theory_, Raiffa & Schlaifer 1961](/doc/statistics/decision/1961-raiffa-appliedstatisticaldecisiontheory.pdf "'Applied Statistical Decision Theory', Raiffa & Schlaifer 1961"), and the more recent [_Introduction to Statistical Decision Theory_, Pratt et al 1995](/doc/statistics/decision/1995-pratt-introductionstatisticaldecisiontheory.epub); an applied example of going from Bayesian multilevel models to optimal decisions is ["Bayesian prediction of mean indoor radon concentrations for Minnesota counties"](https://stat.columbia.edu/~gelman/research/published/price.pdf "Price et al 1996").)
Since the motivation for estimating mail-delivery time is implicitly a decision-theoretic problem ("at what time *should* I decide to check the mail?"), there's no reason to settle for just a mean or credible interval for the delivery time.
## Optimal mail checking time
With a posterior distribution of delivery times (`y.new`) we can try to find an optimal time to check, assuming we can figure out a [loss function](!W) giving a cost of checking at each possible time.
The loss here can be considered in units of time; if I didn't care about the delay between the package being delivered and me getting my hands on it, I would simply check at 2PM and have done with it.
The usual stopping point in an analysis like this would involve the mean, least-squares, and [mean squared error](!W).
There's a [lot of good things to say about that](https://www.benkuhn.net/squared/ "Why squared error?") as a default
But as an algorithm for deciding when check the mail, squaring errors and averaging them seems like a strange way to evaluate mistakes: is it really *equally* bad to check the mail box 5 minutes before the mail and 5 minutes afterwards? is checking 10 minutes after really *more* than twice as bad as checking 5 minutes after?
I would say "no" in both cases: it's much better to check 5 minutes after rather than 5 minutes before, since then the package will be there and I won't have to make another hike out to the mailbox; and checking 10 minutes seems only twice as bad to me as checking 5 minutes after.
So the loss function itself is not any of the usual suspects: squared loss, absolute loss and 0-1 loss don't correspond to my process of checking mail.
I need to define my own loss function, expressing the real costs and gains of this situation.
### Defining a loss function
Expecting a package wears on my mind and in some cases, I'd like to start using the contents ASAP; I see a delay of 10 minutes as being twice as bad as 5 minutes and not 4 times as bad, so this part is an absolute loss. (If it arrives at 11AM and I check at 11:30AM, then the loss due to the delay is 30.)
Besides the delay, there's also the cost of walking all the way down to the mailbox and back, which due to the long driveway is around 10 minutes, but it's mostly unshaded and hot out and an interruption, so the loss is much greater than that; introspecting, I would be willing to wait at least 60 minutes to save one roundtrip, so I will define the cost of a mail check at 60 'minutes'.
So suppose I check at 10:30AM, the mail comes at 11AM, and I check again at 11:30AM and find it; then the cost is 60 + 60 + (11:30AM − 11:00AM) = 150, while if I had checked at 11:20AM then the cost is better and smaller at just 60 + (11:20AM − 11:00AM) = 70.
OK, so if the package is there, that's easy, but what if I walk out at 11:20AM and it's *not* there?
In a proper [Bayesian search theory](!W) application, if I check once, I would then update my posterior and run a loss function again to decide when to check next, but this is impracticable for daily usage and in reality, what I would do is if the first check didn't turn up the package, I would then give up in frustration & disgust and not come back until ~1PM (780) when the package would definitely have arrived. Then I'd incur a loss of two walks and possibly a long wait until 1PM.
All these considerations give me a weird-looking (but realistic) loss function: if the package is delivered at _d_ and we check at a particular time _t_, then if _t_>_d_ and the package had arrived we incur a total loss of 60 + (_t − d_); otherwise, we check back a second and final time at 1PM, incurring a total loss of 60 + 60 + (780 − _d_).
### Finding the optimum
Having figured that out, we run the loss function on each sample from the posterior, averaging over all weighted possible delivery times, and find what time of day minimizes the loss:
~~~{.R}
lossFunction <- function(t, walk_cost, predictions, lastResortT) {
mean(sapply(predictions,
function(delivered) { if (deliveredbattery adapter, and other wires, would cost >[$80]($2015) for the parts. A [PiJuice Solar](https://www.kickstarter.com/projects/pijuice/pijuice-a-portable-project-platform-for-every-rasp) [would cost](https://uk.pi-supply.com/products/pijuice-solar?v=7516fd43adaa) ~[$80]($2015) but doesn't ship until March 2016 (if ever). So a RP would work if I wanted to go as far as setting up a solar-powered RP, spending easily [$100]($2015)+.
- Arduinos use much less power---around 20 milliamps---and can be reduced to <1 milliamps, in which case, combined with a compatible battery like the [$15]($2015) [Lithium Ion Polymer Battery - 3.7v 2500mAh](https://www.adafruit.com/product/328), power is no longer an issue and the logger could run a week ((2500mAh / 20ma⁄h) / 24 = 7) or months at <1 milliamps. But Arduinos are much more challenging to use than Raspberry Pis---I have no experience in embedded electronics or wiring up such devices or programming in C, and so no confidence I could build it correctly.
The [$22]($2015) [Adafruit Data logger (Adalogger)](https://www.adafruit.com/product/2796) ([documentation](https://learn.adafruit.com/adafruit-feather-32u4-adalogger)), based on the Arduino Uno, combines most of the hardware necessary. That still leaves connecting the reed magnetic switch (eg. ["Seco-Larm SM-226L Garage Door Contacts for Closed Circuits"](https://web.archive.org/web/20140905041605/http://www.smarthome.com/seco-larm-sm-226l-garage-door-contacts-for-closed-circuits.html) ([$11]($2015)), or [magnetic switch](https://www.adafruit.com/product/375) ([$3.95]($2015))), programming the Adalogger, and optimizing power consumption to make recharges not a hassle. This makes it much closer to feasible and I thought seriously about it, but ultimately, I don't think I care enough at the moment about logging mail data to struggle through the learning curve of embedded & electrical engineering knowledge for this particular project.
#. Wilder ideas include running lasers & mirrors; or running a coaxial cable out to the mailbox, putting a photodiode at one end, and keeping the logger inside near a power outlet to resolve the wireless & power issues. (But coax cable does cost money, leaving it exposed is not a good idea considering the riding lawn mower, and digging up hundreds of meters of ground to bury the coax cable does not sound like fun.)
### EVSI
The next kind is what is the "[expected value of sample information](!W)" (EVSI): what is the value of collecting one more additional datapoint, which can help pin down the optimal time a little more precisely and reduce the risk of loss from picking a bad time?
EVSI can be defined as "expected value of best decision with some additional sample information" minus "expected value of best current decision".
More specifically, if many times we created a new datapoint, create an updated posterior distribution incorporating that new datapoint, run the loss function again & calculate a new optimal check time, and compute the improvement of the new check time's NPV over improved estimate of the old check time's NPV to estimate a possible EVSI, what is the mean of the EVSIs?
This tells us the benefit of that datapoint, and then we can subtract the cost of collecting one more datapoint; if it's still positive, we want to collect more data, but if it's negative (the gain from the estimate improved by one more datapoint) is less than a datapoint would cost to collect, then we have hit diminishing returns and it may be time to stop collecting data.
We could do this for one datapoint to decide whether to stop. But we could also go back and look at how the EVSI & profit shrank during the original collection of the mail data.
~~~{.R}
data <- mailCombined
sampleValues <- data.frame(N=NULL, newOptimum=NULL, newOptimumLoss=NULL,
sampleValue=NULL, sampleValueProfit=NULL)
for (n in seq(from=0, to=(nrow(data)+10))) {
evsis <- replicate(10, {
# if n is more than we collected, bootstrap hypothetical new data; otherwise,
# just take that prefix and pretend we are doing a sequential trial where we
# have only collected the first n observations thus far
if (n > nrow(data)) { newData <- rbind(data,
data[sample(1:nrow(data), n - nrow(data) , replace=TRUE),]) } else {
newData <- data[1:n,] }
kEVSIN <- runModel(newData, modelN)
kEVSIT <- runModel(newData, modelT)
posteriorTimesEVSI <- c(kEVSIN, kEVSIT) # model averaging
lossesEVSI <- sapply(c(0:1440), function (tm) { lossFunction(tm, 60, posteriorTimesEVSI, 780);})
# compare to the estimate based on priors if no data yet:
if (n==0) { oldOptimum <- min(lossesEVSI) } else {
oldOptimum <- lossesEVSI[sampleValues[sampleValues$N==0,]$newOptimum] }
newOptimum <- min(lossesEVSI)
sampleValue <- netPresentValue(newOptimum - oldOptimum)
sampleValueProfit <- sampleValue + (n*60)
return(list(N=n, newOptimum=which.min(lossesEVSI), newOptimumLoss=newOptimum,
sampleValue=sampleValue, sampleValueProfit=sampleValueProfit))
}
)
sampleValues <- rbind(sampleValues,
data.frame(N=n,
newOptimum=mean(unlist(evsis[2,])),
newOptimumLoss=mean(unlist(evsis[3,])),
sampleValue=mean(unlist(evsis[4,])),
sampleValueProfit=mean(unlist(evsis[5,]))))
}
sampleValues
## N newOptimum newOptimumLoss sampleValue sampleValueProfit
## 1 0 712.600 126.6888958 0.00000000 0.0000000000
## 2 1 712.575 126.7579219 -11.93854006 48.0614599416
## 3 2 719.980 122.3724436 -121.31501738 -1.3150173784
## 4 3 708.150 126.9706051 -32.03379518 147.9662048193
## 5 4 701.790 127.9095775 -143.35714066 96.6428593445
## 6 5 696.695 128.8701531 -299.02233338 0.9776666227
## 7 6 692.440 129.8191319 -466.05452337 -106.0545233747
## 8 7 688.695 132.0807898 -633.09206632 -213.0920663197
## 9 8 690.765 129.5727029 -542.78513810 -62.7851380951
## 10 9 687.660 132.0364916 -681.32564291 -141.3256429125
## 11 10 689.210 130.2163274 -597.48233962 2.5176603795
## 12 11 686.395 130.5338326 -758.15486682 -98.1548668161
## 13 12 687.455 128.6273025 -695.28046012 24.7195398753
## 14 13 691.525 129.2092477 -496.05481084 283.9451891562
## 15 14 695.410 129.2232888 -347.92312703 492.0768729651
## 16 15 693.405 128.1591433 -433.22087565 466.7791243520
## 17 16 693.650 127.0530983 -436.23463412 523.7653658752
## 18 17 693.735 125.5236645 -444.81276457 575.1872354295
## 19 18 695.725 125.3049938 -355.24354368 724.7564563236
## 20 19 693.155 123.7840402 -465.57031668 674.4296833227
## 21 20 691.340 122.2890257 -573.81903972 626.1809602784
## 22 21 695.460 124.4854690 -373.66455168 886.3354483178
## 23 22 693.835 123.3286284 -453.72808090 866.2719190994
## 24 23 692.890 122.1550798 -511.31873755 868.6812624468
## 25 24 691.585 120.6627142 -594.94760901 845.0523909901
## 26 25 689.930 119.8993341 -688.68789781 811.3121021938
## 27 26 690.845 118.8742591 -644.53601191 915.4639880893
## 28 27 693.915 120.5363205 -480.27587034 1139.7241296593
## 29 28 695.455 120.5722357 -410.57354380 1269.4264562033
## 30 29 693.720 119.8216438 -491.01196669 1248.9880333079
## 31 30 692.560 118.5479051 -566.54877290 1233.4512271013
## 32 31 691.265 117.4006005 -642.81873824 1217.1812617638
## 33 32 694.800 120.2531077 -443.02993834 1476.9700616613
## 34 33 694.500 122.6974736 -444.15880135 1535.8411986539
## 35 34 693.200 121.6848098 -506.60101893 1533.3989810750
## 36 35 695.640 123.1766613 -377.44505442 1722.5549455769
## 37 36 695.055 125.0534433 -389.10082564 1770.8991743593
## 38 37 694.210 124.1294044 -439.58662308 1780.4133769227
## 39 38 694.610 123.0556714 -424.08194842 1855.9180515813
## 40 39 694.310 124.7484991 -436.35444597 1903.6455540347
## 41 40 694.505 123.4282826 -429.85235414 1970.1476458589
## 42 41 694.280 122.2800503 -437.52664626 2022.4733537369
## 43 42 695.660 121.9807264 -395.84245846 2124.1575415363
## 44 43 697.795 123.4574969 -298.08161577 2281.9183842337
## 45 44 696.745 122.5201770 -345.76139793 2294.2386020661
## 46 45 695.845 121.6540080 -389.60085022 2310.3991497771
## 47 46 695.090 120.9569570 -436.42100092 2323.5789990833
## 48 47 693.990 120.5449101 -483.41266155 2336.5873384516
## 49 48 694.305 120.7051254 -487.09162861 2392.9083713904
## 50 49 693.840 120.1719436 -499.45106193 2440.5489380720
## 51 50 693.940 119.9749612 -504.81034896 2495.1896510352
## 52 51 693.960 119.9420246 -500.28329793 2559.7167020736
## 53 52 693.595 119.7075089 -512.73745021 2607.2625497905
## 54 53 693.875 119.4981456 -515.01771496 2664.9822850449
## 55 54 693.505 119.1947709 -524.05689719 2715.9431028079
## 56 55 693.900 119.5021316 -517.24622527 2782.7537747290
## 57 56 693.715 119.1529502 -536.63625754 2823.3637424644
## 58 57 693.530 118.7091686 -531.78528869 2888.2147113139
## 59 58 703.2 110.3450586 -237.308410317 3242.691589683
## 60 59 702.8 110.1431462 -260.940058947 3279.059941053
## 61 60 701.8 109.8245030 -292.138648235 3307.861351765
## 62 61 702.0 109.6607867 -313.445660084 3346.554339916
## 63 62 701.7 109.9572132 -324.525787515 3395.474212485
## 64 63 701.0 109.5939801 -353.833817911 3426.166182089
## 65 64 700.9 109.7948883 -353.210103148 3486.789896852
## 66 65 701.3 109.5571512 -343.780758960 3556.219241040
## 67 66 701.2 109.5838684 -310.806893360 3649.193106640
## 68 67 701.5 109.4677088 -316.910308982 3703.089691018
## 69 68 700.9 109.3539013 -326.340338587 3753.659661413
## 70 69 702.1 109.2574961 -317.820011152 3822.179988848
## 71 70 701.2 108.8563787 -351.667974044 3848.332025956
## 72 71 701.2 108.9809869 -339.661339561 3920.338660439
## 73 72 701.5 108.9430690 -313.603261282 4006.396738718
## 74 73 701.6 108.6864327 -324.919641986 4055.080358014
## 75 74 701.4 108.7176209 -308.707536711 4131.292463289
## 76 75 703.1 108.4620179 -304.882851775 4195.117148225
## 77 76 701.7 108.4129922 -303.134783733 4256.865216267
## 78 77 702.2 108.2194238 -304.295347052 4315.704652948
## 79 78 701.4 107.7256569 -334.733360207 4345.266639793
## 80 79 700.4 108.1555870 -340.454520356 4399.545479644
## 81 80 701.8 108.1089954 -315.865705672 4484.134294328
## 82 81 701.7 107.8976325 -332.239957494 4527.760042506
## 83 82 701.3 108.1263477 -318.440927654 4601.559072346
## 84 83 701.7 107.9807588 -341.667394085 4638.332605915
## 85 84 701.6 107.9223031 -332.374354544 4707.625645456
## 86 85 702.3 107.7032516 -329.594428046 4770.405571954
## 87 86 701.2 107.7025934 -323.337539932 4836.662460068
## 88 87 702.6 107.7341694 -315.319855307 4904.680144693
## 89 88 702.7 107.5978394 -318.888777193 4961.111222807
## 90 89 701.7 107.6826961 -329.601897440 5010.398102560
## 91 90 701.2 107.2913853 -352.893246270 5047.106753730
## 92 91 702.6 107.9162503 -298.859548680 5161.140451320
## 93 92 701.4 107.3265408 -345.735043576 5174.264956424
## 94 93 702.9 107.7535692 -307.027575009 5272.972424991
## 95 94 700.7 106.9934449 -380.611482059 5259.388517941
## 96 95 702.2 108.2833572 -318.195906366 5381.804093634
qplot(sampleValues$N, round(sampleValues$newOptimum))
~~~
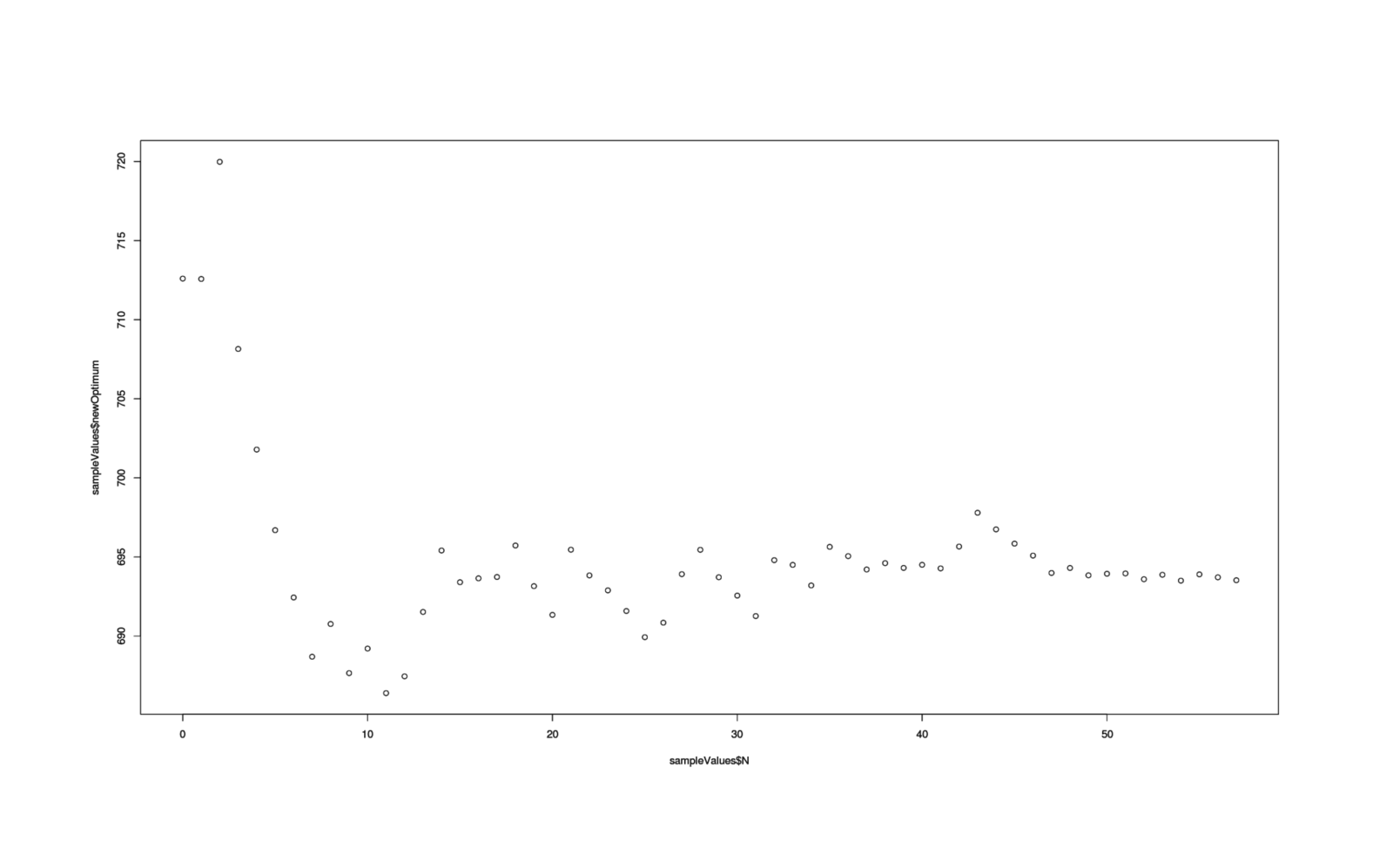{.width-full}
This would suggest that diminishing returns were reached early on (possibly the informative priors had done more work than I appreciated).
The graph shows the estimated optimal mail-check time (700=11:40AM etc) as each datapoint was collected.
You can see that with the priors I set, they were biased towards too-late mail times but as more data comes in, the new optimal check-time drifts steadily downwards until the bias of the prior has been neutralized and now it begins to follow a random walk around 695, with the final estimated mailchecktime being ~693/11:33AM
And at around n=48, diminishing returns has set in so hard that the decision actually stops changing entirely, it's all small fluctuations around 693.
When you include the cost of gathering data, the analysis says you should collect up to _n_ = 13 and then stop (after that, the loss does not decrease but begins to increase because each datapoint inflates costs by +60, and we want to minimize loss); at _n_ = 13, one decides to check at 687/11:27AM, which is close to the 693 which was estimated with 4x more data (!).
So this is interesting: by using informative priors and then taking a decision-theoretic approach, in this case I can make high-quality decisions on surprisingly little data; I could have halted data gathering much earlier.
(Additional data does have benefits in letting me verify the diminishing returns by seeing how the optimal decision hardly changes, can be used for more accurate model averaging, and could be used to model time-varying trends like the large increases in late deliveries during the holidays. But ultimately I have to agree with the EVSI: I didn't need to collect all the data I did.)
# Conclusions
Lessons learned:
#. ABC is as simple to implement and incredibly general as promised; with ABC, it's defining good summary statistics & getting computational tractability which you need to worry about (besides making it tedious to use, long runtimes also interfere with writing a correct implementation in the first place)
#. while powerful, JAGS models can be confusing to write; it's easy to lose track of what the structure of your model is and write the wrong thing, and the use of precision rather than standard-deviation adds boilerplate and makes it even easier to get lost in a welter of variables & distributions, in addition to a fair amount of boilerplate in running the JAGS code at all---leading to errors where you are not certain whether you have a conceptual problem or your boilerplate has drifted out of date
#. the combination of `ggplot2` and [`animation`](https://cran.r-project.org/web/packages/animation/index.html) bade fair to make animations as easy as devising a ggplot2 image, but due to some ugly interactions between them (`ggplot2` interacts with the R top-level scope/environment in a way which breaks when it's called inside a function, and `animation` has some subtle bug relating to deciding how long to delay frames in an animation which I couldn't figure out), I lost hours to getting it to work at all.
#. my original prior estimate of when the mailman comes was accurate, but I seem to have substantially underestimated the standard deviation and there turned out to be considerably model uncertainty about thin tails (normal) vs fatter tails (_t_); despite that, providing informative priors meant that the predictions from the JAGS model were sensible from the start (mostly from the small values for the SD, as the mean time was easily estimated from the intervals) and it made good use of the data.
#. the variability of mail delivery times is high enough that the prediction intervals are inherently wide; after relatively few datapoints, whether interval or exact, diminishing returns has set in.
#. Subjective Bayesianism & decision theory go together like peanut butter & chocolate.
It's all just samples and posterior distributions; want to calculate expected information gains to optimize your sampling, or compare to subjective loss to decide in a principled fashion when to stop? No problem. (Instead of ad hoc rules of thumbs like going for 80% power or controlling alpha at 0.05 or trial sequential analysis stopping at an arbitrary effect size confidence interval...) Long computations are a small price to pay for approximate answers to the right questions rather than exact answers to the wrong questions.
The major downside is that Bayesian decision theory is honored mostly in the breach: I found much more discussion than application of it online, and few worked-out examples in R that I could try to compare with my own implementations of the ideas.
# Appendix
## Thompson sampling
Given a Bayesian model and a reinforcement-learning setting like checking the mailbox, it seems natural to use [Thompson sampling](!W) to guide checks and do [online](!W "Online machine learning") [reinforcement learning](!W) ("online" here meaning learning 1 data point at a time).
I didn't want to reorganize my mornings around such an algorithm, but in reading up on Thompson sampling, I found no source code for any uses outside the stereotypical 3-4 arm binomial bandit, and certainly nothing I could use.
Thompson sampling turns out to be as simple as advertised.
Each time a Ts agent acts, it updates its model based on current data and then simply draws one possible set of parameters at random from its posterior distributions of those parameters; then it finds the optimal action under that particular set of parameters; and executes it.
An implementation of Thompson sampling for this problem, and a test harness to run it on a simulated version of mail-checking to see how it performs in terms of actions, losses, and regret:
~~~{.R}
library(R2jags)
model1 <- function() { for (i in 1:n){
y[i] ~ dinterval(t[i], dt[i,])
t[i] ~ dnorm(mu,tau)
}
mu ~ dnorm(650, pow(30, -2))
sd ~ dunif(10, 60)
tau <- pow(1/sd, 2)
y.new ~ dnorm(mu, tau)
}
lossPosterior <- function(t, walk_cost, predictions, lastResortT) {
sapply(predictions,
function(delivered) { if (delivered