LessWrong and cryonics
How does LessWrong usage correlate with cryonics attitudes and signup rates?
Back in December 2012, Yvain noticed something odd in the 201214ya Lesswrong survey’s cryonic responses: splitting between LW ‘veterans’ and ‘newbies’, the newbies estimated a low probability that cryonics would work and none were signed up (as one would expect) but among the veterans, despite a sixth of them being signed up (an astonishingly high rate compared to the general population), their estimated probability was not higher than the newbies but lower (the opposite of what one would expect). This is surprising since you would expect the estimated probability and the signup rates in various subgroups to move in the same direction: if one group believes cryonics is sure to work, then they will be more likely to decide the expense and social stigma are worth it; while if another group is certain cryonics cannot work, none of them will be signed up. So this result was a bit odd. This pattern also seemed to replicate in the 201313ya survey results as well:
Proto-rationalists thought that, on average, there was a 21% chance of an average cryonically frozen person being revived in the future. Experienced rationalists thought that, on average, there was a 15% chance of same. The difference was marginally significant (p < 0.1).
…On the other hand, 0% of proto-rationalists had signed up for cryonics compared to 13% of experienced rationalists. 48% of proto-rationalists rejected the idea of signing up for cryonics entirely, compared to only 25% of experienced rationalists. So although rationalists are less likely to believe cryonics will work, they are much more likely to sign up for it. Last year’s survey shows the same pattern.
Yvain’s explanation for this anomaly is that it reflects the veterans’ greater willingness to ‘play the odds’ and engage in activities with positive expected value even if the odds are against those activities paying off, and that this may be a causal effect of spending time on LW. (Although of course there’s other possibilities: eg. older LWers may be drawn more from hardcore transhumanists with good STEM or statistical experience, explaining both aspects of the pattern; newer LWers, especially ones brought in by Yudkowsky’s Harry Potter and the Methods of Rationality novel, may be more likely to be from the general population or humanities.)
The figures Yvain use are the population averages (a 2x2 contingency table of experienced vs signed-up), however, and not the result of individual-level regressions. That is, as pointed out by Mitchell Porter, these figures may be driven by issues like Simpson’s paradox. For example, perhaps among the veterans, there’s two populations - some optimists with very high probabilities who all sign up, but also many pessimists with very low probabilities (low enough to slightly more than counterbalance the optimists) who never sign up; in this hypothetical, there is no one who is both pessimistic and signed up (as predicted by the averages), yet, the numbers come out the same way. Just from the overall aggregate numbers, we can’t see whether something like this is happening, and after a quick look at the 201313ya data, Mitchell notes:
…“experienced rationalists” who don’t sign up for cryonics have an average confidence in cryonics of 12%, and “experienced rationalists” who do sign up for cryonics, an average confidence of 26%.
Is this right?
Statistical Considerations
A few things make this question a bit challenging to investigate. We don’t have as much data as we think we have, and analysis choices can reduce that a great deal:
being signed up for cryonics is rare (ALCOR has a grand total of 1,062 people signed up worldwide, and 144 cryopreserved members), and while there are relatively a lot of cryonicsers on LW, they’re still rare. Rare things are hard to investigate and prone to sampling error
high karma users aren’t that common either
the survey datasets are not huge: generally less than a thousand responses each
the datasets are heavily riddled with missingness: people didn’t answer a lot of questions. The usual stats program response is that if a particular subject is missing any of the variables looked at, it will be dropped entirely. So if we’re looking at a regression involving time-on-LW, probability-cryonics-will-work, and cryonics-something-or-other, from each survey we won’t get 1000 usable responses, we may have instead 300 complete-cases.
dichotomizing continuous variables (such as time & karma into veteran vs newbie, and cryonics status into signed-up vs not) loses information
percentages are not a good unit to work in, as linear regressions do not respect the range 0-100%, and the extremes get crushed (0.1 looks much the same as 0.001)
our analysis question is not exactly obvious: we are not interested in a simple test of difference, nor a regression of two independent variables (such as
glm(SignedUp ~ Karma + Probability, family=binomial)) but comparing two alternate models of the three variables, one model in which karma predicts both probability (-) and signed-up status (+) and probability predicts signed-up (+) as well, and a second model in which karma predicts probability (-) but only probability predicts signed-up status (+).these variables may have considerable measurement error in them: the total karma variable may reflect time-wasting as much as contributions, but using instead length of LW/OB involvement has a similar problem.
Some fixes for this:
1-3: we can scrape together as much data as possible by combining all the surveys together (200917ya, 201115ya, 201214ya, 201313ya, 201412ya; there was no 201016ya or 201511ya survey), dropping responses where they indicated they had answered a previous survey, and including a year variable to model heterogeneity
4: we can reduce missingness by the assumption of completely-missing-at-random and using a multiple-imputation package like MICE or any imputation options in our chosen library
5: we can avoid dichotomizing variables at all
6: the probability/percentages can be transformed into logit units, which will work much better in linear regressions.
7: the two competing models can be easily written down and compared using the generalization of linear models, structural equation models (SEM). We can then see which one fits better and quantify the relative Bayesian strength of the two models
8: we can pull in additional variables related to community participation and using them, karma, and length of involvement, extract a latent variable hopefully corresponding meaningfully to experience/veteranness; if we’re using a SEM package and can deal with missingness, this will be easier than it sounds.
Analysis
Data Preparation
PCryonics, KarmaScore, CryonicsStatus were asked every year and have not changed AFAIK. The community-related survey variables have changed from year to year, though, and matching up 2009–5201412ya variables we have available:
2009: OB.posts, Time.in.Community, Time.per.day
2011: Sequences, TimeinCommunity, TimeonLW, Meetups
2012: LessWrongUse, Sequences, TimeinCommunity, TimeonLW, Meetups, HPMOR
2013: Less.Wrong.Use, Sequences, TimeinCommunity, TimeonLW, Meetups, HPMOR
2014: LessWrongUse, Sequences, TimeinCommunity, TimeonLW, Meetups, HPMORLessWrongUse: consistentOB.posts=Sequences; both are %s, and the phrasing is consistent:OB.posts:What percentage of the Overcoming Bias posts do you think you’ve read? (Eliezer has about 700, and Robin probably around the same. If you’ve read all of Eliezer’s but none of Robin’s, or vice versa, please mention that in the answer)
Sequences:About how much of the Sequences - the collection of Eliezer Yudkowsky’s original posts - have you read? You can find a list of them at http://wiki.lesswrong.com/wiki/Sequences
TimeinCommunity: this variable turns out to be unusable, as reading through responses, the data is too dirty and inconsistent to be used at all without massive editing (everyone formatted their response differently, some didn’t understand the units, etc. Reminder to anyone running a survey: free response is the devil.)TimeonLW=Time.per.day: consistent, phrasing:Time.per.day:In an average day, how many minutes do you spend on Overcoming Bias and Less Wrong?
TimeonLW:How long, in approximate number of minutes, do you spend on Less Wrong in the average day?
Meetups; inconsistent:2009, 201115ya, 201214ya: True/False
2013, 201412ya: “Yes, regularly”/“Yes, once or a few times”/“No”
HPMOR: consistent
Reading in, merging, cleaning, and writing back out the survey data:
# 2009: https://www.lesswrong.com/posts/ZWC3n9c6v4s35rrZ3/survey-results
# https://docs.google.com/forms/d/1X-tr2qzvvHzWpRtZNeXHoeBr30uCms7SlMkhbCmuT4Q/viewform?formkey=cF9KNGNtbFJXQ1JKM0RqTkxQNUY3Y3c6MA
survey2009 <- read.csv("https://gwern.net/doc/lesswrong-survey/2009.csv", header=TRUE)
s2009 <- with(survey2009, data.frame(Year=2009, PCryonics=Probability..Cryonics, KarmaScore=LW.Karma, CryonicsStatus=Cryonics, Sequences=OB.posts, TimeonLW=Time.per.day))
s2009$Meetups <- NA; s2009$LessWrongUse <- NA; s2009$HPMOR <- NA
s2009$Year <- 2009
# 2011: https://www.lesswrong.com/posts/HAEPbGaMygJq8L59k/2011-survey-results
# https://docs.google.com/forms/d/1f2oOFHPjcWG4SoT57LsWkYsnNXgY1gkbISk4_FDQ3fc/viewform?formkey=dHlYUVBYU0Q5MjNpMzJ5TWJESWtPb1E6MQ
survey2011 <- read.csv("https://gwern.net/doc/lesswrong-survey/2011.csv", header=TRUE)
survey2011$KarmaScore <- survey2011$Karma # rename for consistency
## no 'PreviousSurveys' question asked, err on the side of inclusion
s2011 <- subset(survey2011, select=c(PCryonics, KarmaScore, CryonicsStatus, Sequences, TimeonLW, Meetups))
s2011$LessWrongUse <- NA; s2011$HPMOR <- NA
s2011$Year <- 2011
# 2012: https://www.lesswrong.com/posts/x9FNKTEt68Rz6wQ6P/2012-survey-results
# https://docs.google.com/spreadsheet/viewform?formkey=dG1pTzlrTnJ4eks3aE13Ni1lbV8yUkE6MQ#gid=0
survey2012 <- read.csv("https://gwern.net/doc/lesswrong-survey/2012.csv", header=TRUE)
s2012 <- subset(survey2012, PreviousSurveys!="Yes", select=c(PCryonics, KarmaScore, CryonicsStatus, LessWrongUse, Sequences, TimeonLW, Meetups, HPMOR))
s2012$Year <- 2012
# 2013: https://www.lesswrong.com/lw/jj0/2013_survey_results/
# https://docs.google.com/spreadsheet/viewform?usp=drive_web&formkey=dGZ6a1NfZ0V1SV9xdE1ma0pUMTc1S1E6MA#gid=0
survey2013 <- read.csv("https://gwern.net/doc/lesswrong-survey/2013.csv", header=TRUE)
survey2013$LessWrongUse <- survey2013$Less.Wrong.Use # rename for consistency
survey2013$PCryonics <- survey2013$P.Cryonics.
survey2013$KarmaScore <- survey2013$Karma.Score
survey2013$CryonicsStatus <- survey2013$Cryonics.Status
survey2013$TimeonLW <- survey2013$Time.on.LW
s2013 <- subset(survey2013, Previous.Surveys.1!="Yes", select=c(PCryonics, KarmaScore, CryonicsStatus, LessWrongUse, Sequences, TimeonLW, Meetups, HPMOR))
s2013$Year <- 2013
# 2014: https://www.lesswrong.com/lw/lhg/2014_survey_results/
# https://docs.google.com/forms/d/1h4IisKq7p8CRRVT_UXMSiKW6RE5U5nl1PLT_MvpbX2I/viewform
survey2014 <- read.csv("https://gwern.net/doc/lesswrong-survey/2014.csv", header=TRUE)
s2014 <- subset(survey2014, PreviousSurveys!="Yes", select=c(PCryonics, KarmaScore, CryonicsStatus, LessWrongUse, Sequences, TimeonLW, Meetups, HPMOR))
s2014$Year <- 2014
all <- rbind(s2009, s2011, s2012, s2013, s2014)
# Clean up:
all[!is.na(all$HPMOR) & (all$HPMOR == "" | all$HPMOR == " "),]$HPMOR <- NA
all[!is.na(all$HPMOR) & (all$HPMOR == "Yes all of it"),]$HPMOR <- "Yes, all of it"
all$HPMOR <- as.factor(all$HPMOR)
all$TimeonLW <- as.numeric(as.character(all$TimeonLW))
all$Meetups <- grepl("Yes", all$Meetups)
all[!is.na(all$TimeonLW) & all$TimeonLW>300,]$TimeonLW <- NA
Sequences <- regmatches(all$Sequences, regexec("[[:digit:]].", as.character(all$Sequences)))
all$Sequences <- as.integer(unlist({Sequences[sapply(Sequences, length)==0] <- NA; Sequences}))
all[!grepl("^I", all$LessWrongUse),]$LessWrongUse <- NA
all$LessWrongUse <- sub(",", "", all$LessWrongUse)
## PCryonics is *supposed* to be a percentage written down as a naked number, but some people include "%" as well or other text;
## so remove '%', convert to numeric, and then convert to decimal probability, rounding >100 down to 100 & <0 to 0
probabilityRange <- function(x) { if (is.na(x)) { return(NA);} else {if (x>100) { return(100); } else { if (x<0) { return(0); } else {return(x)}}}}
all$PCryonics <- sapply(as.numeric(sub("%", "", as.character(all$PCryonics))), probabilityRange) / 100
## Karma score relatively clean integer (note: can be negative but karma is integral & not real):
all$KarmaScore <- round(as.integer(as.character(all$KarmaScore)))
## CryonicsStatus has 14 levels and is tricky; first, code all the missing data
all[all$CryonicsStatus == "" | all$CryonicsStatus == " ",]$CryonicsStatus <- NA
# Done:
write.csv(all, file="~/wiki/doc/lesswrong-survey/2009-2015-cryonics.csv", row.names=FALSE)Analysis
First we need to load the data and convert the textual multiple-choice responses to ordinal factors which we can treat as numeric values:
cryonics <- read.csv("https://gwern.net/doc/lesswrong-survey/2009-2015-cryonics.csv",
colClasses=c("factor", "numeric", "numeric", "factor", "numeric", "numeric","logical","factor","factor"))
## now, express as ordinal, ranging from most extreme no to most extreme yes;
## so we can treat it as categorical, ordinal, or integer; we have to manually specify this metadata unless we want to drop down to
## integer-coding and delete the character responses, oh well.
cryonics$CryonicsStatus <- ordered(cryonics$CryonicsStatus,
levels=c("No, and don't plan to", "No, and not planning to", "No - and do not want to sign up for cryonics", "No", "Never thought about it / don't understand", "No, never thought about it", "No, but considering it", "No - still considering it", "No - would like to sign up but haven't gotten around to it","No - would like to sign up but unavailable in my area", "Yes - signed up or just finishing up paperwork", "Yes"))
cryonics$LessWrongUse <- ordered(cryonics$LessWrongUse,
levels=c("I lurk but never registered an account", "I've registered an account but never posted", "I've posted a comment but never a top-level post", "I've posted in Discussion but not Main", "I've posted in Main"))
cryonics$HPMOR <- ordered(cryonics$HPMOR,
levels=c("No", "Started it but haven't finished","Yes, all of it"))
summary(cryonics)
# Year PCryonics KarmaScore
# 2009: 153 Min. :0.0000000 Min. : -20.000
# 2011: 930 1st Qu.:0.0100000 1st Qu.: 0.000
# 2012: 649 Median :0.1000000 Median : 0.000
# 2013: 962 Mean :0.2129401 Mean : 192.535
# 2014:1226 3rd Qu.:0.3000000 3rd Qu.: 43.000
# Max. :1.0000000 Max. :15000.000
# NA's :565 NA's :1120
# CryonicsStatus Sequences
# No - still considering it :902 Min. : 0.00000
# No - and do not want to sign up for cryonics :610 1st Qu.:25.00000
# No, but considering it :594 Median :25.00000
# No - would like to sign up but haven't gotten around to it:393 Mean :41.75323
# No, and not planning to :330 3rd Qu.:50.00000
# (Other) :532 Max. :99.00000
# NA's :559 NA's :1598
# TimeonLW Meetups LessWrongUse
# Min. : 0.00000 Mode :logical I lurk but never registered an account :1071
# 1st Qu.: 5.00000 FALSE:3174 I've registered an account but never posted : 370
# Median : 10.00000 TRUE :746 I've posted a comment but never a top-level post: 611
# Mean : 16.27418 NA's :0 I've posted in Discussion but not Main : 233
# 3rd Qu.: 20.00000 I've posted in Main : 95
# Max. :300.00000 NA's :1540
# NA's :703
# HPMOR
# No : 516
# Started it but haven't finished: 319
# Yes, all of it :1018
# NA's :2067
total <- nrow(cryonics); total
# [1] 3920
full <- nrow(cryonics[!is.na(cryonics$PCryonics) & !is.na(cryonics$KarmaScore) & !is.na(cryonics$CryonicsStatus),]); full
full / total
# [1] 0.6420918367
cryonics$CryonicsStatusN <- as.integer(cryonics$CryonicsStatus)
cor(subset(cryonics, select=c(CryonicsStatusN, PCryonics, KarmaScore)), use="complete.obs")
# CryonicsStatusN PCryonics KarmaScore
# CryonicsStatusN 1.00000000000 0.27390817380 0.05904632281
# PCryonics 0.27390817380 1.00000000000 -0.04139505356
# KarmaScore 0.05904632281 -0.04139505356 1.00000000000So for the fundamental triplet of probability/karma/signup, we lose 36% of responses to missingness in one or more of the 3 variables. We can see in the complete cases the first-order correlations Yvain was spotting: karma has the predicted positive correlation with signup but the predicted negative correlation with probability. The size of the correlations are not impressive but we can guess why not: karma is heavily skewed (median 0, mean 192, max 15,000) and probability has a misleadingly narrow range (0-1), so one variable is grossly variable while the other is not variable enough.
To deal with the karma problem, we shift that -20 up to 0, and then we shrink them with a log-transform. This gives us a more comprehensible distribution 0-10. To deal with the probability, we want to do the opposite: expand them out so 0.99 is meaningfully smaller than 0.9999 etc., with a logit transform. The logit transform has a wrinkle: a lot of people (particularly those hostile to cryonics) are bad at probabilities and gave 0/1 values, which is unhelpful, so I round 0/1s; after that, the logit transform works nicely.
Now when we graph the triplet, our graph shows us something interesting:
cryonics$KarmaScoreLog <- log1p(cryonics$KarmaScore + abs(min(cryonics$KarmaScore, na.rm=TRUE)))
### 0 & 1 are not real subjective probabilities; truncate probabilities
cryonics[!is.na(cryonics$PCryonics) & cryonics$PCryonics<1e-15,]$PCryonics <- exp(-20)
cryonics[!is.na(cryonics$PCryonics) & cryonics$PCryonics==1,]$PCryonics <- exp(10)
### now that the probabilities are real, convert them into logits to avoid decimal's distortion of extremes
cryonics$PCryonicsLogit <- log(cryonics$PCryonics / (1 - cryonics$PCryonics))
## visualize
library(ggplot2)
qplot(KarmaScoreLog, jitter(PCryonicsLogit), color=CryonicsStatusN, data=cryonics,
ylab="Probability of cryonics working (logits)", xlab="LessWrong karma (logged)") + geom_point(size=I(3))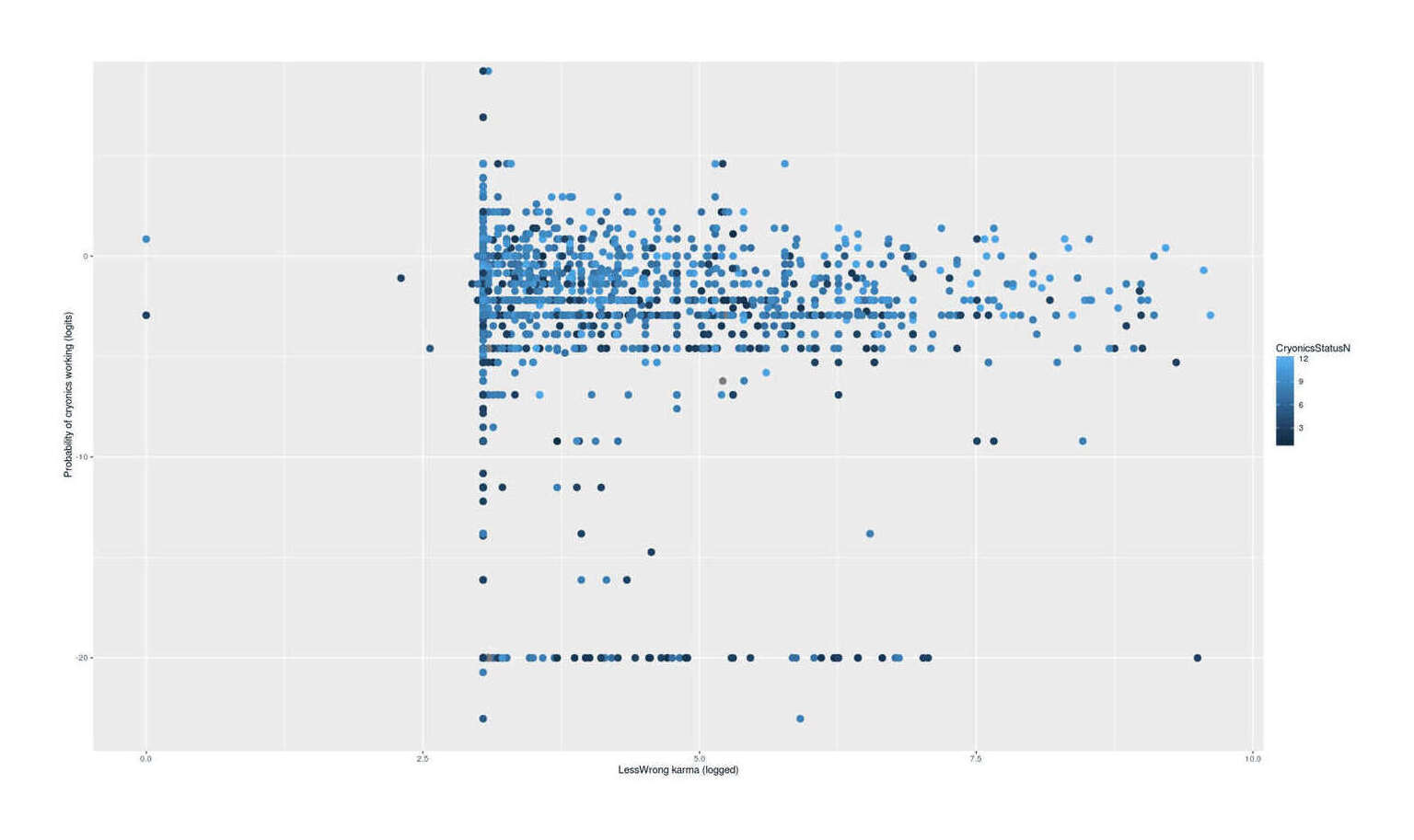
LW karma vs estimated probability of cryonics working vs degree to which one wants to sign up (2009–5201412ya LW survey data)
We see heteroscedasticity with a striking decrease in variance with karma / funnel shape, which looks as if with increasing LW karma, there is a convergence on a mean logit of ~2.5 or 12%. Such a convergence would be a strike against the idea that high-karma users sign up only because they are overconfident about cryonics - the heteroscedasticity should work in the other direction, then, with higher variance in the high karma users, permitting the low-probability & non-signup respondents to overcompensate for the high-probability & signup users. The data is not visually clear about whether among high karma users (say, 6+) a high probability predicts a higher signup variable; maybe it does, maybe it doesn’t, I can see it either way.
So to go back to our interpretations: we want to predict cryonics signup. We have 2 competing models: in one model, signup is influenced by probability
blavaan: prerequisites are not on CRAN but Bioconductor, so you need to do
source("http://bioconductor.org/biocLite.R"); biocLite(c("graph", "Rgraphviz"))
# turn ordered factors into integers, and Year into dummy variables (Year2009, Year2011, Year2012, Year2013, Year2014) because Blavaan isn't smart enough to do that on its own:
cryonicsExpanded <- with(cryonics, data.frame(model.matrix(~Year+0), CryonicsStatusN, KarmaScoreLog, PCryonicsLogit, Sequences, TimeonLW, Meetups, LessWrongUse, HPMOR))
cryonicsExpanded$Meetups <- as.integer(cryonicsExpanded$Meetups)
cryonicsExpanded$LessWrongUse <- as.integer(cryonicsExpanded$LessWrongUse)
cryonicsExpanded$HPMOR <- as.integer(cryonicsExpanded$HPMOR)
cryonicsExpanded$SequencesLog <- log(cryonicsExpanded$Sequences)
cryonicsExpanded$TimeonLWLog <- log1p(cryonicsExpanded$TimeonLW)
library(blavaan)
Cryonics.model1 <- '
PCryonicsLogit ~ KarmaScoreLog
CryonicsStatusN ~ PCryonicsLogit + KarmaScoreLog
'
b <- bsem(model = Cryonics.model1, data = na.omit(cryonicsExpanded[,1:8]), dp=dpriors(beta="dnorm(0,1e-1)", nu = "dnorm(0,1e-2)")); summary(b)
l <- bsem(model = Cryonics.model1, data = na.omit(cryonicsExpanded[,1:8])); summary(l)
Cryonics.model.latent <- '
Experience =~ KarmaScoreLog + SequencesLog + TimeonLWLog + Meetups + LessWrongUse + HPMOR
PCryonicsLogit ~ Experience
CryonicsStatusN ~ PCryonicsLogit + Experience
'
blat <- bsem(model = Cryonics.model.latent, data = na.omit(cryonicsExpanded), dp=dpriors(beta="dnorm(0,1e-1)", nu = "dnorm(0,1e-2)")); summary(blat)
semPaths(llat,"est", edge.label.cex = 0.5, exoVar = FALSE, exoCov = FALSE, nCharNodes=10, layout="tree2", sizeMan=10, sizeMan2=10, residuals=FALSE, label.prop=5, edge.label.cex=1.3, mar=c(1.5,1.5,1.5,1.5))
Cryonics.fit1.cb <- bsem(model = Cryonics.model1.c, data = na.omit(cryonicsExpanded[,1:8]), jagcontrol=list(method="rjparallel")); Cryonics.fit2.cb <- bsem(model = Cryonics.model2.c, data = na.omit(cryonicsExpanded[,1:8]), jagcontrol=list(method="rjparallel")); BF(Cryonics.fit1.cb, Cryonics.fit2.cb)## turn Year into dummy variables (Year2009, Year2011, Year2012, Year2013, Year2014) because Lavaan isn't smart enough to do that on its own:
cryonics <- with(cryonics, data.frame(model.matrix(~Year+0), CryonicsStatusN, KarmaScoreLog, PCryonicsLogit, CryonicsStatusPbroad, CryonicsStatusPnarrow, Sequences, TimeonLW, Meetups, LessWrongUse, HPMOR))
library(lavaan)
## the two models, continuous/ordinal response to cryonics status:
Cryonics.model1.c <- '
PCryonicsLogit ~ KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusN ~ PCryonicsLogit + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit1.c <- sem(model = Cryonics.model1.c, missing="fiml", data = cryonics)
summary(Cryonics.fit1.c)
Cryonics.model2.c <- '
PCryonicsLogit ~ KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusN ~ PCryonicsLogit + KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit2.c <- sem(model = Cryonics.model2.c, missing="fiml", data = cryonicsExpanded)
summary(Cryonics.fit2.c)
anova(Cryonics.fit1.c, Cryonics.fit2.c)
## broad dichotomization:
cryonics$CryonicsStatusPbroad <- as.integer(cryonics$CryonicsStatusPbroad)
Cryonics.model1.d.b <- '
PCryonicsLogit ~ KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusPbroad ~ PCryonicsLogit + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit1.d.b <- sem(model = Cryonics.model1.d.b, link="logit", missing="fiml", data = cryonics)
summary(Cryonics.fit1.d.b)
Cryonics.model2.d.b <- '
PCryonicsLogit ~ KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusPbroad ~ PCryonicsLogit + KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit2.d.b <- sem(model = Cryonics.model2.d.b, link="logit", missing="fiml", data = cryonics)
summary(Cryonics.fit2.d.b)
anova(Cryonics.fit1.d.b, Cryonics.fit2.d.b)
## narrow dichotomization:
Cryonics.model1.d.n <- '
PCryonicsLogit ~ KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusPnarrow ~ PCryonicsLogit + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit1.d.n <- sem(model = Cryonics.model1.d.n, link="logit", missing="fiml", data = cryonics)
summary(Cryonics.fit1.d.n)
Cryonics.model2.d.n <- '
PCryonicsLogit ~ KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusPnarrow ~ PCryonicsLogit + KarmaScoreLog + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit2.d.n <- sem(model = Cryonics.model2.d.n, link="logit", missing="fiml", data = cryonics)
summary(Cryonics.fit2.d.n)
anova(Cryonics.fit1.d.n, Cryonics.fit2.d.n)
cryonics$LessWrongUse <- as.integer(cryonics$LessWrongUse)
cryonics$HPMOR <- as.integer(cryonics$HPMOR)
Cryonics.model3.d.n <- '
Experience =~ KarmaScoreLog + Sequences + TimeonLW + Meetups + LessWrongUse + HPMOR + Year2009 + Year2011 + Year2012 + Year2013
PCryonicsLogit ~ Experience + Year2009 + Year2011 + Year2012 + Year2013
CryonicsStatusPnarrow ~ PCryonicsLogit + Experience + Year2009 + Year2011 + Year2012 + Year2013
'
Cryonics.fit3.d.n <- sem(model = Cryonics.model3.d.n, link="logit", missing="fiml", data = cryonics)
summary(Cryonics.fit3.d.n)TODO:
age, degree, physics specialty? http://slatestarscratchpad.tumblr.com/post/114103150216/su3su2u1-i-was-more-referring-to-the-further http://slatestarscratchpad.tumblr.com/post/114100766461/su3su2u1-slatestarscratchpad-when-i-defined http://slatestarscratchpad.tumblr.com/post/114097328806/thinkingornot-su3su2u1-thinkingornot-maybe-you (can steal degree unfolding from EA donations)