---
title: How Often Does Correlation=Causality?
description: Compilation of studies comparing observational results with randomized experimental results on the same intervention, compiled from medicine/economics/psychology, indicating that a large fraction of the time (although probably not a majority) correlation ≠ causality.
thumbnail: /doc/psychology/cognitive-bias/2018-jones-table5-nyt-randomizedvscorrelation.png
thumbnail-text: "Graph illustrating that correlational estimates can vastly overestimate causal statistical estimates due to pervasive confounding; in this case, of exercise programs and health."
thumbnail-css: "outline"
created: 2014-06-24
modified: 2022-06-14
status: in progress
previous: /everything
next: /doc/sociology/1987-rossi
importance: 10
css-extension: dropcaps-kanzlei
...
# Medical
["How study design affects outcomes in comparisons of therapy. I: Medical"](https://www.ime.usp.br/~abe/lista/pdfpWvyXNv25a.pdf), Colditz et al 1989:
> We analysed 113 reports published in 1980 in a sample of medical journals to relate features of study design to the magnitude of gains attributed to new therapies over old. Overall we rated 87% of new therapies as improvements over standard therapies. The mean gain (measured by the Mann-Whitney statistic) was relatively constant across study designs, except for non-randomized controlled trials with sequential assignment to therapy, which showed a significantly higher likelihood that a patient would do better on the innovation than on standard therapy (_p_ = 0.004). Randomized controlled trials that did not use a double- blind design had a higher likelihood of showing a gain for the innovation than did double-blind trials (_p_ = 0.02). Any evaluation of an innovation may include both bias and the true efficacy of the new therapy, therefore we may consider making adjustments for the average bias associated with a study design. When interpreting an evaluation of a new therapy, readers should consider the impact of the following average adjustments to the Mann-Whitney statistic: for trials with non-random sequential assignment a decrease of 0.15, for non-double-blind randomized controlled trials a decrease of 0.11.
["How study design affects outcomes in comparisons of therapy. II: Surgical"](https://www.ime.usp.br/~abe/lista/pdfSDs9TvkeEz.pdf), Miller et al 1989:
> We analysed the results of 221 comparisons of an innovation with a standard treatment in surgery published in 6 leading surgery journals in 1983 to relate features of study design to the magnitude of gain. For each comparison we measured the gain attributed to the innovation over the standard therapy by the Mann-Whitney statistic and the difference in proportion of treatment successes. For primary treatments (aimed at curing or ameliorating a patient's principal disease), an average gain of 0.56 was produced by 20 randomized controlled trials. This was less than the 0.62 average for four non-randomized controlled trials, 0.63 for 19 externally controlled trials, and 0.57 for 73 record reviews (0.50 represents a toss-up between innovation and standard). For secondary therapies (used to prevent or treat complications of therapy), the average gain was 0.53 for 61 randomized controlled trials, 0.58 for eleven non-randomized controlled trials, 0.54 for eight externally controlled trials, and 0.55 for 18 record reviews.
["Developing improved observational methods for evaluating therapeutic effectiveness"](/doc/statistics/causality/1990-horwitz.pdf), Horwitz et al 1990:
> ...The specific topic investigated was the prophylactic effectiveness of β-blocker therapy after an acute myocardial infarction. To accomplish the research objective, three sets of data were compared. First, we developed a restricted cohort based on the eligibility criteria of the randomized clinical trial; second, we assembled an expanded cohort using the same design principles except for not restricting patient eligibility; and third, we used the data from the Beta Blocker Heart Attack Trial (BHAT), whose results served as the gold standard for comparison. In this research, the treatment difference in death rates for the restricted cohort and the BHAT trial was nearly identical. In contrast, the expanded cohort had a larger treatment difference than was observed in the BHAT trial. We also noted the important and largely neglected role that eligibility criteria may play in ensuring the validity of treatment comparisons and study outcomes....
["Choosing between randomized and non-randomised studies: a systematic review"](/doc/statistics/causality/1998-britton.pdf "'Choosing Between Randomized and Non-randomised Studies', Britton et al 1998"), Britton et al 1998 ([summary](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1126943/ "'Interpreting the evidence: choosing between randomized and non-randomised studies', McKee et al 1999")):
> This review explored those issues related to the process of randomization that may affect the validity of conclusions drawn from the results of RCTs and non-randomised studies.
> ...Previous comparisons of RCTs and non-randomised studies: 18 papers that directly compared the results of RCTs and prospective non-randomised studies were found and analysed. No obvious patterns emerged; neither the RCTs nor the non-randomised studies consistently gave larger or smaller estimates of the treatment effect. The type of intervention did not appear to be influential, though more comparisons need to be conducted before definite conclusions can be drawn.
>
> 7 of the 18 papers found no [statistically-]significant differences between treatment effects from the two types of study. 5 of these 7 had adjusted results in the non-randomised studies for baseline prognostic differences. The remaining 11 papers reported [statistically-significant] differences which are summarised in Table 3.
>
> 7 studies obtained differences in the same direction but of significantly different magnitude. In 3, effect sizes were greater in the RCTs.
>
> ...However, the evidence reviewed here is extremely limited. It suggests that adjustment for baseline differences in arms of non-randomised studies will not necessarily result in similar effect sizes to those obtained from RCTs.
["Spurious precision? Meta-analysis of observational studies"](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2665367/pdf/9462324.pdf), Egger et al 1998:
> Meta-analysis of observational studies is as common as meta-analysis of controlled trials Confounding and selection bias often distort the findings from observational studies There is a danger that meta-analyses of observational data produce very precise but equally spurious results The statistical combination of data should therefore not be a prominent component of reviews of observational studies More is gained by carefully examining possible sources of heterogeneity between the results from observational studies Reviews of any type of research and data should use a systematic approach, which is documented in a materials and methods section.
>
> ...The randomized controlled trial is the principal research design in the evaluation of medical interventions. However, aetiological hypotheses - for example, those relating common exposures to the occurrence of disease - cannot generally be tested in randomized experiments. Does breathing other people's tobacco smoke cause lung cancer, drinking coffee cause coronary heart disease, and eating a diet rich in saturated fat cause breast cancer? Studies of such "menaces of daily life"^6^ use observational designs or examine the presumed biological mechanisms in the laboratory. In these situations the risks involved are generally small, but once a large proportion of the population is exposed, the potential public health implications of these associations - if they are causal - can be striking.
>
> ...If years later established interventions are incriminated with adverse effects, there will be ethical, political, and legal obstacles to the conduct of a new trial. Recent examples for such situations include the controversy surrounding a possible association between intramuscular administration of vitamin K to newborns and the risk of childhood cancer^8^ and whether oral contraceptives increase women's risk of breast cancer.^9^
>
> ...Patients exposed to the factor under investigation may differ in several other aspects that are relevant to the risk of developing the disease in question. Consider, for example, smoking as a risk factor for suicide. Virtually all cohort studies have shown a positive association, with a dose-response relation being evident between the amount smoked and the probability of committing suicide.^14-19^ Figure 1 illustrates this for four prospective studies of middle aged men, including the massive cohort of patients screened for the multiple risk factors intervention trial. Based on over 390 000 men and almost five million years of follow up, a meta-analysis of these cohorts produces highly precise and significant estimates of the increase in suicide risk that is associated with smoking different daily amounts of cigarettes: relative rate for 1-14 cigarettes 1.43 (95% confidence interval 1.06 to 1.93), for 15-24 cigarettes 1.88 (1.53 to 2.32), >25 cigarettes 2.18 (1.82 to 2.61). On the basis of established criteria,^20^ many would consider the association to be causal - if only it were more plausible. Indeed, it is improbable that smoking is causally related to suicide.^14^ Rather, it is the social and mental states predisposing to suicide that are also associated with the habit of smoking.
>
> ...Beta carotene has antioxidant properties and could thus plausibly be expected to prevent carcinogenesis and atherogenesis by reducing oxidative damage to DNA and lipoproteins.^27^ Contrary to many other associations found in observational studies, this hypothesis could be, and was, tested in experimental studies. The findings of four large trials have recently been published.^28-31^ The results were disappointing and even - for the two trials conducted in men at high risk (smokers and workers exposed to asbestos)^28,29^ - disturbing. ...With a fixed effects model, the meta-analysis of the cohort studies shows a significantly lower risk of cardiovascular death (relative risk reduction 31% (95% confidence interval 41% to 20%, _p_ < 0.0001)) (fig 2). The results from the randomized trials, however, show a moderate adverse effect of â-carotene supplementation (relative increase in the risk of cardiovascular death 12% (4% to 22%, _p_ = 0.005)). Similarly discrepant results between epidemiological studies and trials were observed for the incidence of and mortality from cancer. ...Fig 2 Meta-analysis of association between Beta-carotene intake and cardiovascular mortality: results from observational studies show considerable benefit, whereas the findings from randomized controlled trials show an increase in the risk of death. Meta-analysis is by fixed effects model.
>
> ...However, even if adjustments for confounding factors have been made in the analysis, [residual confounding](/note/regression "'Regression To The Mean Fallacies', Branwen 2021") remains a potentially serious problem in observational research. Residual confounding arises when a confounding factor cannot be measured with sufficient precision-which often occurs in epidemiological studies.^22,23^
>
> ...Implausibility of results, as in the case of smoking and suicide, rarely protects us from reaching misleading claims. It is generally easy to produce plausible explanations for the findings from observational research. In a cohort study of sex workers, for example, one group of researchers that investigated cofactors in transmission of HIV among heterosexual men and women found a strong association between oral contraceptives and HIV infection, which was independent of other factors.^25^ The authors hypothesised that, among other mechanisms, the risk of transmission could be increased with oral contraceptives due to "effects on the genital mucosa, such as increasing the area of ectopy and the potential for mucosal disruption during intercourse." In a cross sectional study another group produced diametrically opposed findings, indicating that oral contraceptives protect against the virus.^26^ This was considered to be equally plausible, "since progesterone-containing oral contraceptives thicken cervical mucus, which might be expected to hamper the entry of HIV into the uterine cavity." It is likely that confounding and bias had a role in producing these contradictory findings. This example should be kept in mind when assessing other seemingly plausible epidemiological associations.
>
> ...Several such situations are depicted in figure 3. Consider diet and breast cancer. The hypothesis from ecological analyses^33^ that higher intake of saturated fat could increase the risk of breast cancer generated much observational research, often with contradictory results. A comprehensive meta-analysis 34 showed an association for case-control but not for cohort studies (odds ratio 1.36 for case-control studies versus relative rate 0.95 for cohort studies comparing highest with lowest category of saturated fat intake, _p_ = 0.0002 for difference in our calculation) (fig 2). This discrepancy was also shown in two separate large collaborative pooled analyses of cohort and case-control studies.^35,36^
>
> The most likely explanation for this situation is that biases in the recall of dietary items and in the selection of study participants have produced a spurious association in the case-control comparisons.^36^ That differential recall of past exposures may introduce bias is also evident from a meta-analysis of case-control studies of intermittent sunlight exposure and melanoma (fig 3).^37^ When studies were combined in which some degree of blinding to the study hypothesis was achieved, only a small and non-statistically-significant effect (odds ratio 1.17 (95% confidence interval 0.98 to 1.39)) was evident. Conversely, in studies without blinding, the effect was considerably greater and significant (1.84 (1.52 to 2.25)). The difference between these two estimates is unlikely to be a product of chance (_p_ = 0.0004 in our calculation).
>
> The importance of the methods used for assessing exposure is further illustrated by a meta-analysis of cross sectional data of dietary calcium intake and blood pressure from 23 different studies.^38^ As shown in figure 3, the regression slope describing the change in systolic blood pressure (in mm Hg) per 100 mg of calcium intake is strongly influenced by the approach used for assessing the amount of calcium consumed. The association is small and only marginally significant with diet histories (slope −0.01 (−0.003 to −0.016)) but large and highly significant when food frequency questionnaires were used (−0.15 (−0.11 to −0.19)). With studies using 24 hour recall an intermediate result emerges (−0.06 (−0.09 to −0.03)). Diet histories assess patterns of usual intake over long periods of time and require an extensive interview with a nutritionist, whereas 24 hour recall and food frequency questionnaires are simpler methods that reflect current consumption.^39^ It is conceivable that different precision in the assessment of current calcium intake may explain the differences in the strength of the associations found, a statistical phenomenon known as regression dilution bias.^40^
>
> An important criterion supporting causality of associations is a dose-response relation. In occupational epidemiology the quest to show such an association can lead to very different groups of employees being compared. In a meta-analysis that examined the link between exposure to formaldehyde and cancer, funeral directors and embalmers (high exposure) were compared with anatomists and pathologists (intermediate to high exposure) and with industrial workers (low to high exposure, depending on job assignment).^41^ As shown in figure 3, there is a striking deficit of deaths from lung cancer among anatomists and pathologists (standardised mortality ratio 33 (95% confidence interval 22 to 47)), which is most likely to be due to a lower prevalence of smoking among this group. In this situation few would argue that formaldehyde protects against lung cancer. In other instances, however, such selection bias may be less obvious.
["Evaluating non-randomised intervention studies"](https://njl-admin.nihr.ac.uk/document/download/2004687), Deeks et al 2003:
> In the systematic reviews, eight studies compared results of randomized and non-randomised studies across multiple interventions using metaepidemiological techniques. A total of 194 tools were identified that could be or had been used to assess non-randomised studies. Sixty tools covered at least five of six pre-specified internal validity domains. Fourteen tools covered three of four core items of particular importance for non-randomised studies. Six tools were thought suitable for use in systematic reviews. Of 511 systematic reviews that included nonrandomised studies, only 169 (33%) assessed study quality. Sixty-nine reviews investigated the impact of quality on study results in a quantitative manner. The new empirical studies estimated the bias associated with non-random allocation and found that the bias could lead to consistent over- or underestimations of treatment effects, also the bias increased variation in results for both historical and concurrent controls, owing to haphazard differences in case-mix between groups. The biases were large enough to lead studies falsely to conclude significant findings of benefit or harm.
>
> ...Conclusion: Results of non-randomised studies sometimes, but not always, differ from results of randomized studies of the same intervention. Nonrandomised studies may still give seriously misleading results when treated and control groups appear similar in key prognostic factors. Standard methods of case-mix adjustment do not guarantee removal of bias. [Residual confounding](/note/regression "'Regression To The Mean Fallacies', Branwen 2021"){#gwern-notes-regression-2} may be high even when good prognostic data are available, and in some situations adjusted results may appear more biased than unadjusted results.
>
> Method:
>
> 1. Three reviews were conducted to consider:
>
> - empirical evidence of bias associated with non-randomised studies
> - the content of quality assessment tools for non-randomised studies
> - the use of quality assessment in systematic reviews of non-randomised studies.
>
> These reviews were conducted systematically, identifying relevant literature through comprehensive searches across electronic databases, hand-searches and contact with experts.
> 2. New empirical investigations were conducted generating non-randomised studies from two large, multi-centre RCTs by selectively resampling trial participants according to allocated treatment, centre and period. These were used to examine:
>
> - systematic bias introduced by the use of historical and non-randomised concurrent controls
> - whether results of non-randomised studies are more variable than results of RCTs
> - the ability of case-mix adjustment methods to correct for selection bias introduced by nonrandom allocation.
>
> The resampling design overcame particular problems of meta-confounding and variability of direction and magnitude of bias that hinder the interpretation of previous reviews.
>
> The first systematic review looks at existing evidence of bias in non-randomised studies, critically evaluating previous methodological studies that have attempted to estimate and characterise differences in results between RCTs and non-randomised studies.
> Two further systematic reviews focus on the issue of quality assessment of non-randomised studies. The first identifies and evaluates tools that can be used to assess the quality of non-randomised studies. The second looks at ways that study quality has been assessed and addressed in systematic reviews of healthcare interventions that have included non-randomised studies.
> The two empirical investigations focus on the issue of selection bias in non-randomised studies. The first investigates the size and behavior of selection bias in evaluations of two specific clinical interventions and the second assesses the degree to which case-mix adjustment corrects for selection bias.
>
> Evidence about the importance of design features of RCTs has accumulated rapidly during recent years.^19-21^ This evidence has mainly been obtained by a method of investigation that has been termed meta-epidemiology, a powerful but simple technique of investigating variations in the results of RCTs of the same intervention according to features of their study design.^22^ The process involves first identifying substantial numbers of systematic reviews each containing RCTs both with and without the design feature of interest. Within each review, results are compared between the trials meeting and not meeting each design criterion. These comparisons are then aggregated across the reviews in a grand overall meta-analysis to obtain an estimate of the systematic bias removed by the design feature. For RCTs, the relative importance of proper randomization, concealment of allocation and blinding have all been estimated using this technique.^20,21^ The results have been shown to be consistent across clinical fields,^23^ providing some evidence that meta-epidemiology may be a reliable investigative technique. The method has also been applied to investigate sources of bias in studies of diagnostic accuracy, where participant selection, independent testing and use of consistent reference standards have been identified as being the most important design features.^24^
>
> 8 reviews were identified which fulfilled the inclusion criteria; seven considered medical interventions and one psychological interventions. Brief descriptions of the methods and findings of each review are given below, with summary details given in Table 2. There is substantial overlap in the interventions (and hence studies) that were included in the reviews of medical interventions (Table 3):
>
> - Sacks et al 1982, ["Randomized versus historical controls for clinical trials"](/doc/statistics/causality/1982-sacks.pdf):
>
> Sacks and colleagues compared the results of RCTs with historically controlled trials (HCTs). The studies were identified in Chalmers' personal collection of RCTs, HCTs and uncontrolled studies maintained since 1955 by searches of Index Medicus, Current Contents and references of reviews and papers in areas of particular medical interest (full list not stated). Six interventions were included for which at least two RCTs and two HCTs were identified [cirrhosis with oesophageal varices, coronary artery surgery, anticoagulants for acute myocardial infarction, 5-fluorouracil adjuvant therapy for colon cancer, bacille Calmette-Guérin vaccine (BCG) adjuvant immunotherapy and diethylstilbestrol for habitual abortion (Table 3)]. Trial results were classified as positive if there was either a statistically-significant benefit or if the authors concluded benefit in the absence of statistical analysis, otherwise as negative. For each of the six interventions, a higher percentage of HCTs compared with RCTs concluded benefit: across all six interventions 20% of RCTs showed benefit compared with 79% of the HCTs.
> - Kunz and Oxman [Kunz & Oxman 1998, ["The unpredictability paradox: review of empirical comparisons of randomized and non-randomised clinical trials"](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC28700/)] and Kunz, Vist and Oxman [Kunz et al 2002/2008, ["Randomisation to protect against selection bias in healthcare trials (Cochrane Methodology Review)"](https://www.jameslindlibrary.org/wp-data/uploads/2014/05/Kunz-et-al-2002.pdf)]:
>
> Kunz and Oxman searched the literature for reviews that made empirical comparisons between the results of randomized and non-randomised studies. They included the results of the six comparisons in Sacks and colleagues' study above, and results from a further five published comparisons [antiarrhthymic therapy for atrial fibrillation, allogenic leucocyte immunotherapy for recurrent miscarriage, contrast media for salpingography, hormonal therapy for cryptorchidism, and transcutaneous electrical nerve stimulation (TENS) for postoperative pain (Table 3)].
> In some of the comparisons, RCTs were compared with truly observational studies and, in others they were compared with quasi-experimental trials. A separate publication of anticoagulants for acute myocardial infarction already included in Sacks and colleagues' review was also reviewed,^30^ as was a comparison of differences in control group event rates between randomized and non-randomised studies for treatments for six cancers (which does not fit within our inclusion criteria).^31^ The review was updated in 2002 including a further 11 comparisons, and published as a Cochrane methodology review.^29^
> The results of each empirical evaluation were described, but no overall quantitative synthesis was carried out. The results showed differences between RCTs and non-randomised studies in 15 of the 23 comparisons, but with inconsistency in the direction and magnitude of the difference. It was noted that non-randomised studies overestimated more often than they underestimated treatment effects.
> ...In 15 of 23 comparisons effects were larger in non-randomised studies, 4 studies had comparable results, whilst 4 reported smaller effects
> - Britton, McKee, Black, McPherson, Sanderson and Bain 25 [Britton et al 1998, ["Choosing between randomized and non-randomised studies: a systematic review"](/doc/statistics/causality/1998-britton.pdf "'Choosing Between Randomized and Non-randomised Studies', Britton et al 1998")]:
>
> Britton and colleagues searched for primary publications that made comparisons between single randomized and non-randomised studies (14 comparisons) and secondary publications (reviews) making similar comparisons (four comparisons). Both observational and quasiexperimental studies were included in the nonrandomised category. They included all four of the secondary comparisons included in the review by Kunz and colleagues^28^ (Table 3). The single study comparisons included studies where a comparison was made between participants who were allocated to experimental treatment as part of a trial and a group who declined to participate, and studies of centres where simultaneous randomized and patient-preference studies had been undertaken of the same intervention. The studies were assessed to ensure that the randomized and nonrandomised studies were comparable on several dimensions (Table 4).
> There were statistically-significant differences between randomized and non-randomised studies for 11 of the 18 comparisons. The direction of these differences was inconsistent and the magnitude extremely variable. For some interventions the differences were very large. For example, in a review of treatments for acute non-lymphatic leukaemia, the risk ratio in RCTs was 24 compared with 3.7 in non-randomised studies (comparison 23 in Table 3).
> The impact of statistical adjustment for baseline imbalances in prognostic factors was investigated in two primary studies, and in four additional comparisons (coronary angioplasty versus bypass grafting, calcium antagonists for cardiovascular disease, malaria vaccines and stroke unit care: comparisons 25-28 in Table 3). In two of the six comparisons there was evidence that adjustment for prognostic factors led to improved concordance of results between randomized and non-randomised studies.
> - MacLehose, Reeves, Harvey, Sheldon, Russell and Black^26^ [MacLehose et al 2000, ["A systematic review of comparisons of effect sizes derived from randomized and non-randomised studies"](/doc/statistics/causality/2000-maclehose.pdf "'Study design and estimates of effectiveness', MacLehose et al 2000")]:
>
> MacLehose and colleagues restricted their review to studies where results of randomized and nonrandomised comparisons were reported together in a single paper, arguing that such comparisons are more likely to be of 'like-with-like' than those made between studies reported in separate papers. They included primary studies and also reviews that pooled results from several individual studies. Of the 14 comparisons included in their report, three were based on reviews (comparisons 3, 7 and 25 in Table 3) and the rest were results from comparisons within single studies. The nonrandomised designs included comprehensive cohort studies, other observational studies and quasi-experimental designs.
> The 'fairness' or 'quality' of each of the comparisons made was assessed for comparability of patients, interventions and outcomes and additional study methodology (see Table 4). Although the authors did not categorise comparisons as showing equivalence or discrepancy, the differences in results were found to be significantly greater in comparisons ranked as being low quality.
> ...In 14 of 35 comparisons the discrepancy in RR was <10%, in 5 comparisons it was >50%. Discrepancies were smaller in "fairer" comparisons.
> - Benson and Hartz^32^ [Benson & Hartz 2000, ["A comparison of observational studies and randomized, controlled trials"](https://www.nejm.org/doi/full/10.1056/NEJM200006223422506)]:
>
> Benson and Hartz evaluated 19 treatment comparisons (eight in common with Britton and colleagues^25^) for which they located at least one randomized and one observational study (defined as being a study where the treatment was not allocated for the purpose of research) in a search of MEDLINE and the databases in the Cochrane Library (Table 4). They only considered treatments administered by physicians. Across the 19 comparisons they found 53 observational and 83 randomized studies, the results of which were meta-analysed separately for each treatment comparison. Comparisons were made between the pooled estimates, noting whether the point estimate from the combined observational studies was within the confidence interval of the RCTs. They found only two instances where the observational and randomized studies did not meet this criterion.
> - Concato, Shah and Horwitz^33^ [Concato et al 2000, ["Randomized, Controlled Trials, Observational Studies, and the Hierarchy of Research Designs"](https://www.nejm.org/doi/full/10.1056/nejm200006223422507)]:
>
> Concato and colleagues searched for meta-analyses of RCTs and of observational studies (restricted to case-control and concurrent cohort studies) published in five leading general medical journals. They found only five comparisons where both types of study had been meta-analysed [BCG vaccination for tuberculosis (TB), mammographic screening for breast cancer mortality, cholesterol levels and death from trauma, treatment of hypertension and stroke, treatment of hypertension and coronary heart disease (CHD) (Table 3)] combining a total of 55 randomized and 44 observational studies. They tabulated the results of meta-analyses of the randomized and the observational studies and considered the similarity of the point estimates and the range of findings from the individual studies. In all five instances they noted the pooled results of randomized and non-randomised studies to be similar. Where individual study results were available, the range of the RCT results was greater than the range of the observational results.
>
> [[Pocock & Elbourne criticism](https://edisciplinas.usp.br/pluginfile.php/338043/mod_folder/content/0/CR%C3%8DTICA/pocock_nejm_2000.pdf?forcedownload=1) of Benson and Concato studies.]
> - Ioannidis, Haidich, Pappa, Pantazis, Kokori, Tektonidou, Contopoulous-Ioannidis and Lau^34^ \[[Ioannidis et al 2001](#ioannidis-et-al-2001)\]:
>
> Ioannidis and colleagues searched for reviews that considered results of RCTs and non-randomised studies. In addition to searching MEDLINE they included systematic reviews published in the Cochrane Library, locating in total 45 comparisons. Comparisons of RCTs with both quasi-randomised and observational studies were included. All meta-analytical results were expressed as odds ratios, and differences between randomized and non-randomised results expressed as a ratio of odds ratios and their statistical-significance calculated. Findings across the 45 topic areas were pooled incorporating results from 240 RCTs and 168 non-randomised studies. Larger treatment effects were noted more often in non-randomised studies. In 15 cases (33%) there was at least a twofold variation in odds ratios, whereas in 16% there were statistically-significant differences between the results of randomized and non-randomised studies. The authors also tested the heterogeneity of the results of the randomized and non-randomised studies for each topic. Significant heterogeneity was noted for 23% of the reviews of RCTs and for 41% of the reviews of non-randomised studies.
> - Lipsey and Wilson^35^ \[Lipsey & Wilson 1993, ["The efficacy of psychological, educational, and behavioral treatment: Confirmation from meta-analysis"](/doc/psychology/1993-lipsey.pdf "'The Efficacy of Psychological, Educational, and Behavioral Treatment: Confirmation from Meta-Analysis', Lipsey & Wilson 1993"){#lipsey-wilson-1993-1}\] and Wilson and Lipsey \[Wilson & Lipsey 2001, ["The role of method in treatment effectiveness research: evidence from meta-analysis"](/doc/statistics/causality/2001-wilson.pdf)\]^36^:
>
> Lipsey and Wilson searched for all meta-analyses of psychological interventions, broadly defined as treatments whose intention was to induce psychological change (whether emotional, attitudinal, cognitive or behavioural). Evaluations of individual components of interventions and broad interventional policies or organisational arrangements were excluded. Searches of psychology and sociology databases supported by manual searches identified a total of 302 meta-analyses, 76 of which contained both randomized and non-randomised comparative studies. Results were analysed in two ways. First, the average effect sizes of randomized and non-randomised studies were computed across the 74 reviews, and average effects were noted to be very slightly smaller for non-randomised than randomized studies. Second (and more usefully) the difference in effect sizes between randomized and non-randomised studies within each of the reviews was computed and plotted. This revealed both large over- and underestimates with non-randomised studies, differences in effect sizes ranging from -0.60 to +0.77 standard deviations.
>
> Three commonly cited studies were excluded from our review.^37-39^ Although these studies made comparisons between the results of randomized and non-randomised studies across many interventions, they did not match RCTs and nonrandomised studies according to the intervention. Although they provide some information about the average findings of selected randomized and nonrandomised studies, they did not consider whether there are differences in results of RCTs and nonrandomised studies of the same intervention.
>
> *Findings of the eight reviews*: The eight reviews have drawn conflicting conclusions. 5 of the eight reviews concluded that there are differences between the results of randomized and non-randomised studies in many but not all clinical areas, but without there being a consistent pattern indicating systematic bias.^25,26,28,34,35^ One of the eight reviews found an overestimation of effects in all areas studied.^27^ The final two concluded that the results of randomized and non-randomised studies were 'remarkably similar'.^32,33^ Of the two reviews that considered the relative variability of randomized and non-randomised results, one concluded that RCTs were more consistent^34^ and the other that they were less consistent.^33^
["Contradicted and Initially Stronger Effects in Highly Cited Clinical Research"](https://jamanetwork.com/journals/jama/fullarticle/201218), Ioannidis 2005
:
> 5 of 6 highly-cited nonrandomized studies had been contradicted or had found stronger effects vs 9 of 39 randomized controlled trials (p = 0.008)...Matched control studies did not have a significantly different share of refuted results than highly cited studies, but they included more studies with "negative" results...Similarly, there is some evidence on disagreements between epidemiological studies and randomized trials.^3-5^
>
> ...For highly cited nonrandomized studies, subsequently published pertinent randomized trials and meta-analyses thereof were eligible regardless of sample size; nonrandomized evidence was also considered, if randomized trials were not available...5 of 6 highly cited nonrandomized studies had been contradicted or had initially stronger effects while this was seen in only 9 of 39 highly cited randomized trials (p = 0.008). Table 3 shows that trials with contradicted or initially stronger effects had significantly smaller sample sizes and tended to be older than those with replicated or unchallenged findings. There were no significant differences on the type of disease. The proportion of contradicted or initially stronger effects did not differ significantly across journals (_p_ = 0.60)...Small studies using surrogate markers may also sometimes lead to erroneous clinical inferences.^158^ There were only 2 studies with typical surrogate markers among the highly cited studies examined herein, but both were subsequently contradicted in their clinical extrapolations about the efficacy of nitric oxide 22 and hormone therapy.^42^
>
> Box 2. "Contradicted and Initially Stronger Effects in Control Studies Contradicted Findings":
>
> - In a prospective cohort,^91^ vitamin A was inversely related to breast cancer (relative risk in the highest quintile, 0.84; 95% confidence interval [CI], 0.71-0.98) and vitamin A supplementation was associated with a reduced risk (_p_ = 0.03) in women at the lowest quintile group; in a randomized trial^128^ exploring further the retinoid-breast cancer hypothesis, fenretinide treatment of women with breast cancer for 5 years had no effect on the incidence of second breast malignancies.
> - A trial (_n_ = 51) showed that cladribine significantly improved the clinical scores of patients with chronic progressive multiple sclerosis.^119^ In a larger trial of 159 patients, no significant treatment effects were found for cladribine in terms of changes in clinical scores.^129^
>
> *Initially Stronger Effects*:
>
> - A trial (_n_ = 28) of aerosolized ribavirin in infants receiving mechanical ventilation for severe respiratory syncytial virus infection^82^ showed significant decreases in mechanical ventilation (4.9 vs 9.9 days) and hospital stay (13.3 vs 15.0 days). A meta-analysis of 3 trials (_n_ = 104) showed a decrease of only 1.8 days in the duration of mechanical ventilation and a non-statistically-significant decrease of 1.9 days in duration of hospitalization.^130^
> - A trial (_n_ = 406) of intermittent diazepam administered during fever to prevent recurrence of febrile seizures^90^ showed a significant 44% relative risk reduction in seizures. The effect was smaller in other trials and the overall risk reduction was no longer formally significant^131^; moreover, the safety profile of diazepam was deemed unfavorable to recommend routine preventive use.
> - A case-control and cohort study evaluation^92^ showed that the increased risk of sudden infant death syndrome among infants who sleep prone is increased by use of natural-fiber mattresses, swaddling, and heating in bedrooms. Several observational studies have been done since, and they have provided inconsistent results on these interventions, in particular, they disagree on the possible role of overheating.^132^
> - A trial of 54 children^95^ showed that the steroid budenoside significantly reduced the croup score by 2 points at 4 hours, and significantly decreased readmissions by 86%. A meta-analysis (_n_ = 3736) 133 showed a significant improvement in the Westley score at 6 hours (1.2 points), and 12 hours (1.9 points), but not at 24 hours. Fewer return visits and/or (re)admissions occurred in patients treated with glucocorticoids, but the relative risk reduction was only 50% (95% CI, 24%-64%).
> - A trial (_n_ = 55) showed that misprostol was as effective as dinoprostone for termination of second-trimester pregnancy and was associated with fewer adverse effects than dinoprostone.^96^ A subsequent trial^134^ showed equal efficacy, but a higher rate of adverse effects with misoprostol (74%) than with dinoprostone (47%).
> - A trial (_n_ = 50) comparing botulinum toxin vs glyceryl trinitrate for chronic anal fissure concluded that both are effective alternatives to surgery but botulinum toxin is the more effective nonsurgical treatment (1 failure vs 9 failures with nitroglycerin).^109^ In a meta-analysis^135^ of 31 trials, botulinum toxin compared with placebo showed no significant efficacy (relative risk of failure, 0.75; 95% CI, 0.32-1.77), and was also no better than glyceryl trinitrate (relative risk of failure, 0.48; 95% CI, 0.211.10); surgery was more effective than medical therapy in curing fissure (relative risk of failure, 0.12; 95% CI, 0.07-0.22).
> - A trial of acetylcysteine (_n_ = 83) showed that it was highly effective in preventing contrast nephropathy (90% relative risk reduction).^110^ There have been many more trials and many meta-analyses on this topic. The latest meta-analysis^136^ shows a non-statistically-significant 27% relative risk reduction with acetylcysteine.
> - A trial of 129 stunted Jamaican children found that both nutritional supplementation and psychosocial stimulation improved the mental development of stunted children; children who got both interventions had additive benefits and achieved scores close to those of nonstunted children.^117^ With long-term follow-up, however, it was found that the benefits were small and the 2 interventions no longer had additive effects.^137^
>
> ...It is possible that high-profile journals may tend to publish occasionally very striking findings and that this may lead to some difficulty in replicating some of these findings.^163^ Poynard et al [["Truth Survival in Clinical Research: An Evidence-Based Requiem?"](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.456.8696&rep=rep1&type=pdf)] evaluated the conclusions of hepatology-related articles published between 1945 and 1999 and found that, overall, 60% of these conclusions were considered to be true in 2000 and that there was no difference between randomized and nonrandomized studies or high- vs low-quality studies. Allowing for somewhat different definitions, the higher rates of refutation and the generally worse performance of nonrandomized studies in the present analysis may stem from the fact that I focused on a selected sample of the most noticed and influential clinical research. For such highly cited studies, the turnaround of "truth" may be faster; in particular non-randomized studies may be more likely to be probed and challenged than non-randomized studies published in the general literature.
["Comparison of evidence on harms of medical interventions in randomized and nonrandomized studies"](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1389826/), Papanikolaou et al 2006:
> Background: Information on major harms of medical interventions comes primarily from epidemiologic studies performed after licensing and marketing. Comparison with data from large-scale randomized trials is occasionally feasible. We compared evidence from randomized trials with that from epidemiologic studies to determine whether they give different estimates of risk for important harms of medical interventions.
>
> Method: We targeted well-defined, specific harms of various medical interventions for which data were already available from large-scale randomized trials (> 4000 subjects). Nonrandomized studies involving at least 4000 subjects addressing these same harms were retrieved through a search of MEDLINE. We compared the relative risks and absolute risk differences for specific harms in the randomized and nonrandomized studies.
>
> Results: Eligible nonrandomized studies were found for 15 harms for which data were available from randomized trials addressing the same harms. Comparisons of relative risks between the study types were feasible for 13 of the 15 topics, and of absolute risk differences for 8 topics. The estimated increase in relative risk differed more than 2-fold between the randomized and nonrandomized studies for 7 (54%) of the 13 topics; the estimated increase in absolute risk differed more than 2-fold for 5 (62%) of the 8 topics. There was no clear predilection for randomized or nonrandomized studies to estimate greater relative risks, but usually (75% [6/8]) the randomized trials estimated larger absolute excess risks of harm than the nonrandomized studies did.
>
> Interpretation: Nonrandomized studies are often conservative in estimating absolute risks of harms. It would be useful to compare and scrutinize the evidence on harms obtained from both randomized and nonrandomized studies.
>
> ...In total, data from nonrandomized studies could be juxtaposed against data from randomized trials for 15 of the 66 harms (Table 1). All of the studied harms were serious and clinically relevant. The interventions included drugs, vitamins, vaccines and surgical procedures. A large variety of prospective and retrospective approaches were used in the nonrandomized studies, including both controlled and uncontrolled designs (Table 1)...For 5 (38%) of the 13 topics for which estimated increases in relative risk could be compared, the increase was greater in the nonrandomized studies than in the respective randomized trials; for the other 8 topics (62%), the increase was greater in the randomized trials. The estimated increase in relative risk differed more than 2-fold between the randomized and nonrandomized studies for 7 (54%) of the 13 topics (symptomatic intracranial bleed with oral anticoagulant therapy [topic 5], major extracranial bleed with anticoagulant v. antiplatelet therapy [topic 6], symptomatic intracranial bleed with ASA [topic 8], vascular or visceral injury with laparoscopic v. open surgical repair of inguinal hernia [topic 10], major bleed with platelet glycoprotein IIb/IIIa blocker therapy for percutaneous coronary intervention [topic 14], multiple gestation with folate supplementation [topic 13], and acute myocardial infarction with rofecoxib v. naproxen therapy [topic 15]). Differences in relative risk beyond chance between the randomized and nonrandomized studies occurred for 2 of the 13 topics: the relative risks for symptomatic intracranial bleed with oral anticoagulant therapy (topic 5) and for vascular or visceral injury with laparoscopic versus open surgical repair of inguinal hernia (topic 10) were significantly greater in the nonrandomized studies than in the randomized trials. Between-study heterogeneity was more common in the syntheses of data from the nonrandomized studies than in the syntheses of data from the randomized trials. There was significant between-study heterogeneity (p < 0.10 on the Q statistic) among the randomized trials for 2 data syntheses (topics 3 and 14) and among the nonrandomized studies for 5 data syntheses (topics 4, 7, 8, 13 and 15). The adjusted and unadjusted estimates of relative risk in the nonrandomized studies were similar (see online Appendix 4, available at www.cmaj.ca/cgi/content/full/cmaj.050873/DC1)...The randomized trials usually estimated larger absolute risks of harms than the nonrandomized studies did; for 1 topic, the difference was almost 40-fold.
Young & Karr 2011, ["Deming, data and observational studies: A process out of control and needing fixing"](/doc/statistics/causality/2011-young.pdf):
> As long ago as 1988^1,2^ it was noted that there were contradicted results for case-control studies in 56 different topic areas, of which cancer and things that cause it or cure it were by far the most frequent. An average of 2.4 studies supported each association - and an average of 2.3 studies did not support it. For example, 3 studies supported an association between the anti-depressant drug reserpine and breast cancer, and 8 did not. It was asserted^2^ that "much of the disagreement may occur because a set of rigorous scientific principles has not yet been accepted to guide the design or interpretation of case-control research".
>
> 1. Mayes et al 1988, ["A collection of 56 topics with contradictory results in case-control research"](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.830.8346&rep=rep1&type=pdf)
#. Feinstein 1988, ["Scientific standards in epidemiologic studies of the menace of daily life"](/doc/statistics/causality/1988-feinstein.pdf)
>
> ...We ourselves carried out an informal but comprehensive accounting of 12 randomized clinical trials that tested observational claims - see Table 1. The 12 clinical trials tested 52 observational claims. They all confirmed no claims in the direction of the observational claims. We repeat that figure: 0 out of 52. To put it another way, 100% of the observational claims failed to replicate. In fact, 5 claims (9.6%) are statistically-significant in the clinical trials in the opposite direction to the observational claim. To us, a false discovery rate of over 80% is potent evidence that the observational study process is not in control. The problem, which has been recognised at least since 1988, is systemic.
>
> ...The "females eating cereal leads to more boy babies" claim translated the cartoon example into real life. The claim appeared in the _Proceedings of the Royal Society, Series B_. It makes essentially no biological sense, as for humans the Y chromosome controls gender and comes from the male parent. The data set consisted of the gender of children of 740 mothers along with the results of a food questionnaire, not of breakfast cereal alone but of 133 different food items - compared to only 20 colours of jelly beans. Breakfast cereal during the second time period at issue was one of the few foods of the 133 to give a positive. We reanalysed the data^6^, with 262 _t_-tests, and concluded that the result was easily explained as pure chance.
>
> 6. Young et al 2009, ["Cereal-induced gender selection? Most likely a multiple testing false positive"](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2660953/)
>
> ...The US Center for Disease Control assayed the urine of around 1000 people for 275 chemicals, one of which was bisphenol A (BPA). One resulting claim was that BPA is associated with cardiovascular diagnoses, diabetes, and abnormal liver enzyme concentrations. BPA is a chemical much in the news and under attack from people fearful of chemicals. The people who had their urine assayed for chemicals also gave a self-reported health status for 32 medical outcomes. For each person, ten demographic variables (such as ethnicity, education, and income) were also collected. There are 275 × 32 = 8800 potential endpoints for analysis. Using simple linear regression for covariate adjustment, there are approximately 1000 potential models, including or not including each demographic variable. Altogether the search space is about 9 million models and endpoints^11^. The authors remain convinced that their claim is valid.
>
> 11. Young, S. S. and Yu, M. (2009) ["To the Editor: Association of Bisphenol A With Diabetes and Other Abnormalities"](/doc/statistics/causality/2009-young.pdf). _Journal of the American Medical Association_, 301, 720-721
["Vitamin D and multiple health outcomes: umbrella review of systematic reviews and meta-analyses of observational studies and randomized trials"](https://www.bmj.com/content/348/bmj.g2035.full), Theodoratou et al 2014:
> Comparison of findings from observational studies and clinical trials:
>
> One hundred and twenty three (90%) outcomes were examined only by syntheses of observational evidence (_n_ = 84) or only by meta-analyses of randomized evidence (_n_ = 39), so we could not compare observational and randomized evidence.
>
> Ten (7%) outcomes were examined by both meta-analyses of observational studies and meta-analyses of randomized controlled trials: cardiovascular disease, hypertension, birth weight, birth length, head circumference at birth, small for gestational age birth, mortality in patients with chronic kidney disease, all cause mortality, fractures, and hip fractures (table 5⇓). The direction of the association/effect and level of statistical-significance was concordant only for birth weight, but this outcome could not be tested for hints of bias in the meta-analysis of observational studies (owing to lack of the individual data). The direction of the association/effect but not the level of statistical-significance was concordant in six outcomes (cardiovascular disease, hypertension, birth length, head circumference small for gestational age births, and all cause mortality), but only two of them (cardiovascular disease and hypertension) could be tested and were found to be free from hint of bias and of low heterogeneity in the meta-analyses of observational studies. For mortality in chronic kidney disease patients, fractures in older populations, and hip fractures, both the direction and the level of significance of the association/effect were not concordant.
["Agreement of treatment effects for mortality from routinely collected data and subsequent randomized trials: meta-epidemiological survey"](https://www.bmj.com/content/352/bmj.i493), Hemkens et al 2016:
> *Objective*: To assess differences in estimated treatment effects for mortality between observational studies with routinely collected health data (RCD; that are published before trials are available) and subsequent evidence from randomized controlled trials on the same clinical question.
>
> *Design*: Meta-epidemiological survey.
>
> *Data sources*: PubMed searched up to November 2014.
>
> *Methods*: Eligible RCD studies were published up to 2010 that used propensity scores to address confounding bias and reported comparative effects of interventions for mortality. The analysis included only RCD studies conducted before any trial was published on the same topic. The direction of treatment effects, confidence intervals, and effect sizes (odds ratios) were compared between RCD studies and randomized controlled trials. The relative odds ratio (that is, the summary odds ratio of trial(s) divided by the RCD study estimate) and the summary relative odds ratio were calculated across all pairs of RCD studies and trials. A summary relative odds ratio greater than one indicates that RCD studies gave more favorable mortality results.
>
> *Results*: The evaluation included 16 eligible RCD studies, and 36 subsequent published randomized controlled trials investigating the same clinical questions (with 17,275 patients and 835 deaths). Trials were published a median of three years after the corresponding RCD study. For five (31%) of the 16 clinical questions, the direction of treatment effects differed between RCD studies and trials. Confidence intervals in nine (56%) RCD studies did not include the RCT effect estimate. Overall, RCD studies showed significantly more favorable mortality estimates by 31% than subsequent trials (summary relative odds ratio 1.31 (95% confidence interval 1.03 to 1.65; I^2^=0%)).
>
> *Conclusions*: Studies of routinely collected health data could give different answers from subsequent randomized controlled trials on the same clinical questions, and may substantially overestimate treatment effects. Caution is needed to prevent misguided clinical decision making.
["Residual Confounding in Health Plan Performance Assessments: Evidence From Randomization in Medicaid"](/doc/statistics/causality/2022-wallace.pdf), Wallace et al 2022:
>**Objective**:
> To assess the degree to which risk-adjusted measures of health plan performance adequately adjust for the variation across plans that arises because of differences in patient characteristics (residual confounding).
>
> **Design**:
> Comparison between plan performance estimates based on enrollees who made plan choices (observational population) and estimates based on enrollees assigned to plans (randomized population).
>
> **Setting**:
> [natural experiment](https://en.wikipedia.org/wiki/Natural_experiment) in which more than 2⁄3^rd^s of a state’s Medicaid population in 1 region was randomly assigned to 1 of 5 plans.
>
> **Participants**:
> 137 933 enrollees in 2013 to 2014 in Louisiana, of whom 31.1% selected a plan and 68.9% were randomly assigned to 1 of the same 5 plans.
>
> **Measurements**:
> Annual total spending (that is, payments to providers), primary care use, dental care use, and avoidable [emergency department](https://en.wikipedia.org/wiki/Emergency_department) visits, all scored as plan-specific deviations from the “average” plan performance within each population.
>
> **Results**:
> Enrollee characteristics were appreciably imbalanced across plans in the observational population, as expected, but were not in the randomized population. Annual total spending varied across plans more in the observational population (SD, [$147]($2013) per enrollee) than in the randomized population (SD, [$70]($2013) per enrollee) after accounting for baseline differences in the observational and randomized populations and for differences across plans.
>
> On average, a plan’s spending score (its deviation from the “average” performance) in the observational population differed from its score in the randomized population by [$67]($2013) per enrollee in absolute value (95% CI, [$38]($2013) to [$123]($2013)), or 4.2% of mean spending per enrollee (_p_ = 0.009, rejecting the [null hypothesis](https://en.wikipedia.org/wiki/Null_hypothesis) that this difference would be expected from [sampling error](https://en.wikipedia.org/wiki/Sampling_error)).
>
> The difference was reduced modestly by risk adjustment to [$62]($2013) per enrollee (_p_ = 0.012). [Residual confounding](/note/regression "‘Regression To The Mean Fallacies’, Branwen 2021") was similarly substantial for most other performance measures. Further adjustment for social factors did not materially change estimates...Despite a high patient-level R^2^ of 29% for health care spending, indicating that the enrollee variables included in our risk-adjustment approach captured more than a quarter of the variation in the outcome, risk adjustment did not meaningfully reduce confounding at the plan level for spending in our study.
>
> ![**Figure 1**: _Differences in plan total health care spending scores derived from the observational and randomized populations._ Each bar corresponds to 1 of the 5 plans. The [blue area]{.smallcaps} of the bar corresponds to a plan’s randomized spending score (relative to the “average” plan mean) based on the randomly assigned population. The [orange]{.smallcaps} bar corresponds to a plan’s spending score based on the observational population before risk adjustment. The [grey]{.smallcaps} unhatched portion indicates the difference between the 2 scores, or the extent of residual confounding in the observational scores. For these 5 Medicaid plans, higher-cost enrollees selected plans that control spending to a lesser extent. We calculated a plan score for each plan equal to the plan’s deviation from the population-specific plan mean. We compared plan scores between the 2 populations, instead of raw plan means, because population means differed somewhat. Thus, we compared how a plan performed relative to other plans in 1 population with its relative performance in the other population.](/doc/statistics/causality/2022-wallace-figure1-differencebetweenrandomizedandcorelationalestimatesfromlouisianamedicaidnaturalexperiment.jpg)
# Economics
["Evaluating the Econometric Evaluations of Training Programs with Experimental Data"](/doc/economics/1986-lalonde.pdf), LaLonde 1986:
> This paper compares the effect on trainee earnings of an employment program that was run as a field experiment where participants were randomly assigned to treatment and control groups with the estimates that would have been produced by an econometrician. This comparison shows that many of the econometric procedures do not replicate the experimentally determined results, and it suggests that researchers should be aware of the potential for specification errors in other nonexperimental evaluations.
>
> ...The National Supported Work Demonstration (NSW) was a temporary employment program designed to help disadvantaged workers lacking basic job skills move into the labor market by giving them work experience and counseling in a sheltered environment. Unlike other federally sponsored employment and training programs, the NSW program assigned qualified applicants to training positions randomly. Those assigned to the treatment group received all the benefits of the NSW program, while those assigned to the control group were left to fend for themselves.^3^
> During the mid-1970s, the Manpower Demonstration Research Corporation (MDRC) operated the NSW program in ten sites across the United States. The MDRC admitted into the program AFDC women, ex-drug addicts, ex-criminal offenders, and high school dropouts of both sexes.^4^ For those assigned to the treatment group, the program guaranteed a job for 9 to 18 months, depending on the target group and site. The treatment group was divided into crews of three to five participants who worked together and met frequently with an NSW counselor to discuss grievances and performance. The NSW program paid the treatment group members for their work. The wage schedule offered the trainees lower wage rates than they would have received on a regular job, but allowed their earnings to increase for satisfactory performance and attendance. The trainees could stay on their supported work jobs until their terms in the program expired and they were forced to find regular employment.
> ...male and female participants frequently performed different sorts of work. The female participants usually worked in service occupations, whereas the male participants tended to work in construction occupations. Consequently, the program costs varied across the sites and target groups. The program cost \$9,100 per AFDC participant and approximately \$6,800 for the other target groups' trainees.
>
> The first two columns of Tables 2 and 3 present the annual earnings of the treatment and control group members.^9^ The earnings of the experimental groups were the same in the pre-training year 1975, diverged during the employment program, and converged to some extent after the program ended. The post-training year was 1979 for the AFDC females and 1978 for the males.^10^ Columns 2 and 3 in the first row of Tables 4 and 5 show that both the unadjusted and regression-adjusted pre-training earnings of the two sets of treatment and control group members are essentially identical. Therefore, because of the NSW program's experimental design, the difference between the post-training earnings of the experimental groups is an unbiased estimator of the training effect, and the other estimators described in columns 5-10(11) are unbiased estimators as well. The estimates in column 4 indicate that the earnings of the AFDC females were \$851 higher than they would have been without the NSW program, while the earnings of the male participants were \$886 higher.^11^ Moreover, the other columns show that the econometric procedure does not affect these estimates.
>
> The researchers who evaluated these federally sponsored programs devised both experimental and nonexperimental procedures to estimate the training effect, because they recognized that the difference between the trainees' pre- and post-training earnings was a poor estimate of the training effect. In a dynamic economy, the trainees' earnings may grow even without an effective program. The goal of these program evaluations is to estimate the earnings of the trainees had they not participated in the program. Researchers using experimental data take the earnings of the control group members to be an estimate of the trainees' earnings without the program. Without experimental data, researchers estimate the earnings of the trainees by using the regression-adjusted earnings of a comparison group drawn from the population. This adjustment takes into account that the observable characteristics of the trainees and the comparison group members differ, and their unobservable characteristics may differ as well.
>
> The first step in a nonexperimental evaluation is to select a comparison group whose earnings can be compared to the earnings of the trainees. Tables 2 and 3 present the mean annual earnings of female and male comparison groups drawn from the Panel Study of Income Dynamics (PSID) and Westat's Matched Current Population Survey - Social Security Administration File (CPS-SSA). These groups are characteristic of two types of comparison groups frequently used in the program evaluation literature. The PSID-1 and the CPS-SSA-1 groups are large, stratified random samples from populations of household heads and households, respectively.^14^ The other, smaller, comparison groups are composed of individuals whose characteristics are consistent with some of the eligibility criteria used to admit applicants into the NSW program. For example, the PSID-3 and CPS-SSA-4 comparison groups in Table 2 include females from the PSID and the CPS-SSA who received AFDC payments in 1975, and were not employed in the spring of 1976. Tables 2 and 3 show that the NSW trainees and controls have earnings histories that are more similar to those of the smaller comparison groups
>
> Unlike the experimental estimates, the nonexperimental estimates are sensitive both to the composition of the comparison group and to the econometric procedure. For example, many of the estimates in column 9 of Table 4 replicate the experimental results, while other estimates are more than \$1,000 larger than the experimental results. More specifically, the results for the female participants (Table 4) tend to be positive and larger than the experimental estimate, while for the male participants (Table 5), the estimates tend to be negative and smaller than the experimental impact.^20^ Additionally, the nonexperimental procedures replicate the experimental results more closely when the nonexperimental data include pretraining earnings rather than cross-sectional data alone or when evaluating female rather than male participants.
>
> Before taking some of these estimates too seriously, many econometricians at a minimum would require that their estimators be based on econometric models that are consistent with the pre-training earnings data. Thus, if the regression-adjusted difference between the post-training earnings of the two groups is going to be a consistent estimator of the training effect, the regression-adjusted pretraining earnings of the two groups should be the same.
> Based on this specification test, econometricians might reject the nonexperimental estimates in columns 4-7 of Table 4 in favor of the ones in columns 8-11. Few econometricians would report the training effect of \$870 in column 5, even though this estimate differs from the experimental result by only \$19. If the cross-sectional estimator properly controlled for differences between the trainees and comparison group members, we would not expect the difference between the regression adjusted pre-training earnings of the two groups to be \$1,550, as reported in column 3. Likewise, econometricians might refrain from reporting the difference in differences estimates in columns 6 and 7, even though all these estimates are within two standard errors of \$3,000. As noted earlier, this estimator is not consistent with the decline in the trainees' pre-training earnings.
>
> The two-step estimates are usually closer than the one-step estimates to the experimental results for the male trainees as well. One estimate, which used the CPS-SSA-1 sample as a comparison group, is within \$600 of the experimental result, while the one-step estimate falls short by \$1,695. The estimates of the participation coefficients are negative, although unlike these estimates for the females, they are always significantly different from zero. This finding is consistent with the example cited earlier in which individuals with high participation unobservables and low earnings unobservables were more likely to be in training. As predicted, the unrestricted estimates are larger than the one-step estimates. However, as with the results for the females, this procedure may leave econometricians with a considerable range (\$1,546) of imprecise estimates
["The Endogeneity Problem in Developmental Studies"](/doc/statistics/causality/2004-duncan.pdf), Duncan et al 2004:
> For example, despite theoretical arguments to the contrary, most empirical studies of the effects of divorce on children have assumed that divorce is randomly assigned to children. They do this by failing to control for the fact that divorce is the product of the parents' temperaments, resources, and other stressors that face parents, most of which will influence children's outcomes in their own right. As a result, studies comparing developmental outcomes of children with and without past parental divorces after controlling for a handful of family background characteristics are likely to confound the effects of divorce with the effects of unmeasured parent and child variables. Indeed, studies that control for children's behavior problems prior to a possible divorce find much smaller apparent effects of the divorce itself (Cherlin, Chase-Lansdale, & McRae, 1998).
>
> - Cherlin, A., Chase-Lansdale, L. P., & McRae, C. (1998). ["Effects of parental divorce on mental health throughout the life course"](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.625.1731&rep=rep1&type=pdf). _American Sociological Review_, 63, 239-249
>
> ... These experiments can provide researchers with some sense for the bias that results from nonexperimental estimates as well as providing direct evidence for the causal effects of some developmental influence of interest. For example, Wilde & Hollister 2002 compare nonexperimental and experimental results for the widely cited Tennessee Student-Teacher Achievement Ratio (STAR) class-size experiment. The STAR experiment provides an unbiased estimate of the impact of class size on student achievement by comparing the average achievement levels of students assigned to small (experimental) and regular (control) classrooms. However, Wilde and Hollister also estimated a series of more conventional nonexperimental regressions that related naturally occurring class size variation within the set of regular classrooms to student achievement, controlling for an extensive set of student demographic characteristics and socioeconomic status.
>
> - Wilde & Hollister 2002, ["How close is close enough? Testing nonexperimental estimates of impact against experimental estimates of impact with education test scores as outcomes"](#wilde-hollister-2002)
>
> Table 1 compares the experimental and nonexperimental estimates of class size impacts by school. The table shows substantial variability across schools in the effects of smaller classes on student standardized test scores. In some cases (eg. Schools B, D, and I), the two sets of estimates are quite close, but in some (eg. Schools C, E, G, and H) they are quite different. A comparison of the nonexperimental and experimental results as a whole reveals that the average bias (ie. the absolute difference between the experimental and nonexperimental impact estimates) is on the order of 10 percentile points - about the same as the average experimental estimate for the effects of smaller classes!
>
>
>
> School Nonexperimental Regression Experimental Estimate
> ------- -------------------------- ---------------------
> A 9.6 -5.2
> B 15.3✱ 13.0✱
> C 1.9 24.1✱
> D 35.2✱ 33.1✱
> E 20.4✱ -10.5
> F 0.2 1.3
> G -8.6 10.6✱
> H -5.6 9.6✱
> I 16.5✱ 14.7✱
> J 24.3✱ 16.2✱
> K 27.8* 19.3✱
>
> Table: **Table 1**: Comparison of Experimental and Nonexperimental Estimates for Effects of Class Size on Student Test Scores [✱ = estimate statistically-significant at the 5% cutoff.]
>
> A second example of the bias that may result with nonexperimental estimates comes from the U.S. Department of Housing and Urban Development's Moving to Opportunity (MTO) housing-voucher experiment, which randomly assigned housing-project residents in high-poverty neighborhoods of five of the nation's largest cities to either a group that was offered a housing voucher to relocate to a lower poverty area or to a control group that received no mobility assistance under the program (Ludwig, Duncan, & Hirschfield, 2001). Because of well-implemented random assignment, each of the groups on average should be equivalent (subject to sampling variability) with respect to all observable and unobservable preprogram characteristics.
>
> - Ludwig, J. (1999). "Experimental and non-experimental estimates of neighborhood effects on low-income families". Unpublished document, Georgetown University.
> - Ludwig, J., Duncan, G., & Hirschfield, P. (2001). ["Urban poverty and juvenile crime: Evidence from a randomized housing-mobility experiment"](https://www.nber.org/programs-projects/projects-and-centers/moving-opportunity). _Quarterly Journal of Economics_, 116, 655-680.
>
> Table 2 presents the results of using the randomized design of MTO to generate unbiased estimates of the effects of moving from high- to low-poverty census tracts on teen crime. The experimental estimates are the difference between average outcomes of all families offered vouchers and those assigned to the control group, divided by the difference across the two groups in the proportion of families who moved to a low-poverty area. (Note the implication that these kinds of experimental data can be used to produce unbiased estimates of the effects of neighborhood characteristics on developmental outcomes, even if the takeup rate is less than 100% in the treatment group and greater than 0% among the control group.)^4^ The nonexperimental estimates simply compare families who moved to low-poverty neighborhoods with those who did not, ignoring information about each family's random assignment and relying on the set of prerandom assignment measures of MTO family characteristics to adjust for differences between families who chose to move and those who do not.^5^ As seen in Table 2, even after statistically adjusting for a rich set of background characteristics the nonexperimental measure-the-unmeasured approach leads to starkly different inferences about the effects of residential mobility compared with the unbiased experimental estimates. For example, the experimental estimates suggest that moving from a high- to a low- poverty census tract significantly reduces the number of violent crimes. In contrast, the nonexperimental estimates find that such moves have essentially no effect on violent arrests. In the case of "other" crimes, the nonexperimental estimates suggest that such moves reduce crime, but the experimentally based estimates do not.
>
>
>
> Measure Experimental SE Non-experimental SE Sample Size
> ------------------ -------------- ----- ------------------ ----- --------------
> Violent Crime -47.4\* 24.3 -4.9 12.5 259
> Property Crime 29.7 28.9 -10.8 14.1 259
> Other Crimes -0.6 37.4 -36.9\* 14.3 259
>
> Table: Table 2, Estimated Impacts of Moving From a High- to a Low-Poverty Neighborhood on Arrests Per 100 Juveniles [From Ludwig (1999), based on data from the Baltimore Moving to Opportunity experiment. Regression models also control for baseline measurement of gender, age at random assignment, and preprogram criminal involvement, family's preprogram victimization, mother's schooling, welfare receipt and marital status. \* = estimated effect of dropout program on dropout rates statistically-significant at the 5% cutoff level.]
>
>
>
> ...A final example comes from the National Evaluation of Welfare-to-Work Strategies, randomized experiment designed to evaluate welfare-to-work programs in seven sites across the United States. One of the treatment streams encouraged welfare-recipient mothers to participate in education activities. In addition to measuring outcomes such as clients' welfare receipt, employment, and earnings, the evaluation study also tested young children's school readiness using the Bracken Basic Concepts Scale School Readiness Subscale. Using a method for generating experimental estimates similar to that used in the MTO analyses, Magnuson and McGroder (2002) examined the effects of the experimentally induced increases in maternal schooling on children's school readiness. Again, the results suggest that nonexperimental estimates did not closely reproduce experimentally based estimates.
>
> - Magnuson, K. A., & McGroder, S. (2002). ["The effect of increasing welfare mothers' education on their young children's academic problems and school readiness"](/doc/sociology/2003-magnuson.pdf "‘The Effect of Increases in Welfare Mothers' Education on Their Young Children's Academic and Behavioral Outcomes: Evidence from the National Evaluation of Welfare-to-Work Strategies Child Outcomes Study’, Magnuson 2003"). Joint Center for Poverty Research, Working Paper No. 280, Northwestern University.
>
> A much larger literature within economics, statistics, and program evaluation has focused on the ability of nonexperimental regression-adjustment methods to replicate experimental estimates for the effects of job training or welfare-to-work programs. Although the "contexts" represented by these programs may be less interesting to developmentalists, the results of this literature nevertheless bear directly on the question considered in this article: Can regression methods with often quite detailed background covariates reproduce experimental impact estimates for such programs? As one recent review concluded, "Occasionally, but not in a way that can be easily predicted" (Glazerman, Levy, & Myers, 2002, p. 46; see also Bloom, Michalopoulos, Hill, & Lei, 2002).
>
> - Glazerman, S., Levy, D., & Myers, D. (2002). [_Nonexperimental replications of social experiments: A systematic review_](https://www.mathematica.org/-/media/publications/pdfs/nonexperimentalreps.pdf). Washington, DC: Mathematica Policy Research
> - Bloom, H. S., Michalopoulos, C., Hill, C., & Lei, Y. (2002) [_Can non-experimental comparison group methods match the findings from a random assignment evaluation of mandatory welfare-to-work programs?_](https://files.eric.ed.gov/fulltext/ED471814.pdf "'Can Nonexperimental Comparison Group Methods Match the Findings from a Random Assignment Evaluation of Mandatory Welfare-to-Work Programs? MDRC Working Papers on Research Methodology', Bloom et al 2002") New York: Manpower Demonstration Research Corporation.
Allcott 2011, ["Social Norms and Energy Conservation"](https://www.lexissecuritiesmosaic.com/gateway/FedReg/1_allcott_2011_jpubec_-_social_norms_and_energy_conservation.pdf):
> Nearly all energy efficiency programs are still evaluated using non-experimental estimators or engineering accounting approaches. How important is the experimental control group to consistently-estimated ATEs? This issue is crucial for several of OPOWER's initial programs that were implemented without a control group but must estimate impacts to report to state regulators. While LaLonde (1986) documented that non-experimental estimators performed poorly in evaluating job training programs and similar arguments have been made in many other domains, weather-adjusted non-experimental estimators could in theory perform well in modeling energy demand. The importance of randomized controlled trials has not yet been clearly documented to analysts and policymakers in this context.
>
> Without an experimental control group, there are two econometric approaches that could be used. The first is to use a difference estimator, comparing electricity use in the treated population before and after treatment. In implementing this, I control for weather differences non-parametrically, using bins with width one average degree day. This slightly outperforms the use of fourth degree polynomials in heating and cooling degree-days. This estimator is unbiased if and only if there are no other factors associated with energy demand that vary between the pre-treatment and post-treatment period. A second non-experimental approach is to use a difference-in-differences estimator with nearby households as a control group. For each experiment, I form a control group using the average monthly energy use of households in other utilities in the same state, using data that regulated utilities report to the U.S. Department of Energy on Form EIA 826. The estimator includes utility-by-month fixed effects to capture different seasonal patterns - for example, there may be local variation in how many households use electric heat instead of natural gas or oil, which then affects winter electricity demand. This estimator is unbiased if and only if there are no unobserved factors that differentially affect average household energy demand in the OPOWER partner utility vs. the other utilities in the same state. Fig. 6 presents the experimental ATEs for each experiment along with point estimates for the two types of non-experimental estimators. There is substantial variance in the non-experimental estimators: the average absolute errors for the difference and difference-in-differences estimators, respectively, are 2.1% and 3.0%. Across the 14 experiments, the estimators are also biased on average. In particular, the mean of the ATEs from the difference-in-differences estimator is −3.75%, which is nearly double the mean of the experimental ATEs.
>
> ...What's particularly insidious about the non-experimental estimates is that they would appear quite plausible if not compared to the experimental benchmark. Nearly all are within the confidence intervals of the small sample pilots by Schultz et al 2007 and Nolan et al 2008 that were discussed above. Evaluations of similar types of energy use information feedback programs have reported impacts of zero to 10% (Darby, 2006).
["What Do Workplace Wellness Programs Do? Evidence from the Illinois Workplace Wellness Study"](/doc/statistics/causality/2018-jones.pdf), Jones et al 2018:
> Workplace wellness programs cover over 50 million workers and are intended to reduce medical spending, increase productivity, and improve well-being. Yet, limited evidence exists to support these claims. We designed and implemented a comprehensive workplace wellness program for a large employer with over 12,000 employees, and randomly assigned program eligibility and financial incentives at the individual level. Over 56% of eligible (treatment group) employees participated in the program. We find strong patterns of selection: during the year prior to the intervention, program participants had lower medical expenditures and healthier behaviors than non-participants. However, we do not find significant causal effects of treatment on total medical expenditures, health behaviors, employee productivity, or self-reported health status in the first year. Our 95% confidence intervals rule out 83% of previous estimates on medical spending and absenteeism. Our selection results suggest these programs may act as a screening mechanism: even in the absence of any direct savings, differential recruitment or retention of lower-cost participants could result in net savings for employers.
>
> ...We invited 12,459 benefits-eligible university employees to participate in our study.^3^ Study participants (_n_ = 4, 834) assigned to the treatment group (_n_ = 3, 300) were invited to take paid time off to participate in our workplace wellness program. Those who successfully completed the entire program earned rewards ranging from \$50 to \$350, with the amounts randomly assigned and communicated at the start of the program. The remaining subjects (_n_ = 1,534) were assigned to a control group, which was not permitted to participate. Our analysis combines individual-level data from online surveys, university employment records, health insurance claims, campus gym visit records, and administrative records from a popular community running event. We can therefore examine outcomes commonly studied by the prior literature (namely, medical spending and employee absenteeism) as well as a large number of novel outcomes.
>
> ...Third, we do not find significant effects of our intervention on 37 out of the 39 outcomes we examine in the first year following random assignment. These 37 outcomes include all our measures of medical spending, productivity, health behaviors, and self-reported health. We investigate the effect on medical expenditures in detail, but fail to find significant effects on different quantiles of the spending distribution or on any major subcategory of medical expenditures (pharmaceutical drugs, office, or hospital). We also do not find any effect of our intervention on the number of visits to campus gym facilities or on the probability of participating in a popular annual community running event, two health behaviors that are relatively simple for a motivated employee to change over the course of one year. These null estimates are meaningfully precise, particularly for two key outcomes of interest in the literature: medical spending and absenteeism. Our 95% confidence intervals rule out 83% of the effects reported in 115 prior studies, and the 99% confidence intervals for the return on investment (ROI) of our intervention rule out the widely cited medical spending and absenteeism ROI's reported in the meta-analysis of Baicker, Cutler & Song 2010. In addition, we show that our OLS (non-RCT) estimate for medical spending is in line with estimates from prior observational studies, but is ruled out by the 95% confidence interval of our IV (RCT) estimate. This demonstrates the value of employing an RCT design in this literature.
>
> ...Our randomized controlled design allows us to establish reliable causal effects by comparing outcomes across the treatment and control groups. By contrast, most existing studies rely on observational comparisons between participants and non-participants (see Pelletier, 2011, and Chapman, 2012, for reviews). Reviews of the literature have called for additional research on this topic and have also noted the potential for publication bias to skew the set of existing results (Baicker, Cutler and Song, 2010; Abraham and White, 2017). To that end, our intervention, empirical specifications, and outcome variables were prespecified and publicly archived. In addition, the analyses in this paper were independently replicated by a J-PAL affiliated researcher.
>
> ...Figure 8 illustrates how our estimates compare to the prior literature. The top-left figure in Panel (a) plots the distribution of the intent-to-treat (ITT) point estimates for medical spending from 22 prior workplace wellness studies. The figure also plots our ITT point estimate for total medical spending from Table 4, and shows that our 95% confidence interval rules out 20 of these 22 estimates. For ease of comparison, all effects are expressed as % changes. The bottom-left figure in Panel (a) plots the distribution of treatment-on-the-treated (TOT) estimates for health spending from 33 prior studies, along with the IV estimates from our study. In this case, our 95% confidence interval rules out 23 of the 33 studies (70%). Overall, our confidence intervals rule out 43 of 55 (78%) prior ITT and TOT point estimates for health spending. The two figures in Panel (b) repeat this exercise for absenteeism, and show that our estimates rule out 53 of 60 (88%) prior ITT and TOT point estimates for absenteeism. Across both sets of outcomes, we rule out 96 of 115 (83%) prior estimates. We can also combine our spending and absenteeism estimates with our cost data to calculate a return on investment (ROI) for workplace wellness programs. The 99% confidence intervals for the ROI associated with our intervention rule out the widely cited savings estimates reported in the meta-analysis of Baicker, Cutler & Song 2010.
>
> ![**Figure 8**: _Comparison of experimental estimates to prior studies._ \[Jones et al 2018: comparison of previous literature's correlational point-estimates with the Jones et al 2018 randomized effect's CI, demonstrating that almost none fall within the Jones et al 2018 CI.\]](/doc/statistics/causality/2018-jones-figure8-randomizedvscorrelationliterature.png)
>
> 4.3.3 IV versus OLS
>
> Across a variety of outcomes, we find very little evidence that our intervention had any effect in its first year. As shown above, our results differ from many prior studies that find significant reductions in health expenditures and absenteeism. One possible reason for this discrepancy is the presence of advantageous selection bias in these other studies, which are generally not randomized controlled trials. A second possibility is that there is something unique about our setting. We investigate these competing explanations by performing a typical observational (OLS) analysis and comparing its results to those of our experimental estimates.
>
> Specifically, we estimate _Y~i~_ = α + γPi + ΓXi + ε~_i_~, (5) where _Y~i~_ is the outcome variable as in (4), _P~i~_ is an indicator for participating in the screening and HRA, and _X~i~_ is a vector of variables that control for potentially non-random selection into participation. We estimate two variants of equation (5). The first is an instrumental variables (IV) specification that includes observations for individuals in the treatment or control groups, and uses treatment assignment as an instrument for completing the screening and HRA. The second variant estimates equation (5) using OLS, restricted to individuals in the treatment group. For each of these two variants, we estimate three specifications similar to those used for the ITT analysis described above (no controls, strata fixed effects, and post-Lasso).
>
> This generates six estimates for each outcome variable. Table 5 reports the results for our primary outcomes of interest. The results for all pre-specified administrative and survey outcomes are reported in Appendix Tables A.3e-A.3f.
>
> 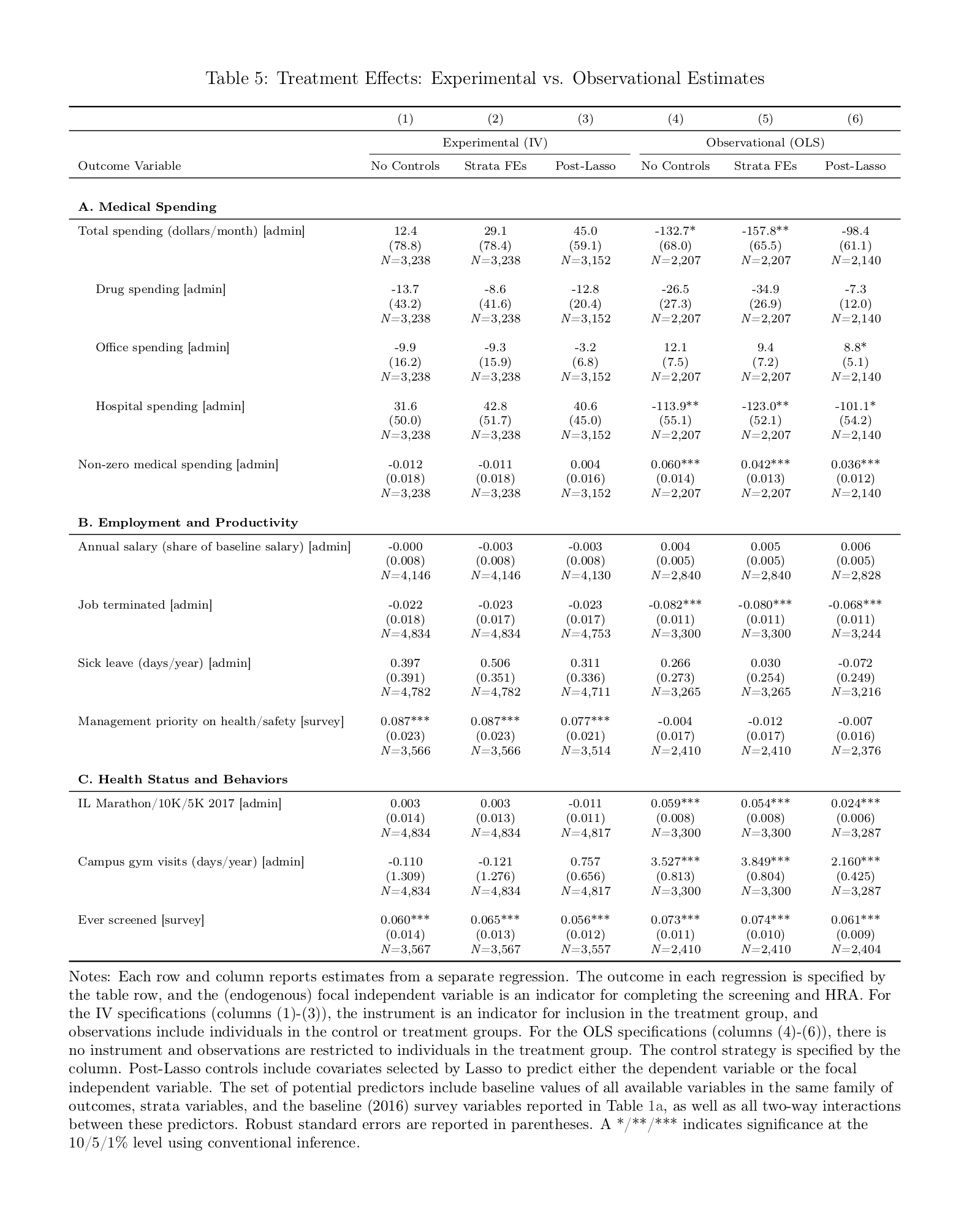{.width-full}
>
> .](/doc/psychology/cognitive-bias/2018-jones-table5-nyt-randomizedvscorrelation.png)
>
> As in our previous ITT analysis, the IV estimates reported in columns (1)-(3) are small and indistinguishable from zero for nearly every outcome. By contrast, the observational estimates reported in columns (4)-(6) are frequently large and statistically-significant. Moreover, the IV estimate rules out the OLS estimate for several key outcomes. Based on our most precise and well-controlled specification (post-Lasso), the OLS monthly spending estimate of -\$88.1 (row 1, column (6)) lies outside the 95% confidence interval of the IV estimate of \$38.5 with a standard error of \$58.8 (row 1, column (3)). For participation in the 2017 IL Marathon/10K/5K, the OLS estimate of 0.024 lies outside the 99% confidence interval of the corresponding IV estimate of -0.011 (standard error = 0.011). For campus gym visits, the OLS estimate of 2.160 lies just inside the 95% confidence interval of the corresponding IV estimate of 0.757 (standard error = 0.656). Under the assumption that the IV (RCT) estimates are unbiased, these difference imply that even after conditioning on a rich set of controls, participants selected into our workplace wellness program on the basis of lower-than-average contemporaneous spending and higher-than-average health activity. This is consistent with the evidence presented in §3.2 that pre-existing spending is lower, and pre-existing behaviors are healthier, among participants than among non-participants. In addition, the observational estimates presented in columns (4)-(6) are in line with estimates from previous observational studies, which suggests that our setting is not particularly unique. In the spirit of LaLonde (1986), these estimates demonstrate that even well-controlled observational analyses can suffer from significant selection bias in our setting, suggesting that similar biases might be at play in other wellness program settings as well.
>
> 
>
> 
>
> 
["Effect of a Workplace Wellness Program on Employee Health and Economic Outcomes: A Randomized Clinical Trial"](/doc/statistics/causality/2019-song.pdf), Song & Baicker 2019:
> *Design, Setting, & Participants*: This clustered randomized trial was implemented at 160 worksites from January 2015 through June 2016. Administrative claims and employment data were gathered continuously through June 30, 2016; data from surveys and biometrics were collected from July 1, 2016, through August 31, 2016.
>
> *Interventions*: There were 20 randomly selected treatment worksites (4037 employees) and 140 randomly selected control worksites (28 937 employees, including 20 primary control worksites [4106 employees]). Control worksites received no wellness programming. The program comprised 8 modules focused on nutrition, physical activity, stress reduction, and related topics implemented by registered dietitians at the treatment worksites.
>
> *Main Outcomes & Measures*: Four outcome domains were assessed. Self-reported health and behaviors via surveys (29 outcomes) and clinical measures of health via screenings (10 outcomes) were compared among 20 intervention and 20 primary control sites; health care spending and utilization (38 outcomes) and employment outcomes (3 outcomes) from administrative data were compared among 20 intervention and 140 control sites.
>
> *Results*: Among 32 974 employees (mean [SD] age, 38.6 [15.2] years; 15 272 [45.9%] women), the mean participation rate in surveys and screenings at intervention sites was 36.2% to 44.6% (_n_ = 4037 employees) and at primary control sites was 34.4% to 43.0% (_n_ = 4106 employees) (mean of 1.3 program modules completed). After 18 months, the rates for 2 self-reported outcomes were higher in the intervention group than in the control group: for engaging in regular exercise (69.8% vs 61.9%; adjusted difference, 8.3 percentage points [95% CI, 3.9-12.8]; adjusted _p_= 0.03) and for actively managing weight (69.2% vs 54.7%; adjusted difference, 13.6 percentage points [95% CI, 7.1-20.2]; adjusted _p_= 0.02). The program had no significant effects on other prespecified outcomes: 27 self-reported health outcomes and behaviors (including self-reported health, sleep quality, and food choices), 10 clinical markers of health (including cholesterol, blood pressure, and body mass index), 38 medical and pharmaceutical spending and utilization measures, and 3 employment outcomes (absenteeism, job tenure, and job performance).
>
> ...To assess endogenous selection into program participation, we compared the baseline characteristics of program participants to those of non-participants in treatment sites. To assess endogenous selection into participation in primary data collection, we compared baseline characteristics of workers who elected to provide clinical data or complete the health risk assessment to those of workers who did not, separately within the treatment group and the control group. This enabled us to assess any potential differential selection into primary data collection. Additionally, to examine differences in findings between our randomized trial approach and a standard observational design (and thereby any bias that confounding factors would have introduced into naive observational estimates), we generated estimates of program effects using ordinary least squares to compare program participants with nonparticipants (rather than using the variation generated by randomization).
>
> ...*Selection Into Program Participation*. Comparisons of preintervention characteristics between participants and nonparticipants in the treatment group provided evidence of potential selection effects. Participants were significantly more likely to be female, nonwhite, and full-time salaried workers in sales, although neither mean health care spending nor the probability of having any spending during the year before the program was significantly different between participants and nonparticipants (eTable 15 in Supplement 2)...an observational approach comparing workers who elected to participate with nonparticipants would have incorrectly suggested that the program had larger effects on some outcomes than the effects found using the controlled design, underscoring the importance of randomization to obtain unbiased estimates ([eTable 17 in Supplement 2](/doc/statistics/causality/2019-song-supplement2.pdf#page=45)).
# Sociology
["How Close Is Close Enough? Testing Nonexperimental Estimates of Impact against Experimental Estimates of Impact with Education Test Scores as Outcomes"](/doc/statistics/causality/2007-wilde.pdf "‘How close is close enough? Evaluating propensity score matching using data from a class size reduction experiment’, Wilde & Hollister 2007"), Wilde & Hollister 2002
> In this study we test the performance of some nonexperimental estimators of impacts applied to an educational intervention-reduction in class size-where achievement test scores were the outcome. We compare the nonexperimental estimates of the impacts to "true impact" estimates provided by a random-assignment design used to assess the effects of that intervention. Our primary focus in this study is on a nonexperimental estimator based on a complex procedure called propensity score matching. Previous studies which tested nonexperimental estimators against experimental ones all had employment or welfare use as the outcome variable. We tried to determine whether the conclusions from those studies about the performance of nonexperimental estimators carried over into the education domain.
>
> ...Project Star is the source of data for the experimental estimates and the source for drawing nonexperimental comparison groups used to make nonexperimental estimates. Project Star was an experiment in Tennessee involving 79 schools in which students in kindergarten through third grade were randomly assigned to small classes (the treatment group) or to regular-size classes (the control group). The outcome variables from the data set were the math and reading achievement test scores. We carried out the propensity-score-matching estimating procedure separately for each of 11 schools' kindergartens and used it to derive nonexperimental estimates of the impact of smaller class size. We also developed proper standard errors for the propensity-score-matched estimators by using bootstrapping procedures. We found that in most cases, the propensity-score estimate of the impact differed substantially from the "true impact" estimated by the experiment. We then attempted to assess how close the nonexperimental estimates were to the experimental ones. We suggested several different ways of attempting to assess "closeness." Most of them led to the conclusion, in our view, that the nonexperimental estimates were not very "close" and therefore were not reliable guides as to what the "true impact" was. We put greatest emphasis on looking at the question of "how close is close enough?" in terms of a decision-maker trying to use the evaluation to determine whether to invest in wider application of the intervention being assessed-in this case, reduction in class size. We illustrate this in terms of a rough cost-benefit framework for small class size as applied to Project Star. We find that in 30 to 45% of the 11 cases, the propensity-score-matching nonexperimental estimators would have led to the "wrong" decision.
>
> ...Two major considerations motivated us to undertake this study. First, four important studies (Fraker and Maynard, 1987; LaLonde, 1986; Friedlander and Robins, 1995; and Dehejia and Wahba, 1999) have assessed the effectiveness of nonexperimental methods of impact assessment in a compelling fashion, but these studies have focused solely on social interventions related to work and their impact on the outcome variables of earnings, employment rates, and welfare utilization.
>
> - Fraker & Maynard 1987, ["The adequacy of comparison group designs for evaluations of employment-related programs"](/doc/statistics/causality/1987-fraker.pdf "'The Adequacy of Comparison Group Designs for Evaluations of Employment-Related Programs', Fraker & Maynard 1987")
> - Friedlander & Robins 1995, ["Evaluating Program Evaluations: New Evidence on Commonly Used Nonexperimental Methods"](/doc/statistics/causality/1995-friedlander.pdf)
> - Dehejia & Wahba 1999 ["Causal effects in non-experimental studies: re-evaluating the evaluation of training programs"](/doc/statistics/causality/1999-dehejia.pdf "'Causal Effects in Nonexperimental Studies: Reevaluating the Evaluation of Training Programs', Dehejia & Wahba 1999")
>
> ...Because we are interested in testing nonexperimental methods on educational outcomes, we use Tennessee's Project Star as the source of the "true random-assignment" data. We describe Project Star in detail below. We use the treatment group data from a given school for the treatments and then construct comparison groups in various nonexperimental ways with data taken out of the control groups in other schools.
>
> ...1985–1989, researchers collected observational data including sex, age, race, and free-lunch status from over 11,000 students (Word, 1990). The schools chosen for the experiment were broadly distributed throughout Tennessee. Originally, the project included eight schools from nonmetropolitan cities and large towns (for example, Manchester and Maryville), 38 schools from rural areas, and 17 inner-city and 16 suburban schools drawn from four metropolitan areas: Knoxville, Nashville, Memphis, and Chattanooga. Beginning in 1985-86, the kindergarten teachers and students within Project Star classes were randomly assigned within schools to either "small" (13-17 pupils), "regular" (22-25), or "regular-with-aide" classes. New students who entered a Project Star school in 1986, 1987, 1988, or 1989 were randomly assigned to classes. Because each school had "the same kinds of students, curriculum, principal, policy, schedule, expenditures, etc, for each class" and the randomization occurred within school, theoretically, the estimated within-school effect of small classes should have been unbiased. During the course of the project, however, there were several deviations from the original experimental design-for example, after kindergarten the students in the regular and regular-with-aide classes were randomly reassigned between regular and regular-with-aide classes, and a significant number of students switched class types between grades. However, Krueger found that, after adjusting for these and other problems, the main Project Star results were unaffected; in all four school types students in small classes scored significantly higher on standardized tests than students in regular-size classes. In this study, following Krueger's example, test score is used as the measure of student achievement and is the outcome variable. For all comparisons, test score is calculated as a percentile rank of the combined raw Stanford Achievement reading and math scores within the entire sample distribution for that grade. The Project Star data set provides measures of a number of student, teacher, and school characteristics. The following are the variables available to use as measures prior to random assignment: student sex, student race, student free-lunch status, teacher race, teacher education, teacher career ladder, teacher experience, school type, and school system ID. In addition, the following variables measured contemporaneously can be considered exogenous: student age, assignment to small class size.
>
> ...One very important and stringent measure of closeness is whether there are many cases in which the nonexperimental impact estimates are opposite in sign from the experimental impact estimates and both sets of impact estimates are statistically-significantly different from 0, eg. the experimental estimates said that the mean test scores of those in smaller classes were significantly negative while the nonexperimental estimates indicated they were significantly positive. There is only one case in these 11 which comes close to this situation. For school 27, the experimental impact estimate is ! 10.5 and significant at the 6% level, just above the usual significance cutoff of 5%. The nonexperimental impact estimate is 35.2 and significant at better than the 1% level. In other cases (school 7 and school 33), the impact estimates are of opposite sign, but one or the other of them fails the test for being significantly different from 0. If we weaken the stringency of the criterion a bit, we can consider cases in which the experimental impact estimates were significantly different from 0 but the nonexperimental estimates were not (school 16 and school 33), or vice versa (schools 7, 16, and 28). Another, perhaps better, way of assessing the differences in the impact estimates is to look at column 8, which presents a test for whether the impact estimate from the nonexperimental procedure is significantly different from the impact estimate from the experimental procedure. For 8 of the 11 schools, the two impact estimates were statistically-significantly different from each other.
>
> ...When we first began considering this issue, we thought that a criterion might be based on the percentage difference in the point estimates of the impact. For example, for school 9 the nonexperimental estimate of the impact is 135% larger than the experimental impact. But for school 22 the nonexperimental impact estimate is 9% larger. Indeed, all but two of the nonexperimental estimates are more than 50% different from the experimental impact estimates. Whereas in this case the percentage difference in impact estimates seems to indicate quite conclusively that the nonexperimental estimates are not generally close to the experimental ones, in some cases such a percentage difference criterion might be misleading. The criterion which seems to us the most definitive is whether distance between the nonexperimental and the experimental impact estimates would have been sufficient to cause an observer to make a different decision from one based on the true experimental results. For example, suppose that the experimental impact estimate had been 0.02 and the nonexperimental impact estimate had been 0.04, a 100% difference in impact estimate. But further suppose that the decision about whether to take an action, eg. invest in the type of activity which the treatment intervention represents, would have been a yes if the difference between the treatments and comparisons had been 0.05 or greater and a no if the impact estimate had been less than 0.05. Then even though the nonexperimental estimate was 100% larger than the experimental estimate, one would still have decided not to invest in this type of intervention whether one had the true experimental estimate or the nonexperimental estimate.
>
> ...In a couple of his articles presenting aspects of his research using Project Star data, Krueger (1999, 2000) has developed some rough benefit-cost calculations related to reduction in class size. In Appendix B we sketch in a few elements of his calculations which provide the background for the summary measures derived from his calculations that we use to illustrate our "close enough." The benefits Krueger focuses on are increases in future earnings that could be associated with test score gains. He carefully develops estimates - based on other literature - of what increase in future earnings might be associated with a gain in test scores in the early years of elementary school. With appropriate discounting to present values, and other adjustments, he uses these values as estimates of benefits and then compares them to the estimated cost of reducing class size 22 → 15, taken from the experience in Project Star and appropriately adjusted. For our purposes, what is most interesting is the way he uses these benefit-cost calculations to answer a slightly different question: How big an effect on test scores due to reduction of class size 22 → 15 would have been necessary to just justify the expenditures it took to reduce the class size by that much? He states the answer in terms of "effect size," that is the impact divided by the estimated standard deviation of the impact. This is a measure that is increasingly used to compare across outcomes that are measured in somewhat different metrics. His answer is that an effect size of 0.2 of a standard deviation of tests scores would have been just large enough to generate estimated future earnings gains sufficient to justify the costs. 4 Krueger indicates that the estimated effect for kindergarten was a 5.37 percentile increase in achievement test scores due to smaller class size and that this was equivalent to 0.2 of a standard deviation in test scores. Therefore we use 5.4 percentile points as the critical value for a decision of whether the reduction in class size 22 → 15 would have been cost-effective. In Table 2 we use the results from Table 1 to apply the cost-effectiveness criterion to determine the extent to which the nonexperimental estimates might have led to the wrong decision. To create the entries in this table, we look at the Table 1 entry for a given school. If the impact estimate is greater than 5.4 percentile points and statistically-significantly different from 0, we enter a Yes, indicating the impact estimate would have led to a conclusion that reducing class size 22 → 15 was cost-effective. If the impact estimate is less than 5.4 or statistically not significantly different from 0, we enter a No to indicate a conclusion that the class-size reduction was not cost-effective. Column 1 is the school ID, column 2 gives the conclusion on the basis of the experimental impact estimate, column 3 gives the conclusion on the basis of the nonexperimental impact estimate, and column 4 contains an x if the nonexperimental estimate would have led to a "wrong" cost-effectiveness conclusion, ie. a different conclusion from the experimental impact conclusion about cost-effectiveness.
>
> It is easy to see in Table 2 that the nonexperimental estimate would have led to the wrong conclusion in four of the 11 cases. For a fifth case, school 16, we entered a Maybe in Column 4 because, as shown in Table 1, for that school the nonexperimental estimate was significantly different from 0 at only the 9% level, whereas the usual significance criterion is 5%. Even though the nonexperimental point estimate of impact was greater than 5.4 percentile points, strict use of the 5% significance criterion would have led to the conclusion that the reduction in class size was not cost-effective. On the other hand, analysts sometimes use a 10% significance criterion, so it could be argued that they might have used that level to conclude the program was cost-effective - thus the Maybe entry for this school.
>
> ...In all seven selected cases, the experimental and nonexperimental estimates differ considerably from each other. One of the nonexperimental estimates is of the wrong sign, while in the other estimates, the signs are the same but all the estimates differ by at least 1.8 percentage points, ranging up to as much as 12 percentage points (rural-city). Statistical inferences about the significance of these program effects also vary (five of the seven pairs had differing inferences-ie. only one estimate of the program effect in a pair is statistically-significant at the 10% level). All of the differences between the experimental and nonexperimental estimates (the test of difference between the outcomes for the experimental control group and the nonexperimental comparison group) in this subset were statistically-significant.
>
> Table 5 shows the results for the complete set of the first 49 pairs of estimates. Each column shows a different type of comparison (either school type or district type). The top row in each column provides the number of pairs of experimental and nonexperimental estimates in the column. The second row shows the mean estimate of program effect from the (unbiased) experimental estimates. The third row has the mean absolute differences between these estimates, providing some indication of the size of our nonexperimental bias. The fourth row provides the percentage of pairs in which the experimental and nonexperimental estimates led to different inferences about the significance of the program effect. The fifth row indicates the percentage of pairs in which the difference between the two estimated values was significant (again the test of difference between control and comparison group). Looking at the summarized results for comparisons across school type, these results suggest that constructing nonexperimental groups based on similar demographic school types leads to nonexperimental estimates that do not perform very well when compared with the experimental estimates for the same group. In 50% of the pairs, experimental and nonexperimental estimates had different statistical inferences, with a mean absolute difference in effect estimate of 4.65. Over 75% of these differences were statistically-significant. About half of the estimated pairs in comparisons across school type differ by more than 5 percentage points.
# Psychology
["Assignment Methods in Experimentation: When Do Nonrandomized Experiments Approximate Answers From Randomized Experiments?"](/doc/statistics/causality/1996-heinsman.pdf), Heinsman & Shadish 1996:
> This meta-analysis compares effect size estimates from 51 randomized experiments to those from 47 nonrandomized experiments. These experiments were drawn from published and unpublished studies of Scholastic Aptitude Test coaching, ability grouping of students within classrooms, presurgical education of patients to improve post-surgical outcome, and drug abuse prevention with juveniles. The raw results suggest that the two kinds of experiments yield very different answers. But when studies are equated for crucial features (which is not always possible), nonrandomized experiments can yield a reasonably accurate effect size in comparison with randomized designs. Crucial design features include the activity level of the intervention given the control group, pretest effect size, selection and attrition levels, and the accuracy of the effect-size estimation method. Implications of these results for the conduct of meta-analysis and for the design of good nonrandomized experiments are discussed.
>
> ...When certain assumptions are met (eg. no treatment correlated attrition) and it is properly executed (eg. assignment is not overridden), random assignment allows unbiased estimates of treatment effects and justifies the theory that leads to tests of significance. We compare this experiment to a closely related quasiexperimental design---the nonequivalent control group design - that is similar to the randomized experiment except that units are not assigned to conditions at random (Cook & Campbell, 1979).
>
> Statistical theory is mostly silent about the statistical characteristics (bias, consistency, and efficiency) of this design. However, meta-analysts have empirically compared the two designs. In meta-analysis, study outcomes are summarized with an effect size statistic (Glass, 1976). In the present case, the standardized mean difference statistic is relevant:
>
> _d_ = (mean treatment - mean control) / SD all
>
> where _A_⁄_T_ is the mean of the experimental group, _M~c~_ is the mean of the comparison group, and _SD~P~_ is the pooled standard deviation. This statistic allows the meta-analyst to combine study outcomes that are in disparate metrics into a single metric for aggregation. Comparisons of effect sizes from randomized and nonrandomized experiments have yielded inconsistent results (eg. Becker, 1990; Colditz, Miller, & Mosteller, 1988; Hazelrigg, Cooper, & Borduin, 1987; Shapiro & Shapiro, 1983; Smith, Glass & Miller, 1980). A recent summary of such work (Lipsey & Wilson, 1993) aggregated the results of 74 meta-analyses that reported separate standardized mean difference statistics for randomized and nonrandomized studies. Overall, the randomized studies yielded an average standardized mean difference statistic of _d_ = 0.46 (SD = 0.28), trivially higher than the nonrandomized studies _d_ = 0.41 (SD = 0.36); that is, the difference was near zero on the average over these 74 meta-analyses. Lipsey & Wilson 1993 concluded that "there is no strong pattern or bias in the direction of the difference made by lower quality methods. In a given treatment area, poor design or low methodological quality may result in a treatment estimate quite discrepant from what a better quality design would yield, but it is almost as likely to be an underestimate as an overestimate" (p. 1193). However, we believe that considerable ambiguity still remains about this methodological issue.
>
> - Becker, B. J. (1990). ["Coaching for the Scholastic Aptitude Test: Further synthesis and appraisal"](/doc/statistics/causality/1990-baker.pdf). _Review of Educational Research_, 60, 373-417
> - Colditz, G. A., Miller, J. N., & Mosteller, F. (1988). ["The effect of study design on gain in evaluation of new treatments in medicine and surgery"](/doc/statistics/causality/1988-colditz.pdf). _Drug Information Journal_, 22, 343-352
> - Hazelrigg, M. D., Cooper, H. M., & Borduin, C. M. (1987). ["Evaluating the effectiveness of family therapies: An integrative review and analysis"](/doc/statistics/causality/1987-hazelrigg.pdf). _Psychological Bulletin_, 101, 428-442
> - Lipsey, M. W., & Wilson, D. B. (1993). ["The efficacy of psychological, educational, and behavioral treatment: Confirmation from meta-analysis"](/doc/psychology/1993-lipsey.pdf "'The Efficacy of Psychological, Educational, and Behavioral Treatment: Confirmation from Meta-Analysis', Lipsey & Wilson 1993"){#lipsey-wilson-1993-2}. _American Psychologist_, 48, 1181-1209.
> - Shapiro, D. A., & Shapiro, D. (1983). ["Comparative therapy outcome research: Methodological implications of meta-analysis"](/doc/statistics/causality/1983-shapiro.pdf). _Journal of Consulting and Clinical Psychology_, 51, 42-53.
> - Smith et al 1980, [_The benefits of psychotherapy_](/doc/psychology/1980-smith-thebenefitsofpsychotherapy.pdf). Baltimore: Johns Hopkins University Press. [followup to [the 1977 paper](/doc/psychology/1977-smith.pdf "'Meta-Analysis of Psychotherapy Outcome Studies', Smith & Glass 1977")? paper doesn't include anything about randomization as a covariate. Ordered used copy; book mentions issue but only notes that there is no large average effect difference; does not provide original data! An entire book and they can't include the coded-up data which would be impossible to reproduce at this date... TODO: ask around if there are any archives anywhere - maybe University of Colorado has the original data in Smith or Glass's archived papers?]
>
> ...The present study drew from four past meta-analyses that contained both random and nonrandomized experiments on juvenile drug use prevention programs (Tobler, 1986), psychosocial interventions for post-surgery outcomes (Devine, 1992), coaching for Scholastic Aptitude Test performance (Becker, 1990), and ability grouping of pupils in secondary school classes (Slavin, 1990). These four areas were selected deliberately to reflect different kinds of interventions and substantive topics.
> ...All four meta-analyses also included many unpublished manuscripts, allowing us to examine publication bias effects. In this regard, a practical reason for choosing these four was that previous contacts with three of the four authors of these meta-analyses suggested that they would be willing to provide us with these unpublished documents.
>
> ...This procedure yielded 98 studies for inclusion, 51 random and 47 nonrandom. These studies allowed computation of 733 effect sizes, which we aggregated to 98 study-level effect sizes. Table 1 describes the number of studies in more detail. Retrieving equal numbers of published and unpublished studies in each cell of Table 1 proved impossible. Selection criteria resulted in elimination of 103 studies, of which 40 did not provide enough statistics to calculate at least one good effect size; 119 reported data only for significant effects but not for non-statistically-significant ones; 15 did not describe assignment method adequately; 11 reported only dichotomous outcome measures; 9 used haphazard assignment; 5 had no control group; and 4 were eliminated for other reasons (extremely implausible data, no posttest reported, severe unit of analysis problem, or failure to report any empirical results).
>
> ...Table 2 shows that over all 98 studies, experiments in which subjects were randomly assigned to conditions yielded significantly larger effect sizes than did experiments in which random assignment did not take place (Q = 82.09, df=l, _p_ < 0.0001). Within area, randomized experiments yielded significantly more positive effect sizes for ability grouping (Q = 4.76, df = 1, _p_ = 0.029) and for drug-use prevention studies (Q = 15.67, df = 1, _p_ = 0.000075) but not for SAT coaching (Q = 0.02, df = I, _p_ = 0.89) and presurgical intervention studies (Q = 0.17, df=\,_p_ = 0.68). This yielded a borderline interaction between assignment mechanism and substantive area (Q = 5.93, df = 3, _p_ = 0.12). We include this interaction in subsequent regressions because power to detect interactions is smaller than power to detect main effects and because such an interaction is conceptually the same as Lipsey and Wilson's (1993) finding that assignment method differences may vary considerably over substantive areas. Finally, as Hedges (1983) predicted, the variance component for nonrandomized experiments was twice as large as the variance component for randomized experiments in the overall sample. Within areas, variance components were equal in two areas but larger for nonrandomized experiments in two others. Hence nonrandom assignment may result in unusually disparate effect size estimates, creating different means and variances.
>
> - Hedges, L. V. (1983). ["A random effects model for effect sizes"](/doc/statistics/causality/1983-hedges.pdf). _Psychological Bulletin_, 93, 388-395
>
> ...Effect size was higher with low differential and total attrition, with passive controls, with higher pretest effect sizes, when the selection mechanism did not involve self-selection of subjects into treatment, and with exact effect size computation measures.
>
> ...*Projecting the Results of an Ideal Comparison*:
> Given these findings, one might ask what an ideal comparison between randomized and nonrandomized experiments would yield. We simulate such a comparison in Table 6 using the results in Table 5, projecting effect sizes using predictor values that equate studies at an ideal or a reasonable level. The projections in Table 6 assume that both randomized and nonrandomized experiments used passive control groups, internal control groups, and matching; allowed exact computation of _d_; had no attrition; standardized treatments; were published; had pretest effect sizes of zero; used _n_ = 1,000 subjects per study; did not allow self-selection of subjects into conditions; and used outcomes based on self-reports and specifically tailored to treatment. Area effects and interaction effects between area and assignment were included in the projection. Note that the overall difference among the eight cell means has diminished dramatically in comparison with Table 2. In Table 2, the lowest cell mean was -0.23 and the highest was 0.37, for a range of 0.60. The range in Table 6 is only half as large (0.34). The same conclusion is true for the range within each area. In Table 2 that range was 0.01 for the smallest difference between randomized and nonrandomized experiments (SAT coaching) to 0.21 for the largest difference (drug-use prevention). In Table 6, the range was 0.11 (SAT coaching), 0.01 (ability grouping), 0.05 (presurgical interventions), and 0.09 (drug-use prevention). Put a bit more simply, nonrandomized experiments are more like randomized experiments if one takes confounds into account.
["Comparison of evidence of treatment effects in randomized and nonrandomized studies"](/doc/statistics/causality/2001-ioannidis.pdf "'Comparison of Evidence of Treatment Effects in Randomized and Nonrandomized Studies', Ioannidis et al 2001"), Ioannidis et al 2001:
> *Study Selection*: 45 diverse topics were identified for which both randomized trials (_n_ = 240) and nonrandomized studies (_n_ = 168) had been performed and had been considered in meta-analyses of binary outcomes.
>
> *Data Extraction*: Data on events per patient in each study arm and design and characteristics of each study considered in each meta-analysis were extracted and synthesized separately for randomized and nonrandomized studies.
>
> *Data Synthesis*: Very good correlation was observed between the summary odds ratios of randomized and nonrandomized studies (_r_= 0.75; _p_ < .001); however, non-randomized studies tended to show larger treatment effects (28 vs 11; _p_ = 0.009). Between-study heterogeneity was frequent among randomized trials alone (23%) and very frequent among nonrandomized studies alone (41%). The summary results of the 2 types of designs differed beyond chance in 7 cases (16%). Discrepancies beyond chance were less common when only prospective studies were considered (8%). Occasional differences in sample size and timing of publication were also noted between discrepant randomized and nonrandomized studies. In 28 cases (62%), the natural logarithm of the odds ratio differed by at least 50%, and in 15 cases (33%), the odds ratio varied at least 2-fold between nonrandomized studies and randomized trials.
>
> *Conclusions*: Despite good correlation between randomized trials and nonrandomized studies - in particular, prospective studies - discrepancies beyond chance do occur and differences in estimated magnitude of treatment effect are very common.
["Comparison of Effects in Randomized Controlled Trials With Observational Studies in Digestive Surgery"](/doc/statistics/causality/2006-shikata.pdf), Shikata et al 2006:
> *Methods*: The PubMed (1966 to April 2004), Embase (1986 to April 2004) and Cochrane databases (Issue 2, 2004) were searched to identify meta-analyses of randomized controlled trials in digestive surgery. Fifty-two outcomes of 18 topics were identified from 276 original articles (96 randomized trials, 180 observational studies) and included in meta-analyses. All available binary data and study characteristics were extracted and combined separately for randomized and observational studies. In each selected digestive surgical topic, summary odds ratios or relative risks from randomized controlled trials were compared with observational studies using an equivalent calculation method.
>
> *Results*: Significant between-study heterogeneity was seen more often among observational studies (5 of 12 topics) than among randomized trials (1 of 9 topics). In 4 of the 16 primary outcomes compared (10 of 52 total outcomes), summary estimates of treatment effects showed significant discrepancies between the two designs.
>
> *Conclusions*: One fourth of observational studies gave different results than randomized trials, and between-study heterogeneity was more common in observational studies in the field of digestive surgery.
["A Comparison of Approaches to Advertising Measurement: Evidence from Big Field Experiments at Facebook"](/doc/statistics/causality/2019-gordon.pdf), Gordon et al 2019:
> We examine how common techniques used to measure the causal impact of ad exposures on users' conversion outcomes compare to the "gold standard" of a true experiment (randomized controlled trial). Using data from 12 US advertising lift studies at Facebook comprising 435 million user-study observations and 1.4 billion total impressions we contrast the experimental results to those obtained from observational methods, such as comparing exposed to unexposed users, matching methods, model-based adjustments, synthetic matched-markets tests, and before-after tests. We show that observational methods often fail to produce the same results as true experiments even after conditioning on information from thousands of behavioral variables and using non-linear models. We explain why this is the case. Our findings suggest that common approaches used to measure advertising effectiveness in industry fail to measure accurately the true effect of ads.
>
> ...Figure 13 summarizes results for the four studies for which there was a conversion pixel on a registration page. Figure 14 summarizes results for the three studies for which there was a conversion pixel on a key landing page. The results for these studies vary across studies in how they compare to the RCT results, just as they do for the checkout conversion studies reported in Figures 11 and 12.
>
> We summarize the performance of different observational approaches using two different metrics. We want to know first how often an observational study fails to capture the truth. Said in a statistically precise way, "For how many of the studies do we reject the hypothesis that the lift of the observational method is equal to the RCT lift?" Table 7 reports the answer to this question. We divide the table by outcome reported in the study (checkout is in the top section of Table 7, followed by registration and page view). The first row of Table 7 tells us that of the 11 studies that tracked checkout conversions, we statistically reject the hypothesis that the exact matching estimate of lift equals the RCT estimate. As we go down the column, the propensity score matching and regression adjustment approaches fare a little better, but for all but one specification, we reject equality with the RCT estimate for half the studies or more.
>
> We would also like to know how different the estimate produced by an observational method is from the RCT estimate. Said more precisely, we ask "Across evaluated studies of a given outcome, what is the average absolute deviation in percentage points between the observational method estimate of lift and the RCT lift?" For example, the RCT lift for study 1 (checkout outcome) is 33%. The EM lift estimate is 117%. Hence the absolute lift deviation is 84 percentage points. For study 2 (checkout outcome) the RCT lift is 0.9%, the EM lift estimate is 535%, and the absolute lift deviation is 534 percentage points. When we average over all studies, exact matching leads to an average absolute lift deviation of 661 percentage points relative to an average RCT lift of 57% across studies (see the last two columns of the first row of the table.)
["Measuring Consumer Sensitivity to Audio Advertising: A Field Experiment on Pandora Internet Radio"](https://davidreiley.com/papers/PandoraListenerDemandCurve.pdf), Huang et al 2018:
> How valuable is the variation generated by this experiment? Since it can be difficult to convince decision makers to run experiments on key economic decisions, and it consumes engineering resources to implement such an experiment properly, could we have done just as well by using observational data? To investigate this question, we re-run our analysis using only the 17 million listeners in the control group, since they were untouched by the experiment in the sense that they received the default ad load. In the absence of experimental instrumental variables, we run the regression based on naturally occurring variation in ad load, such as that caused by higher advertiser demand for some listeners than others, excluding listeners who got no ads during the experimental period.
>
> The results are found in Table 7. We find that the endogeneity of the realized ad load (some people get more ad load due to advertiser demand, and these people happen to listen less than people with lower advertiser demand) causes us to overestimate the true causal impact of ad load by a factor of approximately 4.
>
> ...To give the panel estimator its best shot, we use what we have learned from the experiment, and allow the panel estimator a 20-month time period between observations...We see from Table 8 that the point estimate for active days is much closer to that found in Table 5, but it still overestimates the impact of ad load by more than the width of our 95% confidence intervals. The panel point estimate for total hours, while an improvement over the cross-sectional regression results, still overestimates the effect by a factor of 3. Our result suggests that, even after controlling for time-invariant listener heterogeneity, observational techniques still suffer from omitted-variable bias caused by unobservable terms that vary across individuals *and* time that correlate with ad load and listening behaviors. And without a long-run experiment, we would not have known the relevant timescale to consider to measure the long-run sensitivity to advertising (which is what matters for the platform's policy decisions)
# Education
["An evaluation of bias in three measures of teacher quality: Value-added, classroom observations, and student surveys"](https://scholar.harvard.edu/files/andrewbacherhicks/files/an_evaluation_of_bias_in_three_measures_of_teacher_quality.pdf), Bacher-Hicks et al 2017:
> We conduct a random assignment experiment to test the predictive validity of three measures of teacher performance: value added, classroom observations, and student surveys. Combining our results with those from two previous random assignment experiments, we provide further(and more precise) evidence that value-added measures are unbiased predictors of teacher performance. In addition, we provide the first evidence that classroom observation scores are unbiased predictors of teacher performance on a rubric measuring the quality of mathematics instruction, but we lack the statistical power to reach any similar conclusions for student survey responses.
> We used the pre-existing administrative records and the additional data collected by NCTE to generate estimates of teacher performance on five measures: (a) students' scores on state standardized mathematics tests; (b) students' scores on the project-developed mathematics test (Hickman, Fu, & Hill, 2012); (c) teachers' performance on the Mathematical Quality of Instruction (MQI; Hill et al 2008) classroom observation instrument; (d) teachers' performance on the Classroom Assessment Scoring System (CLASS; La Paro, Pianta, & Hamre, 2012) observation instrument; and(e)students' responses to a Tripod-based perception survey (Ferguson, 2009).5 Kane & Staiger 2008 McCaffrey, Miller, and Staiger (2013)
["Validating Teacher Effects On Students' Attitudes And Behaviors: Evidence From Random Assignment Of Teachers To Students"](/doc/statistics/causality/2017-blazar.pdf), Blazar 2017:
> There is growing interest among researchers, policymakers, and practitioners in identifying teachers who are skilled at improving student outcomes beyond test scores. However, important questions remain about the validity of these teacher effect estimates. Leveraging the random assignment of teachers to classes, I find that teachers have causal effects on their students' self-reported behavior in class, self-efficacy in math, and happiness in class that are similar in magnitude to effects on math test scores. Weak correlations between teacher effects on different student outcomes indicate that these measures capture unique skills that teachers bring to the classroom. Teacher effects calculated in non-experimental data are related to these same outcomes following random assignment, revealing that they contain important information content on teachers. However, for some non-experimental teacher effect estimates, large and potentially important degrees of bias remain. These results suggest that researchers and policymakers should proceed with caution when using these measures. They likely are more appropriate for low-stakes decisions, such as matching teachers to professional development, than for high-stakes personnel decisions and accountability.
>
> ...In Table 5, I report estimates describing the relationship between non-experimental teacher effects on student outcomes and these same measures following random assignment. Cells contain estimates from separate regression models where the dependent variable is the student attitude or behavior listed in each column. The independent variable of interest is the non-experimental teacher effect on this same outcome estimated in years prior to random assignment. All models include fixed effects for randomization block to match the experimental design. In order to increase the precision of my estimates, models also control for students' prior achievement in math and reading, student demographic characteristics, and classroom characteristics from randomly assigned rosters.
>
> ...Validity evidence for teacher effects on students' math performance are consistent with other experimental studies (Kane et al 2013; Kane and Staiger 2008), where predicted differences in teacher effectiveness in observational data come close to actual differences following random assignment of teachers to classes. The non-experimental teacher effect estimate that comes closest to a 1:1 relationship is the shrunken estimate that controls for students' prior achievement and other demographic characteristics (0.995 SD).
>
> Despite a relatively small sample of teachers, the standard error for this estimate (0.084) is substantively smaller than those in other studies---including the meta-analysis conducted by Bacher-Hicks et al 2017---and allows me to rule out relatively large degrees of bias in teacher effects calculated from this model. A likely explanation for greater precision in this study relative to others is the fact that other studies generate estimates through instrumental variables estimation to calculate treatment on the treated. Instead, I use OLS regression and account for non-compliance by narrowing in on randomization blocks in which very few, in any, students moved out of their randomly assigned teachers' classroom. Non-experimental teacher effects calculated without shrinkage are related less strongly to current student outcomes, though differences in estimates and associated standard errors between Panel A and Panel B are not large. All corresponding estimates (eg. Model 1 from Panel A versus Panel B) have overlapping 95% confidence intervals.
>
> ...For both Self-Efficacy in Math and Happiness in Class, non-experimental teacher effect estimates have moderate predictive validity. Generally, I can distinguish estimates from 0 SD, indicating that they contain some information content on teachers. The exception is shrunken estimates for Self-Efficacy in Math. Although estimates are similar in magnitude to the unshrunken estimates in Panel A, between 0.42 SD and 0.58 SD, standard errors are large and 95% confidence intervals cross 0 SD. I also can distinguish many estimates from 1 SD. This indicates that non-experimental teacher effects on students' Self-Efficacy in Math and Happiness in Class contain potentially large and important degrees of bias. For both measures of teacher effectiveness, point estimates around 0.5 SD suggest that they contain roughly 50% bias.
>
> !["**Table 5**: Relationship between Current Student Outcomes and Prior, Non-experimental Teacher Effect Outcomes" [3⁄4 effects <1 imply bias]](/doc/statistics/causality/2017-blazar-table5-correlationvscausation.png){.width-full .invert}
# TODO
- Lonn EM, Yusuf S. "Is there a role for antioxidant vitamins in the prevention of cardiovascular disease? An update on epidemiological and clinical trials data". _Can J Cardiol_ 1997;13:957-965
- Patterson RE, White E, Kristal AR, Neuhouser ML, Potter JD. "Vitamin supplement and cancer risk: the epidemiological evidence". _Cancer Causes Control_ 1997;8:786-802
- "Comparisons of effect sizes derived from randomized and non-randomised studies", BC Reeves, RR MacLehose, IM Harvey, TA Sheldon... - _Health Services Research_ ..., 1998 [superseded by MacLehose et al 2000?]
- Glazerman, S., Levy, D., & Myers, D. (2002). [_Nonexperimental replications of social experiments: A systematic review_](https://www.mathematica.org/-/media/publications/pdfs/nonexperimentalreps.pdf). Washington, DC: Mathematica Policy Research
- Bloom, H. S., Michalopoulos, C., Hill, C., & Lei, Y. (2002) [_Can non-experimental comparison group methods match the findings from a random assignment evaluation of mandatory welfare-to-work programs?_](#bloom-et-al-2002) New York: Manpower Demonstration Research Corporation.
- Fraker & Maynard 1987, ["The adequacy of comparison group designs for evaluations of employment-related programs"](/doc/statistics/causality/1987-fraker.pdf "'The Adequacy of Comparison Group Designs for Evaluations of Employment-Related Programs', Fraker & Maynard 1987"){#fraker-maynard-1987-2}
- Friedlander & Robins 1995, ["Evaluating Program Evaluations: New Evidence on Commonly Used Nonexperimental Methods"](/doc/statistics/causality/1995-friedlander.pdf)
- Dehejia and Wahba, 1999 ["Causal effects in non-experimental studies: re-evaluating the evaluation of training programs"](/doc/statistics/causality/1999-dehejia.pdf "'Causal Effects in Nonexperimental Studies: Reevaluating the Evaluation of Training Programs', Dehejia & Wahba 1999"){#dehejia-wahba-1999-2}
- Becker, B. J. (1990). ["Coaching for the Scholastic Aptitude Test: Further synthesis and appraisal"](/doc/statistics/causality/1990-baker.pdf). _Review of Educational Research_, 60, 373-417
- Hazelrigg, M. D., Cooper, H. M., & Borduin, C. M. (1987). ["Evaluating the effectiveness of family therapies: An integrative review and analysis"](/doc/statistics/causality/1987-hazelrigg.pdf). _Psychological Bulletin_, 101, 428-442
- Lipsey, M. W., & Wilson, D. B. (1993). ["The efficacy of psychological, educational, and behavioral treatment: Confirmation from meta-analysis"](/doc/psychology/1993-lipsey.pdf "'The Efficacy of Psychological, Educational, and Behavioral Treatment: Confirmation from Meta-Analysis', Lipsey & Wilson 1993"){#lipsey-wilson-1993-3}. _American Psychologist_, 48, 1181-1209.
- Shapiro, D. A., & Shapiro, D. (1983). ["Comparative therapy outcome research: Methodological implications of meta-analysis"](/doc/statistics/causality/1983-shapiro.pdf). _Journal of Consulting and Clinical Psychology_, 51, 42-53.
- Hedges, L. V. (1983). ["A random effects model for effect sizes"](/doc/statistics/causality/1983-hedges.pdf). _Psychological Bulletin_, 93, 388-395