The Kelly Coin-Flipping Game: Exact Solutions
Decision-theoretic analysis of how to optimally play the Haghani & Dewey 2016 300-round double-or-nothing coin-flipping game with an edge and ceiling better than using the Kelly Criterion. Computing and following an exact decision tree increases earnings by $6.6 over a modified KC.
2016 experiment with a double-or-nothing coin-flipping game where the player starts with $25 (ie. $35.79$252016) and has an edge of 60%, and can play 300 times, choosing how much to bet each time, winning up to a maximum ceiling of $250. Most of their subjects fail to play well, earning an average $91, compared to the 2016 heuristic benchmark of ~$240 in winnings achievable using a modified Kelly Criterion as their strategy. The KC, however, is not optimal for this problem as it ignores the ceiling and limited number of plays.
We solve the problem of the value of optimal play exactly by using decision trees & dynamic programming for calculating the value function, with implementations in R, Haskell, and C. (See also Problem #14.) We also provide a closed-form exact value formula in R & Python, several approximations using Monte Carlo/random forests/neural networks, visualizations of the value function, and a Python implementation of the game for the OpenAI Gym collection.
We find that optimal play yields $246.61 on average (rather than ~$240), and so the human players actually earned only 36.8% of what was possible, losing $155.6 in potential profit. Comparing decision trees and the Kelly criterion for various horizons (bets left), the relative advantage of the decision tree strategy depends on the horizon: it is highest when the player can make few bets (at b = 23, with a difference of ~$36), and decreases with number of bets as more strategies hit the ceiling.
In the Kelly game, the maximum winnings, number of rounds, and edge are fixed; we describe a more difficult generalized version in which the 3 parameters are drawn from Pareto, normal, and beta distributions and are unknown to the player (who can use Bayesian inference to try to estimate them during play). Upper and lower bounds are estimated on the value of this game. In the variant of this game where subjects are not told the exact edge of 60%, a Bayesian decision tree approach shows that performance can closely approach that of the decision tree, with a penalty for 1 plausible prior of only $1.
Two deep reinforcement learning agents, DQN & DDPG, are implemented but DQN fails to learn and DDPG doesn’t show acceptable performance with default settings, indicating better tuning may be required for them to solve the generalized Kelly game.
The paper “Rational Decision-Making Under Uncertainty: Observed Betting Patterns on a Biased Coin”, by 2016 runs an economics/psychology experiment on optimal betting in a simple coin-flipping game:
What would you do if you were invited to play a game where you were given $35.79$252016 and allowed to place bets for 30 minutes on a coin that you were told was biased to come up heads 60% of the time? This is exactly what we did, gathering 61 young, quantitatively trained men and women to play this game.
The results, in a nutshell, were that the majority of these 61 players didn’t place their bets well, displaying a broad panoply of behavioral and cognitive biases. About 30% of the subjects actually went bust, losing their full $35.79$252016 stake. We also discuss optimal betting strategies, valuation of the opportunity to play the game and its similarities to investing in the stock market.
The main implication of our study is that people need to be better educated and trained in how to approach decision making under uncertainty. If these quantitatively trained players, playing the simplest game we can think of involving uncertainty and favourable odds, didn’t play well, what hope is there for the rest of us when it comes to playing the biggest and most important game of all: investing our savings? In the words of Ed Thorp, who gave us helpful feedback on our research: “This is a great experiment for many reasons. It ought to become part of the basic education of anyone interested in finance or gambling.”
More specifically:
…Prior to starting the game, participants read a detailed description of the game, which included a clear statement, in bold, indicating that the simulated coin had a 60% chance of coming up heads and a 40% chance of coming up tails. Participants were given $35.79$252016 of starting capital and it was explained in text and verbally that they would be paid, by check, the amount of their ending balance subject to a maximum payout. The maximum payout would be revealed if and when subjects placed a bet that if successful would make their balance greater than or equal to the cap. We set the cap at $357.92$2502016…Participants were told that they could play the game for 30 minutes, and if they accepted the $35.79$252016 stake, they had to remain in the room for that amount of time.5 Participants could place a wager of any amount in their account, in increments of $0.01$0.012016, and they could bet on heads or tails…Assuming a player with agile fingers can put down a bet every 6 seconds, that would allow 300 bets in the 30 minutes of play.
Near-Optimal Play
The authors make a specific suggestion about what near-optimal play in this game would be, based on the Kelly criterion which would yield bets each round of 20% of capital:
The basic idea of the Kelly formula is that a player who wants to maximize the rate of growth of his wealth should bet a constant fraction of his wealth on each flip of the coin, defined by the function (2 × p) − 1, where p is the probability of winning. The formula implicitly assumes the gambler has log utility. It’s intuitive that there should be an optimal fraction to bet; if the player bets a very high fraction, he risks losing so much money on a bad run that he would not be able to recover, and if he bet too little, he would not be making the most of what is a finite opportunity to place bets at favorable odds…We present the Kelly criterion as a useful heuristic a subject could gainfully employ. It may not be the optimal approach for playing the game we presented for several reasons. The Kelly criterion is consistent with the bettor having log-utility of wealth, which is a more tolerant level of risk aversion than most people exhibit. On the other hand, the subjects of our experiment likely did not view $35.79$252016 (or even $357.92$2502016) as the totality of their capital, and so they ought to be less risk averse in their approach to maximizing their harvest from the game. The fact that there is some cap on the amount the subject can win should also modify the optimal strategy…In our game, the Kelly criterion would tell the subject to bet 20% () of his account on heads on each flip. So, the first bet would be $5 (20% of $25) on heads, and if he won, then he’d bet $6 on heads (20% of $30), but if he lost, he’d bet $4 on heads (20% of $20), and so on.
…If the subject rightly assumed we wouldn’t be offering a cap of more than $1,000 per player, then a reasonable heuristic would be to bet a constant proportion of one’s bank using a fraction less than the Kelly criterion, and if and when the cap is discovered, reducing the betting fraction further depending on betting time remaining to glide in safely to the maximum payout. For example, betting 10% or 15% of one’s account may have been a sound starting strategy. We ran simulations on the probability of hitting the cap if the subject bet a fixed proportion of wealth of 10%, 15% and 20%, and stopping when the cap was exceeded with a successful bet. We found there to be a 95% probability that the subjects would reach the $250 cap following any of those constant proportion betting strategies, and so the expected value of the game as it was presented (with the $250 cap) would be just under $240. However, if they bet 5% or 40% of their bank on each flip, the probability of exceeding the cap goes down to about 70%.
This game is interesting as a test case because it is just easy enough to solve exactly on a standard computer in various ways, but also hard enough to defeat naive humans and be nontrivial.
Subjects’ Performance
Despite the Kelly criterion being well-known in finance and fairly intuitive, and the game being very generous, participants did not perform well:
The sample was largely comprised of college age students in economics and finance and young professionals at finance firms. We had 14 analyst and associate level employees at two leading asset management firms. The sample consisted of 49 males and 12 females. Our prior was that these participants should have been well prepared to play a simple game with a defined positive expected value…Only 21% of participants reached the maximum payout of $250,7 well below the 95% that should have reached it given a simple constant percentage betting strategy of anywhere from 10% to 20%.8 We were surprised that one third of the participants wound up with less money in their account than they started with. More astounding still is the fact that 28% of participants went bust and received no payout. That a game of flipping coins with an ex-ante 60:40 winning probability produced so many subjects that lost everything is startling. The average ending bankroll of those who did not reach the maximum and who also did not go bust, which represented 51% of the sample, was $75. While this was a tripling of their initial $25 stake, it still represents a very sub-optimal outcome given the opportunity presented. The average payout across all subjects was $91, letting the authors off the hook relative to the $250 per person they’d have had to pay out had all the subjects played well.
This is troubling because the problem is so well-defined and favorable to the players, and can be seen as a microcosm of the difficulties people experience in rational betting. (While it’s true that human subjects typically perform badly initially in games like the iterated prisoner’s dilemma and need time to learn, it’s also true that humans only have one life to learn stock market investment during, and these subjects all should’ve been well-prepared to play.)
Instead of expected earnings of ~$240, the players earned $91—forfeiting $149. However, if anything, the authors understate the underperformance, because as they correctly note, the Kelly criterion is not guaranteed to be optimal in this problem due to the potential for different utility functions (what if we simply want to maximize expected wealth, not log wealth?), the fixed number of bets & the ceiling, as the Kelly criterion tends to assume that wealth can increase without limit & there is an indefinite time horizon.
Optimality in the Coin-Flipping MDP
Indeed, we can see with a simple example that KC is suboptimal in terms of maximizing expected value: what if we are given only 1 bet (b = 1) to use our $25 on? If we bet 20% (or less) per the KC, then
0.6 × (25 + 5) + 0.4 × (25 − 5) = 26But if we bet everything:
0.6 × (25 + 25) + 0.4 × (25 − 25) = 30It’s true that 40% of the time, we go bankrupt and so we couldn’t play again… but there are no more plays in b = 1 so avoiding bankruptcy boots nothing.
We can treat this coin-flipping game as a tree-structured Markov decision process. For more possible bets, the value of a bet of a particular amount given a wealth w and bets remaining b-1 will recursively depend on the best strategy for the two possible outcomes (weighted by probability), giving us a Bellman value equation to solve like:
To solve this equation, we can explore all possible sequences of bets and outcomes to a termination condition and reward, and then work use backwards induction, defining a decision tree which can be (reasonably) efficiently computed using memoization/dynamic programming.
Given the problem setup, we can note a few things about the optimal strategy:
if the wealth ever reaches $0, the game has effectively ended regardless of how many bets remain, because betting $0 is the only possibility and it always returns $0
similarly, if the wealth ever reaches the upper bound of $250, the optimal strategy will effectively end the game by always betting $0 after that regardless of how many bets remain, since it can’t do better than $250 and can only do worse.
These two shortcuts will make the tree much easier to evaluate because many possible sequences of bet amounts & outcomes will quickly hit $0 or $250 and require no further exploration.
a state with more bets is always of equal or better value than fewer
a state with more wealth is always equal or better value than less
the value of 0 bets is the current wealth
the value of 1 bet depends on the ceiling and current wealth: whether $250 is >2× current wealth. If the ceiling more than twice current wealth, the optimal strategy with 1 bet left is to bet everything, since that has highest EV and there’s no more bets to worry about going bankrupt & missing out on.
Implementation of Game
A Python implementation (useful for applying the many reinforcement learning agent implementations which are Gym-compatible) is available in OpenAI Gym:
import gym
env = gym.make('KellyCoinflip-v0')
env.reset()
env._step(env.wealth*100*0.2) # bet with 20% KC
# ...
env._reset() # end of game, start a new one, etcDecision Tree
We can write down the value function as a mutual recursion: f calculates the expected value of the current step, and calls V to estimate the value of future steps; V checks for the termination conditions w=$0/$250 & b = 0 returning current wealth as the final payoff, and if not, calls f on every possible action to estimate their value and returns the max… This mutual recursion bottoms out at the termination conditions. As defined, this is grossly inefficient as every node in the decision tree will be recalculated many times despite yielding identical deterministic, referentially transparent results. So we need to memoize results if we want to evaluate much beyond b = 5.
Approximate Value Function
Implemented in R:
# devtools::install_github("hadley/memoise")
library(memoise)
f <- function(x, w, b) { 0.6*mV(min(w+x,250), b-1) + 0.4*mV(w-x, b-1)}
mf <- memoise(f)
V <- function(w,b) {
returns <- if (b>0 && w>0 && w<250) { sapply(seq(0, w, by=0.1), function(x) { mf(x,w,b) }) } else { w }
max(returns) }
mV <- memoise(V)
## sanity checks:
mV(25, 0) == 25 && mV(25, 1) == 30 && mV(0, 300) == 0Given our memoized value function mV we can now take a look at expected value of optimal betting for bets b 0–300 with the fixed starting payroll of $25. Memoization is no panacea, and R/memoise is slow enough that I am forced to make one change to the betting: instead of allowing bets in penny/$0.01 increments, I approximate by only allowing bets in $1 increments, to reduce the branching factor to a maximum of 250 possible choices each round rather than 25000 choices. (Some comparisons with decipenny and penny trees suggests that this makes little difference since early on the bet amounts are identical and later on being able to make <$1 adjustments to bets yield small gains relative to total wealth; see the Haskell implementation.)
Of course, even with memoization and reducing the branching factor, it’s still difficult to compute the value of the optimal strategy all the way to b = 300 because the exponentially increasing number of strategies still need to be computed at least once. With this R implementation, trees for up to b = 150 can be computed with 4GB RAM & ~16h.
The value function for increasing bets:
vs <- sapply(1:150, function(b) { round(mV(25, b), digits=1) }); vs
# [1] 30.0 36.0 43.2 45.4 48.0 53.7 54.6 57.6 61.8 62.6 66.8 68.2 70.6 74.1 75.0 79.1 79.7 82.5 84.7 86.2 89.8 90.3 93.8
# [24] 94.5 97.0 98.8 100.3 103.2 103.9 107.2 107.6 110.3 111.4 113.3 115.2 116.4 119.0 119.6 122.4 122.9 125.3 126.2 128.1 129.5 130.8 132.8
# [47] 133.6 136.0 136.5 138.8 139.4 141.4 142.3 143.8 145.2 146.3 148.0 148.8 150.6 151.3 153.1 153.8 155.5 156.3 157.7 158.8 159.9 161.2 162.1
# [70] 163.6 164.2 165.8 166.4 167.9 168.5 169.9 170.7 171.8 172.8 173.7 174.8 175.6 176.8 177.5 178.7 179.3 180.5 181.1 182.3 182.9 184.0 184.7
# [93] 185.6 186.4 187.2 188.1 188.8 189.8 190.3 191.3 191.9 192.8 193.4 194.3 194.9 195.7 196.3 197.1 197.8 198.4 199.1 199.7 200.5 201.0 201.8
# [116] 202.3 203.0 203.5 204.3 204.8 205.4 206.0 206.6 207.1 207.7 208.3 208.8 209.4 209.9 210.5 210.9 211.5 211.9 212.5 213.0 213.5 213.9 214.5
# [139] 214.9 215.4 215.8 216.3 216.8 217.2 217.6 218.0 218.5 218.9 219.3 219.7So as the number of bets escalates, our expected payoff increases fairly quickly and we can get very close to the ceiling of $250 with canny betting.
Monte Carlo Tree Evaluation
If we do not have enough RAM to expand the full decision tree to its terminal nodes, there are many ways to approximate it. A simple one is to expand the tree as many levels far down as possible, and then if a terminal node is reached, do exact backwards induction, otherwise, at each pseudo-terminal node, approximate the value function somehow and then do backwards induction as usual. The deeper the depth, the closer the approximation becomes to the exact value, while still doing optimal planning within the horizon.
One way to approximate it would be to run a large number of simulations (perhaps 100) taking random actions until a terminal node is hit, and take the mean of the total values as the estimate. This would be a Monte Carlo tree evaluation. (This forms the conceptual basis of the famous MCTS/Monte Carlo tree search.) A random policy is handy because it can be used anywhere, but here we already know a good heuristic which does better than random: the KC. So we can use that instead. This gives us as much optimality as we can afford.
Setting up a simulation of the coin-flipping game which can be played with various strategies:
game <- function(strategy, wealth, betsLeft) {
if (betsLeft>0) {
bet <- strategy(wealth, betsLeft)
wealth <- wealth - bet
flip <- rbinom(1,1,p=0.6)
winnings <- 2*bet*flip
wealth <- min(wealth+winnings, 250)
return(game(strategy, wealth, betsLeft-1)) } else { return(wealth); } }
simulateGame <- function(s, w=25, b=300, iters=100) { mean(replicate(iters, game(s, w, b))) }
kelly <- function(w, b) { 0.20 * w }
smarterKelly <- function(w, b) { if(w==250) {0} else { (2*0.6-1) * w } }
random <- function(w, b) { sample(seq(0, w, by=0.1), 1) }
evaluate <- function(w,b) { simulateGame(smarterKelly, w, b) }
mevaluate <- memoise(evaluate)
mevaluate(25, 10)
# [1] 35.30544906
mevaluate(25, 100)
# [1] 159.385275
mevaluate(25, 300)
# [1] 231.4763619As expected the KC can do well and is just as fast to compute as a random action, so using it will give much better estimates of the value function for free.
With the Monte Carlo value function set up, the original value function can be slightly modified to include a maximum depth parameter and to evaluate using the MC value function instead once that maximum depth is hit:
f <- function(x, w, b, maxDepth) { 0.6*mV(min(w+x,250), b-1, maxDepth) + 0.4*mV(w-x, b-1, maxDepth)}
mf <- memoise(f)
V <- function(w,b, maxDepth) {
if (b<=(b-maxDepth)) { mevaluate(w,b) } else {
returns <- if (b>0 && w>0 && w<250) { sapply(seq(0, w, by=0.1), function(x) { mf(x,w,b, maxDepth) }) } else { w }
max(returns) }}
mV <- memoise(V)
mV(25, 300, 100); mV(25, 300, 50)Optimal next Action
One is also curious what the optimal strategy is, not just how much we can make with the optimal strategy given a particular starting point. As defined, I can’t see how to make mV return the optimal choices along the way, since it has to explore all choices bottom-up and can’t know what is optimal until it has popped all the way back to the root, and state can’t be threaded in because that defeats the memoization.
But then I remembered the point of computing value functions: given the (memoized) value function for each state, we can then plan by simply using V in a greedy planning algorithm by asking, at each step, for the value of each possible action (which is memoized, so it’s fast), and returning/choosing the action with the maximum value (which takes into account all the downstream effects, including our use of V at each future choice):
VPplan <- function(w, b) {
if (b==0) { return (0); } else {
returns <- sapply(seq(0, w), function(wp) { mf(wp, w, b); })
return (which.max(returns)-1); }
}
mVPplan <- memoise(VPplan)
## sanity checks:
mVPplan(250, 0)
# [1] 0
mVPplan(250, 1)
# [1] 0
mVPplan(25, 3)
# [1] 25It’s interesting that when b is very small, we want to bet everything on our first bet, because there’s not enough time to bother with recovering from losses; but as we increase b, the first bet will shrink & become more conservative:
firstAction <- sapply(1:150, function(b) { mVPplan(25, b) }); firstAction
# [1] 25 25 25 10 10 18 17 18 14 14 14 9 10 11 7 11 7 10 10 10 9 6 9 7 9 8 9 8 7 8 7 8 7 8 7 8 7 7 7 7 7 6 7 6 7 6 7
# [48] 6 6 6 6 6 6 6 6 6 6 6 6 5 6 5 6 5 6 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 4 5 4 5 4 5 4
# [95] 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 3
# [142] 4 3 4 3 4 3 3 3 3Optimizing
The foregoing is interesting but the R implementation is too slow to examine the case of most importance: b = 300. The issue is not so much the intrinsic difficulty of the problem—since the R implementation’s RAM usage is moderate even at b = 150, indicating that the boundary conditions do indeed tame the exponential growth & turn it into something more like quadratic growth—but the slowness of computing. Profiling suggests that most of the time is spent inside memoise:
# redefine to clear out any existing caching:
forget(mV)
Rprof(memory.profiling=TRUE, gc.profiling=TRUE, line.profiling=TRUE)
mV(w=25, b=9)
Rprof(NULL)
summaryRprof()Most of the time is spent in functions which appear nowhere in our R code, like lapply or deparse, which points to the behind-the-scenes memoise. Memoization should be fast because the decision tree can be represented as nothing but a multidimensional array in which one does lookups for each combination of w/b for a stored value V, and array lookups ought to be near-instantaneous. But apparently there is enough overhead to dominate our decision tree’s computation.
R does not provide native hash tables; what one can do is use R’s “environments” (which use hash tables under the hood), but are restricted to string keys (yes, really) as a poor man’s hash table by using digest to serialize & hash arbitrary R objects into string keys which can then be inserted into an ‘environment’. (I have since learned that there is a hashmap library which is a wrapper around a C++ hashmap implementation which should be usable: Nathan Russell’s hashmap.) The backwards induction remains the same and the hash-table can be updated incrementally without any problem (useful for switching to alternative methods like MCTS), so the rewrite is easy:
## crude hash table
library(digest)
## digest's default hash is MD5, which is unnecessarily slower, so use a faster hash:
d <- function (o) { digest(o, algo="xxhash32") }
lookup <- function(key) { get(d(key), tree) }
set <- function(key,value) { assign(envir=tree, d(key), value) }
isSet <- function(key) { exists(d(key), envir=tree) }
## example:
tree <- new.env(size=1000000, parent=emptyenv())
set(c(25,300), 50); lookup(c(25, 300))
# [1] 50
tree <- new.env(size=1000000, parent=emptyenv())
f <- function(x, w, b) {
0.6*V(min(w+x,250), b-1) + 0.4*V(w-x, b-1) }
V <- function(w, b) {
if (isSet(c(w,b))) { return(lookup(c(w,b))) } else {
returns <- if (b>0 && w>0 && w<250) { sapply(seq(0, w, by=0.1), function(x) { f(x,w,b) }) } else { return(w) }
set(c(w,b), max(returns))
return(lookup(c(w,b)))
}
}
V(25,5)While the overhead is not as bad as memoise, performance is still not great.
Python
Alternative naive & memorized implementations in Python.
Unmemoized version (a little different due to floating point):
import numpy as np # for enumerating bet amounts as a float range
def F(w, x, b):
return 0.6*V(min(w+x,250), b-1) + 0.4*V(w-x, b-1)
def V(w, b):
if b>0 and w>0 and w<250:
bets = np.arange(0, w, 0.1).tolist()
returns = [F(w,x,b) for x in bets]
else:
returns = [w]
return max(returns)
V(25,0)
V(25,0)
# 25
V(25,1)
# 29.98
V(25,2)
# 35.967999999999996
V(25,3)Python has hash-tables built in as dicts, so one can use those:
import numpy as np
def F(w, x, b, dt):
return 0.6*V(min(w+x,250), b-1, dt) + 0.4*V(w-x, b-1, dt)
def V(w, b, dt):
if b>0 and w>0 and w<250:
if (w,b) in dict:
return dict[(w,b)]
else:
bets = np.arange(0, w, 0.1).tolist()
returns = [F(w,x,b,dt) for x in bets]
else:
returns = [w]
best = max(returns)
dict[(w,b)] = best
return best
dict = {}
V(25, 0, dict)
# 25Haskell
Gurkenglas provides 2 inscrutably elegant & fast versions of the value function which works in GHCi:
(!!25) $ (!!300) $ (`iterate` [0..250]) $ \nextutilities -> (0:) $ (++[250]) $
tail $ init $ map maximum $ (zipWith . zipWith) (\up down -> 0.6 * up + 0.4 * down)
(tail $ tails nextutilities) (map reverse $ inits nextutilities)
-- 246.2080494949234
-- it :: (Enum a, Fractional a, Ord a) => a
-- (7.28 secs, 9,025,766,704 bytes)
:module + Control.Applicative
(!!25) $ (!!300) $ (`iterate` [0..250]) $ map maximum . liftA2 ((zipWith . zipWith)
(\up down -> 0.6 * up + 0.4 * down)) tails (map reverse . tail . inits)
- 246.2080494949234
-- it :: (Enum a, Ord a, Fractional a) => a
-- (8.35 secs, 6,904,047,568 bytes)Noting:
iterate f x = x : iterate f (f x)doesn’t need to think much about memoization. From right to left, the line reads “Given how much each money amount is worth when n games are left, you can zip together that list’s prefixes and suffixes to get a list of options for each money amount at (n+1) games left. Use the best for each, computing the new utility as a weighted average of the previous. At 0 and 250 we have no options, so we must manually prescribe utilities of 0 and 250. Inductively use this to compute utility at each time from knowing that at the end, money is worth itself. Look at the utilities at 300 games left. Look at the utility of $25.” Inductively generating that whole list prescribes laziness.
Since it’s Haskell, we can switch to compiled code and use fast arrays.
Implementations in Haskell have been written by Gurkenglas & nshepperd using array-memoize & Data.Vector (respectively):
import System.Environment (getArgs)
import Data.Function (iterate)
import Data.Function.ArrayMemoize (arrayMemo)
type Wealth = Int
type EV = Double
cap :: Wealth
cap = 250
value :: [Wealth -> EV]
value = iterate f fromIntegral where
f next = arrayMemo (0, cap) $ \x -> maximum [go w | w <- [0..min (cap - x) x]] where
go w = 0.6 * next (min cap (x+w)) + 0.4 * next (x-w)
main :: IO ()
main = do [x, b] <- map read <$> getArgs
print $ value !! b $ xThe second one is more low-level and uses laziness/“tying the knot” to implement the memoization; it is the fastest and is able to evaluate memo 25 300 in <12s: the value turns out to be $246. (If we assume that all games either end in $250 or $0, then this implies that 246⁄250 = 0.984 or >98.4% of decision-tree games hit the max, as compared to Haghani & Dewey’s estimate that ~95% of KC players would.) The memoization is done internally, so to access all values we do more logic within the lexical scope.
import System.Environment (getArgs)
import Data.Function (fix)
import Data.Function.Memoize (memoFix2)
import Data.Vector (Vector)
import qualified Data.Vector as V (generate, (!))
import qualified Data.MemoUgly as U (memo)
type Wealth = Int
type Bets = Int
type EV = Double
cap :: Wealth
cap = 250
value :: (Wealth -> Bets -> EV) -> Wealth -> Bets -> EV
value next 0 b = 0
value next w 0 = fromIntegral w
value next w b = maximum [go x | x <- [0..min (cap - w) w]]
where
go x = 0.6 * next (min cap (w+x)) (b-1) + 0.4 * next (w-x) (b-1)
-- There are 4 possible ways aside from 'array-memoize':
-- 1. Direct recursion.
direct :: Wealth -> Bets -> EV
direct = fix value
-- 2. Memoized recursion.
memo :: Wealth -> Bets -> EV
memo w b = cached_value w b
where
cached_value w b = table V.! b V.! w
table :: Vector (Vector EV)
table = V.generate (b + 1)
(\b -> V.generate (cap + 1)
(\w -> value cached_value w b))
-- 3. Memoized recursion using 'memoize' library; slower.
memo2 :: Wealth -> Bets -> EV
memo2 = memoFix2 value
-- 4. Memoize using 'uglymemo' library; also slower but global
memo3 :: Wealth -> Bets -> EV
memo3 = U.memo . direct
main :: IO ()
main = do [w, b] <- map read <$> getArgs
print (memo w b)We can obtain all values with a function like
memo3 :: [Wealth] -> [Bets] -> [EV]
memo3 ws bs = zipWith cached_value ws bs
where
cached_value w b = table V.! b V.! w
table :: Vector (Vector EV)
table = V.generate (maximum bs + 1)
(\b -> V.generate (cap + 1)
(\w -> value cached_value w b))and evaluate:
λ> map round (memo3 (repeat 25) [1..300])
-- [30,36,43,45,48,54,55,58,62,63,67,68,71,74,75,79,80,82,85,86,90,90,94,94,97,99,100,
-- 103,104,107,108,110,111,113,115,116,119,120,122,123,125,126,128,130,131,133,134,
-- 136,136,139,139,141,142,144,145,146,148,149,151,151,153,154,155,156,158,159,160,
-- 161,162,164,164,166,166,168,169,170,171,172,173,174,175,176,177,177,179,179,181,
-- 181,182,183,184,185,186,186,187,188,189,190,190,191,192,193,193,194,195,196,196,
-- 197,198,198,199,200,200,201,202,202,203,204,204,205,205,206,207,207,208,208,209,
-- 209,210,210,211,212,212,213,213,214,214,214,215,215,216,216,217,217,218,218,219,
-- 219,219,220,220,221,221,221,222,222,222,223,223,224,224,224,225,225,225,226,226,
-- 226,227,227,227,228,228,228,228,229,229,229,230,230,230,230,231,231,231,231,232,
-- 232,232,232,233,233,233,233,234,234,234,234,234,235,235,235,235,236,236,236,236,
-- 236,236,237,237,237,237,237,238,238,238,238,238,238,239,239,239,239,239,239,239,
-- 240,240,240,240,240,240,240,241,241,241,241,241,241,241,241,242,242,242,242,242,
-- 242,242,242,242,243,243,243,243,243,243,243,243,243,243,244,244,244,244,244,244,
-- 244,244,244,244,244,244,245,245,245,245,245,245,245,245,245,245,245,245,245,245,
-- 246,246,246,246,246,246,246,246,246,246,246,246,246]Exact Value Function
We could go even further with zip [1..3000] (memo3 (repeat 25) [1..3000]) (which takes ~118s). Interestingly, the value stops increasing around b = 2,150 (V = 249.99009946798637) and simply repeats from there; it does not actually reach 250.
This is probably because with a stake of $25 it is possible (albeit extremely unlikely) to go bankrupt (gambler’s ruin) even betting the minimal fixed amount of $1. (The original Haskell code is modeled after the R, which discretized this way for tractability; however, since the Haskell code is so fast, this is now unnecessary.) If this is the case, then being able to bet smaller amounts should allow expected value to converge to $250 as exactly as can be computed, because the probability of going bankrupt after 2500 bets of $0.01 each is effectively zero—as far as R and Haskell will compute without special measures, 0.42500 = 0. We can go back and model the problem exactly as it was in the paper by simply multiply everything by 100 & interpreting in pennies:
cap = 25000 -- 250*100
-- ...
λ> zip [1..3000] (memo3 (repeat (25*100)) [1..3000])
[(1,3000.0),(2,3600.0),(3,4320.0),(4,4536.000000000002),(5,4795.200000000003),
(6,5365.440000000002),(7,5458.752000000004),(8,5757.350400000005),(9,6182.853120000005),(10,6260.488704000007),
(11,6676.137676800007),(12,6822.331453440009),(13,7060.11133132801),(14,7413.298296422411),(15,7499.673019514893),
(16,7913.219095166989),(17,7974.777338678492),(18,8250.07680018581),(19,8471.445742115113),(20,8625.387566014524),
(21,8979.7747405993),(22,9028.029532170909),(23,9384.523360172316),(24,9449.401095461177),(25,9699.670042282964),
(26,9882.821122181414),(27,10038.471393315525),(28,10323.078038637072),(29,10394.862038743217),(30,10760.507349554608),
(31,10763.85850433795),(32,11040.414570571116),(33,11141.364854687306),(34,11337.607662912955),(35,11524.013477359924),
(36,11648.117264906417),(37,11909.035644688667),(38,11968.56153182668),(39,12294.156320547045),(40,12296.062638839443),
(41,12554.172237535688),(42,12628.174503649356),(43,12820.701630209007),(44,12962.820770637838),(45,13095.979243218648),
(46,13298.241837094192),(47,13377.799870378874),(48,13632.949691989288),(49,13664.245374230446),(50,13935.591599024072),
(51,13953.650302164471),(52,14168.318904539414),(53,14244.57145315508),(54,14407.574739209653),(55,14535.761032800987),
(56,14651.76990919319),(57,14826.143029982914),(58,14899.500923102909),(59,15114.7924517843),(60,15149.530755496799),
(61,15399.983335449066),(62,15400.771450460255),(63,15604.908915203496),(64,15652.268440952908),(65,15813.476931576255),
(66,15903.186446379666),(67,16025.159151461572),(68,16152.79680966944),(69,16238.976728976708),(70,16400.466139297678),
(71,16454.05880056233),(72,16645.646128447275),(73,16669.63235112316),(74,16880.735724497223),(75,16885.012958972715),
(76,17058.916142797243),(77,17099.596358241968),(78,17239.339510457277),(79,17312.850756552616),(80,17421.275332110683),
(81,17524.309847338853),(82,17604.068867939182),(83,17733.56645905442),(84,17787.13463287746),(85,17940.266786525535),
(86,17969.95038247786),(87,18144.105153480315),(88,18152.051576292564),(89,18315.336828409476),(90,18333.026286703964),
(91,18467.997509430665),(92,18512.510521892633),(93,18621.43451689773),(94,18690.183932686265),(95,18775.180977557586),
(96,18865.765874427907),(97,18928.817685066606),(98,19039.0117965317),(99,19081.969208988696),(100,19209.70993405155),
(101,19234.300290845116),(102,19377.678277281033),(103,19385.51250899971),(104,19524.210291319585),(105,19535.341194745335),
(106,19651.63659936918),(107,19683.55258264968),(108,19779.19175398216),(109,19829.94117896368),(110,19906.559349360658),
(111,19974.327332744302),(112,20033.4549154762),(113,20116.554995203987),(114,20159.623419373274),(115,20256.489653646044),
(116,20284.836941737507),(117,20394.01642719967),(118,20408.892517902153),(119,20529.038285622184),(120,20531.61013289084),
(121,20639.865300258658),(122,20652.830860566657),(123,20744.14900653099),(124,20772.415137446053),(125,20848.093322557295),
(126,20890.24116222975),(127,20951.49506668366),(128,21006.203412595118),(129,21054.171837601196),(130,21120.21127127963),
(131,21155.960430614512),(132,21232.187753960352),(133,21256.71536121999),(134,21342.06833189189),(135,21356.30748944987),
(136,21449.7998427048),(137,21454.622738748447),(138,21545.893033861896),(139,21551.56090345761),(140,21629.60553083633),
(141,21647.034539300425),(142,21712.842497605183),(143,21740.96793155338),(144,21795.467123757197),(145,21833.2961358927),
(146,21877.356736609778),(147,21923.964087187007),(148,21958.401746908596),(149,22012.92577178374),(150,22038.504663866137),
(151,22100.143459100647),(152,22117.579175397976),(153,22185.586988586107),(154,22195.549289624447),(155,22269.23310835155),
(156,22272.348533907876),(157,22343.200726693787),(158,22347.9192078922),(159,22408.92268721723),(160,22422.211687202966),
(161,22474.09110290414),(162,22495.183774650206),(163,22538.619509420547),(164,22566.800095953415),(165,22602.430698828903),
(166,22637.031537177958),(167,22665.456036220217),(168,22705.854721234122),(169,22727.634820414445),(170,22773.2515209447),
(171,22788.913686133077),(172,22839.208606334214),(173,22849.246045182404),(174,22903.71702393249),(175,22908.591564315902),
(176,22966.44249475668),(177,22966.915677569094),(178,23017.91541566918),(179,23024.18913098028),(180,23068.1913376925),
(181,23080.387557725626),(182,23117.90218718125),(183,23135.491081806776),(184,23166.99717629234),(185,23189.48394853381),
(186,23215.431334191013),(187,23242.35418014611),(188,23263.165077204263),(189,23294.093255008785),(190,23310.163806371635),
(191,23344.695808912184),(192,23356.397530793947),(193,23394.159357087876),(194,23401.840515265318),(195,23442.484035635396),
(196,23446.47095075504),(197,23489.640293583914),(198,23490.270646383346),(199,23529.46834312825),(200,23533.224741609163),
(201,23567.312697440484),(202,23575.321437418483),(203,23604.666095269786),(204,23616.551745369172),(205,23641.497567737664),
(206,23656.90925341186),(207,23677.779921209272),(208,23696.38990746728),(209,23713.489458166325),(210,23734.991807798215),
(211,23748.60571568506),(212,23772.71501926872),(213,23783.111220502426),(214,23809.56139463541),(215,23816.991259707916),
(216,23845.534410064567),(217,23850.233666149958),(218,23880.639012115425),(219,23882.82861769509),(220,23914.391375329913),
(221,23914.76844952492),(222,23942.714790600083),(223,23946.0474787004),(224,23970.438187949254),(225,23976.66184026535),
(226,23997.74934793851),(227,24006.60933420138),(228,24024.631040582935),(229,24035.889282584474),(230,24051.068374275732),
(231,24064.50239633),(232,24077.048621078735),(233,24092.450650947027),(234,24102.561052984205),(235,24119.737170755707),
(236,24127.59678851838),(237,24146.366121052237),(238,24152.148649090945),(239,24172.342607735227),(240,24176.211024526496),
(241,24197.672583935127),(242,24199.779747244538),(243,24222.35471729034),(244,24222.851974583486),(245,24243.93438158678),
(246,24245.42607879143),(247,24263.972996501543),(248,24267.50154423283),(249,24283.6900658947),(250,24289.078871384656),
(251,24303.07565677869),(252,24310.159487219513),(253,24322.121319078917),(254,24330.74566159496),(255,24340.819980440137),
(256,24350.840429290023),(257,24359.165841053073),(258,24370.447517349417),(259,24377.154275094566),(260,24389.571277415347),
(261,24394.781738403053),(262,24408.216622744527),(263,24412.045682031203),(264,24426.388969625325),(265,24428.94447133704),
(266,24444.09418292577),(267,24445.477310292874),(268,24461.32346887292),(269,24461.644170708976),(270,24476.42136455785),
(271,24477.445726085083),(272,24490.501181704694),(273,24492.883289818776),(274,24504.335944986862),(275,24507.958757514363),
(276,24517.920620087607),(277,24522.6745531501),(278,24531.251041416166),(279,24537.03357887482),(280,24544.32387659046),
(281,24551.039168217816),(282,24557.136561611253),(283,24564.69504250772),(284,24569.687240115927),(285,24578.005270307505),
(286,24581.974706479406),(287,24590.97422968356),(288,24593.998352542163),(289,24603.606573136858),(290,24605.75811775705),
(291,24615.907195034095),(292,24617.254442557904),(293,24627.881197714756),(294,24628.488224763427),(295,24639.274079225856),
(296,24639.46077884001),(297,24649.128469095107),(298,24650.173797856685),(299,24658.72751316172),(300,24660.629317974468)
...
(1884,24999.999999999614),(1885,24999.99999999963),(1886,24999.999999999643),(1887,24999.999999999658),(1888,24999.99999999967),
(1889,24999.99999999968),(1890,24999.999999999694),(1891,24999.9999999997),(1892,24999.999999999716),(1893,24999.999999999727),
(1894,24999.999999999738),(1895,24999.99999999975),(1896,24999.99999999976),(1897,24999.999999999767),(1898,24999.99999999978),
(1899,24999.99999999979),(1900,24999.9999999998),(1901,24999.99999999981),(1902,24999.999999999818),(1903,24999.999999999825),
(1904,24999.999999999833),(1905,24999.999999999844),(1906,24999.999999999854),(1907,24999.99999999986),(1908,24999.99999999987),
(1909,24999.999999999876),(1910,24999.999999999884),(1911,24999.99999999989),(1912,24999.999999999898),(1913,24999.999999999905),
(1914,24999.999999999913),(1915,24999.99999999992),(1916,24999.999999999924),(1917,24999.999999999927),(1918,24999.999999999935),
(1919,24999.99999999994),(1920,24999.99999999995),(1921,24999.99999999995),(1922,24999.999999999956),(1923,24999.999999999964),
(1924,24999.999999999967),(1925,24999.99999999997),(1926,24999.999999999978),(1927,24999.999999999978),(1928,24999.999999999985),
(1929,24999.99999999999),(1930,24999.999999999993),(1931,24999.999999999993),(1932,25000.0),(1933,25000.0),
(1934,25000.0),(1935,25000.0),(1936,25000.0),(1937,25000.0),(1938,25000.0),
(1939,25000.0),(1940,25000.0),(1941,25000.0),(1942,25000.0),(1943,25000.0),
(1944,25000.0),(1945,25000.0),(1946,25000.0),(1947,25000.0),(1948,25000.0),
(1949,25000) ... ]With the exact penny version, the value of b = 300 is now $246.6062932 (taking ~3746s compiled), so the approximation costs an expected value of only $0.61. The full run reveals that convergence happens at b = 193294ya (which can be computed in ~48503s compiled), past which there is no need to compute further.
C/C++
FeepingCreature provides a vectorized C implementation of the exact penny game that runs in a few minutes (benefiting ~13% from profile-guided optimization when compiled with GCC).
He also notes that “top-down” memoization/dynamic programming is overkill for this problem: because almost all states ultimately get evaluated, the dynamic programming doesn’t avoid evaluating many states. Since each state depends on an immediate successor and forms a clean tree, it is possible to calculate the tree much more directly “bottom-up” by evaluating all the terminal nodes b = 0, looping over the previous nodes b+1, then throwing away the no longer necessary b, and evaluating b+2, and so on; only two layers of the tree need to be stored at any time, which can potentially fit into on-processor cache & have better cache locality. Another advantage of this representation is parallelism, as each node in the upper layer can be evaluated independently.
An implementation using OpenMP for threading can solve b = 300 in ~8s:
#include <stdlib.h>
#include <stdio.h>
#include <stdbool.h>
#include <math.h>
#define ROUND_LIMIT 300
#define MONEY_LIMIT 25000
#define MONEY_START 2500
#define MONEY_FACTOR 100.0f
// #define DATATYPE float
// #define F(X) X ## f
#define DATATYPE double
#define F(X) X
#define THREADS 8
// MEMOIZED METHOD
typedef struct {
bool known;
DATATYPE ev;
} CacheEntry;
static DATATYPE decide(CacheEntry * const table, int money, int round) {
if (round < 0) return money;
if (money == 0 || money == MONEY_LIMIT) return money;
int index = round * (MONEY_LIMIT + 1) + money;
// int index = money * ROUND_LIMIT + round;
if (table[index].known) return table[index].ev;
DATATYPE best_bet_score = -1;
for (int bet = 0; bet <= money; bet++) {
DATATYPE winres = decide(table, (money + bet > MONEY_LIMIT) ? MONEY_LIMIT : (money + bet), round - 1);
DATATYPE loseres = decide(table, money - bet, round - 1);
DATATYPE combined = F(0.6) * winres + F(0.4) * loseres;
best_bet_score = F(fmax)(best_bet_score, combined);
}
table[index] = (CacheEntry) { true, best_bet_score };
return best_bet_score;
}
void method1() {
CacheEntry *table = calloc(sizeof(CacheEntry), ROUND_LIMIT * (MONEY_LIMIT + 1));
printf("running.\n");
int best_bet = 0;
DATATYPE best_bet_score = -1;
for (int bet = 0; bet <= MONEY_START; bet++) {
DATATYPE winres = decide(table, MONEY_START + bet, ROUND_LIMIT - 1);
DATATYPE loseres = decide(table, MONEY_START - bet, ROUND_LIMIT - 1);
DATATYPE combined = F(0.6) * winres + F(0.4) * loseres;
if (combined > best_bet_score) {
best_bet = bet;
best_bet_score = combined;
}
}
printf("first round: bet %f for expected total reward of %f\n", best_bet / MONEY_FACTOR, best_bet_score / MONEY_FACTOR);
int count_known = 0;
for (int i = 0; i < ROUND_LIMIT * (MONEY_LIMIT + 1); i++) {
if (table[i].known) count_known ++;
}
printf("known: %i of %i\n", count_known, ROUND_LIMIT * (MONEY_LIMIT + 1));
}
// BOTTOM-UP METHOD
// given pass n in "from", compute pass n-1 in "to"
static void propagate(DATATYPE *from, DATATYPE *to) {
// for each money state...
#pragma omp parallel for num_threads(THREADS)
for (int a = 0; a < THREADS; a++) {
// distribute workload so that inner loop passes are approximately equal
// f(x) = 2x F(x) = x^2 = a/THREADS x = sqrt(a / THREADS)
int low = (int) (MONEY_LIMIT * sqrtf((float)a / THREADS));
int high = (int) (MONEY_LIMIT * sqrtf((a + 1.0f) / THREADS));
if (a == THREADS - 1) high = MONEY_LIMIT + 1; // precise upper border
for (int m = low; m < high; m++) {
DATATYPE max_score = 0.0;
// determine the bet that maximizes our expected earnings
// to enable vectorization we break the loop into two so that each half only gets one branch of the conditional
// DATATYPE winval = from[(m + b > MONEY_LIMIT) ? MONEY_LIMIT : (m + b)];
int high_inner = (m + m > MONEY_LIMIT) ? (MONEY_LIMIT - m) : m;
for (int b = 0; b <= high_inner; b++) {
DATATYPE winval = from[m + b];
DATATYPE loseval = from[m - b];
DATATYPE combined = F(0.6) * winval + F(0.4) * loseval;
max_score = F(fmax)(max_score, combined);
}
for (int b = high_inner + 1; b <= m; b++) {
DATATYPE winval = from[MONEY_LIMIT];
DATATYPE loseval = from[m - b];
DATATYPE combined = F(0.6) * winval + F(0.4) * loseval;
max_score = F(fmax)(max_score, combined);
}
to[m] = max_score;
}
}
}
void method2() {
DATATYPE *buf = malloc(sizeof(DATATYPE) * (MONEY_LIMIT + 1));
DATATYPE *buf_to = malloc(sizeof(DATATYPE) * (MONEY_LIMIT + 1));
// set up base case: making no bet, we have money of i
for (int i = 0; i <= MONEY_LIMIT; i++) buf[i] = i;
for (int i = ROUND_LIMIT - 1; i >= 0; i--) {
propagate(buf, buf_to);
DATATYPE *temp = buf;
buf = buf_to;
buf_to = temp;
}
int best_bet = 0;
DATATYPE best_bet_score = -1;
for (int b = 0; b <= MONEY_START; b++) {
DATATYPE winval = buf[MONEY_START + b];
DATATYPE loseval = buf[MONEY_START - b];
DATATYPE combined = 0.6 * winval + 0.4 * loseval;
if (combined > best_bet_score) {
best_bet_score = combined;
best_bet = b;
}
}
printf("first round: bet %f for expected total reward of %f\n", best_bet / MONEY_FACTOR, best_bet_score / MONEY_FACTOR);
}
int main() {
method2();
return 0;
}Some quick benchmarking on my 2016 Lenovo ThinkPad P70 laptop with 4 physical cores & 8 virtual cores (Intel Xeon E3-1505M v5 Processor 8MB Cache / up to 3.70GHz) shows a roughly linear speedup 1 → 3 threads and then small gains thereafter to a minimum of 7.2s with 8 threads:
for C in `ls coingame-*.c`; do
gcc -Wall -Ofast -fwhole-program -march=native -fopenmp $C -o coingame -lm &&
echo "$C" &&
(for i in {1..10}; do
/usr/bin/time -f '%e' ./coingame; done
);
doneFor levels of parallelism on my laptop from 1–8 threads, the average times are: 28.98s/15.44s/10.70s/9.22s/9.10s/8.4s/7.66s/7.20s.
Caio Oliveira provides a parallel C++ implementation using std::async; compiled with the same optimizations on (g++ -Ofast -fwhole-program -march=native -pthread --std=c++11 kc.cpp -o kc), it runs in ~1m16s:
#include <iostream>
#include <vector>
#include <map>
#include <set>
#include <bitset>
#include <list>
#include <stack>
#include <queue>
#include <deque>
#include <string>
#include <sstream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <future>
#include <ctime>
using namespace std;
const int MAX_ROUND = 300;
const int MAX_WEALTH = 25000;
const int BETS_DELTA = 1;
double memo[MAX_WEALTH + 1][2];
inline double vWin(int wealth, int bet, int roundIdx) {
if(wealth + bet < MAX_WEALTH) {
return memo[wealth + bet][!roundIdx];
}
else {
return MAX_WEALTH;
}
}
inline double vLose(int wealth, int bet, int roundIdx) {
if (wealth - bet == 0) {
return 0;
}
else {
return memo[wealth - bet][!roundIdx];
}
}
inline double v(int wealth, int bet, int roundIdx) {
return .6 * vWin(wealth, bet, roundIdx) + .4 * vLose(wealth, bet, roundIdx);
}
template<typename RAIter>
void calc_round(RAIter beg, RAIter end, int roundIdx){
int len = distance(beg, end);
if(len < 1000) {
for(RAIter p = beg; p != end; ++p) {
int wealth = distance(memo, p);
(*p)[roundIdx] = v(wealth, wealth, roundIdx);
for (int bet = 0; bet < wealth; bet += BETS_DELTA) {
memo[wealth][roundIdx] = max(memo[wealth][roundIdx], v(wealth, bet, roundIdx));
}
}
}
else {
RAIter mid = beg + len/2;
future<void> handle = async(launch::async, calc_round<RAIter>, mid, end, roundIdx);
calc_round(beg, mid, roundIdx);
}
}
double calc_table() {
bool roundIdx = 0;
for(int i = 0; i <= MAX_WEALTH; ++i) {
memo[i][!roundIdx] = i;
}
for(int round = MAX_ROUND - 1; round >= 0; --round) {
calc_round(memo, memo + MAX_WEALTH, roundIdx);
roundIdx ^= 1;
}
return memo[2500][!roundIdx] / 100.;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
clock_t begin = clock();
double res = calc_table();
clock_t end = clock();
cout << "result: " << res << "(elapsed: " << (double(end - begin) / CLOCKS_PER_SEC) << ")" << endl;
}Given the locality of the access patterns, I have to wonder how well a GPU implementation might perform? It doesn’t seem amenable to being expressed as a large matrix multiplication, but each GPU core could be responsible for evaluating a terminal node and do nearby lookups from there. (And the use in finance of GPUs to compute the lattice model/binomial options pricing model/trinomial tree model, which are similar, suggests it should be possible.)
Exact Formula
Arthur Breitman notes that “you can compute U(w,b) in 𝒪(b) if you allow bets to be any fraction of w. It’s piecewise linear, the cutoff points and slopes follow a very predictable pattern”1 and provides a formula for calculating the value function without constructing a decision tree:
A short version in R:
V <- function(w, b, m=250) {
b <- round(b) # rounds left must be integer
j <- qbinom(w/m, b, 0.5)
1.2^b * 1.5^-j * (w + (m/2 * sum(1.5^(j:0) * pbinom(0:j-1,b,1/2)))) }(This is sufficiently fast for all values tested that it is not worth memoizing using the relatively slow memoise.)
Re-implementing in Python is a little tricky because NumPy/SciPy use different names and Python doesn’t support R’s range notation, but the following seems like it works; and then with a value function, we can implement a planner to choose optimal betting amounts, memoize it with repoze.lru for time-savings over multiple games, and then it is simple to set up a Gym environment and start playing the Kelly coin-flip game optimally (and indeed usually reaching the $250 limit):
from scipy.stats import binom
import numpy as np
from repoze.lru import lru_cache
def V(w, b, m=250):
if w>=250:
return 250
if w<=0:
return 0
if b==0:
return w
else:
try:
j = binom.ppf(float(w)/float(m), b, 0.5)
return 1.2**b * 1.5**-j * (w + m/2 *
sum(np.multiply(binom.cdf(map(lambda(x2):x2-1, range(0,int(j+1))),b,0.5),
map(lambda(x): 1.5**x, list(reversed(range(0, int(j+1))))))))
except ValueError:
print "Error:", (w,b,m)
@lru_cache(None)
def VPplan(w, b):
# optimization: short-circuit
if w<=0 or w>=250:
return 0
else:
if b==0:
return w
else:
possibleBets = map(lambda(pb): float(pb)/100.0, range(0*100,int((w*100)+1),1))
returns = map(lambda(pb): 0.6*V(w+pb, b-1) + 0.4*V(w-pb,b-1), possibleBets)
return float(returns.index(max(returns)))/100.0import gym
env = gym.make('KellyCoinflip-v0')
## play 500 games and calculate mean reward:
rewards = []
for n in range(0,500):
done = False
reward = 0
while not done:
w = env._get_obs()[0][0]
b = env._get_obs()[1]
bet = VPplan(w, b)
results = env._step(bet*100)
print n, w, b, bet, "results:", results
reward = reward+results[1]
done = results[2]
rewards.append(reward)
env._reset()
print sum(rewards)/len(rewards)
# 247.525564356Graphing the Value Function
What does the range of possible bets in each state look like? Does it look bitonic and like an inverted V one could do binary search on? We can sample some random states, compute all the possible bets, and plot them by index to see if the payoffs form curves:
# return all actions' values instead of the max action:
VPplans <- function(w, b) {
if (b==0) { return (0); } else {
returns <- sapply(seq(0, w), function(wp) { mf(wp, w, b); })
return(returns); } }
plans <- data.frame()
n <- 47
for (i in 1:n) {
# omit the uninteresting cases of w=0/250 and b=0/300:
w <- round(runif(n=1, 0+1, 250-1))
b <- round(runif(n=1, 0+1, 300-1))
plan <- VPplans(w,b)
plans <- rbind(plans, data.frame(W=as.factor(w), B=as.factor(b), Bet=1:(length(plan)), Value=plan))
}
library(ggplot2)
p <- qplot(x=Bet, y=Value, data=plans)
p + facet_wrap(~W) + geom_line(aes(x=Bet, y=Value, color=W), size = 1) + theme(legend.position = "none")For the most part they do generally follow a quadratic or inverted-V like shape, with the exception of several which wiggle up and down while following the overall curve (numeric or approximation error?).

47 randomly-sampled states with all legal bets’ exact value plotted, showing generally smooth curves
With an exact value function, we can also visualize it to get an idea of how the wealth/rounds interact and how difficult it would be to approximate it. We can generate many iterates, interpolate, and graph:
n <- 50000
w <- runif(n, min=0, max=250)
b <- sample(0:250, n, replace=TRUE)
v <- unlist(Map(V, w, b))
df <- data.frame(Wealth=w, Rounds=b, Value=v)
library(akima)
library(plot3D)
dfM <- interp(df$Wealth, df$Rounds, df$Value, duplicate="strip")
par(mfrow=c(1,2), mar=0)
persp(dfM$x, dfM$y, dfM$z, xlab="Wealth", ylab="Rounds left", zlab="Value", ticktype="detailed")
scatter3D(df$Wealth, df$Rounds, df$Value, theta=-25, xlab="Wealth", ylab="Rounds left", zlab="Value", ticktype="detailed")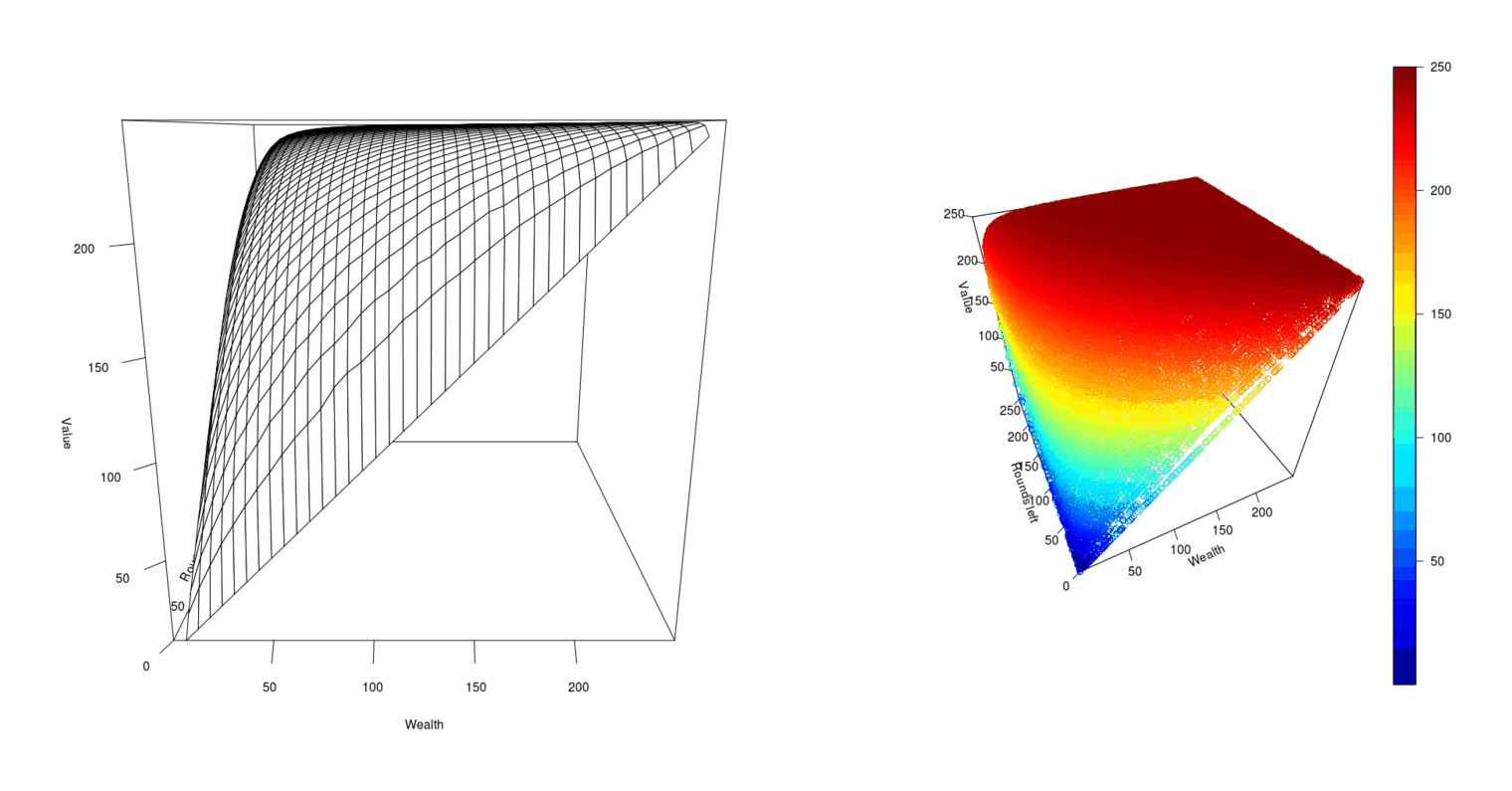
3D plots of the value function varying with wealth available to bet & rounds left to bet in in order to reach the $250 maximum payout
Approximating the Exact Value Function
The value function winds up looking simple, a smooth landscape tucked down at the edges, which is perhaps not too surprising, as the optimal betting patterns tend to be small amounts except when there are very few rounds left (and one should bet most or all of one’s wealth) or one is nearing the maximum wealth cap (and should very gradually glide in).
A value function (or the policy function) computed by decision trees is bulky and hard to carry around, weighing perhaps gigabytes in size. Looking at this value function, it’s clear that we can do model distillation and easily approximate it by another algorithm like random forests or neural networks. (Usually, a NN has a hard time learning a value function because it’s a reinforcement learning problem where it’s unclear how actions are linked to rewards, but in this case, since we can already calculate it, it becomes the far easier setting of supervised learning in mapping a state to a value/policy.)
A random forest works fine, getting 0.4 RMSE:
library(randomForest)
r <- randomForest(Value ~ Wealth + Rounds, ntree=1000, data=df); r
# ...
# Mean of squared residuals: 1.175970325
# % Var explained: 99.94
sqrt((predict(r) - df$Value)^2)
# [1] 0.407913389It can also be approximated with NN. For example, in R one can use MXNet and a 1×30 or 2×152 ReLu feedforward NN will solve it to <4 RMSE:
## very slow
library(neuralnet)
n <- neuralnet(Value ~ Wealth + Rounds, data=df, hidden=c(20,20))
# prediction(n)
## GPU-accelerated:
library(mxnet)
mx.set.seed(0)
## 2×30 ReLu FC NN for linear regression with RMSE loss:
data <- mx.symbol.Variable("data")
perLayerNN <- 30
fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=perLayerNN)
act1 <- mx.symbol.Activation(fc1, name="relu1", act_type="relu")
fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=perLayerNN)
act2 <- mx.symbol.Activation(fc2, name="relu2", act_type="relu")
fc3 <- mx.symbol.FullyConnected(act2, name="fc2", num_hidden=perLayerNN)
act3 <- mx.symbol.Activation(fc3, name="relu2", act_type="relu")
finalFc <- mx.symbol.FullyConnected(act3, num_hidden=1)
lro <- mx.symbol.LinearRegressionOutput(finalFc)
model <- mx.model.FeedForward.create(lro, X=as.matrix(subset(df,select=c("Wealth","Rounds"))), y=df$Value,
ctx=mx.gpu(), num.round=50000,
learning.rate=5e-6, eval.metric=mx.metric.rmse, array.layout="rowmajor")Some experimenting with fitting polynomial regressions did not give any decent fits for less than quintic, but probably some combination of logs and polynomials could compactly encode the value function.
Simulation Performance
The implementations here could be wrong, or decision trees not actually optimal like claimed. We can test it by directly comparing the performance in a simulation of the coin-flipping game, comparing the performance of mVPplan vs the 20% Kelly criterion and a simple bet-everything strategy:
library(memoise)
f <- function(x, w, b) { 0.6*V(min(w+x,250), b-1) + 0.4*V(w-x, b-1)}
mf <- memoise(f)
V <- function(w, b, m=250) { j <- qbinom(w/m,b,1/2);
1.2^b * 1.5^-j * (w+m/2 * sum(1.5^(j:0) * pbinom(0:j-1,b,1/2))) }
VPplan <- function(w, b) {
if (b==0) { return (0); } else {
returns <- sapply(seq(0, w), function(wp) { mf(wp, w, b); })
return (which.max(returns)-1); }
}
mVPplan <- memoise(VPplan)
game <- function(strategy, wealth, betsLeft) {
if (betsLeft>0) {
bet <- strategy(wealth, betsLeft)
wealth <- wealth - bet
flip <- rbinom(1,1,p=0.6)
winnings <- 2*bet*flip
wealth <- min(wealth+winnings, 250)
return(game(strategy, wealth, betsLeft-1)) } else { return(wealth); } }
simulateGame <- function(s, w=25, b=300, iters=5000) { mean(replicate(iters, game(s, w, b))) }
## Various strategies (the decision tree strategy is already defined as 'mVPplan'):
kelly <- function(w, b) { 0.20 * w }
smarterKelly <- function(w, b) { if(w==250) {0} else { 0.2 * w } }
maximizer <- function(w, b) { w; }
smarterMaximizer <- function(w, b) { if(w>=250) { 0 } else {w}; }
## examining a sample of how wealth evolves over the course of a sample of b=300 games:
library(parallel)
library(plyr)
i <- 56
games <- ldply(mclapply(1:i, function(ith) {
b <- 300
wealth <- 25
wealths <- numeric(b)
while (b>0) {
bet <- mVPplan(wealth, b)
wealth <- wealth-bet
flip <- rbinom(1,1,p=0.6)
winnings <- 2*bet*flip
wealth <- min(wealth+winnings, 250)
wealths[b] <- wealth
b <- b-1
}
return(data.frame(Game=ith, Bets=300:1, Wealth=wealths)) }
))
library(ggplot2)
p <- qplot(x=Bets, y=Wealth, data=games)
p + facet_wrap(~Game) + geom_line(aes(x=Bets, y=Wealth), size = 1) + theme(legend.position = "none")Simulating 56 games, we can see how while the optimal strategy looks fairly risky, it usually wins in the end:
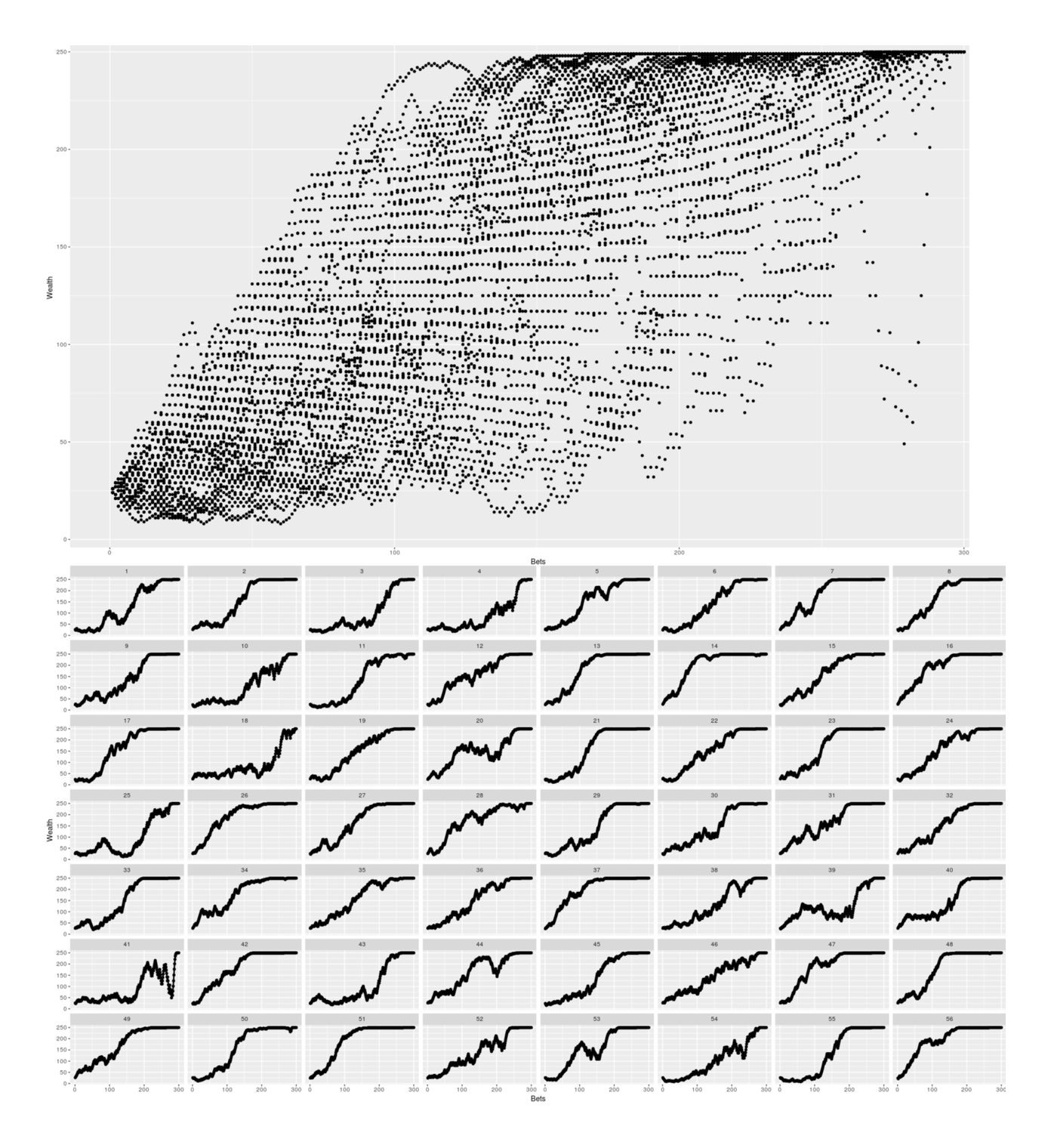
Simulation of winnings over a sample of b = 300 games while using the optimal strategy.
We can also examine how the strategy does for all the other possible horizons and compare with the Kelly.
## Comparing performance in the finite horizon setting up to b=300:
bs <- 1:300
ldply(mclapply(bs, function(bets) {
ky <- round(simulateGame(smarterKelly, b=bets), digits=1)
dt <- round(simulateGame(mVPplan, b=bets), digits=1)
gain <- dt-ky;
print(paste(bets, round(V(25, bets), digits=2), dt, ky, gain)) }
))Simulating 5,000 games for each b:
Total bets |
Value function |
Decision tree performance |
Kelly performance |
Difference |
|---|---|---|---|---|
1 |
30 |
30.1 |
26 |
4.1 |
2 |
36 |
35.5 |
27 |
8.5 |
3 |
43.2 |
42.4 |
28.2 |
14.2 |
4 |
45.36 |
46 |
29.3 |
16.7 |
5 |
47.95 |
49.3 |
30.5 |
18.8 |
6 |
53.65 |
52.5 |
31.5 |
21 |
7 |
54.59 |
51.4 |
32.7 |
18.7 |
8 |
57.57 |
56.1 |
34.1 |
22 |
9 |
61.83 |
61.4 |
35.6 |
25.8 |
10 |
62.6 |
63 |
36.8 |
26.2 |
11 |
66.76 |
68.6 |
38.3 |
30.3 |
12 |
68.22 |
66.9 |
40.2 |
26.7 |
13 |
70.6 |
70.7 |
41.8 |
28.9 |
14 |
74.13 |
71.2 |
43.2 |
28 |
15 |
75 |
73.8 |
44.9 |
28.9 |
16 |
79.13 |
79.7 |
46.8 |
32.9 |
17 |
79.75 |
79.1 |
47.8 |
31.3 |
18 |
82.5 |
84.1 |
50.1 |
34 |
19 |
84.71 |
83.7 |
52.7 |
31 |
20 |
86.25 |
85.6 |
54.2 |
31.4 |
21 |
89.8 |
88.6 |
56.4 |
32.2 |
22 |
90.28 |
90.2 |
56.5 |
33.7 |
23 |
93.85 |
94.8 |
58.7 |
36.1 |
24 |
94.49 |
93.7 |
60.7 |
33 |
25 |
97 |
95 |
62.2 |
32.8 |
26 |
98.83 |
97.1 |
65.2 |
31.9 |
27 |
100.38 |
98.7 |
68.1 |
30.6 |
28 |
103.23 |
102.1 |
69.4 |
32.7 |
29 |
103.95 |
102.5 |
73.4 |
29.1 |
30 |
107.61 |
107.7 |
73.7 |
34 |
31 |
107.64 |
107.3 |
74.7 |
32.6 |
32 |
110.4 |
106.7 |
76.1 |
30.6 |
33 |
111.41 |
107.9 |
79.2 |
28.7 |
34 |
113.38 |
115.1 |
80.6 |
34.5 |
35 |
115.24 |
115.4 |
82.2 |
33.2 |
36 |
116.48 |
116.1 |
84.2 |
31.9 |
37 |
119.09 |
118.5 |
87.1 |
31.4 |
38 |
119.69 |
119.9 |
86 |
33.9 |
39 |
122.94 |
125.4 |
89.6 |
35.8 |
40 |
122.96 |
119.7 |
92 |
27.7 |
41 |
125.54 |
124.2 |
95.2 |
29 |
42 |
126.28 |
124.4 |
96.9 |
27.5 |
43 |
128.21 |
128.5 |
97.1 |
31.4 |
44 |
129.63 |
130.5 |
100.3 |
30.2 |
45 |
130.96 |
130.1 |
100 |
30.1 |
46 |
132.98 |
131.9 |
100.9 |
31 |
47 |
133.78 |
132.4 |
104.2 |
28.2 |
48 |
136.33 |
134.2 |
104.5 |
29.7 |
49 |
136.64 |
133.6 |
107.7 |
25.9 |
50 |
139.36 |
141.2 |
110.1 |
31.1 |
51 |
139.54 |
139.4 |
113.6 |
25.8 |
52 |
141.68 |
140 |
113 |
27 |
53 |
142.45 |
140.7 |
113.5 |
27.2 |
54 |
144.08 |
141.8 |
115.5 |
26.3 |
55 |
145.36 |
145 |
116.3 |
28.7 |
56 |
146.52 |
150.2 |
119.7 |
30.5 |
57 |
148.26 |
146.4 |
119.7 |
26.7 |
58 |
149 |
143.9 |
120.6 |
23.3 |
59 |
151.15 |
151.8 |
124.2 |
27.6 |
60 |
151.5 |
148.5 |
124.4 |
24.1 |
61 |
154.01 |
151.9 |
125.5 |
26.4 |
62 |
154.01 |
150.9 |
127.1 |
23.8 |
63 |
156.05 |
157.9 |
128.4 |
29.5 |
64 |
156.52 |
154.3 |
129.9 |
24.4 |
65 |
158.14 |
155.5 |
132.3 |
23.2 |
66 |
159.03 |
156.8 |
132.1 |
24.7 |
67 |
160.25 |
157.4 |
133.2 |
24.2 |
68 |
161.53 |
159.2 |
137.1 |
22.1 |
69 |
162.39 |
160.2 |
135.9 |
24.3 |
70 |
164 |
161 |
137.8 |
23.2 |
71 |
164.54 |
162.2 |
137.8 |
24.4 |
72 |
166.46 |
166.7 |
138.3 |
28.4 |
73 |
166.7 |
165.2 |
142.7 |
22.5 |
74 |
168.81 |
169 |
145 |
24 |
75 |
168.85 |
168.3 |
143.1 |
25.2 |
76 |
170.59 |
169.5 |
144.4 |
25.1 |
77 |
171 |
165.6 |
146.4 |
19.2 |
78 |
172.39 |
171.2 |
147.5 |
23.7 |
79 |
173.13 |
171.3 |
150.6 |
20.7 |
80 |
174.21 |
170.6 |
151.8 |
18.8 |
81 |
175.24 |
174 |
152.3 |
21.7 |
82 |
176.04 |
175.5 |
153.8 |
21.7 |
83 |
177.34 |
174.9 |
151.8 |
23.1 |
84 |
177.87 |
177.6 |
152.5 |
25.1 |
85 |
179.4 |
178.5 |
157.3 |
21.2 |
86 |
179.7 |
177.1 |
156 |
21.1 |
87 |
181.44 |
178.9 |
158.1 |
20.8 |
88 |
181.52 |
179.6 |
160.1 |
19.5 |
89 |
183.15 |
181.1 |
159 |
22.1 |
90 |
183.33 |
182.8 |
163.3 |
19.5 |
91 |
184.68 |
184.2 |
162.3 |
21.9 |
92 |
185.13 |
183.4 |
162.5 |
20.9 |
93 |
186.21 |
187.5 |
165.1 |
22.4 |
94 |
186.9 |
185.3 |
160.5 |
24.8 |
95 |
187.75 |
188.6 |
164.8 |
23.8 |
96 |
188.66 |
186.4 |
167.1 |
19.3 |
97 |
189.29 |
187.6 |
168 |
19.6 |
98 |
190.39 |
188.9 |
167.7 |
21.2 |
99 |
190.82 |
187.8 |
169.8 |
18 |
100 |
192.1 |
190.7 |
168.4 |
22.3 |
101 |
192.34 |
192.5 |
171.8 |
20.7 |
102 |
193.78 |
192.6 |
170 |
22.6 |
103 |
193.86 |
193.2 |
170.7 |
22.5 |
104 |
195.24 |
194.1 |
170 |
24.1 |
105 |
195.35 |
192.9 |
174.1 |
18.8 |
106 |
196.52 |
195.2 |
176.8 |
18.4 |
107 |
196.84 |
194.5 |
173.4 |
21.1 |
108 |
197.79 |
194.4 |
179.1 |
15.3 |
109 |
198.3 |
195.5 |
176 |
19.5 |
110 |
199.07 |
196.7 |
179.1 |
17.6 |
111 |
199.74 |
198.7 |
181.2 |
17.5 |
112 |
200.34 |
201.1 |
178.2 |
22.9 |
113 |
201.17 |
197.9 |
180.9 |
17 |
114 |
201.6 |
200.3 |
181.2 |
19.1 |
115 |
202.57 |
202 |
183.2 |
18.8 |
116 |
202.85 |
201.6 |
181 |
20.6 |
117 |
203.94 |
201.7 |
181.4 |
20.3 |
118 |
204.09 |
201.2 |
183.6 |
17.6 |
119 |
205.29 |
205.9 |
185 |
20.9 |
120 |
205.32 |
201.3 |
186.8 |
14.5 |
121 |
206.4 |
204 |
182.2 |
21.8 |
122 |
206.53 |
203.7 |
186.2 |
17.5 |
123 |
207.44 |
205.7 |
186.1 |
19.6 |
124 |
207.72 |
205.2 |
189.5 |
15.7 |
125 |
208.48 |
203.9 |
191.4 |
12.5 |
126 |
208.9 |
209.3 |
188 |
21.3 |
127 |
209.52 |
206.7 |
187.7 |
19 |
128 |
210.06 |
209.5 |
188.5 |
21 |
129 |
210.54 |
206.5 |
192.4 |
14.1 |
130 |
211.2 |
211.1 |
190.9 |
20.2 |
131 |
211.56 |
207.1 |
195.6 |
11.5 |
132 |
212.32 |
210.3 |
194 |
16.3 |
133 |
212.57 |
212.1 |
191.1 |
21 |
134 |
213.42 |
211 |
192.7 |
18.3 |
135 |
213.56 |
210.2 |
195.8 |
14.4 |
136 |
214.5 |
213.3 |
196.8 |
16.5 |
137 |
214.55 |
211.3 |
194.4 |
16.9 |
138 |
215.46 |
212 |
196.6 |
15.4 |
139 |
215.52 |
210.8 |
197.4 |
13.4 |
140 |
216.3 |
215.3 |
197 |
18.3 |
141 |
216.47 |
217.8 |
199.3 |
18.5 |
142 |
217.13 |
215.4 |
197.3 |
18.1 |
143 |
217.41 |
214.8 |
196.2 |
18.6 |
144 |
217.96 |
213.9 |
200.1 |
13.8 |
145 |
218.33 |
215.7 |
200.4 |
15.3 |
146 |
218.77 |
217.4 |
200.1 |
17.3 |
147 |
219.24 |
217.5 |
199.7 |
17.8 |
148 |
219.58 |
218.5 |
200.3 |
18.2 |
149 |
220.13 |
218.4 |
200.3 |
18.1 |
150 |
220.39 |
220.4 |
201.9 |
18.5 |
151 |
221 |
218.1 |
201.6 |
16.5 |
152 |
221.18 |
220.5 |
203.9 |
16.6 |
153 |
221.86 |
220.6 |
202.6 |
18 |
154 |
221.96 |
220.5 |
205.2 |
15.3 |
155 |
222.69 |
218.7 |
203.1 |
15.6 |
156 |
222.72 |
220.6 |
204.4 |
16.2 |
157 |
223.43 |
220.6 |
203.3 |
17.3 |
158 |
223.48 |
221.1 |
202.8 |
18.3 |
159 |
224.09 |
222.6 |
207.1 |
15.5 |
160 |
224.22 |
224.5 |
207.5 |
17 |
161 |
224.74 |
220.8 |
206 |
14.8 |
162 |
224.95 |
224.2 |
208.1 |
16.1 |
163 |
225.39 |
223.8 |
208 |
15.8 |
164 |
225.67 |
222.8 |
209 |
13.8 |
165 |
226.03 |
223.4 |
208.6 |
14.8 |
166 |
226.37 |
224 |
210 |
14 |
167 |
226.66 |
225.3 |
209.2 |
16.1 |
168 |
227.06 |
224.1 |
211.6 |
12.5 |
169 |
227.28 |
224.5 |
210.5 |
14 |
170 |
227.73 |
223.8 |
211 |
12.8 |
171 |
227.89 |
226.9 |
209.1 |
17.8 |
172 |
228.39 |
226 |
212.2 |
13.8 |
173 |
228.49 |
226 |
211.8 |
14.2 |
174 |
229.04 |
226.6 |
212.1 |
14.5 |
175 |
229.09 |
227.9 |
211.3 |
16.6 |
176 |
229.67 |
226.4 |
211.5 |
14.9 |
177 |
229.67 |
228 |
214 |
14 |
178 |
230.18 |
228.4 |
215.1 |
13.3 |
179 |
230.24 |
227.5 |
213.3 |
14.2 |
180 |
230.68 |
229.2 |
213.6 |
15.6 |
181 |
230.8 |
229.5 |
215 |
14.5 |
182 |
231.18 |
228.7 |
213.9 |
14.8 |
183 |
231.36 |
229.8 |
216 |
13.8 |
184 |
231.67 |
230.6 |
214.4 |
16.2 |
185 |
231.9 |
231 |
213.1 |
17.9 |
186 |
232.16 |
231.2 |
216.2 |
15 |
189 |
232.94 |
231.1 |
217.9 |
13.2 |
190 |
233.1 |
230.4 |
217.6 |
12.8 |
191 |
233.45 |
231.1 |
218.4 |
12.7 |
192 |
233.56 |
231.9 |
219 |
12.9 |
193 |
233.94 |
232.1 |
216.6 |
15.5 |
194 |
234.02 |
232 |
219.3 |
12.7 |
195 |
234.43 |
231.8 |
217.5 |
14.3 |
196 |
234.47 |
232.4 |
220.6 |
11.8 |
197 |
234.9 |
233.5 |
218.6 |
14.9 |
198 |
234.9 |
233 |
219.3 |
13.7 |
199 |
235.3 |
233.4 |
220.2 |
13.2 |
200 |
235.33 |
233.8 |
221.1 |
12.7 |
201 |
235.67 |
235.5 |
218.8 |
16.7 |
202 |
235.75 |
233 |
222 |
11 |
203 |
236.05 |
232.9 |
220.4 |
12.5 |
204 |
236.17 |
233.9 |
220.1 |
13.8 |
205 |
236.42 |
234.8 |
221 |
13.8 |
206 |
236.57 |
234.4 |
221.4 |
13 |
207 |
236.78 |
234.8 |
222.6 |
12.2 |
208 |
236.96 |
236.4 |
222.5 |
13.9 |
209 |
237.14 |
234.6 |
223.5 |
11.1 |
210 |
237.35 |
236.6 |
222.6 |
14 |
211 |
237.49 |
235.7 |
221.9 |
13.8 |
212 |
237.73 |
234.4 |
222.4 |
12 |
213 |
237.83 |
234.9 |
226 |
8.9 |
214 |
238.1 |
237.3 |
223.9 |
13.4 |
215 |
238.17 |
237 |
223.6 |
13.4 |
216 |
238.46 |
235.7 |
225.1 |
10.6 |
217 |
238.5 |
236.6 |
223.6 |
13 |
218 |
238.81 |
237 |
226.1 |
10.9 |
219 |
238.83 |
236.4 |
225 |
11.4 |
220 |
239.15 |
237.7 |
225.7 |
12 |
221 |
239.15 |
236.8 |
225.9 |
10.9 |
222 |
239.43 |
237.7 |
225.9 |
11.8 |
223 |
239.46 |
238.6 |
224.8 |
13.8 |
224 |
239.71 |
237.1 |
226.3 |
10.8 |
225 |
239.77 |
238.7 |
227.4 |
11.3 |
226 |
239.98 |
238.7 |
225.9 |
12.8 |
227 |
240.07 |
238 |
226.9 |
11.1 |
228 |
240.25 |
240.5 |
227.6 |
12.9 |
229 |
240.36 |
238.8 |
227.5 |
11.3 |
230 |
240.51 |
237.9 |
225.8 |
12.1 |
231 |
240.65 |
238.5 |
228.2 |
10.3 |
232 |
240.77 |
239.3 |
226.6 |
12.7 |
233 |
240.92 |
238.8 |
226.1 |
12.7 |
234 |
241.03 |
240.2 |
228.8 |
11.4 |
235 |
241.2 |
240.4 |
227.5 |
12.9 |
236 |
241.28 |
240 |
227.4 |
12.6 |
237 |
241.46 |
239.8 |
228 |
11.8 |
238 |
241.52 |
240.6 |
228.8 |
11.8 |
239 |
241.72 |
240.1 |
228.7 |
11.4 |
240 |
241.76 |
240.2 |
229.2 |
11 |
241 |
241.98 |
240.3 |
229.2 |
11.1 |
242 |
242 |
240.7 |
229.3 |
11.4 |
243 |
242.22 |
240.5 |
229.7 |
10.8 |
244 |
242.23 |
239.9 |
229.2 |
10.7 |
245 |
242.44 |
241.2 |
230.3 |
10.9 |
246 |
242.45 |
240.7 |
230.5 |
10.2 |
247 |
242.64 |
241.3 |
231.5 |
9.8 |
248 |
242.68 |
239.2 |
230.4 |
8.79 |
249 |
242.84 |
241.5 |
230.3 |
11.2 |
250 |
242.89 |
241.4 |
230.6 |
10.8 |
251 |
243.03 |
242.2 |
230.4 |
11.8 |
252 |
243.1 |
241.7 |
232.3 |
9.39 |
253 |
243.22 |
242.6 |
232.2 |
10.4 |
254 |
243.31 |
241 |
229.7 |
11.3 |
255 |
243.41 |
240.7 |
231.1 |
9.59 |
256 |
243.51 |
242.2 |
231 |
11.2 |
257 |
243.59 |
241 |
232.4 |
8.59 |
258 |
243.7 |
242.1 |
230.2 |
11.9 |
259 |
243.77 |
242 |
232.1 |
9.90 |
260 |
243.9 |
243.2 |
230.4 |
12.8 |
261 |
243.95 |
242.9 |
233.6 |
9.30 |
262 |
244.08 |
242.6 |
233.6 |
9 |
263 |
244.12 |
243 |
231.3 |
11.7 |
264 |
244.26 |
242.3 |
233.5 |
8.80 |
265 |
244.29 |
241.8 |
233.8 |
8 |
266 |
244.44 |
242.9 |
233.1 |
9.80 |
267 |
244.46 |
242.6 |
233.8 |
8.79 |
268 |
244.61 |
242.9 |
234 |
8.90 |
269 |
244.62 |
244 |
234.3 |
9.69 |
270 |
244.76 |
243.6 |
234.4 |
9.19 |
271 |
244.77 |
243.6 |
235 |
8.59 |
272 |
244.91 |
243.2 |
234.7 |
8.5 |
273 |
244.93 |
243.9 |
233.2 |
10.7 |
274 |
245.04 |
243.5 |
233.5 |
10 |
275 |
245.08 |
243.7 |
234.2 |
9.5 |
276 |
245.18 |
243.4 |
234.8 |
8.59 |
277 |
245.23 |
244.2 |
234.2 |
10 |
278 |
245.31 |
244.8 |
234.8 |
10 |
279 |
245.37 |
244.1 |
234.7 |
9.40 |
280 |
245.44 |
243.7 |
234.1 |
9.59 |
281 |
245.51 |
244.1 |
234 |
10.1 |
282 |
245.57 |
243.6 |
235.8 |
7.79 |
283 |
245.65 |
243.8 |
235.3 |
8.5 |
284 |
245.7 |
244 |
235 |
9 |
285 |
245.78 |
244.3 |
236.9 |
7.40 |
286 |
245.82 |
243.7 |
235 |
8.69 |
287 |
245.91 |
244.6 |
236.2 |
8.40 |
288 |
245.94 |
244.7 |
235.4 |
9.29 |
289 |
246.04 |
245.2 |
237.3 |
7.89 |
290 |
246.06 |
244.6 |
234.8 |
9.79 |
291 |
246.16 |
243.8 |
235.6 |
8.20 |
292 |
246.17 |
244.8 |
236.2 |
8.60 |
293 |
246.28 |
244.6 |
236.2 |
8.40 |
294 |
246.29 |
245.2 |
236.9 |
8.29 |
295 |
246.39 |
245.2 |
237.2 |
8 |
296 |
246.39 |
245.2 |
236.5 |
8.69 |
297 |
246.49 |
245.1 |
235.7 |
9.40 |
298 |
246.5 |
244.9 |
237.4 |
7.5 |
299 |
246.59 |
245.4 |
237.5 |
7.90 |
300 |
246.61 |
246 |
236.2 |
9.80 |
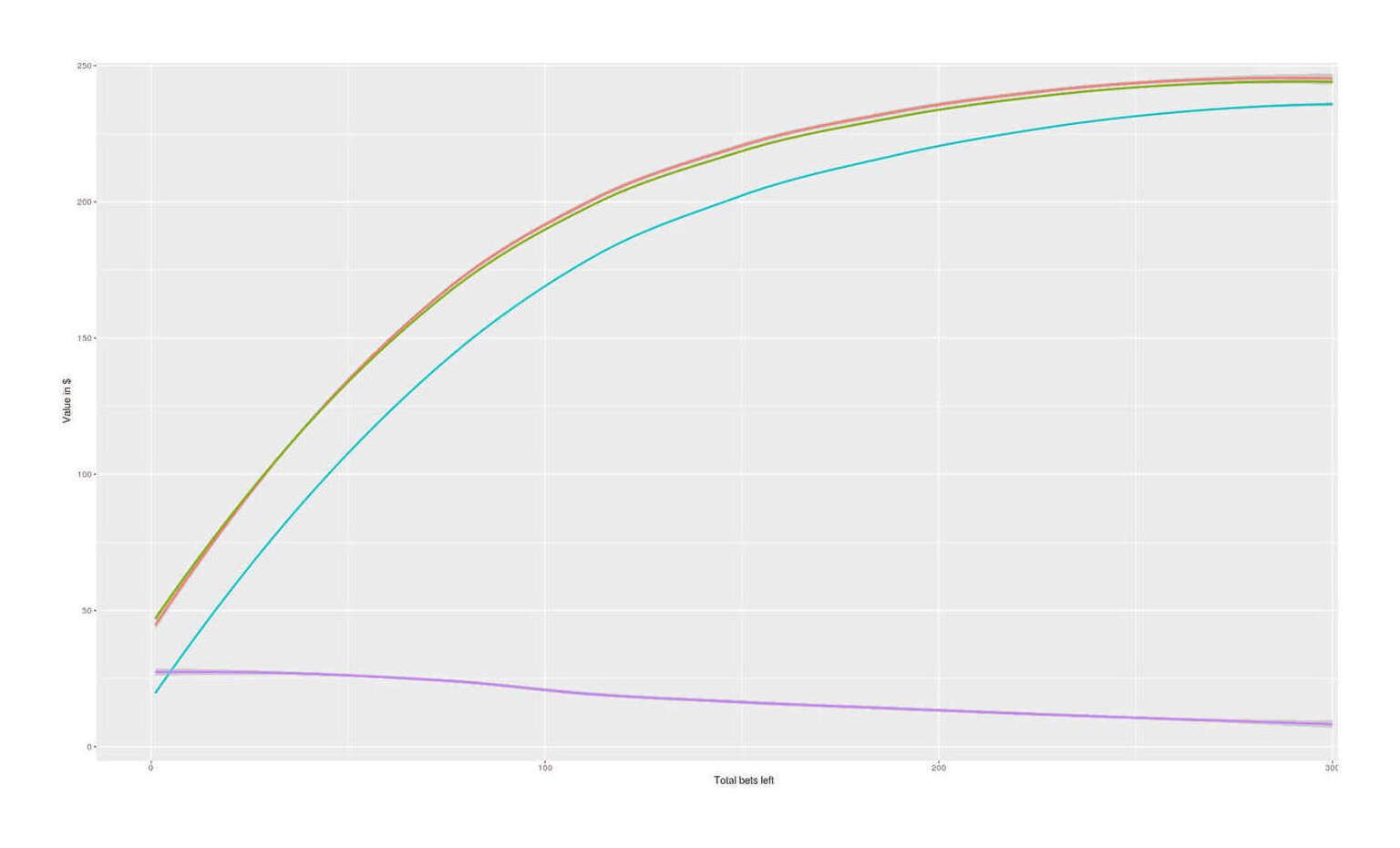
Performance of modified Kelly criterion versus theoretical optimal performance versus decision-tree performance
So the decision tree does outperform the 20% KC, and not by trivial amounts either, in relative or absolute terms: for b = 23, the estimated gain is $37.1. The decision tree doesn’t require the full b = 300 to often hit the ceiling, although the KC will. However, the performance edge goes down as the horizon gets more distant, and we’ll see that as far out as b = 300, the advantage shrinks to ~$6 as the ceiling is hit almost all the time by decent strategies (as we know from the 2016 analysis that KC hits the ceiling ~95% of the time with b = 300, although of course it will do so far less often for shorter runs like b = 50).
Since the 20% KC was only suggested as a heuristic, one might wonder if there’s a different constant fraction which does slightly better in the b = 300 case, which there is, 12%:
fraction <- seq(0,1, by=0.01)
fractionEVs <- ldply(mclapply(fraction, function(f) {
k <- function(w,b) { if(w==250) {0} else { f * w } }
kev <- simulateGame(k, b=300)
return(kev) }
))
fraction[which.max(unlist(fractionEVs))]
# [1] 0.12
qplot(fraction, fractionEVs)Generalized Kelly Coin-Flip Game: POMDPs
The original Kelly coinflip game has a clear way to make it more general and difficult: randomize the 3 key parameters of edge/max wealth/rounds and hide them, turning it into a partially observable Markov decision process.
To solve a POMDP one often has to record the entire history, but with judicious choice of what distribution we randomize the 3 parameters from, we can make it both plausibly reflecting the human subjects’ expectations and allow summarizing the history in a few sufficient statistics.
Implementation
A Python implementation with the suggested randomizations is available in OpenAI Gym:
import gym
env = gym.make('KellyCoinflipGeneralized-v0')
env.reset()
env._render() # peek at the hidden parameters
env._step(env.wealth*100*0.2)
# ...
env._reset() # etcBayesian Decision Tree
Unknown Coin-Flip Probability
A variant on this problem is when the probability of winning is not given, if one doesn’t know in advance p = 0.6. How do you make decisions as coin flips happen and provide information on p? Since p is unknown and only partially observed, this turns the coin-flip MDP into a POMDP problem. A POMDP can be turned back into a MDP and solved in a decision tree by including the history of observations as more parameters to explore over.
The curse of dimensionality can be tamed here a little by observing that a history of coin-flip sequences is unnecessary—it doesn’t matter what order the coin flips happen in, only the number of wins and the number of total coin-flips matter (are the sufficient statistics). So we only need to augment wealth/rounds/bet-amount with wins/n. And one can compute p from wins/n by Bayesian updates of a prior on the observed coin flip results, treating it as a binomial problem of estimating p distributed according to the beta distribution.
This beta Bayesian update is easy and doesn’t require calling out to a library: with a beta uniform prior (Beta(1,1)), update on binomial (win/loss) is conjugate with the simple closed form posterior of Beta(1+win, 1+n-win); and the expectation of the beta is 1+win / 1+n. Then our expected values in f simply change from 0.6/0.4 to expectation/1-expectation.
Going back to the R implementation, we add in the two additional parameters, the beta estimation, and estimate the hardwired probabilities:
library(memoise)
f <- function(x, w, b, wins, n) {
beta <- c(1+wins, 1+n-wins)
expectedWinProb <- beta[1] / (beta[1]+beta[2]) # E[Beta(alpha, beta)] = alpha / (alpha+beta)
expectedLoseProb <- 1 - expectedWinProb
expectedWinProb*mV(min(w+x,250), b-1, wins+1, n+1) + expectedLoseProb*mV(w-x, b-1, wins, n+1) }
mf <- memoise(f)
V <- function(w,b,wins,n) {
returns <- if (b>0 && w>0 && w<250) { sapply(seq(0, w, by=0.1), function(x) { mf(x,w,b, wins, n) }) } else { w }
max(returns) }
mV <- memoise(V)What prior should we use?
Ideally we would use the prior of the participants in the experiment, to compare how well they do compared to the Bayesian decision tree, and estimate how much mistaken beliefs cost them. Unfortunately they were not surveyed on this and the authors do not give any indication of how much of an edge the subjects expected before starting the game, so for analysis, we’ll make up a plausible prior.
We know that they know that 100% is not an option (as that would be boring) and <50% is impossible too since they were promised an edge; but it can’t be too high because then everyone would win quickly and nothing would be learned. I think a reasonable prior would be something like 70%, but with a lot of room for surprise. let’s assume a weak prior around 70%, which is equivalent to playing 10 games and winning 7, so Beta(7, 3).
With the additional parameters, the memoized version becomes impossibly slow, so I rewrite it to use R environments as a poor man’s hash table:
tree <- new.env(size=1000000, parent=emptyenv())
f <- function(x, w, b, wins, n) {
beta <- c(1+wins, 1+n-wins)
expectedWinProb <- beta[1] / (beta[1]+beta[2]) # E[Beta(alpha, beta)] = alpha / (alpha+beta)
expectedLoseProb <- 1 - expectedWinProb
expectedWinProb*V(min(w+x,250), b-1, wins+1, n+1) + expectedLoseProb*V(w-x, b-1, wins, n+1) }
V <- function(w, b, wins, n) {
if (isSet(c(w,b,wins,n))) { return(lookup(c(w,b,wins,n))) } else {
returns <- if (b>0 && w>0 && w<250) { sapply(seq(0, w, by=0.1), function(x) { f(x,w,b,wins,n) }) } else { return(w) }
set(c(w,b,wins,n), max(returns))
return(lookup(c(w,b,wins,n)))
}
}
# test expression: $25, 5 bets, suggested 7⁄10 prior:
V(25,5,7,10)This prior leads to somewhat more aggressive betting in short games as the EV is higher, but overall performs much like the decision tree.
nshepperd provides a modified version of his code which lets us evaluate up to b = 300:
{-# LANGUAGE ScopedTypeVariables #-}
import System.Environment
import Data.List
import Data.Foldable
import Data.Function
import Data.Function.Memoize
import Data.Vector (Vector)
import qualified Data.Vector as V
import Data.Ord
import Text.Printf
import Numeric.Search.Range -- from 'binary-search'
type Wealth = Int
type BetAmount = Wealth
type Probability = Double
type EV = Double
type Round = Int
type MaxRounds = Round
type WonRounds = Round
type Alpha = Int
type Beta = Int
cap :: Wealth
cap = 250
data Tree = Done EV
| Bet EV Wealth BetAmount Round Probability Tree Tree
deriving (Show)
data Dual = Dual {
subjectiveEV :: !EV,
trueEV :: !EV
} deriving (Show)
instance Plan Dual where
done w = Dual (fromIntegral w) (fromIntegral w)
bet w x b p win loss = Dual {
subjectiveEV = p * subjectiveEV win + (1 - p) * subjectiveEV loss,
trueEV = 0.6 * trueEV win + (1 - 0.6) * trueEV loss
}
strategyEV = subjectiveEV
class Plan s where
done :: Wealth -> s
bet :: Wealth -> BetAmount -> Round -> Double -> s -> s -> s
strategyEV :: s -> EV
instance Plan Double where
done = fromIntegral
bet w x b p win loss = p * win + (1 - p) * loss
strategyEV = id
instance Plan Tree where
done w = Done (fromIntegral w)
strategyEV (Done ev) = ev
strategyEV (Bet ev _ _ _ _ _ _) = ev
bet 0 _ _ _ _ _ = Done 0
bet w x b p win loss = Bet ev w x b p win loss
where
ev = p * strategyEV win + (1 - p) * strategyEV loss
showTree :: Tree -> String
showTree (Done ev) = show (Done ev)
showTree (Bet ev w x b p win loss) = intercalate "\n" [
printf "%i (%1.1f): %i/%i at %2.2f" b ev x w p,
indent 4 ("+ " ++ showTree win),
indent 4 ("- " ++ showTree loss)
]
where
indent n str = intercalate "\n" $ map (replicate n ' ' ++) $ lines str
-- $ Unordered maximum
maximumOn :: (Foldable f, Ord b) => (a -> b) -> f a -> a
maximumOn f = maximumBy (comparing f)
-- Binary search on bitonic function.
maximumBitonic :: Ord b => (a -> b) -> Vector a -> a
maximumBitonic f options = case searchFromTo find 0 (V.length options - 2) of
Just i -> options V.! i
Nothing -> options V.! (V.length options - 1)
where
find i = f (options V.! i) >= f (options V.! (i + 1))
value :: Plan s
=> Alpha -> Beta -> MaxRounds
-> (Round -> WonRounds -> Wealth -> s)
-> (Round -> WonRounds -> Wealth -> s)
value alpha beta lastRound next currentRound wins w
| currentRound >= lastRound = done w
| w >= cap = done w
| otherwise = maximumBitonic strategyEV options
where
new_alpha = alpha + wins
new_beta = beta + (currentRound - wins)
p = fromIntegral new_alpha / fromIntegral (new_alpha + new_beta)
go x = bet w x currentRound p
(next (currentRound+1) (wins+1) (w+x))
(next (currentRound+1) wins (w-x))
options = V.fromList [go x | x <- [0..min (cap - w) w]]
-- Direct recursion.
direct :: Plan s
=> Alpha -> Beta -> MaxRounds
-> (Round -> WonRounds -> Wealth -> s)
direct a b m = fix (value a b m)
-- Memoized recursion.
memo :: forall s. Plan s
=> Alpha -> Beta -> MaxRounds
-> (Round -> WonRounds -> Wealth -> s)
memo a b maxRounds = cached_value
where
cached_value r wins w = table V.! r V.! wins V.! w
table :: Vector (Vector (Vector s))
table = V.generate (maxRounds + 1)
(\r -> V.generate (r + 1)
(\wins -> V.generate (cap + 1)
(\w -> value a b maxRounds cached_value r wins w)))
-- Memoized recursion using 'memoize' library; slower.
memo2 :: Plan s
=> Alpha -> Beta -> MaxRounds
-> (Round -> WonRounds -> Wealth -> s)
memo2 a b r = memoFix3 (value a b r)
run :: Plan s
=> (alpha -> beta -> maxRounds -> (Round -> WonRounds -> wealth -> s))
-> alpha -> beta -> maxRounds -> wealth -> s
run method alpha beta rounds w = method alpha beta rounds 0 0 w
main :: IO ()
main = do [a, b, r, w] <- map read <$> getArgs
print $ (run memo a b r w :: Dual)One feature offered by this code is reporting two expected-values:
the subjective estimate of the agent at the beginning of the game about how much it can profit, given the rules and its priors about p
the EV it will actually earn, following its policy, given the true probability p = 0.6
For our prior, w = 25, and b = 300, we can evaluate run memo (7+1) (3+1) 300 25 :: Dual and find that the subjective EV is $207.238 and the actual EV is $245.676.
And since we know from earlier that an agent following the optimal policy believing p = 0.6 would earn $246.606, it follows that the Bayesian agent, due to its ignorance, loses ~$1. So the price of ignorance (regret) in this scenario is surprisingly small.
Why is the Bayesian decision tree able to perform so close to the known-probability decision tree? I would guess that it is because all agents bet small amounts in the early rounds (to avoid gambler’s ruin, since they have hundreds of rounds left to reach the ceiling), and this gives them data for free to update towards p = 0.6; the agent which knows that p = 0.6 can bet a little more precisely early on, but this advantage over a few early rounds doesn’t wind up being much of a help in the long run.
With b = 300, there are so many rounds available to bet, that the details don’t matter as much; while it there are only a few bets, the maximizing behavior is to bet a lot so the regret for small b is also probably small; the largest regret for not knowing p is probably somewhere, like with the KC vs decision tree, in the small-medium area of b.
Unknown Stopping Time
Another variant would be to make the stopping time uncertain; strictly speaking, the game wasn’t fixed at exactly 300 rounds, that was just their guess at how many rounds a reasonably fast player might get in before the clock expired. From the player’s perspective, it is unknown how many rounds they will get to play although they can guess that they won’t be allowed to play more than a few hundred, and this might affect the optimal strategy.
One way to calculate this would be to assume that the player doesn’t learn anything about the stopping time while playing, and merely has a prior over the stopping time. For example, 𝒩(300,25). The game stopping can be seen as a third probabilistic response to a player’s bet, where each move with some sp, if it happens the number of bets left immediately becomes b = 0 (so they win their current w) and they win the net value V(w,0); and if it doesn’t happen the value is the usual 0.6*V(w+x, b-1) + 0.4*V(w-x, b-1). Or in longer form, the value of an action/bet x is (1-sp)*(0.6*V(w+x,b-1) + 0.4*V(w-x,b-1)) + sp*V(w,0).
What is sp as a distribution? Well, one might believe that every round, there is a ~1% chance of the game stopping, in which case sp is the memoryless geometric distribution (not exponential distribution, since this is a discrete setup); in this case, one must discount each additional round n by 1% cumulatively. (Discounting in general could be seen as reflecting a probability of stopping at each stage.)
This has the difficulty that hypothetically, a game might go on indefinitely long, but since a player must eventually hit $0 or $250 and stop playing, it would turn out like the penny simulator—after a few thousand rounds, the probability of having not reached $250 is so small it can’t be handled by most software. The problem is more that this expands the states out enough to again make it unevaluable, so it helps to put an upper bound. So the problem becomes, playing the game knowing that the game might stop with a certain sp (eg. 0.01) each round or stops at an upper limit number of rounds (eg. b = 300).
So continuing with the R hash table, it might go like this:
f <- function(x, w, b) {
sp <- 0.01
(1-sp)*(0.6*V(min(250,w+x), b-1) + 0.4*V(w-x,b-1)) + sp*V(w,0)
}
V <- function(w, b) {
if (isSet(c(w,b))) { return(lookup(c(w,b))) } else {
returns <- if (b>0 && w>0 && w<250) { sapply(seq(0, w, by=0.1), function(x) { f(x,w,b) }) } else { return(w) }
set(c(w,b), max(returns))
return(lookup(c(w,b)))
}
}This can be extended to scenarios where we do learn something about the stopping time, similarly to the coin-flip probability, by doing Bayesian updates on sp. Or if sp changes over rounds. If we had a distribution 𝒩(300,25) over the stopping time, then the probability of stopping at each round can change inside the value function given an additional argument n for rounds elapsed as the sufficient statistic.
Unknown Maximum Wealth Cap
Finally, subjects weren’t told what the maximum would be:
The maximum payout would be revealed if and when subjects placed a bet that if successful would make their balance greater than or equal to the cap. We set the cap at $250.
A convenient distribution for such a cap would be the Pareto distribution, parameterized by a minimum xm and a tail parameter, α. If xm is set to something like 100 (the agent thinks the cap is >$100), for most rounds, the agent would not be able to update this, but towards the end, as it exceeds $100, it then updates the posterior—if it is allowed to make a bet of $50 at $100, then xm becomes 150 while α remains the same, and so on. In this case, the maximum observed wealth is the sufficient statistic. The posterior mean of the cap is then {α × xm) / (α − 1). A reasonable prior might be α=5 and xm = 200, in which case the mean wealth cap is 250.
f <- function(x, w, b, alpha, x_m) {
meanCap <- (alpha * x_m) / (alpha-1) # mean posterior cap if our bet does not threaten to hit the cap
x_m_updated <- max(x_m, x+w)
meanCapUpdated <- (alpha * x_m_updated) / (alpha-1) # mean posterior cap if our bet does threaten to hit the cap
Pcap <- if ((x+b) < x_m) { 0 } else { 1-((x_m / (x+b))^alpha) } # CDF
(1-Pcap)*(0.6*V(min(meanCap,w+x), b-1, alpha, x_m) + 0.4*V(w-x,b-1,alpha,x_m)) +
Pcap*(0.6*V(min(meanCapUpdated,w+x), b-1, alpha, x_m_updated) + 0.4*V(w-x,b-1,alpha,x_m_updated))
}
V <- function(w, b, alpha=5, x_m=200) {
if (isSet(c(w,b,alpha,x_m))) { return(lookup(c(w,b,alpha,x_m))) } else {
returns <- if (b>0 && w>0) { sapply(seq(0, w, by=0.1), function(x) { f(x,w,b,alpha,x_m) }) } else { return(w) }
set(c(w,b,alpha,x_m), max(returns))
return(lookup(c(w,b,alpha,x_m)))
}
}Value of POMDP
What is the value of this full POMDP game with uncertain wealth cap, stopping time, and edge?
Upper Bound
We can approximate it with our pre-existing value function for a known stopping time/edge/max wealth, sampling from the posterior; for example, we might draw 1000 values from 𝒩(300,25), the Pareto, the Beta etc, calculate the value of each set of parameters, and taking the mean value. Since the value of information is always zero or positive, the value of the POMDP with known parameters must be an upper bound on its true value, since we can only do worse in each game by being ignorant of the true parameters and needing to infer them as we play; so if we calculate a value of $240 or whatever, we know the POMDP must have a value <$240, and that gives a performance target to aim for.
The Haskell version is the easiest to work with, but Haskell doesn’t have convenient distributions to sample from, so instead I generate 1000 samples from the prior distribution of parameters in Python (reusing some of the Gym code):
from scipy.stats import genpareto
import numpy as np
import numpy.random
from gym.spaces import prng
edgePriorAlpha=7
edgePriorBeta=3
maxWealthAlpha=5
maxWealthM=200
maxRoundsMean=300
maxRoundsSD=25
for i in xrange(0,1000):
edge = prng.np_random.beta(edgePriorAlpha, edgePriorBeta)
maxWealth = int(round(genpareto.rvs(maxWealthAlpha, maxWealthM, random_state=prng.np_random)))
maxRounds = int(round(prng.np_random.normal(maxRoundsMean, maxRoundsSD)))
print 25, maxRounds, edge, maxWealthand then we can modify nshepperd’s Haskell code to allow the edge and wealth cap to be modifiable, and then we simply run memo over the 1000 possible sets of parameters, and take the mean. Using the raw samples turns out to be infeasible in terms of RAM, probably because higher wealth caps (which are Pareto distributed and can be extremely large) increases dimensionality too much to evaluate in my ~25GB RAM, so the wealth cap itself must be shrunk, to TODO $1,000? which unfortunately muddles the meaning of the estimate since now it’s a lower bound of an upper bound, or to reverse it, value of clairvoyant play assuming that many games have a lower wealth cap than they do.
import Data.Vector (Vector)
import qualified Data.Vector as V (generate, (!))
type Wealth = Int
type Bets = Int
type Edge = Double
type Cap = Int
type EV = Double
value :: (Wealth -> Bets -> EV) -> Wealth -> Bets -> Edge -> Cap -> EV
value _ 0 _ _ _ = 0
value _ w 0 _ _ = fromIntegral w
value next w b e cap = maximum [go x | x <- [0..min (cap - w) w]]
where
go x = e * next (min cap (w+x)) (b-1) + (1-e) * next (w-x) (b-1)
memo :: Wealth -> Bets -> Edge -> Cap -> EV
memo w b e cp = cached_value w b
where
cached_value w' b' = table V.! b' V.! w'
table :: Vector (Vector EV)
table = V.generate (b + 1)
(\b'' -> V.generate (cp + 1)
(\w'' -> value cached_value w'' b'' e cp))
main :: IO ()
main = do let evs = map (\(w,b,e,cap) -> memo w b e cap) parameters
print evs
print $ mean evs
where mean x = sum x / fromIntegral (length x)
maxCap :: Int
maxCap = 800
parameters :: [(Wealth, Bets, Edge, Cap)]
parameters = map (\(w,b,e,c) -> (w,b,e, max maxCap c)) [(25, 236, 0.72435085557, 205), (25, 237, 0.845435411107, 260), (25, 238, 0.413782110845, 202),
(25, 240, 0.345133535603, 23999), (25, 240, 0.400147029568, 2521), (25, 242, 0.661912880989, 201), (25, 242, 0.676168121514, 6740),
(25, 242, 0.701381545443, 1726), (25, 242, 0.849537381053, 203), (25, 242, 0.898462493046, 201), (25, 243, 0.54257657328, 201),
(25, 245, 0.77972062792, 48534), (25, 246, 0.813395396485, 203), (25, 247, 0.480134063147, 214), (25, 247, 0.533273012857, 222),
(25, 247, 0.754222974601, 201), (25, 249, 0.70782818171, 200), (25, 249, 0.748310452532, 202), (25, 251, 0.606478140487, 200),
(25, 251, 0.809355705263, 526), (25, 252, 0.524864167122, 200), (25, 252, 0.749206398756, 352321), (25, 252, 0.822818892461, 201),
(25, 253, 0.542598606499, 201), (25, 253, 0.600469152584, 200), (25, 253, 0.648598435209, 219), (25, 253, 0.649453264073, 2589),
(25, 253, 0.679414549454, 28311200), (25, 253, 0.86227613481, 202), (25, 254, 0.585056497076, 2575033),
(25, 254, 0.680452842612, 200), (25, 255, 0.877950348346, 201), (25, 256, 0.643298850757, 205), (25, 256, 0.712973552037, 204),
(25, 256, 0.718153926517, 201), (25, 256, 0.813126205309, 201), (25, 256, 0.8280445068, 208), (25, 257, 0.402688232643, 201),
(25, 257, 0.548591912297, 651), (25, 257, 0.601967601919, 206), (25, 257, 0.862541920316, 200), (25, 257, 0.863389650382, 200),
(25, 258, 0.474519595118, 213), (25, 258, 0.735744534702, 208), (25, 258, 0.738339372201, 360), (25, 258, 0.84277195943, 83144),
(25, 258, 0.93190614133, 2409618061), (25, 259, 0.471094149142, 745), (25, 260, 0.628797799899, 202), (25, 260, 0.710033767475, 9552510),
(25, 260, 0.813466187199, 200), (25, 261, 0.550748996178, 230), (25, 261, 0.629544256918, 259), (25, 261, 0.683386138653, 200),
(25, 261, 0.792209742213, 201), (25, 261, 0.794533480259, 207), (25, 262, 0.344887568623, 201), (25, 262, 0.450645011078, 473),
(25, 262, 0.738248174312, 225), (25, 262, 0.791527693933, 210), (25, 262, 0.832198167412, 200), (25, 263, 0.35093259949, 203),
(25, 263, 0.521818533732, 366), (25, 263, 0.64076936694, 59847), (25, 263, 0.684063131912, 201), (25, 263, 0.714065733976, 201),
(25, 263, 0.789350373174, 1705), (25, 263, 0.829406017035, 210), (25, 263, 0.902144916794, 255), (25, 263, 0.951257247224, 202),
(25, 264, 0.32472812884, 203), (25, 264, 0.604563170498, 250), (25, 264, 0.626423177116, 22769), (25, 264, 0.871339562605, 205),
(25, 265, 0.452014126574, 200), (25, 265, 0.54226419925, 201), (25, 265, 0.625113911686, 212), (25, 265, 0.654404133816, 206),
(25, 265, 0.678345789504, 420), (25, 265, 0.771116406164, 210), (25, 265, 0.771222624754, 205), (25, 265, 0.801480809161, 200),
(25, 265, 0.806182111956, 60957), (25, 265, 0.851715904261, 18981), (25, 266, 0.685689594858, 200), (25, 266, 0.711416415881, 210),
(25, 266, 0.711937019202, 851), (25, 266, 0.724721571466, 200), (25, 266, 0.816529965664, 654), (25, 266, 0.820884461992, 287),
(25, 267, 0.798462101302, 200), (25, 267, 0.814520382826, 200), (25, 267, 0.815795664692, 201), (25, 267, 0.877810894936, 200),
(25, 268, 0.37374747435, 7152), (25, 268, 0.66383704238, 201), (25, 268, 0.671499425192, 224), (25, 268, 0.72882798744, 205),
(25, 268, 0.788161778332, 534537579002), (25, 268, 0.793723223502, 584), (25, 268, 0.83414422735, 16291),
(25, 268, 0.933374294433, 219), (25, 269, 0.460012103336, 211), (25, 269, 0.575089962258, 203), (25, 269, 0.587666214938, 213),
(25, 269, 0.617907437269, 201), (25, 269, 0.711693869892, 203), (25, 269, 0.755193420929, 200), (25, 269, 0.764409970652, 2593),
(25, 269, 0.769445254497, 6962), (25, 269, 0.781046904571, 1030), (25, 269, 0.92721940969, 2062780), (25, 269, 0.937746457329, 201),
(25, 270, 0.43758799016, 201), (25, 270, 0.55945290829, 206), (25, 270, 0.594599037706, 579), (25, 270, 0.6205174976, 506),
(25, 270, 0.660258985896, 217), (25, 270, 0.688180575479, 308), (25, 270, 0.703263135667, 201), (25, 270, 0.730492162736, 46132),
(25, 270, 0.7898205196, 25541), (25, 270, 0.893976819617, 201), (25, 270, 0.921080018968, 200), (25, 271, 0.525815069976, 200),
(25, 271, 0.554615752325, 200), (25, 271, 0.629469767651, 200), (25, 271, 0.709135907244, 9875), (25, 271, 0.759981836553, 202),
(25, 271, 0.811129692174, 91717), (25, 271, 0.837347167701, 200), (25, 271, 0.873514454515, 200), (25, 271, 0.923252939562, 208),
(25, 272, 0.556207216343, 785), (25, 272, 0.575453865622, 215), (25, 272, 0.638921822998, 200), (25, 272, 0.642223697178, 219),
(25, 272, 0.66336333735, 213), (25, 272, 0.798971543861, 209), (25, 272, 0.826187121413, 216), (25, 272, 0.864733208766, 204),
(25, 273, 0.517135630277, 200), (25, 273, 0.560438221638, 221192794), (25, 273, 0.77368870442, 883), (25, 273, 0.846232723863, 785),
(25, 273, 0.9652451074, 200), (25, 274, 0.607659170171, 339), (25, 274, 0.611760970714, 201), (25, 274, 0.638249890182, 201),
(25, 274, 0.706185385091, 201), (25, 274, 0.760147689131, 200), (25, 274, 0.804365960436, 1051), (25, 274, 0.848798405341, 1117),
(25, 275, 0.333707647765, 200), (25, 275, 0.555403709258, 205), (25, 275, 0.655942931908, 206), (25, 275, 0.676684395133, 201),
(25, 275, 0.698400431321, 203), (25, 275, 0.796131451966, 200), (25, 275, 0.840528265848, 200), (25, 275, 0.856009338181, 200),
(25, 276, 0.497611590615, 211), (25, 276, 0.719196036042, 202), (25, 276, 0.72119258703, 212), (25, 276, 0.724848372617, 201),
(25, 276, 0.727773523116, 947132), (25, 276, 0.786181091729, 223), (25, 276, 0.835470024888, 213), (25, 276, 0.850785506884, 1650536293),
(25, 276, 0.872106280647, 205), (25, 277, 0.409025006548, 1245), (25, 277, 0.432733743192, 200), (25, 277, 0.571657665503, 45217),
(25, 277, 0.702562712047, 201), (25, 277, 0.730418085673, 575), (25, 277, 0.749515377892, 200), (25, 277, 0.775231917334, 200),
(25, 277, 0.790660296053, 204), (25, 277, 0.875858958177, 236), (25, 278, 0.379322394893, 309), (25, 278, 0.420790416182, 201),
(25, 278, 0.527244364126, 200), (25, 278, 0.615000956496, 205), (25, 278, 0.675667333791, 201), (25, 278, 0.696208960885, 201),
(25, 278, 0.790420764423, 204), (25, 278, 0.841240203947, 523), (25, 279, 0.341095083629, 201), (25, 279, 0.476230165726, 1798),
(25, 279, 0.518063098433, 209), (25, 279, 0.656454646158, 306), (25, 279, 0.684136349, 273), (25, 279, 0.709847569568, 119033),
(25, 279, 0.762133225185, 200), (25, 279, 0.776577127267, 200), (25, 279, 0.79611434817, 201), (25, 279, 0.808780479341, 425),
(25, 279, 0.850439803007, 204), (25, 279, 0.898230041029, 204), (25, 279, 0.945894882249, 616), (25, 280, 0.368073973138, 14001),
(25, 280, 0.464321107456, 1523), (25, 280, 0.617310083425, 504403), (25, 280, 0.657193497398, 204), (25, 280, 0.707839204221, 1265268),
(25, 280, 0.76379246649, 304), (25, 280, 0.772912128233, 201), (25, 280, 0.865579809939, 77454), (25, 281, 0.475947154647, 200),
(25, 281, 0.557771053261, 2188305), (25, 281, 0.56666775076, 12340), (25, 281, 0.638041977737, 200), (25, 281, 0.668510798451, 212),
(25, 281, 0.678366665681, 1294), (25, 281, 0.716116162808, 213), (25, 281, 0.748052894007, 203), (25, 281, 0.749911576065, 23865988060),
(25, 281, 0.759712569326, 204), (25, 281, 0.806434961546, 353082), (25, 281, 0.893617069228, 200), (25, 281, 0.931891968132, 203),
(25, 282, 0.454895506694, 11408), (25, 282, 0.549639923973, 462), (25, 282, 0.569017378489, 201), (25, 282, 0.577850694309, 200),
(25, 282, 0.584479523845, 334042071872), (25, 282, 0.599723920362, 200), (25, 282, 0.632612897763, 1293),
(25, 282, 0.681109488172, 200), (25, 282, 0.724133951717, 200), (25, 282, 0.754930901531, 201), (25, 282, 0.778740223985, 203),
(25, 282, 0.779781137188, 200), (25, 282, 0.781305596085, 202), (25, 282, 0.83569736595, 200), (25, 282, 0.850446466345, 1253),
(25, 282, 0.859549928516, 201), (25, 282, 0.871855706726, 200), (25, 283, 0.327637841131, 200), (25, 283, 0.404249604299, 201),
(25, 283, 0.561172940189, 200), (25, 283, 0.668083130397, 201), (25, 283, 0.678629207223, 203), (25, 283, 0.74122980107, 208),
(25, 283, 0.744679958097, 200), (25, 283, 0.760349422921, 203), (25, 283, 0.781697384113, 209), (25, 283, 0.784799938769, 202),
(25, 283, 0.789112337759, 236), (25, 283, 0.819466827649, 262), (25, 283, 0.839687812522, 200), (25, 283, 0.856859655325, 271),
(25, 284, 0.495523668627, 201), (25, 284, 0.56435102208, 205), (25, 284, 0.588093361148, 219), (25, 284, 0.593268824769, 200),
(25, 284, 0.640596228637, 213), (25, 284, 0.653491369691, 44714), (25, 284, 0.675009753521, 202), (25, 284, 0.773401673731, 200),
(25, 284, 0.805092875342, 213), (25, 284, 0.82735685621, 263), (25, 284, 0.840696528783, 16521), (25, 285, 0.362802762398, 320),
(25, 285, 0.367012291981, 20073), (25, 285, 0.521190733548, 200), (25, 285, 0.575799236698, 200), (25, 285, 0.637555604061, 201),
(25, 285, 0.642866106846, 200), (25, 285, 0.739442877608, 1154709), (25, 285, 0.740973872676, 205), (25, 285, 0.779312184025, 258),
(25, 285, 0.7798668215, 1286), (25, 285, 0.841286817662, 200), (25, 285, 0.913642856385, 858), (25, 286, 0.526160290087, 202),
(25, 286, 0.57102556171, 200), (25, 286, 0.605564882529, 200), (25, 286, 0.673079677685, 202), (25, 286, 0.675864181927, 200),
(25, 286, 0.723247596231, 224), (25, 286, 0.723347705484, 203), (25, 286, 0.767358570943, 207), (25, 286, 0.775537484183, 241),
(25, 286, 0.780033922166, 2962), (25, 286, 0.806301077907, 1553), (25, 286, 0.829016366841, 200), (25, 286, 0.839169441571, 200),
(25, 286, 0.852776222427, 28148), (25, 286, 0.853758532671, 200), (25, 286, 0.906829095884, 200), (25, 286, 0.922712587421, 202),
(25, 287, 0.498032911641, 200), (25, 287, 0.592863506249, 233), (25, 287, 0.622406587519, 208), (25, 287, 0.718903577193, 218),
(25, 287, 0.72138759488, 227), (25, 287, 0.749942677419, 240), (25, 287, 0.762366566525, 215), (25, 287, 0.770805576807, 200),
(25, 287, 0.797492731584, 200), (25, 287, 0.835165503936, 200), (25, 287, 0.946751084636, 863358347021),
(25, 288, 0.306016851261, 201), (25, 288, 0.468949036459, 4770), (25, 288, 0.549651576351, 201), (25, 288, 0.592965066535, 6236),
(25, 288, 0.706825000163, 216), (25, 288, 0.74286176604, 41482), (25, 288, 0.743238045326, 206), (25, 288, 0.777949156606, 213),
(25, 288, 0.781597068828, 418), (25, 288, 0.794578713285, 200), (25, 288, 0.828331653519, 418), (25, 288, 0.834874015356, 212),
(25, 288, 0.848009292304, 200), (25, 288, 0.852116433152, 200), (25, 288, 0.906593204881, 202), (25, 288, 0.920623087617, 220),
(25, 289, 0.524452337599, 1057), (25, 289, 0.552951317234, 208), (25, 289, 0.651146664053, 200), (25, 289, 0.658611767347, 1126709768047),
(25, 289, 0.691072913786, 201), (25, 289, 0.695521738775, 42204), (25, 289, 0.710204540486, 207), (25, 289, 0.716186135845, 3696),
(25, 289, 0.748287169753, 209), (25, 289, 0.750374480604, 201), (25, 289, 0.810573219838, 201), (25, 289, 0.824662154794, 200),
(25, 289, 0.881953772318, 200), (25, 289, 0.885424313568, 200), (25, 290, 0.478371525842, 2087), (25, 290, 0.509245836087, 200),
(25, 290, 0.559208272006, 202), (25, 290, 0.566118076472, 336), (25, 290, 0.592660738469, 200), (25, 290, 0.594018239861, 273),
(25, 290, 0.609100591562, 201), (25, 290, 0.613710234154, 235), (25, 290, 0.622454795175, 201), (25, 290, 0.642187814474, 201),
(25, 290, 0.650179222226, 202), (25, 290, 0.71534164315, 3261), (25, 290, 0.720180673012, 206), (25, 290, 0.737585832942, 200),
(25, 290, 0.775169473922, 229), (25, 290, 0.783784198305, 53137), (25, 290, 0.789135961744, 201), (25, 290, 0.800078889184, 200),
(25, 291, 0.405626786206, 34744), (25, 291, 0.525738841457, 211), (25, 291, 0.533871294974, 12996), (25, 291, 0.608310459901, 201),
(25, 291, 0.70893418817, 200), (25, 291, 0.748805670518, 200), (25, 291, 0.760314517315, 202), (25, 291, 0.760919201657, 215),
(25, 291, 0.763324684293, 200), (25, 291, 0.778634985402, 200), (25, 291, 0.805883746215, 200), (25, 291, 0.827079825705, 203),
(25, 291, 0.827672243803, 200), (25, 292, 0.353361504401, 9552), (25, 292, 0.413680391502, 240), (25, 292, 0.498283007005, 200),
(25, 292, 0.560682661174, 201), (25, 292, 0.660502227784, 201), (25, 292, 0.676014312494, 200), (25, 292, 0.729161823418, 200),
(25, 292, 0.754733824112, 230), (25, 292, 0.772617271317, 312), (25, 292, 0.778956063712, 212), (25, 292, 0.808767644485, 200),
(25, 292, 0.808779697891, 201), (25, 292, 0.844087667679, 202), (25, 292, 0.904903907681, 200), (25, 293, 0.524954771554, 4945),
(25, 293, 0.57444832542, 233), (25, 293, 0.600122035306, 200), (25, 293, 0.69001246376, 205), (25, 293, 0.691232039332, 207),
(25, 293, 0.691742268177, 211), (25, 293, 0.698366150359, 200), (25, 293, 0.711927031055, 1815880), (25, 293, 0.71619667357, 3964),
(25, 293, 0.728536730678, 200), (25, 293, 0.741604172773, 200), (25, 293, 0.743399425593, 201), (25, 293, 0.758084864431, 200),
(25, 293, 0.759978441853, 200), (25, 293, 0.780081691192, 1448778253), (25, 293, 0.788319084437, 208),
(25, 293, 0.801525808156, 200), (25, 293, 0.813155425067, 206), (25, 293, 0.819811779201, 377), (25, 293, 0.837649946204, 209),
(25, 293, 0.869752644338, 4592), (25, 293, 0.875398670372, 200), (25, 293, 0.918150841685, 200), (25, 293, 0.921450726956, 201),
(25, 294, 0.445036622233, 202), (25, 294, 0.496380029754, 2294499), (25, 294, 0.517533203971, 214), (25, 294, 0.597738939234, 213),
(25, 294, 0.597783619419, 102427), (25, 294, 0.600782734524, 263), (25, 294, 0.625741320644, 200), (25, 294, 0.632555212361, 202),
(25, 294, 0.633928301179, 217), (25, 294, 0.720710116312, 200), (25, 294, 0.741687972492, 235), (25, 294, 0.775184150825, 203),
(25, 294, 0.799975478422, 2129), (25, 294, 0.811533351383, 221), (25, 294, 0.827766846665, 47518), (25, 294, 0.834896019626, 200),
(25, 294, 0.855889683449, 200), (25, 294, 0.887096214635, 201), (25, 294, 0.898185143854, 200), (25, 294, 0.904470557778, 207),
(25, 295, 0.510000548384, 4948), (25, 295, 0.527335029277, 48990), (25, 295, 0.553592976478, 200), (25, 295, 0.587128450848, 200),
(25, 295, 0.685163151117, 221), (25, 295, 0.689665955815, 200), (25, 295, 0.693619741737, 200), (25, 295, 0.698808800461, 212),
(25, 295, 0.79024052726, 203), (25, 295, 0.805930533305, 233), (25, 295, 0.870408868052, 208), (25, 295, 0.879989559956, 209),
(25, 295, 0.917289124506, 201), (25, 296, 0.368675367618, 200), (25, 296, 0.422106669815, 87196), (25, 296, 0.570294648439, 201),
(25, 296, 0.576307309235, 5064), (25, 296, 0.577913079103, 223), (25, 296, 0.615569633698, 201), (25, 296, 0.619178871735, 43506),
(25, 296, 0.718168554371, 310), (25, 296, 0.747322660094, 202), (25, 296, 0.760729108487, 200), (25, 296, 0.822530768331, 205),
(25, 296, 0.836178694446, 200), (25, 296, 0.922082501039, 202), (25, 297, 0.575427625651, 325), (25, 297, 0.582330676039, 200),
(25, 297, 0.59032029128, 201), (25, 297, 0.590800056359, 200), (25, 297, 0.601983239354, 200), (25, 297, 0.604624445572, 349),
(25, 297, 0.618592598637, 275), (25, 297, 0.630430484034, 1804), (25, 297, 0.747994935933, 200), (25, 297, 0.761287220637, 201),
(25, 297, 0.784311762717, 24040), (25, 297, 0.805896793235, 207), (25, 297, 0.83131315563, 213), (25, 297, 0.859395579848, 209),
(25, 297, 0.878201883463, 201), (25, 298, 0.365915091546, 7657), (25, 298, 0.52132925192, 201), (25, 298, 0.615089219457, 212),
(25, 298, 0.637405757267, 200), (25, 298, 0.688423448322, 214), (25, 298, 0.745560344488, 206), (25, 298, 0.80183307542, 589),
(25, 298, 0.870426520049, 272), (25, 298, 0.89547470974, 623), (25, 299, 0.439413983287, 621), (25, 299, 0.635744201316, 400665320),
(25, 299, 0.635839800048, 203), (25, 299, 0.654855825396, 230), (25, 299, 0.663358277149, 200), (25, 299, 0.716539473345, 206),
(25, 299, 0.720916562601, 201), (25, 299, 0.751504283345, 239), (25, 299, 0.757182123011, 201), (25, 299, 0.783947882789, 34957848),
(25, 299, 0.787635290729, 2549771968), (25, 299, 0.810452875242, 200), (25, 299, 0.817501090944, 200),
(25, 299, 0.825030647643, 202), (25, 299, 0.826381476756, 201309), (25, 299, 0.827561766471, 200), (25, 299, 0.838546065913, 406),
(25, 299, 0.838668086492, 41065010), (25, 299, 0.849677138359, 205), (25, 299, 0.888747407578, 203), (25, 300, 0.409478159695, 204),
(25, 300, 0.422098065762, 127064), (25, 300, 0.461635641331, 215), (25, 300, 0.509929449334, 200), (25, 300, 0.526075686173, 249),
(25, 300, 0.570498723667, 200), (25, 300, 0.608851280889, 104165306), (25, 300, 0.63030529901, 200), (25, 300, 0.672317987371, 664),
(25, 300, 0.673406231884, 200), (25, 300, 0.680327735756, 3147), (25, 300, 0.69178511648, 482), (25, 300, 0.72755905432, 201),
(25, 300, 0.732997721442, 212), (25, 300, 0.753568752527, 200), (25, 300, 0.772028272907, 202), (25, 300, 0.779901373004, 21845295),
(25, 300, 0.787993478282, 812414), (25, 300, 0.803550492942, 206), (25, 300, 0.874415087757, 263), (25, 300, 0.885236357353, 331970),
(25, 300, 0.894826991604, 588), (25, 300, 0.902637609898, 85410), (25, 301, 0.360093850862, 204), (25, 301, 0.400165301316, 201),
(25, 301, 0.469204018151, 200), (25, 301, 0.537073638156, 200), (25, 301, 0.546705498921, 203), (25, 301, 0.592970028946, 303),
(25, 301, 0.608415628183, 200), (25, 301, 0.63288933406, 2859), (25, 301, 0.63664042403, 970), (25, 301, 0.64529111355, 402),
(25, 301, 0.681233825938, 200), (25, 301, 0.690899753273, 210), (25, 301, 0.692879776665, 200), (25, 301, 0.748166942643, 201),
(25, 301, 0.780381651924, 201), (25, 301, 0.786615600294, 240), (25, 301, 0.796162957093, 218), (25, 301, 0.814111079911, 200),
(25, 301, 0.829147987825, 200), (25, 301, 0.842615885711, 226), (25, 301, 0.848517486075, 54928), (25, 301, 0.89833095029, 1550),
(25, 302, 0.405983475031, 18159), (25, 302, 0.584932652676, 220), (25, 302, 0.64638274985, 200), (25, 302, 0.704969570047, 201),
(25, 302, 0.706051626625, 200), (25, 302, 0.741692298627, 201), (25, 302, 0.756403039924, 236), (25, 302, 0.775208821424, 205),
(25, 302, 0.820549125721, 6413), (25, 302, 0.843449911907, 202), (25, 302, 0.854836903637, 1444), (25, 302, 0.959731993346, 18110751),
(25, 303, 0.424498218556, 202), (25, 303, 0.59564207646, 5859), (25, 303, 0.628957916397, 312), (25, 303, 0.675945884436, 405),
(25, 303, 0.703924077074, 3436122), (25, 303, 0.775340096428, 203), (25, 303, 0.840799001056, 200), (25, 303, 0.843478387795, 200),
(25, 303, 0.843620594265, 201), (25, 303, 0.882905827794, 200), (25, 303, 0.891407840196, 201), (25, 303, 0.928661184425, 200),
(25, 304, 0.612209498336, 200), (25, 304, 0.632934680031, 217), (25, 304, 0.680037492863, 208), (25, 304, 0.702135166708, 201),
(25, 304, 0.739443325164, 200), (25, 304, 0.792856089945, 18219), (25, 304, 0.793868715939, 1195), (25, 304, 0.807936872595, 243),
(25, 304, 0.855967740382, 9139), (25, 304, 0.876774098031, 264), (25, 304, 0.908151496191, 200), (25, 304, 0.909811696417, 201),
(25, 305, 0.467412185835, 220), (25, 305, 0.504357824329, 202), (25, 305, 0.551514171063, 1813205), (25, 305, 0.562075541816, 28957),
(25, 305, 0.565839799799, 200), (25, 305, 0.57478857299, 201), (25, 305, 0.616735566246, 18968), (25, 305, 0.694741607886, 211),
(25, 305, 0.730098365549, 350), (25, 305, 0.74553240102, 3669), (25, 305, 0.775373331324, 273), (25, 305, 0.782999134264, 202),
(25, 305, 0.8326463963, 1718174), (25, 305, 0.84309553266, 34103), (25, 305, 0.853174396025, 202), (25, 305, 0.866990268211, 200),
(25, 305, 0.95814576074, 207), (25, 306, 0.426358484538, 2619), (25, 306, 0.601491940798, 1236), (25, 306, 0.656076249659, 201),
(25, 306, 0.667159358364, 8851), (25, 306, 0.680137137507, 93771), (25, 306, 0.702048987783, 215), (25, 306, 0.736768186781, 200),
(25, 306, 0.766656078382, 225), (25, 306, 0.778572773772, 201), (25, 306, 0.788035864564, 224), (25, 306, 0.810667703089, 203),
(25, 306, 0.816630755616, 10977626), (25, 306, 0.874526902796, 207), (25, 306, 0.909874167041, 200), (25, 306, 0.937873115764, 201),
(25, 307, 0.399427943647, 308), (25, 307, 0.502741334176, 210), (25, 307, 0.529663281186, 1180), (25, 307, 0.630224185157, 200),
(25, 307, 0.632031271401, 218), (25, 307, 0.640704995246, 203), (25, 307, 0.69831193803, 77936), (25, 307, 0.702814625747, 201),
(25, 307, 0.747406138489, 202), (25, 307, 0.747958417038, 204), (25, 307, 0.784937576368, 1648), (25, 307, 0.794869553561, 201),
(25, 307, 0.828787292708, 9683), (25, 307, 0.863132135591, 207), (25, 307, 0.869668447709, 207), (25, 307, 0.871174430814, 1874),
(25, 307, 0.874024275077, 210), (25, 307, 0.888454459822, 2205), (25, 307, 0.908595383436, 1066), (25, 308, 0.325783846322, 203),
(25, 308, 0.397224619923, 201), (25, 308, 0.398632358505, 1866), (25, 308, 0.549245225571, 223), (25, 308, 0.614176736202, 1627),
(25, 308, 0.657868307531, 835565), (25, 308, 0.720171327788, 102155), (25, 308, 0.760576054602, 202), (25, 308, 0.789153275477, 205),
(25, 308, 0.923998732287, 201), (25, 309, 0.561546536824, 200), (25, 309, 0.635434397698, 200), (25, 309, 0.643406617116, 203),
(25, 309, 0.658560572878, 200), (25, 309, 0.674697791801, 248), (25, 309, 0.676725636526, 228), (25, 309, 0.676937775159, 200),
(25, 309, 0.6792495829, 221), (25, 309, 0.716486921989, 200), (25, 309, 0.725512876373, 78653), (25, 309, 0.757976245878, 746),
(25, 309, 0.781027844906, 200), (25, 309, 0.78623950218, 257), (25, 309, 0.810962413638, 230), (25, 310, 0.260183128022, 4099),
(25, 310, 0.587394172232, 251), (25, 310, 0.621739526011, 322), (25, 310, 0.64027318687, 204), (25, 310, 0.67688167552, 202),
(25, 310, 0.683476431144, 203), (25, 310, 0.74431135893, 10529), (25, 310, 0.804336362739, 201), (25, 310, 0.809925171125, 224),
(25, 310, 0.84167604034, 219), (25, 310, 0.914653852136, 240), (25, 311, 0.312014901261, 200), (25, 311, 0.565120276608, 1451),
(25, 311, 0.668447484328, 200), (25, 311, 0.693205380973, 201), (25, 311, 0.715572448621, 200), (25, 311, 0.735871833159, 206),
(25, 311, 0.754197545032, 201), (25, 311, 0.755255511596, 207), (25, 311, 0.797893642622, 200), (25, 311, 0.82548808715, 629357488),
(25, 311, 0.848601310255, 212), (25, 311, 0.893160345087, 222), (25, 311, 0.907535669966, 210), (25, 312, 0.390384390913, 223),
(25, 312, 0.404305090449, 201), (25, 312, 0.587382901527, 200), (25, 312, 0.607534113237, 204), (25, 312, 0.719561090933, 2427),
(25, 312, 0.765116208912, 207), (25, 312, 0.768884636481, 201), (25, 312, 0.77321985892, 136853), (25, 312, 0.781591538183, 357),
(25, 312, 0.786119097558, 3483946), (25, 312, 0.848619555391, 11017), (25, 312, 0.954299904225, 200), (25, 312, 0.955187319821, 204),
(25, 313, 0.529251017792, 204), (25, 313, 0.541364870877, 200), (25, 313, 0.60546139467, 230), (25, 313, 0.61482220499, 24877),
(25, 313, 0.638663284904, 209), (25, 313, 0.644164848762, 200), (25, 313, 0.64713451255, 200), (25, 313, 0.743586331391, 201),
(25, 313, 0.775805821428, 62845), (25, 313, 0.798122759695, 7977), (25, 313, 0.858577862803, 127038), (25, 313, 0.866823531593, 200),
(25, 313, 0.876882672035, 283), (25, 313, 0.917675334467, 200), (25, 314, 0.369362271547, 200), (25, 314, 0.37571281143, 7538438),
(25, 314, 0.421702878008, 872), (25, 314, 0.512143047288, 200), (25, 314, 0.615334964732, 41957), (25, 314, 0.634135010466, 201),
(25, 314, 0.65143589365, 5976), (25, 314, 0.6624335318, 202), (25, 314, 0.687439523632, 207), (25, 314, 0.70341643248, 219100),
(25, 314, 0.71373952253, 200), (25, 314, 0.716799246311, 200), (25, 314, 0.736070231117, 202), (25, 314, 0.769820801936, 201),
(25, 314, 0.796382966462, 1810920), (25, 314, 0.817248231272, 200), (25, 314, 0.911372340659, 217771),
(25, 315, 0.494168494957, 200), (25, 315, 0.525928344185, 108504), (25, 315, 0.530891192429, 309), (25, 315, 0.543427134741, 570),
(25, 315, 0.582642352511, 200), (25, 315, 0.62020198716, 204), (25, 315, 0.66021096512, 201), (25, 315, 0.810810141201, 125205306),
(25, 315, 0.875437215808, 201), (25, 315, 0.891388896727, 202), (25, 315, 0.950706326773, 230), (25, 316, 0.531487130493, 203),
(25, 316, 0.618472935292, 251), (25, 316, 0.647254887133, 206), (25, 316, 0.653924814146, 212), (25, 316, 0.667901497546, 212),
(25, 316, 0.708180220581, 200), (25, 316, 0.760548015821, 2030), (25, 316, 0.768690555637, 200), (25, 316, 0.774476148446, 200),
(25, 316, 0.796262761253, 201), (25, 316, 0.796625765733, 200), (25, 316, 0.823221552247, 200), (25, 316, 0.830702399623, 200),
(25, 316, 0.836360274124, 325), (25, 316, 0.896613527206, 248), (25, 317, 0.482186115357, 383), (25, 317, 0.576756996375, 200),
(25, 317, 0.578057886341, 204), (25, 317, 0.594056991632, 203), (25, 317, 0.631811741834, 200), (25, 317, 0.634065817187, 201),
(25, 317, 0.738259051865, 200), (25, 317, 0.741522939153, 200), (25, 317, 0.753479524136, 2637045), (25, 317, 0.776711507455, 301),
(25, 317, 0.788723637838, 222), (25, 317, 0.859905403917, 201), (25, 318, 0.524837076185, 783), (25, 318, 0.570833052501, 324),
(25, 318, 0.578522088699, 201), (25, 318, 0.657902296334, 202), (25, 318, 0.677142738648, 200), (25, 318, 0.726613137498, 769),
(25, 318, 0.732167007028, 209), (25, 318, 0.774227686638, 371), (25, 318, 0.827201651993, 202), (25, 318, 0.847552472266, 333),
(25, 319, 0.299119763862, 203), (25, 319, 0.45927498818, 201), (25, 319, 0.516148758591, 203), (25, 319, 0.615909131871, 4852),
(25, 319, 0.632155319322, 108442), (25, 319, 0.646735509589, 260), (25, 319, 0.650284817404, 205), (25, 319, 0.686381662086, 9214),
(25, 319, 0.693039056628, 200), (25, 319, 0.744051833919, 202), (25, 319, 0.766865749349, 200), (25, 319, 0.787624751367, 209),
(25, 319, 0.80385182439, 201), (25, 319, 0.828506576415, 203), (25, 319, 0.882672117998, 236), (25, 319, 0.897596538512, 320),
(25, 320, 0.463229776045, 201), (25, 320, 0.495664364554, 543), (25, 320, 0.557110073697, 46084), (25, 320, 0.564003442697, 228),
(25, 320, 0.592427293085, 200), (25, 320, 0.647193255894, 541), (25, 320, 0.687780061052, 305), (25, 320, 0.804990051837, 204),
(25, 320, 0.812916984869, 1331), (25, 320, 0.931548693535, 1716800), (25, 321, 0.629165408494, 202), (25, 321, 0.646414688214, 1085812),
(25, 321, 0.675364980195, 20790), (25, 321, 0.681600225983, 206), (25, 321, 0.685460441866, 13703), (25, 321, 0.832202070011, 236),
(25, 321, 0.869702143767, 228), (25, 322, 0.359393286821, 200), (25, 322, 0.456060077056, 234), (25, 322, 0.489952848972, 219),
(25, 322, 0.514488904665, 327), (25, 322, 0.599151587589, 200), (25, 322, 0.669303689783, 200), (25, 322, 0.696930419223, 216),
(25, 322, 0.727835215524, 477), (25, 322, 0.80782526029, 200), (25, 322, 0.833256121648, 129263), (25, 322, 0.870336001756, 216),
(25, 322, 0.940963125417, 679), (25, 323, 0.396053762877, 201), (25, 323, 0.425459758563, 200), (25, 323, 0.55251719767, 201),
(25, 323, 0.584884865708, 200), (25, 323, 0.609829616479, 203), (25, 323, 0.612493852048, 322), (25, 323, 0.691710173338, 201),
(25, 323, 0.71108498005, 311), (25, 323, 0.788507519521, 203), (25, 323, 0.807011603621, 200), (25, 323, 0.828169583641, 201),
(25, 323, 0.913928205211, 201), (25, 324, 0.45836160144, 200), (25, 324, 0.499107021276, 13215), (25, 324, 0.559870976212, 200),
(25, 324, 0.603511924685, 200), (25, 324, 0.623198421134, 210), (25, 324, 0.633639995522, 338), (25, 324, 0.635556007837, 246),
(25, 324, 0.683944057834, 364), (25, 324, 0.730240665978, 202), (25, 324, 0.786380149202, 859), (25, 324, 0.798736866984, 263),
(25, 324, 0.805943711046, 298), (25, 324, 0.820587885957, 201), (25, 325, 0.231831459255, 200), (25, 325, 0.563362833248, 239),
(25, 325, 0.636026944883, 21971), (25, 325, 0.669608327745, 200), (25, 325, 0.716574236797, 200), (25, 325, 0.724404665933, 206),
(25, 325, 0.739644789795, 40472), (25, 325, 0.752542864573, 200), (25, 325, 0.824388257792, 6198), (25, 325, 0.915197856113, 202),
(25, 326, 0.707329416062, 208), (25, 326, 0.728563259999, 204), (25, 326, 0.752738034251, 201), (25, 326, 0.825564275897, 204),
(25, 327, 0.719013790228, 203), (25, 327, 0.72228899991, 200), (25, 327, 0.751466201033, 209), (25, 327, 0.759232117888, 211),
(25, 327, 0.767027224929, 1537), (25, 327, 0.778548686629, 203), (25, 327, 0.784075647798, 200), (25, 327, 0.793621518891, 200),
(25, 327, 0.806195524296, 229), (25, 327, 0.808608560267, 201), (25, 327, 0.827857910169, 572), (25, 328, 0.393098272591, 203),
(25, 328, 0.394325016086, 2993), (25, 328, 0.56951420425, 201), (25, 328, 0.580323359062, 2924475), (25, 328, 0.580905747982, 201),
(25, 328, 0.583192577095, 542), (25, 328, 0.597499239304, 213), (25, 328, 0.600613025852, 253), (25, 328, 0.621643431237, 436),
(25, 328, 0.701710063929, 200), (25, 328, 0.716681957271, 202), (25, 328, 0.761650010569, 202), (25, 328, 0.772259027715, 206),
(25, 328, 0.779616327067, 200), (25, 328, 0.866568305949, 201), (25, 328, 0.898210193557, 515), (25, 329, 0.375129736945, 211),
(25, 329, 0.446336810237, 285), (25, 329, 0.642038213561, 1496), (25, 329, 0.645488070638, 205), (25, 329, 0.771011371351, 203),
(25, 329, 0.829964202191, 212), (25, 330, 0.511762908051, 201), (25, 330, 0.518705307319, 200), (25, 330, 0.584850797881, 200),
(25, 330, 0.730246394391, 135696), (25, 330, 0.751681569544, 2366819428908), (25, 330, 0.92157485973, 200),
(25, 331, 0.393252838456, 201), (25, 331, 0.413705536186, 200), (25, 331, 0.541667450199, 200), (25, 331, 0.610163703725, 202),
(25, 331, 0.662097234233, 201), (25, 331, 0.711996875688, 557), (25, 331, 0.756070937233, 200), (25, 331, 0.77482801802, 660),
(25, 331, 0.785152716014, 202), (25, 331, 0.804310562109, 201), (25, 331, 0.869247778778, 202), (25, 331, 0.900011576777, 206),
(25, 332, 0.360501981662, 200), (25, 332, 0.396119173231, 1350), (25, 332, 0.549423865109, 204), (25, 332, 0.572660049768, 12648),
(25, 332, 0.626922110118, 200), (25, 332, 0.725028858444, 7829535), (25, 332, 0.770714243024, 200), (25, 332, 0.778895975847, 228),
(25, 332, 0.790939903651, 200), (25, 332, 0.845479439223, 204), (25, 333, 0.552595567924, 4737), (25, 333, 0.628912424024, 230),
(25, 333, 0.712025685826, 205), (25, 333, 0.745406810596, 201), (25, 333, 0.905976663231, 205), (25, 334, 0.483908768827, 207),
(25, 334, 0.60959982508, 200), (25, 334, 0.812519911253, 224), (25, 334, 0.843221977913, 217), (25, 335, 0.60973667496, 201),
(25, 335, 0.693600650693, 201), (25, 335, 0.728238441845, 203), (25, 335, 0.75743368108, 210), (25, 335, 0.810360530954, 207),
(25, 335, 0.882951536209, 200), (25, 335, 0.893759028105, 208), (25, 336, 0.740623773204, 201), (25, 336, 0.755244695771, 204),
(25, 336, 0.831100589453, 200), (25, 337, 0.703493435921, 327), (25, 337, 0.718881873842, 226), (25, 337, 0.81048243721, 206),
(25, 337, 0.899330103434, 18637), (25, 338, 0.700633185403, 206), (25, 338, 0.802867938789, 205), (25, 338, 0.805246709953, 4733064),
(25, 338, 0.861528612477, 217), (25, 338, 0.875310494507, 201), (25, 339, 0.530202056325, 201), (25, 339, 0.596821460467, 206),
(25, 339, 0.637622807415, 201), (25, 339, 0.720319384906, 1063), (25, 339, 0.925562964099, 241), (25, 340, 0.545836200959, 81897),
(25, 340, 0.575462739406, 8298), (25, 340, 0.66454554903, 392), (25, 340, 0.665110271015, 200), (25, 340, 0.682396835586, 583),
(25, 340, 0.705902758344, 216), (25, 341, 0.485770196306, 202), (25, 341, 0.572928076121, 8075702), (25, 341, 0.584378279664, 200),
(25, 341, 0.671131495684, 201), (25, 341, 0.681341791186, 255), (25, 341, 0.729285274999, 56404734), (25, 341, 0.817259802301, 214),
(25, 342, 0.7941751354, 201), (25, 342, 0.815001400116, 209), (25, 343, 0.713674285547, 204), (25, 343, 0.776290208985, 210),
(25, 344, 0.578809632483, 200), (25, 344, 0.602669599066, 204), (25, 344, 0.640884720483, 201), (25, 344, 0.689617532849, 200),
(25, 344, 0.735474986847, 793226), (25, 344, 0.801550588878, 200), (25, 345, 0.511613953266, 200), (25, 345, 0.599632141615, 3606),
(25, 345, 0.725633060098, 213), (25, 345, 0.864442340693, 200), (25, 346, 0.629039256263, 519), (25, 346, 0.868847037952, 26139957),
(25, 347, 0.383146657028, 505762), (25, 347, 0.793122392817, 887), (25, 348, 0.634239706868, 200), (25, 348, 0.747883842713, 908),
(25, 348, 0.751757880877, 206), (25, 349, 0.617658321678, 200), (25, 350, 0.747783531486, 2330), (25, 350, 0.860911393971, 338),
(25, 352, 0.686825990299, 10332), (25, 353, 0.683483882694, 227), (25, 353, 0.693201365913, 201), (25, 353, 0.86051685785, 79018),
(25, 354, 0.700525525741, 200), (25, 355, 0.81145294361, 2178), (25, 356, 0.595846869158, 200), (25, 356, 0.619201382241, 1819),
(25, 358, 0.563881791069, 210), (25, 358, 0.69894141965, 200), (25, 358, 0.743018024778, 325), (25, 358, 0.797592813469, 200),
(25, 360, 0.663337283569, 258), (25, 360, 0.788791573196, 376), (25, 361, 0.527838758249, 290), (25, 361, 0.64267249425, 242),
(25, 363, 0.487136757184, 200), (25, 365, 0.734633994789, 213), (25, 365, 0.889239450729, 225), (25, 368, 0.664001959486, 201),
(25, 370, 0.593215752818, 1180660)]Lower Bound
One baseline would be to simply take our pre-existing exact solution V/VPplan and run it on the generalized Kelly by ignoring observations and assuming 300 rounds. It will probably perform reasonably well since it performs optimally at least one possible setting, and serve as a baseline:
import gym
env = gym.make('KellyCoinflipGeneralized-v0')
rewards = []
for n in range(0,1000):
done = False
reward = 0
roundsLeft = 300
while not done:
w = env._get_obs()[0][0]
b = roundsLeft
bet = VPplan(w, b)
results = env._step(bet*100)
reward = reward+results[1]
print n, w, b, bet, "results:", results
roundsLeft = max(0, roundsLeft - 1)
done = results[2]
rewards.append(reward)
env._reset()
print sum(rewards)/len(rewards)
# 140.642807947In the general game, it performs poorly because it self-limits to $250 in the many games where the max cap is higher, and it often wipes out to $0 in games where the edge is small or negative.
Deep RL
Since the Bayesian decision tree is too hard to compute in full, we need a different approach. Tabular approaches in general will have difficulty as the full history makes the state-space vastly larger, but also so do just the sufficient statistics of wins/losses + rounds elapsed + maximum observed wealth.
One approach which should be able to cope with the complexities would be deep reinforcement learning, whose neural networks let them optimize well in difficult environments, and given the sufficient statistics, we don’t need to train an explicitly Bayesian agent, as a deep RL agent trained on random instances can learn a reactive policy which adapts ‘online’ and computes an approximation of the Bayes-optimal agent ( et al 2019 is a good review of DRL/Bayesian RL), which as we have already seen is intractable even for small problems like this.
Unfortunately, the sparsity of rewards in the Kelly coinflip game (receiving a reward only every ~300 steps) does make solving the game much harder for DRL agents.
To create a deep RL agent for the generalized Kelly coin-flip game, I will use the keras-rl library of agents, which is based on the Keras deep learning framework (backed by TensorFlow); deep learning is often sensitive to choice of hyperparameters, so for hyperparameter optimization, I use the hyperas wrapper around hyperopt (paper).
keras-rl offers primarily3 DQN ( et al 2013) and DDPG ( et al 2015).
DQN is a possibility but for efficiency4 most DQN implementations require/assume a fixed number of actions, which in our case of penny-level betting, implies having 25,000 distinct unordered actions. I tried prototyping DQN for the simple Kelly coin-flip game using the keras-rl DQN example (Cartpole), but after hours, it still had not received any rewards—it repeatedly bet more than its current wealth, equivalent to its current wealth, and busting out, never managing to go 300 rounds to receive any reward and begin learning. (This sort of issue with sparse rewards is a common problem with DQN and deep RL in general, as the most common forms of exploration will flail around at random rather than make deep targeted exploration of particular strategies or try to seek out new regions of state-space which might contain rewards.) One possibility would have been to ‘cheat’ by using the exact value function to provide optimal trajectories for the DQN agent to learn from.
DDPG isn’t like tabular learning but is a policy gradient method (Karpathy explains policy gradients). With deep policy gradients, the basic idea is that the ‘actor’ NN repeatedly outputs an action based on the current state, and then at the end of the episode with the final total reward, if the reward is higher than expected, all the neurons who contributed to all the actions get strengthened to be more likely to produce those actions, and if the reward is lower than expected, they are weakened. This is a very indiscriminate error-filled way to train neurons, but it does work if run over enough episodes for the errors to cancel out; the noise can be reduced by training an additional ‘critic’ NN to predict the rewards from actions, based on an experience replay buffer. The NNs are usually fairly small (to avoid overfitting & because of the weak supervision), use RELUs, and the actor NN often has batchnorm added to it. (To prevent them from learning too fast and interfering with each other, a copy is made of each called the ‘target networks’.) For exploration, some random noise is added to the final action; not epsilon-random noise (like in DQN) but a sort of random walk, to make the continuous action consistently lower or higher (and avoid canceling out).
A continuous action would have less of an unordered action/curse of dimensionality required switching from DQN to DDPG (example). Unfortunately, DDPG also had initialization problems in overbetting, as its chosen actions would quickly drift to always betting either very large positive or negative numbers, which get converted to betting everything or $0 respectively (which then always result in no rewards via either busting & getting 0 or going 300 rounds & receiving a reward of 0), and it would never return to meaningful bets. To deal with the drift/busting out problem, I decided to add some sort of constraint on the agent: make it choose a continuous action 0–1 (squashed by a final sigmoid activation rather than linear or tanh), and convert it into a valid bet, so all bets would be meaningful and it would have less of a chance to overbet and bust out immediately. (This trick might also be usable in DQN if we discretize 0–1 into, say, 100 percentiles.) My knowledge of Keras is weak, so I was unsure how to convert an action 0–1 to a fraction of the agent’s current wealth, although I did figure out how to multiply it by $250 before passing it in. This resulted in meaningful progress but was sensitive to hyperparameters—for example, the DDPG appeared to train worse with a very large experience replay buffer than with the et al 2015 setting of 10,000.
Hyperparameter-wise, et al 2015 used, for the low-dimensional (non-ALE screen) RL problems similar to the general Kelly coin-flip, the settings:
2 hidden layers of 400 & 300 RELU neurons into a final tanh
an experience replay buffer of 10,000
Adam SGD optimization algorithm with learning rate: 10-4
discount/gamma: 0.99
minibatch size: 64
an Ornstein-Uhlenbeck process random walk, μ = 0, σ = 0.2, θ = 0.15.
For the simple Kelly coin-flip problem, the previous experiment with training based on the exact value function demonstrates that 400+300 neurons would be overkill, and probably a much smaller 3-layer network with <128 neurons would be more than adequate; the discount/gamma being set to 0.99 for Kelly is questionable, as almost no steps result in a reward, and a discount rate of 0.99 would imply for a 300 round game that the final reward from the perspective of the first round would be almost worthless (since 0.99300 = 0.049), so a discount rate of 0.999 or even just 1 would make more sense; because the reward is delayed, I expect the gradients to not be so helpful, and perhaps a lower learning rate or larger minibatch size would be required; finally, the exploration noise is probably too small, as the random walk would tend to increase or decrease bet amounts by less than $1, so probably a larger σ would be better. With these settings, DDPG can achieve an average per-step/round reward of ~0.8 as compared to the optimal average reward of 0.82 ($246 over 300 steps/rounds).
For the general Kelly coin-flip problem, the optimal average reward is unknown, but initial tries get ~0.7 (~$210). To try to discover better performance, I set up hyperparameter optimization using hyperas/hyperopt over the following parameters:
number of neurons in each layer in the actor and critic (16–128)
size of the experience replay buffer (0–100000)
exploration noise:
μ (𝒩(0,5))
θ (0–1)
σ (𝒩(3,3))
learning rate:
Adam, main NNs (log uniform −7 to −2; roughly, 0.14—0.00…)
Adam, target NNs (*)
minibatch size (8–2056)
Each agent/sample is trained ~8h and is evaluated on mean total reward over 200026ya episodes, with 120 samples total.
Full source code for the generalized Kelly coin-flip game DDPG:
import numpy as np
import gym
from hyperas.distributions import choice, randint, uniform, normal, loguniform
from hyperas import optim
from hyperopt import Trials, STATUS_OK, tpe
from keras.models import Sequential, Model
from keras.layers import Dense, Activation, Flatten, Input, concatenate, Lambda, BatchNormalization
from keras.optimizers import Adam
from rl.agents import DDPGAgent
from rl.memory import SequentialMemory
from rl.random import OrnsteinUhlenbeckProcess
def model(x_train, y_train, x_test, y_test):
ENV_NAME = 'KellyCoinflipGeneralized-v0'
gym.undo_logger_setup()
# Get the environment and extract the number of actions.
env = gym.make(ENV_NAME)
numpy.random.seed(123)
env.seed(123)
nb_actions = 1
# Next, we build a very simple model.
actor = Sequential()
actor.add(Flatten(input_shape=(1,) + (5,)))
actor.add(Dense({{choice([16, 32, 64, 96, 128])}}))
actor.add(BatchNormalization())
actor.add(Activation('relu'))
actor.add(Dense({{choice([16, 32, 64, 96, 128])}}))
actor.add(BatchNormalization())
actor.add(Activation('relu'))
actor.add(Dense({{choice([16, 32, 64, 96, 128])}}))
actor.add(BatchNormalization())
actor.add(Activation('relu'))
# pass into a single sigmoid to force a choice 0-1, corresponding to fraction of total possible wealth.
# It would be better to multiply the fraction against one's *current* wealth to reduce the pseudo-shift
# in optimal action with increasing wealth, but how do we set up a multiplication against the first
# original input in the Flatten layer? This apparently can't be done as a Sequential...
actor.add(Dense(nb_actions))
actor.add(BatchNormalization())
actor.add(Activation('sigmoid'))
actor.add(Lambda(lambda x: x*250))
print(actor.summary())
action_input = Input(shape=(nb_actions,), name='action_input')
observation_input = Input(shape=(1,) + (5,), name='observation_input')
flattened_observation = Flatten()(observation_input)
x = concatenate([action_input, flattened_observation])
x = Dense({{choice([16, 32, 64, 96, 128])}})(x)
x = Activation('relu')(x)
x = Dense({{choice([16, 32, 64, 96, 128])}})(x)
x = Activation('relu')(x)
x = Dense({{choice([16, 32, 64, 96, 128])}})(x)
x = Activation('relu')(x)
x = Dense(nb_actions)(x)
x = Activation('linear')(x)
critic = Model(inputs=[action_input, observation_input], outputs=x)
print(critic.summary())
memory = SequentialMemory(limit={{randint(100000)}}, window_length=1)
random_process = OrnsteinUhlenbeckProcess(size=nb_actions,
theta={{uniform(0,1)}}, mu={{normal(0,5)}}, sigma={{normal(3,3)}})
agent = DDPGAgent(nb_actions=nb_actions, actor=actor, critic=critic, critic_action_input=action_input,
memory=memory, nb_steps_warmup_critic=301, nb_steps_warmup_actor=301,
random_process=random_process, gamma=1, target_model_update={{loguniform(-7,-2)}},
batch_size={{choice([8,16,32,64,256,512,1024,2056])}})
agent.compile(Adam(lr={{loguniform(-7,-2)}}), metrics=['mae'])
# Train; ~120 steps/s, so train for ~8 hours:
agent.fit(env, nb_steps=3000000, visualize=False, verbose=1, nb_max_episode_steps=1000)
# After training is done, we save the final weights.
agent.save_weights('ddpg_{}_weights.h5f', overwrite=True)
# Finally, evaluate our algorithm for n episodes.
h = agent.test(env, nb_episodes=2000, visualize=False, nb_max_episode_steps=1000)
reward = numpy.mean(h.history['episode_reward'])
print "Reward: ", reward
return {'loss': -reward, 'status': STATUS_OK, 'model': agent}
def data():
return [], [], [], []
if __name__ == '__main__':
best_run, best_model = optim.minimize(model=model,
data=data,
algo=tpe.suggest,
max_evals=120, # 8h each, 4 per day, 30 days, so 120 trials
trials=Trials())
print("Best performing model chosen hyper-parameters:")
print(best_run)How could this be improved?
fix the output scaling to be a fraction of current wealth rather than a fixed amount of $250; this avoids forcing the NN to learn to change its actions based on current wealth just to keep a constant bet amount, and instead focus on learning deviations from the baseline Kelly small bet of ~12%
experiment with batchnorm in the critic as well
incorporate the exact value function into the training to see how much benefit the additional supervision provides and how much damage is caused by the RL setting, or pre-populate the experience replay buffer based on samples from the exact value function or the 12% heuristic; it might also be interesting to see how much pretraining on the simple Kelly coin-flip helps with training on the general Kelly coin-flip
experiment with additional regularization methods like L2 norm (which et al 2015 also used)
try variants on the environment:
scale rewards down to 0–1; deep RL approaches reportedly have trouble with rewards which are not on the unit-scale
instead of under-betting=$0 and overbetting=current wealth, make them illegal bets which terminate an episode
External Link
“The Gambler’s Problem and Beyond”, et al 2019
That is, the value of the actions/bets 0-w seems like it would be bitonic—increasing linearly to the maximum then linearly decreasing. So one ought to be able to do a binary search over actions or something even better. I assume this is related to Bellman’s proof that finite-horizon MDPs’ value functions are convex and piecewise linear.↩︎
Presumably a 3×5 or smaller NN would also work, but I experienced convergence issues with the SGD optimizer for all 3-layer NNs I experimented with, and as of 2017-03-29, a MXNet bug blocked use of the better optimizers.↩︎
I also tried its CEM implementation, but after trying a variety of settings, CEM never performed better than an average reward of 0.4 or ~$120, inferior to most DDPG runs.↩︎
This follows the original et al 2013 implementation. The NN is constructed with the screen observation state as the input and a final top layer outputting n reals corresponding to the q-value of the n actions, in that case the fixed number of buttons on the Atari controller. This allows enumeration of all possible actions’ values in a single forward pass of the NN, and picking the maximum… The alternative would be to input both the screen observation and one possible action, and get out a single q-value for that one action; then to act, the agent would loop over all possible actions in that state, and then finding the maximum actions, which would allow a varying number of possible actions in each state, but at the cost of doing n forward passes (one for each possible action). In the Atari setting, the DQN agent interacts exclusively through the controller which has only a few buttons and a directional pad; and the environments are complex enough that it would be hard to define in advance what are the valid actions for each possible screen, which is something that must be learned, so this fixed-action trick is both necessary and efficient. Thus, it is also used in most implementations or extensions of DQN. In the Kelly coinflip, on the other hand, the discretizing is problematic since the majority of actions will be invalid, using an invalid action is damaging since it leads to overbetting, and we can easily define the range of valid actions in each state (0-w), so the trick is much less compelling.↩︎