Estimation of catnip immunity rates by country with meta-analysis and surveys, and discussion of catnip alternatives.
Not all cats respond to the catnip stimulant; the rate of responders is generally estimated at ~70% of cats. A meta-analysis of catnip response experiments since the 1940s indicates the true value is ~62%. The low quality of studies and the reporting of their data makes examination of possible moderators like age, sex, and country difficult. Catnip responses have been recorded for a number of species both inside and outside the Felidae family; of them, there is evidence for a catnip response in the Felidae, and, more uncertainly, the Paradoxurinae, and Herpestinae.
To extend the analysis, I run large-scale online surveys measuring catnip response rates globally in domestic cats, finding high heterogeneity but considerable rates of catnip immunity worldwide.
As a piece of practical advice for cat-hallucinogen sommeliers, I treat catnip response & finding catnip substitutes as a decision problem, modeling it as a Markov decision process where one wishes to find a working psychoactive at minimum cost. et al 2017 measured multiple psychoactives simultaneously in a large sample of cats, permitting prediction of responses conditional on not responding to others. (The solution to the specific problem is to test in the sequence catnip → honeysuckle → silvervine → Valerian.)
For discussion of cat psychology in general, see my Cat Sense review.
Catnip (Nepeta cataria) is a plant which causes stimulated and excitable behavior in many domestic cats, which is fun to play with. It is the best known of at least a dozen plants with psychoactive effects on cats, and far more popular, cheaper, and easily purchased than alternatives like Tatarian honeysuckle, silvervine, or cat thyme. However, a large fraction of cats do not respond to catnip, but may respond to one of the alternatives. (For example, of my family’s two cats, neither responds to catnip but one responds to valerian, one to honeysuckle, and both to silvervine.)
This raises several questions:
-
what fraction of cats, exactly, are catnip-immune?
-
how often do the catnip alternatives work?
-
does immunity to one alternative predict immunity to others?
-
since some alternatives can be hard to find and expensive, what is the optimal order of alternatives a cat owner should try to find one that works?
Population Frequency of Catnip Response
Literature Review
Catnip is frequently discussed in the popular & secondary literature without citation, and after tracking down claims, the primary literature on catnip effects & response is relatively small1, with most research focused on the chemical synthesis of the active ingredients, botanical studies, or investigating the possible commercial applications as insecticide & insect repellent; the best literature review remains 1987. Key papers:
-
et al 1942, “The constituents of the volatile oil of catnip. II. The neutral components. Nepetalic anhydride”:
tested extracted nepetalactone and caryophyllene on 10 lions of unspecified but mixed genders/ages; the 7 adults all responded to the nepetalactone and not the caryophyllene (the 3 cubs responded to nothing).
-
1962, “Inheritance of the catnip response in domestic cats”
14 responders, 12 non-responders in a Siamese breeding colony so 46% immunity rate in this sample. (8 male responders, 6 female responders, 2 male non-responders, 10 female non-responders.) Todd also surveyed cats in local animal shelters/hospitals, finding 26 of 84 sampled were non-responders or a ~31% immunity. Todd considers the genetic pattern most consistent with a fairly common genetic variant (by Hardy-Weinberg: p2 + 2pq; p2 + 2pq = 0.69; q2 = 0.31, then p = 0.44; q = 0.56) which is autosomal dominant; this would imply that breeding cats for catnip response is highly feasible.
-
1963, “The catnip response”
-
In surveying the 26 breeding colony & 84 local cats, Todd found no large correlations with sex, breed type (Manx/Siamese/tabby/Agouti), white spotting, blue dilution, polydactyly, long hair, or castration. (32 male responders, 11 male non-responders, 26 female responders, 15 female non-responders.) Except the usual observation that young kittens rarely display a catnip response: of 39 under 12 weeks of age, 4 responded.
-
Cross-species results:
-
Viverrids (pg42/73), unspecified gender/age/species:
Table 3. Results of testing Viverrids with catnip. Figure in parentheses indicates number of individuals tested.
+= positive,?+= possibly positive,?-= probably negative,-= negative,I= indeterminate, animal would not or did not investigate leaves.Sub-families
Genera
N
+
?+
?-
-
I
Viverrinae
Genetta
3
0
0
0
2
1
Viverrinae
Viverra
1
0
0
1
0
0
Viverrinae
Civettictis
2
0
0
0
1
1
Paradoxurinae
Nandinia
5
0
0
3
2
0
Paradoxurinae
Paguma
2
0
0
1
0
1
Paradoxurinae
Arctictis
3
1
1
0
0
1
Herpestinae
Herpestes
1
0
0
0
1
0
Herpestinae
Atilax
3
0
1
1
1
0
Herpestinae
Ichneumia
1
0
0
0
0
1
Cryptoproctinae
Cryptoprocta
1
0
0
1
0
0
-
Hyenas (Hyenidae): 0⁄3 responders of 2 males/1 female (pg41/72), unspecified age, genus, or species, presumably either spotted or striped hyenas.
-
Felidae: (pg42/74). Todd’s table and results have been summarized as thus by Tucker & Tucker:
Within the subfamily Pantherinae of the Felidae, Todd (1963) found the typical catnip response in 16 lions (Panthera leo) (14 positive responders, 2 negative responders), 23 tigers (Panthera tigris) (8 incomplete responders, 13 negative responders, 2 inconclusive responders), 18 leopards (Panthera pardus) (14 positive responders, 4 negative responders), 8 jaguars (Panthera onca) (7 positive responders, 1 negative responder), 4 snow leopards (Panthera uncia) (4 positive responders), and 1 clouded leopard (Neofelis [Panthera] nebulosa). Within the subfamily Acynonychinae of the Felidae, he found that 3 cheetahs (Acinonyx jubatus) did not respond to catnip. Within the subfamily Felinae of the Felidae, he found the typical catnip response in the 2 bobcats (Felis [Lynx] rufus) (1 positive responder, 1 negative responder), 1 European lynx (Felis [Lynx] lynx), 5 pumas (Felis [Puma] concolor) (2 positive responders, 2 negative responders, 1 inconclusive responder), 1 Asiatic golden cat (Felis [Profelis] temmincki), 5 ocelots (Felis [Leopardus] pardalis) (4 positive responders, 1 negative responder), and 6 margay cats (Felis [Leopardus] wiedii) (4 positive responders, 2 negative responders); no catnip response was observed in 2 servals (Felis [Leptailurus] serval), 1 swamp cat or jungle cat (Felis chaus), 1 Pallas’ cat (Felis [Octocolobus] manul), 1 leopard cat (Felis [Prionailurus] bengalensis), 1 African golden cat (Felis [Profelis] aurata), 2 fishing cats (Felis [Prionailurus] viverrina), 4 jaguarundis (Felis [Herpailurus/Puma] yagouaroundi), and 1 pampas cat (Felis [Lynchailurus] pajeros).
The summary of Todd’s Felidae results is correct but omits that Todd also used a questionnaire to estimate 4 responders & 13 non-responders among the ocelots in addition to his personal testing of the 5 ocelots but Todd notes he “has reservations about the validity of the data gathered by this method” (possibly because the response frequency 4⁄17 is so different from his personal 4⁄5 response frequency) so that data is probably best excluded. Todd also mentions a report of a “ligeress” (female hybrid of a male lion & tigress) from de Bary of the Utah Hogle Zoological Garden who is a catnip non-responder. For the meta-analysis, I code the ‘questionable’ positive/negative responses as confirmed responses. Sex is usually unspecified, but individual-level data is provided on the lions, tigers, & leopards. I excluded the pampas cat and additional questionnaire data in line with Todd’s notes that the data were highly unreliable.
-
-
-
1963, “Terpenoids. Cis-trans- and trans-cis- nepetalactones”
They chemically separated the two isomers; the extracted isomer I was mostly inactive when presented to 8 cats with just 1 more interested in I than II (though they caution there might still have been contaminating II in the I extract), but “three were strongly attracted” and “two showed slight preference” for isomer II (_trans-cis-_nepetalactone), so arguably 5 out of 8 were responders. (Breed and sexes unspecified.)
-
1936, “Behavioral Ecology of Feral House Cats in the Galapagos Islands, Ecuador”: wild survey of cats; notes successful use of traps baited with tuna fish & catnip.
-
1966, “Catnip and oestrous behavior in the cat”
Reactions: 23 responders, 20 non-responders, so 47% immunity rate. (37 male, 28 female, mixed breeds: 6 male responders, 6 male non-responders, 9 castrated male responders, 5 castrated male non-responders, 5 female responders, 5 female non-responders, 3 spayed female responders, 4 spayed female non-responders.)
-
1968a, “Pseudo-Affective Reflexes of Cats produced by Extracts from the Plant Actinidia polygama” claims to have found no responses in an unspecified but probably >4 number of cats (as he used “young and old cats of both sexes”) when testing nepetalactone (catnip) and actinidine solutions, aside from two actinidine reactions
-
1968b, “Motor reflexes of cats to Actinidia polygama (Japan) and to catnip (USA)”
A 1966 conference talk published in the 1968 proceedings, 1968 is light on details. Tucker & Tucker summarize it as “Hayashi (1968), who tested a wide range of animals (dogs, rabbits, mice, rats, guinea pigs, fowls, and cats) with powders of Actinidia polygama and N. cataria, found that the catnip response is induced in cats alone.”, which tells one about as much as the original report does:
…actinidine (1) and catnip…have always been the source of much interest…When powder of these plants was presented to cats, they displayed a peculiar behavior…The reflex behavior is induced by the smell, not by taste and not via the circulation. The cat must be tamed by the experimenters and must be adult: male or female are quite the same…Once I tried with English cats in London, and with American cats in New York, each time taking advantage of visiting my friend’s laboratories, but English as well as American cats were rather cold…We tried experiments with dogs, rabbits, mice, rats, guinea pigs and also with fowls but they had no such reflexes to the plant powder…From these results, we presume that the reflex ability is restricted to cats and feline species in vertebrates, and its reflex centre would be situated in the subcortical, presumably limbic, structures…That the phenomenon is restricted to the cat family is said also in Japan.
-
Q[J.W. Johnson Jr]: This is a simple question that might be relevant to your point, Doctor. In Northern Virginia, where I live, there are stands or clumps of catnip. I’m not aware of house cats visiting the catnip stands while in the living state. Do you know whether this has been reported. -
A[T. Hayashi]: No, I don’t think so. We have natural growths of bushes of actidinia polygama in several parts of Japan, but nobody noticed that these bushes attracted cats from the villages….In the central part of Japan we have many actidinia distributed from north to south. But I have not heard that cats gather in the stands of the plant. Maybe the drying of the plants or burning of them is the most effective.
From this I gather that Hayashi must have tested at least 2 cats in the USA, 2 in the UK, and 2 in Japan (because he always uses the plural “cats”, and he compares the US/UK cats to Japanese cats). 1968a implies >=4 cats were used but not their national distribution. To be conservative in lieu of more precise data, one would have to code the Hayashi data as 2 cats per country. He does mention that the USA/UK cats were “rather cold”, which implies an intermediate but existent response much less than the Japanese cats. (It is also intriguing given et al 1988’s later possible implication that 16 of 16 cats in Japan reacted to catnip but not foreign breeds.) If we assume the n of each group of cats is 2, then the response rate must be 1/1/2 respectively, as otherwise Hayashi would either have described it as no response like the other species or as the same response as the Japanese cats. The other species are also pluralized, so at least 2 of each, and all responses must have all been 0 responders since “they had no such reflexes” and it is “restricted to cats and feline species”. Specific species (presumably the other animals are either domestic or lab species), sexes, breeds, and ages are not given.
-
-
et al 1969, “Feline Attractant, cis,trans-Nepetalactone: Metabolism in the Domestic Cat”
In a metabolic study, purified nepetalactone was force-fed to 6 cats in gel capsules; as expected due to the olfactory requirement (previously demonstrated by Todd with surgical manipulations of olfaction), none of the cats exhibited the catnip response and the result is irrelevant.
-
1972, “Effect of drugs on catnip (Nepeta cataria) induced pleasure behavior in cats”
Tested 17 cats initially; 14 responders. (Mixed breed, both genders; breakdowns of response not given.) Hatch’s main effort was towards using drug administrations to block the catnip effects and undermine the sexual hormone hypothesis.
-
Todd as quoted in R.F. 1973, The Carnivores (pg244):
Differential aspects of the same scent on different species are illustrated in some unpublished work by Dr N.B. Todd, which he has kindly allowed me to quote. He tested the responses of various species to catnip and found that a number of viverrids, although clearly able to smell the catnip, showed little interest: for them it carried no message and had no particular significance. I have found the same to be true of Civettictis and Crossarchus [African dwarf mongoose]. In the Felidae, the cat-type sexual response was widespread but not universal. Amongst the large cats, lion, leopard, jaguar and snow leopard responded sexually but adult tigers did not. The behavior of immature tigers was interesting: they were not sexually excited but instead showed violent alarm and retreated promptly. In view of the propensity of the larger species of felids to kill each other’s young and of the fact that until quite recently the ranges of tiger and lion overlapped very considerably, both the absence of sexual response in the adult tiger and the fear generated in the young may be adaptive: the former may reflect a sexual isolating mechanism; the latter may be protective. Apart from illustrating differential responses to the same odour, these observations also demonstrate the psychological effects of odours. A piece of material impregnated with catnip is neither a mate nor an enemy but it can evoke sexual responses or flight: to do so it must act on the central nervous system so as to change the animal’s mood - in short, it “makes him sexy” or it “makes him afraid”.
Todd’s results here refer to his PhD thesis, but I have not found any Ewer publication on catnip thus far.
-
et al 1974, “Behavioral activity of catnip and its constituents: nepetalic acid and nepetalactone”/ et al 1978, “Behavioral and toxicological studies of cyclopentanoid monoterpenes from Nepeta cataria”
Considers only injections of catnip oil into mice/rats.
-
et al 1976, “Species-characteristic Responses to Catnip by Undomesticated Felids”; Tucker & Tucker summary (apparently based on counting the descriptions in Table 3 or Table 4):
et al 1976 found that lions (5 positive responders, 6 partial responders, 1 negative responder) and jaguars (3 positive responders) are extremely sensitive to catnip, while tigers (5 negative responders), pumas (4 negative responders), leopards (4 partial responders, 4 negative responders), and bobcats (2 negative responders) gave little or no response. They also found that both males and females of the same species test alike, while reproductive-age adults are more sensitive than either aged or immature animals.
-
1977, “Olfaction and feline behavior”: short popular summary of some aspects of cat olfactory capabilities; briefly mentions catnip.
-
1985, “Feral Cats on Jarvis Island: Their Effects and Eradication”:
Account of a Pacific Island; mentions use of catnip in traps, without success, and notes that van Aarde told Rauzon of “previous low success rates” using catnip as well; presumably van Aarde was referring to efforts on the South African Marion Island (of the Prince Edward Islands), since while the two cited van Aarde papers do not mention catnip, a 2002 followup on success cites one of the authors’ master theses as reporting failure in use of catnip oil (success ultimately coming from Feline panleukopenia disease followed by intensive hunting/trapping/poisoning):
-
van 1980, “The diet and feeding behavior of feral cats (Felis catus) at Marion Island”
-
van 1980, “Gene frequencies in feral cats on Marion Island, South Africa”: considerable skew in coat colors, indicating founder effect; interestingly, like the Kerguelen Islands ferals, the Marion Island cats are also heavily skewed towards black fur.
-
-
et al 1988, “Both (4a_S_, 7_S_, 7a_R_) -(+)-Nepetalactone and Its Antipode Are Powerful Attractants for Cats”
Another investigation of which isomers/enantiomers of nepetalactone are active, the isolated versions were tested in 9 cats with vials of the liquid; 7 responded (while the two 6-month olds didn’t and et al 1988 attributes the non-response to their being ‘immature’, 6 months sounds old enough for reactions to have developed). The cat breeds are specified as 4 Japanese, 3 Abyssinian, and 2 American short-hairs, but not sexes (although Sakurai used a mix, given their comments that “the females showed more emotional behavior than the males…the females were quite reactive, while the males were not…both of them [isomers] were extremely attractive to mature cats, especially to females”). Possibly contradicting 1963’s results where only 1 isomer worked, Sakurai finds both isomers work equally well.
Confusingly, Sakurai also mentions a second experiment in impregnating filter paper with the isomers, noting that “sixteen Japanese cats reacted to the 0.01mg dose”; it’s unclear where these cats came from when only 9 cats (4 Japanese) were mentioned for the first experiment, and whether they were selected out of a larger group of cats or if it’s implied that it was 16 out of 16 responders - inasmuch as with catnip response rates ~70%, it would be highly improbable for all of a group of 16 cats to be catnip responders (0.716=0.3%). One possible explanation is that Japanese cats, being a historically isolated population (eg. the Japanese Bobtail) after their introduction ~500AD from Korea, may have much higher population frequencies or even fixed the catnip mutation due to genetic drift or a founder effect2; on the other hand, if Japanese cats were almost all catnip responders, you would think someone would have noticed by now. My GS survey finds a ~28% immunity rate, which is not unusual at all, suggesting that Hayashi/Sakurai is some sort of sampling error or reporting effect.
-
1992, “Environmental enrichment in a large animal facility”:
TABLE 1. Number of animals, species-wide, that showed interest in various toys. Key: 0 = none, 1 = 25%, 2 = 50%, 3 = the majority of the animals. We define interest as the amount of toy destruction and/or movement that we noted in daily observations.
-
…balls: catnip: 3
-
balls: punch: 3
-
Cat-a-Comb: NA
-
Purrsuit: 3
…8-12 cats…The cats’ favorite toys - like the 12 in. giant sheepskin mice (Petraport, Anaheim, CA) - contained catnip. We hung fresh catnip in stockinette bags which the cats quickly pulled down and ultimately batted into the water bowls. We gave them catnip-treated punchball toys (Petraport, Anaheim, CA- Fig. 7)-2 in. puffs mounted by a spring to a 6 in. x 6 in. base. The cats always played with these toys, and they lasted longer than the catnip bags. The cats also had “Mr. Spats’ Cat-a-combs” groomer (Tarel Seven Designs, Secaucus, NJ) mounted on the walls. They usually knocked these off [of] the wall and used them as play-things (they managed to open the compartment and dig out the catnip) rather than as grooming tools. Most of the cats spent time playing “Purrsuit” (Tarel Seven Designs, Secaucus, NJ)-every morning, we placed toys inside a maze and the cats chased them and tried, with a great deal of success, to get the smaller ones out. The cats had a preference for balls or bells with catnip in them, and for golf balls. They ignored the Squish balls (Ethical Inc., Newark, NJ).
So based on the reported data, we can guess that at least 5-7 cats responded to catnip of the 8-12 sample, for a best guess of 6 responders out of 10 cats. (Mixed breeds, unspecified sex.)
-
-
et al 1992, “Toxic Bait and Baiting Strategies for Feral Cats”/ et al 1992, “Experimental Eradication of Feral Cats (Felis Catus) from Matakohe (Limestone) Island, Whangarei Harbour”: New Zealand, a mix of wild survey and experiment, employing a variety of baits & scents including catnip. Catnip performed well among the NZ feral cats: for example, 6 cats observed at dusk spent a mean ~200s investigating a catnip odor as opposed to <50s or ~0s for 3 urine scents (Figure 1), and counts of visits to catnip odor stations were far higher than for urine, fish oil, or water controls (Table 1: 25 vs 13/12/11). Catnip/catmint only performed poorly when used as a food flavoring in a commercial cat food (Figure 3), but then performing well alone & combined with L-alanine in bait (Figure 5/6). They then deployed their catnip & other baits to poison ~5 cats on Matakohe Island; the catnip bait did not lead to noticeably more bait consumption, but from the description, catnip response might not have been noticeable or just sampling error.
-
et al 1994, “Development and Testing of Attractants for Feral Cats, Felis catus L.”
Wild survey and experiment in New Zealand. Catnip & silvervine were tested as cat lures for trapping; simultaneous testing over multiple environments showed that catnip, silvervine, and urine all garnered substantial attention from cats. Clapperton notes that 4⁄4 domestics and 8⁄20 feral cats responded (pg7). (Sex not specified, but breeds were clearly mixed as feral cats are never single breeds.)
-
1997, “Chemical attractants for Central American felids”: experimental testing of jaguars, jaguarundi, little spotted cats, margays, ocelots, & pumas of catnip and other lures; Harrison reports the data in terms of time spent investigating and “behavior scores” (the number of observed behaviors such as sniffing/vocalizing/rubbing/rolling), and not in terms of individual responders. The reported data suggests some level of response in jaguars/jaguarundi/ocelots.
-
et al 1997, “Field evaluation of olfactory lures for feral cats (Felis catus L.) in central Australia”: wild survey in Australia; 15 kinds of lures were tested, pitting a catnip lure (#12) against various seafood, blood-bone mix, male/female cat urine/anal gland secretions; the 3 best olfactory lures were sun-dried prawns (#8) & male (#13)/female (#14) urine-secretions, but not catnip - catnip received 2 cat visits while the best 3 received 17/14/7 respectively. Edwards notes their surprise at the inefficacy of the catnip compared to the urine-secretions, as et al 1994 had found catnip much superior in their NZ experiment and ask, “do cats from different areas respond differently to different olfactory stimuli?”
-
et al 2000, “Efficacy of lures and hair snares to detect lynx”
Used catnip and other commercial products in scent stations to look for activity of wild lynx. 1963 had already found responses in lynx/puma/bobcats, so unsurprisingly McDaniel does too, but with wild lynx, it is impossible to know how many total lynx were exposed and how many reacted.
-
2001, “Trapping and demographics of feral cats (Felis catus) in central New South Wales”: Australian live trapping study using varied baits; a bait combination of catnip/tuna oil/“synthetic fermented eggs” (SFE); while a small sample, the success in terms of cats trapped per 100 trap-nights varied from 0.5 (fish) to 3.8 (“PUSSON” baits + aluminum toys on string), with the catnip mix at 1.1, suggesting little or no advantage over other baits like rabbit.
-
et al 2002, “Control of feral cats for nature conservation. III. Trapping”: Australian trapping study, varying bait and timing. Fresh catnip bait ranked roughly median, below rabbit/mice/2 commercial mixes; catnip worked well in the first trapping and then poorly afterwards, the authors speculating that the decline is “perhaps due to removing the pool of susceptible individuals.” (Total catching: 8 cats out of 118; in a head to head test of 2 traps, one catnip and a commercial mix, the catnip trap caught 8 vs 7.)
-
2004, “The influence of olfactory enrichment on the behavior of captive black-footed cats, Felis nigripes”:
6 black-footed cats (Felis nigripes), catnip did interest them and cause increases in activity, but paper doesn’t break down by cat. Not useful unless want to contact authors for individual-level data.
-
et al 2005, “Use of scented hair snares to detect ocelots”: tested 32 ocelots available in 9 facilities, as well as a wild survey; 27 of the 32 responded to their bait, which was a combination of a mix “Weaver’s Cat Call” and dried catnip; Weaver reports that the combination was earlier established in bobcats & lynx to be much more effective than catnip alone, so 84% represents an overestimate of catnip’s effect on ocelots.
-
2007, “Sensory enrichment for cats (Felis silvestris catus) housed in an animal rescue shelter”; apparently republished as 2010, “The influence of olfactory stimulation on the behavior of cats housed in a rescue shelter”
Shelter animals were given catnip-infused clothes to play with; Ellis notes that the catnip toys were played with more than other scents on average in the catnip group, but made no effort to ascertain how many were catnip responders.
-
et al 1995, “Behavioral effects of acute and long-term administration of catnip (Nepeta cataria) in mice”; et al 2010, “Antidepressant-like effects of an apolar extract and chow enriched with Nepeta cataria (catnip) in mice”
There is apparently a vein of studies trying catnip in humans for antidepressant effects (rather than the more traditional painkiller and psychedelic effects), leading to this experiment in chronic feeding catnip to mice (ironic as that might sound), finding one antidepressant-like effect. These can’t be considered a catnip response, though.
-
2006, “Using Scent-Marking Stations to Collect Hair Samples to Monitor Eurasian Lynx Populations” / et al 2013, “Hair snaring and molecular genetic identification for reconstructing the spatial structure of Eurasian lynx populations”: wild survey using catnip oil and beaver oil; 29 unique individuals genotyped
-
et al 2007, “Hair Snares for Noninvasive Sampling of Felids in North America: Do Gray Foxes Affect Success?”: wild sampling in Mexico; catnip oil did not attract any of the target margay wild cats, but did attract many gray foxes & 14 domestic cats.
-
et al 2007, “Comparing Scat Detection Dogs, Cameras, and Hair Snares for Surveying Carnivores”: wild survey, used dried catnip; no detection of bobcats
-
Castro- et al 2008, “Hair-Trap Efficacy for Detecting Mammalian Carnivores in the Tropics”: wild survey in Mexico, comparing perfume & catnip oil, finding catnip oil inferior
-
The 8 oncilla cats’ activity were measured over several days after each dose was introduced into their enclosures. While the doses were small (1g), the cinnamon produced statistically-significant overall average difference while catnip did not, suggesting none of the oncilla cats responded to the catnip. Nevertheless, like 2004, cannot be meta-analyzed.
-
et al 2011, “Bobcats Do Not Exhibit Rub Response Despite Presence at Hair Collection Stations”: wild survey using catnip oil; no near-zero rubbing
-
2012, “A Comparison of Noninvasive Survey Methods for Monitoring Mesocarnivore Populations in Kentucky”: wild survey; did not break down detection rates by lure type
-
2013, “Sniffing out the stakes: hair-snares for wild cats in arid environments”: Australian wild survey; catnip & valerian proved ineffective in attracting cats to the stakes, and they suggest that Australian wildcats (apparently descended from domesticated cats) may simply be catnip immune, noting their results parallel Molsher 2001 & et al 2002. (This may be connected to Australia’s import regulations which deter bringing new cats into the country: a number of hybrid breeds are banned as well as origin countries; and legal cats must be: permitted, microchipped, rabies-vaccinated at least 180 days in advance & tested to confirm immunity, not be too pregnant, treated for internal parasites, treated for external parasites, clinically examined by a Australian-government-approved veterinarian, and quarantined for at least 10 days.)
-
et al 2013, “Assessing the efficacy of hair snares as a method for noninvasive sampling of Neotropical felids” (Table 1): wild survey and experiment of cinnamon/vanilla/catnip scent lures on 5 jaguars (Panthera onca)/10 ocelots (Leopardus pardalis)/6 oncilla cats (Leopardus tigrinus)/7 margay cats (Leopardus wiedii)/6 pumas (Puma concolor)/5 jaguarundis (Puma yagouaroundi). The wild survey yielded no results, while the captive experiment indicated that the puma did not interact with any lures and at least some of the ocelot/margay/oncilla did, with the strongest effect being vanilla.
As et al 2013 measures behavior in length of time interacting with the scent lures and reports only species-level differences, it is impossible to say what fraction of the cats were responders, other than the total lack of response of the 6 pumas to any scents showing that 0⁄6 of them responded.
-
et al 2016, “Identification of the Cat Attractants Isodihydronepetalactone and Isoiridomyrmecin from Acalypha indica”, reporting on Acalypha indica, mentions in passing (without numbers, and apparently not reported elsewhere) that
Christmas Island is a small island off the north-west coast of Australia that is well known for its unique flora and fauna…One particular project has been attempting to reduce the large number of feral cats on the island [4] and during this project, the research team became aware of a plant that several local residents suggested had a peculiar effect on cats when the roots of the plant were exposed…There are plants such as catnip (Nepeta cataria) which have similar effects on cats due to the presence of nepetalactone. [9] However, investigation of catnip by the Christmas Island research team found that this plant had no effect on the Christmas Island cats.
Founder effect?
-
Poddar-2014, “Chapter 15: Pheromones of Tiger and Other Big Cats” note an unreported attempt at measuring catnip response rates in wild African lions:
Certain persons brought catnip from England to George Adamson’s lion camp in Kora, Kenya, and tried to study the effect of this plant on the African lion but no conclusive results were obtained (1988, personal communication).
-
et al 2015, “Sneaky felids, smelly scents: a small scale survey for attracting cat”: wild survey in Hungary, comparing catnip with salmon oil/valerian/commercial-scent; 1 stone marten & 3 cats rubbed the catnip, 4 valerian, none otherwise.
-
et al 2016, “More Hair than Wit: A Review on Carnivore Related Hair Collecting Methods”: literature review on wild surveying; no particular conclusions drawn on catnip.
-
2017, “An assessment of the efficacy of rub stations for detection and abundance surveys of Canada lynx (Lynx canadensis)”: a wild survey; the lynx did use both the beaver castor & catnip oil rub stations but, like et al 2000, the method does not permit any quantification of response rates in the Canada lynx although the authors infer it was <100% since the catnip oil rub stations did not work as well as the standard camera traps.
-
et al 2017, “Social interaction, food, scent or toys? A formal assessment of domestic pet and shelter cat (Felis silvestris catus) preferences”: experimental test of 25 pet & 25 animal shelter cats’ preferences by offering the stimuli simultaneously and measuring proportion of time on each to extract a “choice”; for example, in the olfactory category, of the 38 cats, 6 ‘chose’ the gerbil, 6 the cloth rubbed on another cat’s scent glands (“conspecific”), and 22 the catnip. However, while 22⁄38 = 0.58 may look like a plausible estimate of catnip response in this sample, that would be making some strong assumptions, as Shreve et al do not mention trying to classify catnip response, and the choice is ambiguous: 22 of 38 cats finding catnip the most interesting smell does not mean 22 had a catnip response - as any of the 22 might not have had a response but simply found the catnip a more pleasing or novel smell, and vice versa for the other.
-
et al 2017, “Responsiveness of cats (Felidae) to silver vine (Actinidia polygama), Tatarian honeysuckle (Lonicera tatarica), valerian (Valeriana officinalis) and catnip (Nepeta cataria)”: one of the most thorough studies, using both a large number of cats (n = 100) and the 4 major cat stimulants, et al 2017 is an impressive experiment. It’s worth highlighting that the 4 stimulants were offered to the same set of cats, allowing measurement of intercorrelations, cats were exposed at least twice with attention given to a low-stress administration (reducing measurement error, as emphasized by 2011), gas chromatography was used for a chemical analysis, the sample size is one of the largest ever (exceeded only by /2013 and my surveys), the partnership with Big Cat Rescue extends the results to several other interesting species (bobcats & tigers), and the full dataset is included with the paper.
I extract 2 CSVs from the raw data, for cats & bobcats/tigers. Code responses of “5” or “10” (mild vs intense) are considered responders; Bol states that “Because most (80–90%) of the cats studied were (blends of) domestic short-haired breeds, we did not study associations between breed and responsiveness to the materials tested”, so the cats are all coded as “American short-hair” breeds. Testing was done in the USA. Tigers/bobcats were likewise coded as responders if they had “5”/“10” codes for catnip. Summary:
-
22⁄34 male cats responded
-
38⁄55 female cats responded
-
2 male tigers, both non-responders
-
7 female tigers, 1 responder
-
1 female bobcat, 1 responder
-
-
Espín- et al 2017, “Active and passive responses to catnip (Nepeta cataria) are affected by age, sex and early gonadectomy in male and female cats”
Espín- et al 2017 argues (following et al 1976) that catnip response has been wrongly conceived as an active or non-responder (baseline) binary, and “non-responders” are in fact responding in a different way by moving much less & adopting the “sphinx” posture (based on computerized scoring of videotape in a cylindrical chamber after exposure to catnip). Their results also suggest that older, male, and early-neutered cats are more passive responders. This would suggest catnip is a drug capable of both stimulant and depressive effects, like nicotine or marijuana or alcohol (although catnip would not seem to depend on dose, only individual differences).
-
et al 2018, “Effect of a Synthetic Feline Pheromone for Managing Unwanted Scratching”: commercial study which included 0.1% catnip in anti-scratching solution product with reportedly good results, but effect is confounded and can’t infer individual cat response rates
-
et al 2018, “Effect of a Nepeta cataria oil diffusor on cat behaviour”: paper in Italian; English abstract indicates it was a n = 20 (10:10) between-group study of a catnip essential oil aromatic diffuser; results:
Based on owner answers, 90% [9⁄10] of cats of the therapy group and 40% [4⁄10] of cats of the control group showed an improvement (p ≤ 0.05). Play behavior increased in the therapy group and decrease in the control one (p = 0.06). The percentage of cats showing hissing or biting attempts toward other cats and scratching doors decreased statistically-significantly in the therapy group (p ≤ 0.05) and increased in the control one. Similar trend was seen for cats changing room to go away from other animals and we found a statistically-significant difference between the two groups before (p ≤ 0.05) and post-treatment (p = 0.081).
Given the considerable improvement in the control group, the 9⁄10 can’t be interpreted as a response rate. If we subtract the control group’s 4⁄10 as a baseline for regression to the mean or owner-placebo-effect, the 5⁄10 is a plausible result for catnip response, but is indirect enough that I think it’s probably better to leave it out of the meta-analysis.
-
et al 2011, “Repellent activity of catmint, Nepeta cataria, and iridoid nepetalactone isomers against Afro-tropical mosquitoes, ixodid ticks and red poultry mites”; although this is not described anywhere in the text of et al 2011, according to et al 2019:
et al 2011 synthesized the unnatural (4aR,7R,7aS)-nepetalactone and enantiomer of (4aS,7S,7aR)-nepetalactone. These two molecules have been bioassayed against two American short-hair, three Abyssinian, and four Japanese cats. Almost all cats reacted strongly especially the female ones towards both the enantiomers. Female cats have been found to be extremely attractive even at the dose of 0.01 mg.
et al 2019 seems to have either omitted a citation or confused et al 2011 with et al 1988.
-
Tested catnip/valerian/cinnamon on 3 lynxes. Catnip resulted in substantially more interaction, but Jean-2019 analyzes & visualizes only by totals, not breaking it down by lynx, so no estimate of whether it’s 1/2/3 responders is possible.
TODO:
-
2006, “A comparison of survey methods for detecting bobcats”
-
2011, “Heritability and Characteristics of Catnip Response in Two Domestic Cat Populations”
Potentially relevant but currently unavailable:
-
2013, “Genome-Wide Association Study for Catnip Response in Domestic Cats”: unpublished research, but abstract of results; TODO: email Leslie Lyons and ask if published anywhere or if the dataset can be made public; the catnip response rate would be informative, there may be other genetic analyses, and would boost any future GWAS:
Results: No Significant Genetic Region Identified for Catnip Response in Cats. About 50% of cats respond to catnip. Funded by the Cat Health Network, researchers from the University of California–Davis tested 192 shelter cats for catnip response in controlled settings. DNA was collected from cats responding to catnip and compared to DNA of nonresponding cats. Genetic analysis of these samples did not reveal a causative gene associated with catnip response. Identification of genes responsible for catnip response may provide clues to the mechanisms involved in olfactory responses to drugs and chemicals in cats.
Overall, study quality is low and at high risk of bias. Key variables like sex/age/breed is almost always never reported and sometimes even n or species is not reported; placebo controls are not used; the experimenters are never blind to the substance being used; important studies are not available in English; the catnip used is not standardized; and the animals are not necessarily familiarized & comfortable with the experimenter despite the need for them to be relaxed and willing to play in order to gauge the presence or absence of a response. Probably any estimate is something of a lower bound as most of these biases would tend to mask a catnip response (like using old catnip or an animal feeling stressed), and it will be difficult to prove or disprove any sex or breed effects.
Data
catnip <- read.csv(stdin(), header=TRUE)
Family,Genus,Species,Name,Study, Year, Responders, N, Country, Sex, Breed
Felidae,Panthera,leo,African lion,McElvain et al 1942,1942,7,7,USA,mixed,NA
Viverrinae,Civettictis,NA,NA,Todd 1962,1962,0,3,USA,mixed,NA
Viverrinae,Viverra,NA,NA,Todd 1962,1962,0,1,USA,mixed,NA
Viverrinae,Civettictis,NA,NA,Todd 1962,1962,0,2,USA,mixed,NA
Paradoxurinae,Nandinia,NA,NA,Todd 1962,1962,0,5,USA,mixed,NA
Paradoxurinae,Paguma,NA,NA,Todd 1962,1962,0,2,USA,mixed,NA
Paradoxurinae,Arctictis,NA,NA,Todd 1962,1962,2,3,USA,mixed,NA
Herpestinae,Herpestes,NA,NA,Todd 1962,1962,0,1,USA,mixed,NA
Herpestinae,Atilax,NA,NA,Todd 1962,1962,1,3,USA,mixed,NA
Herpestinae,Ichneumia,NA,NA,Todd 1962,1962,0,1,USA,mixed,NA
Cryptoproctinae,Cryptoprocta,NA,NA,Todd 1962,1962,0,1,USA,mixed,NA
Hyaenidae,NA,NA,hyena,Todd 1962,1962,0,1,USA,F,NA
Hyaenidae,NA,NA,hyena,Todd 1962,1962,0,2,USA,M,NA
Felidae,Panthera,leo,African lion,Todd 1962,1962,6,6,USA,M,NA
Felidae,Panthera,leo,African lion,Todd 1962,1962,8,10,USA,F,NA
Felidae,Panthera,tigris,tiger,Todd 1962,1962,1,9,USA,M,NA
Felidae,Panthera,tigris,tiger,Todd 1962,1962,7,13,USA,F,NA
Felidae,Panthera,leo/tigris,ligeress,Todd 1962,1962,0,1,USA,F,NA
Felidae,Panthera,pardus,leopard,Todd 1962,1962,6,8,USA,M,NA
Felidae,Panthera,pardus,leopard,Todd 1962,1962,8,10,USA,F,NA
Felidae,Panthera,onca,jaguar,Todd 1962,1962,4,5,USA,M,NA
Felidae,Panthera,onca,jaguar,Todd 1962,1962,3,3,USA,F,NA
Felidae,Panthera,uncia,snow leopard,Todd 1962,1962,2,2,USA,M,NA
Felidae,Panthera,uncia,snow leopard,Todd 1962,1962,2,2,USA,F,NA
Felidae,Neofelis,nebulosa,clouded leopard,Todd 1962,1962,1,2,USA,NA,NA
Felidae,Acinonyx,jubatus,cheetah,Todd 1962,1962,0,3,USA,NA,NA
Felidae,Felis,rufus,bobcat,Todd 1962,1962,1,2,USA,NA,NA
Felidae,Felis,lynx,European lynx,Todd 1962,1962,1,1,USA,NA,NA
Felidae,Felis,concolor,puma,Todd 1962,1962,2,3,USA,M,NA
Felidae,Felis,concolor,puma,Todd 1962,1962,1,2,USA,F,NA
Felidae,Felis,temmincki,African golden cat,Todd 1962,1962,1,1,USA,NA,NA
Felidae,Felis,aurata,Asian golden cat,Todd 1962,1962,0,1,USA,NA,NA
Felidae,Felis,pardalis,ocelot,Todd 1962,1962,4,5,USA,NA,NA
Felidae,Felis,wiedii,margay,Todd 1962,1962,4,6,USA,NA,NA
Felidae,Felis,serval,serval,Todd 1962,1962,0,2,USA,NA,NA
Felidae,Felis,chaus,swamp cat,Todd 1962,1962,0,1,USA,NA,NA
Felidae,Felis,manul,Pallas cat,Todd 1962,1962,0,1,USA,NA,NA
Felidae,Felis,bengalensis,leopard cat,Todd 1962,1962,0,1,USA,NA,NA
Felidae,Felis,viverrina,fishing cat,Todd 1962,1962,0,2,USA,NA,NA
Felidae,Felis,yagouaroundi,jaguarundi,Todd 1962,1962,0,4,USA,NA,NA
Felidae,Felis,pajeros,pampas cat,Todd 1962,1962,0,1,USA,NA,NA
Felidae,Felis,catus,cat,Todd 1962,1962,8,10,USA,M,Siamese
Felidae,Felis,catus,cat,Todd 1962,1962,6,16,USA,F,Siamese
Felidae,Felis,catus,cat,Todd 1963,1963,32,43,USA,M,mixed
Felidae,Felis,catus,cat,Todd 1963,1963,26,41,USA,F,mixed
Felidae,Felis,catus,cat,Bates & Siegel 1963,1963,5,8,USA,NA,NA
Felidae,Felis,catus,cat,Palen & Goddard 1966,1966,15,26,USA,M,mixed
Felidae,Felis,catus,cat,Palen & Goddard 1966,1966,8,17,USA,F,mixed
Felidae,Felis,catus,cat,Hayashi 1968,1966,1,2,USA,NA,NA
Felidae,Felis,catus,cat,Hayashi 1968,1966,1,2,UK,NA,NA
Felidae,Felis,catus,cat,Hayashi 1968,1966,2,2,Japan,NA,NA
Canidae,Canis,lupus,dog,Hayashi 1968,1966,0,2,Japan,NA,NA
Leporidae,Oryctolagus,cuniculus,rabbit,Hayashi 1968,1966,0,2,Japan,NA,NA
Muridae,Mus,musculus,mouse,Hayashi 1968,1966,0,2,Japan,NA,NA
Muridae,Rattus,norvegicus,rat,Hayashi 1968,1966,0,2,Japan,NA,NA
Caviidae,Cavia,porcellus,guinea pig,Hayashi 1968,1966,0,2,Japan,NA,NA
Phasianidae,NA,NA,fowl,Hayashi 1968,1966,0,2,Japan,NA,NA
Felidae,Felis,catus,cat,Hatch 1972,1972,14,17,USA,mixed,mixed
Felidae,Panthera,leo,African lion,Hill et al 1976,1976,3,4,USA,M,NA
Felidae,Panthera,leo,African lion,Hill et al 1976,1976,5,5,USA,F,NA
Felidae,Panthera,onca,jaguar,Hill et al 1976,1976,1,1,USA,M,NA
Felidae,Panthera,onca,jaguar,Hill et al 1976,1976,2,2,USA,F,NA
Felidae,Panthera,pardus,leopard,Hill et al 1976,1976,2,4,USA,M,NA
Felidae,Panthera,pardus,leopard,Hill et al 1976,1976,2,4,USA,F,NA
Felidae,Panthera,tigrus,tiger,Hill et al 1976,1976,0,1,USA,M,NA
Felidae,Panthera,tigrus,tiger,Hill et al 1976,1976,0,4,USA,F,NA
Felidae,Felis,rufus,bobcat,Hill et al 1976,1976,0,1,USA,M,NA
Felidae,Felis,rufus,bobcat,Hill et al 1976,1976,0,1,USA,F,NA
Felidae,Puma,concolor,cougar,Hill et al 1976,1976,0,2,USA,M,NA
Felidae,Puma,concolor,cougar,Hill et al 1976,1976,0,2,USA,F,NA
Felidae,Felis,catus,cat,Sakurai et al 1988,1988,4,4,Japan,mixed,Japanese
Felidae,Felis,catus,cat,Sakurai et al 1988,1988,3,3,Japan,mixed,Abyssinian
Felidae,Felis,catus,cat,Sakurai et al 1988,1988,2,2,Japan,mixed,American short-hair
Felidae,Felis,catus,cat,Sakurai et al 1988,1988,16,16,Japan,NA,Japanese
Felidae,Felis,catus,cat,DeLuca & Kranda 1992,1992,6,10,USA,NA,mixed
Felidae,Felis,catus,cat,Clapperton et al 1994,1994,12,24,USA,NA,mixed
Felidae,Felis,concolor,puma,Portella et al 2013,2013,0,6,USA,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,695,842,Canada,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,615,783,USA,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,463,625,UK,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,228,320,Japan,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,216,380,Germany,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,174,313,Brazil,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,108,200,Spain,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,403,759,Australia,NA,NA
Felidae,Felis,catus,cat,Gwern 2017,2017,94,180,Mexico,NA,NA
Felidae,Felis,catus,cat,Bol et al 2017,2017,22,34,USA,M,American short-hair
Felidae,Felis,catus,cat,Bol et al 2017,2017,38,55,USA,F,American short-hair
Felidae,Felis,catus,cat,Bol et al 2017,2017,7,10,USA,NA,American short-hair
Felidae,Panthera,tigrus,tiger,Bol et al 2017,2017,1,7,USA,F,NA
Felidae,Panthera,tigrus,tiger,Bol et al 2017,2017,0,2,USA,M,NA
Felidae,Felis,rufus,bobcat,Bol et al 2017,2017,1,1,USA,F,NA
catnip$Sex <- ordered(catnip$Sex, levels=c("F", "mixed", "M"))
catnip$Country <- relevel(catnip$Country, "USA")Meta-Analysis
Cats Catnip Response Rate
A random-effects meta-analysis on the proportion of catnip response in domestic cats using metafor:
cat <- subset(catnip, Name=="cat")
sum(cat$Responders) / sum(cat$N)
# [1] 0.6795952782
library(metafor)
r <- rma(xi=Responders, ni=N, measure="PR", slab=Study, data=cat); summary(r)
# Random-Effects Model (k = 29; tau^2 estimator: REML)
#
# logLik deviance AIC BIC AICc
# 12.0648 -24.1296 -20.1296 -17.4652 -19.6496
#
# tau^2 (estimated amount of total heterogeneity): 0.0155 (SE = 0.0059)
# tau (square root of estimated tau^2 value): 0.1244
# I^2 (total heterogeneity / total variability): 92.25%
# H^2 (total variability / sampling variability): 12.90
#
# Test for Heterogeneity:
# Q(df = 28) = 382.1487, p-val < .0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# 0.6714 0.0288 23.3059 <.0001 0.6150 0.7279
png(file="~/wiki/doc/cat/psychology/drug/catnip/gwern-catnip-forest.png", width = 590, height = 610)
forest(r, xlim=c(0,1))
invisible(dev.off())
## some issues in the funnel plot of too-extreme values:
funnel(r); trimfill(r)
# ...Estimated number of missing studies on the right side: 0 (SE = 3.3070)
## Examine all moderators:
rall <- rma(xi=Responders, ni=N, measure="PR", slab=Study,
mods= ~ Year + Country + Sex + Breed, data=cat)
summary(rall)
# Mixed-Effects Model (k = 12; tau^2 estimator: REML)
#
# logLik deviance AIC BIC AICc
# 1.8566 -3.7133 16.2867 7.2728 236.2867
#
# tau^2 (estimated amount of residual heterogeneity): 0.0058 (SE = 0.0114)
# tau (square root of estimated tau^2 value): 0.0763
# I^2 (residual heterogeneity / unaccounted variability): 42.11%
# H^2 (unaccounted variability / sampling variability): 1.73
# R^2 (amount of heterogeneity accounted for): 16.14%
#
# Test for Residual Heterogeneity:
# QE(df = 3) = 5.3993, p-val = 0.1448
#
# Test of Moderators (coefficient(s) 2:9):
# QM(df = 8) = 10.3723, p-val = 0.2399
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# intrcpt 112.4174 80.1102 1.4033 0.1605 -44.5957 269.4304
# Year -0.0553 0.0397 -1.3935 0.1635 -0.1330 0.0225
# CountryJapan -2.0805 1.4876 -1.3986 0.1619 -4.9961 0.8351
# Sex.L 0.0799 0.0592 1.3497 0.1771 -0.0361 0.1960
# Sex.Q -0.5159 0.2766 -1.8651 0.0622 -1.0581 0.0263
# BreedAmerican short-hair -0.0417 0.2920 -0.1427 0.8865 -0.6141 0.5307
# BreedJapanese 0.0250 0.2387 0.1047 0.9166 -0.4429 0.4929
# Breedmixed -3.0163 2.1190 -1.4235 0.1546 -7.1695 1.1369
# BreedSiamese -3.1782 2.2048 -1.4414 0.1495 -7.4996 1.1433
r_country <- rma(xi=Responders, ni=N, measure="PR", slab=Study,
mods= ~ Country, data=cat)
summary(r_country)
# Mixed-Effects Model (k = 29; tau^2 estimator: REML)
#
# logLik deviance AIC BIC AICc
# 10.7309 -21.4619 -1.4619 8.4954 22.9826
#
# tau^2 (estimated amount of residual heterogeneity): 0.0096 (SE = 0.0061)
# tau (square root of estimated tau^2 value): 0.0978
# I^2 (residual heterogeneity / unaccounted variability): 63.38%
# H^2 (unaccounted variability / sampling variability): 2.73
# R^2 (amount of heterogeneity accounted for): 38.23%
#
# Test for Residual Heterogeneity:
# QE(df = 20) = 67.8909, p-val < .0001
#
# Test of Moderators (coefficient(s) 2:9):
# QM(df = 8) = 19.6513, p-val = 0.0117
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# intrcpt 0.6581 0.0365 18.0326 <.0001 0.5866 0.7297
# CountryAustralia -0.1272 0.1059 -1.2006 0.2299 -0.3348 0.0804
# CountryBrazil -0.1022 0.1081 -0.9458 0.3442 -0.3141 0.1096
# CountryCanada 0.1673 0.1052 1.5902 0.1118 -0.0389 0.3734
# CountryGermany -0.0897 0.1074 -0.8352 0.4036 -0.3003 0.1208
# CountryJapan 0.1889 0.0695 2.7186 0.0066 0.0527 0.3250
# CountryMexico -0.1359 0.1108 -1.2265 0.2200 -0.3531 0.0813
# CountrySpain -0.1181 0.1102 -1.0724 0.2835 -0.3341 0.0978
# CountryUK 0.0662 0.1026 0.6453 0.5188 -0.1349 0.2673
r_year <- rma(xi=Responders, ni=N, measure="PR", slab=Study,
mods= ~ Year + Country, data=cat)
summary(r_year)
# Mixed-Effects Model (k = 29; tau^2 estimator: REML)
#
# logLik deviance AIC BIC AICc
# 9.8005 -19.6011 2.3989 12.7878 40.1132
#
# tau^2 (estimated amount of residual heterogeneity): 0.0104 (SE = 0.0068)
# tau (square root of estimated tau^2 value): 0.1022
# I^2 (residual heterogeneity / unaccounted variability): 60.97%
# H^2 (unaccounted variability / sampling variability): 2.56
# R^2 (amount of heterogeneity accounted for): 32.52%
#
# Test for Residual Heterogeneity:
# QE(df = 19) = 66.6594, p-val < .0001
#
# Test of Moderators (coefficient(s) 2:10):
# QM(df = 9) = 18.5649, p-val = 0.0292
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# intrcpt -0.6080 2.7891 -0.2180 0.8274 -6.0745 4.8585
# Year 0.0006 0.0014 0.4536 0.6501 -0.0021 0.0034
# CountryAustralia -0.1455 0.1184 -1.2286 0.2192 -0.3775 0.0866
# CountryBrazil -0.1205 0.1203 -1.0016 0.3165 -0.3563 0.1153
# CountryCanada 0.1490 0.1177 1.2656 0.2057 -0.0818 0.3797
# CountryGermany -0.1080 0.1197 -0.9021 0.3670 -0.3427 0.1267
# CountryJapan 0.1845 0.0728 2.5331 0.0113 0.0417 0.3272
# CountryMexico -0.1542 0.1228 -1.2559 0.2091 -0.3948 0.0864
# CountrySpain -0.1364 0.1222 -1.1165 0.2642 -0.3759 0.1031
# CountryUK 0.0491 0.1131 0.4339 0.6644 -0.1725 0.2706
## moderately informative Bayesian meta-analysis
## (bayesmeta doesn't support moderators/meta-regression, so estimate just mean/SD):
library(bayesmeta)
b <- bayesmeta(y = escalc(xi=Responders, ni=N, measure="PR", data=cat),
mu.prior.mean=0.5, mu.prior.sd=0.1); summary(b)
# ...marginal posterior summary:
# tau mu theta
# mode 0.12487373717 0.6583157958 0.6588646213
# median 0.13029833512 0.6573472098 0.6575484257
# mean 0.13317030042 0.6568159715 0.6568159715
# sd 0.02521684197 0.0295391439 0.1389217521
# 95% lower 0.08801259311 0.5980530543 0.3796963066
# 95% upper 0.18372308609 0.7145549723 0.9312941009
#
# (quoted intervals are shortest credibility intervals.)
#
# relative heterogeneity I^2 (posterior median): 0.9288449557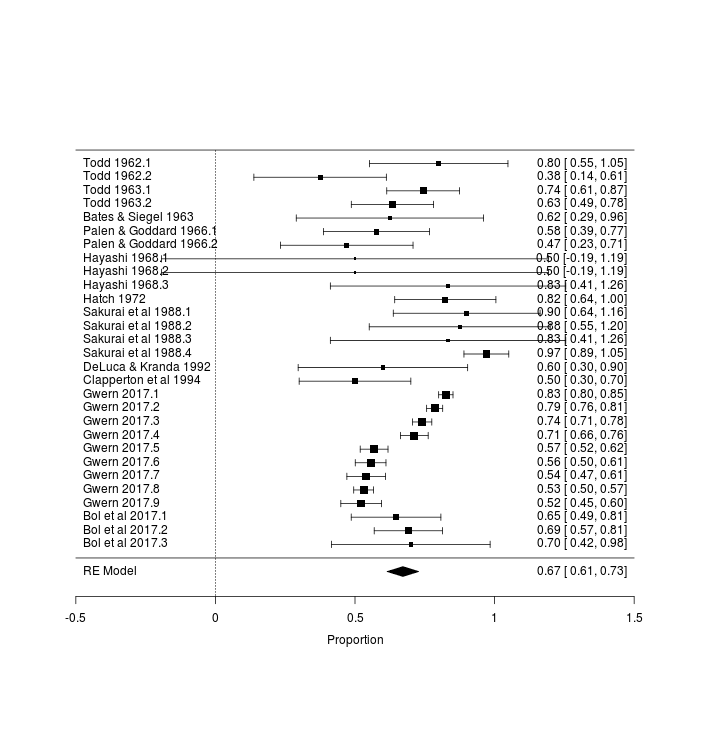
The 2⁄3 rule of thumb proves to be about right, with a meta-analytic summary of ~67% catnip response rates.
The heterogeneity of the results indicates that somethings are different from study to study or that biases like publication bias are at play; including the sex and breed covariates doesn’t help much because of the missing data, but there’s interesting trends of decreases with a study being conducted later in time.
The suspicious Sakurai 16⁄16 datapoint doesn’t show up in the full model because it has no sex information and gets dropped, so the Japanese trend there is being driven by the other Sakurai datapoints; the Hayashi results further support the Japanese anomaly. With additional data from my large-scale Google Surveys, the Japanese anomaly washes out: Japan does remain one of the highest catnip response country but looks much more reasonable, with a catnip response rate similar to Canada.
The decrease with time initially observed is odd in the full model, but it seems to be disappearing as additional studies are conducted, and it’s much more likely that it’s reflecting early differences in experimental procedure or breeds or countries than indicating that catnip response rates are being heavily selected against3, especially as the decrease with time disappears entirely if I ensure the 2017 surveys are included (rather than dropped for lack of sex/breed information).
Overall, the data quality is low as many authors (especially the early chemists) did not report individual response rates or key details of the cats used such as their age, breed, or sex, which is particularly unfortunate as all the samples are small enough that the original data could’ve been easily included as short tables. This is ironic because while some authors claim that sex/breed doesn’t matter at all, others claim that females react much more strongly (or was it males?), and yet most don’t report the data down by those variables, so their results can’t be pooled for an answer.
Cross-Species Catnip Response Rates
Catnip has been tested in a number of species. It would be interesting to include this data for several reasons: it can help the search for the genetic basis by comparing catnip-sensitive species with non-sensitive looking for genetic variants peculiar to the former, or if there is no apparent cluster of closely-related species which uniquely have catnip responses, it can test theories about what local environments might cause catnip sensitivity; it can potentially help sharpen estimates of sex/age/country/experimenter effects by ‘borrowing strength’; zookeepers can enrich their animals’ lives with catnip if they know which species respond; and since the data is already there in the papers, we might as well include it.
To examine cross-species trends, we would like to fit a multilevel model using family/genus/species, since one would expect the catnip response rate to be more similar between, say, African lions & tigers than between snow leopards & hyenas. Since each species might have different gender effects and population bottlenecks, we would ideally nest in each species the sex/country/breed/year covariates. We would also like independent random-effects for each study to allow for the heterogeneity we observed before (which could be independent of the family/genus/species hierarchy, in which case it would model things like different experimental procedures - eg. catnip leaves vs extract, or the experimenter being good or bad with animals - or it could be species-specific too). Unfortunately, such a full model would require estimating a huge number of parameters (with 24 species, 14 genuses, & 6 families, 10 studies, and 4 variables for each species, that’s easily 270 parameters which must be fit) and there is too little data (and the available data is compromised by the frequent missingness of species and sex), so we have to settle for something more modest, focusing on just the cross-species aspect.
## full model is unidentifiable due to too few data points and missingness:
# b <- bglmer(cbind(Responders, N) ~ (Sex+Country+Breed+Year|Species/Genus/Family) + (1|Study), family="binomial", data=catnip)
library(metafor)
# levels(catnip$Name) <- c(levels(catnip$Name), as.character(catnip[is.na(catnip$Name),]$Genus))
# catnip[is.na(catnip$Name),]$Name <- as.character(catnip[is.na(catnip$Name),]$Genus)
## sort by taxonomy:
catnip <- catnip[with(catnip, order(Family, Genus, Species)),]
catnip$Label <- with(catnip, Map(function(f,g,s, n) { paste0(n, " (", paste(f, g, s), ")") }, Family, Genus, Species, Name))
cross <- rma(xi=Responders, ni=N, measure="PR", slab=Label,
mods = ~ Species, data=catnip)
summary(cross)
# Mixed-Effects Model (k = 79; tau^2 estimator: REML)
#
# logLik deviance AIC BIC AICc
# 18.1500 -36.2999 23.7001 81.0608 121.5948
#
# tau^2 (estimated amount of residual heterogeneity): 0.0130 (SE = 0.0048)
# tau (square root of estimated tau^2 value): 0.1141
# I^2 (residual heterogeneity / unaccounted variability): 85.31%
# H^2 (unaccounted variability / sampling variability): 6.81
# R^2 (amount of heterogeneity accounted for): 73.68%
#
# Test for Residual Heterogeneity:
# QE(df = 50) = 399.0507, p-val < .0001
#
# Test of Moderators (coefficient(s) 2:29):
# QM(df = 28) = 114.5476, p-val < .0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# intrcpt 0.2500 0.3267 0.7651 0.4442 -0.3904 0.8904
# Speciesbengalensis 0.0000 0.4621 0.0000 1.0000 -0.9057 0.9057
# Speciescatus 0.4215 0.3279 1.2857 0.1986 -0.2211 1.0641
# Specieschaus 0.0000 0.4621 0.0000 1.0000 -0.9057 0.9057
# Speciesconcolor -0.0429 0.3422 -0.1253 0.9003 -0.7135 0.6278
# Speciescuniculus -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Speciesjubatus -0.1250 0.3836 -0.3259 0.7445 -0.8768 0.6268
# Speciesleo 0.6381 0.3350 1.9048 0.0568 -0.0185 1.2946
# Speciesleo/tigris 0.0000 0.4621 0.0000 1.0000 -0.9057 0.9057
# Specieslupus -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Specieslynx 0.5000 0.4621 1.0820 0.2792 -0.4057 1.4057
# Speciesmanul 0.0000 0.4621 0.0000 1.0000 -0.9057 0.9057
# Speciesmusculus -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Speciesnebulosa 0.2500 0.4947 0.5053 0.6133 -0.7197 1.2197
# Speciesnorvegicus -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Speciesonca 0.5767 0.3470 1.6618 0.0966 -0.1035 1.2568
# Speciespajeros 0.0000 0.4621 0.0000 1.0000 -0.9057 0.9057
# Speciespardalis 0.5500 0.3896 1.4118 0.1580 -0.2136 1.3136
# Speciespardus 0.4446 0.3436 1.2938 0.1957 -0.2289 1.1181
# Speciesporcellus -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Speciesrufus 0.1837 0.3675 0.5000 0.6171 -0.5365 0.9040
# Speciesserval -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Speciestemmincki 0.5000 0.4621 1.0820 0.2792 -0.4057 1.4057
# Speciestigris 0.0438 0.3471 0.1261 0.8996 -0.6366 0.7241
# Speciestigrus -0.1069 0.3431 -0.3115 0.7554 -0.7794 0.5656
# Speciesuncia 0.5833 0.3693 1.5794 0.1143 -0.1406 1.3072
# Speciesviverrina -0.0833 0.4075 -0.2045 0.8380 -0.8821 0.7154
# Specieswiedii 0.4167 0.3960 1.0522 0.2927 -0.3595 1.1928
# Speciesyagouaroundi -0.1500 0.3712 -0.4041 0.6861 -0.8775 0.5775
png(file="~/wiki/doc/cat/psychology/drug/catnip/gwern-catnip-forest-crossspecies.png", width = 580, height = 1600)
forest(cross)
invisible(dev.off())
library(blme)
b <- bglmer(cbind(Responders, N) ~ (1|Species/Genus/Family) + (1|Study) + Year, family="binomial", data=catnip)
summary(b); ranef(b)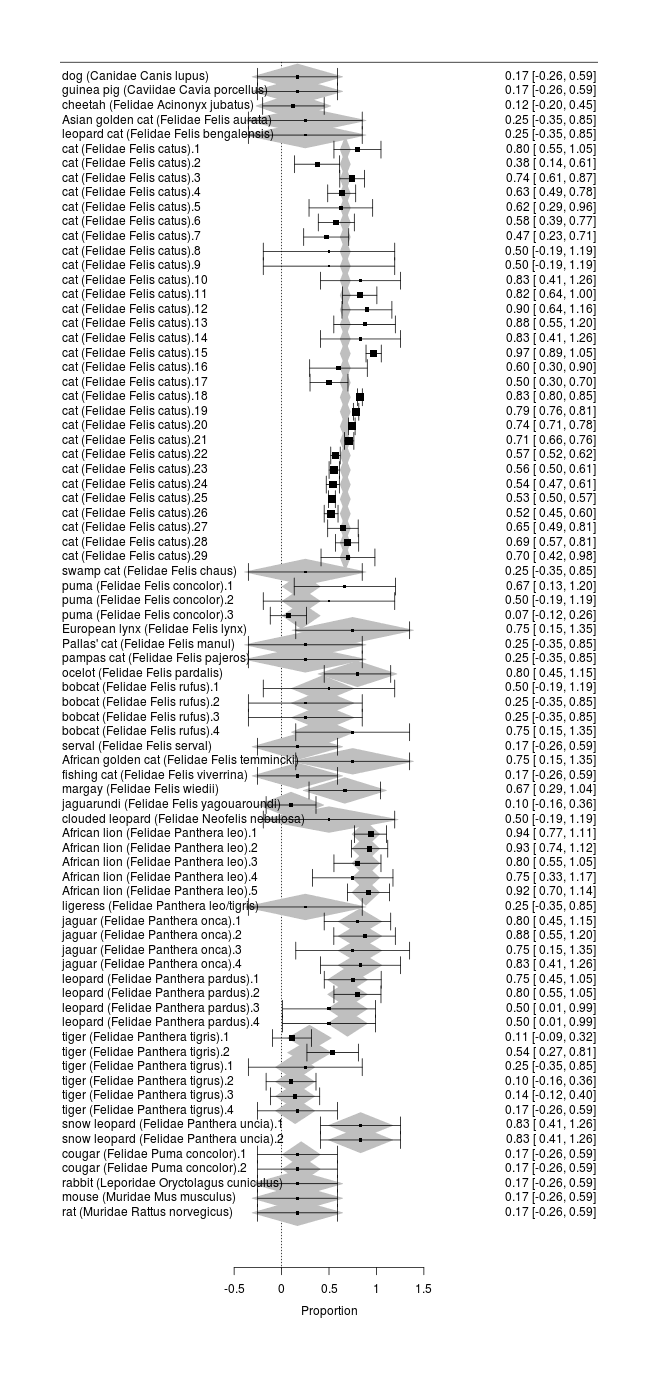
Surveys
Main article: World Catnip Surveys.{.include-annotation .backlink-not}
Optimal Catnip Alternative Selection: Solving the MDP
et al 2017 tested 4 cat stimulants on a large (n > 100) sample of cats, yielding within-individual correlations of stimulant responses. This allows prediction of stimulant response conditional on observing other stimulant responses. I use this to demonstrate how to optimize stimulant selection as a sequential testing problem, yielding (for one set of realistic purchase costs) a test sequence of catnip → honeysuckle → silvervine → Valerian, which is different from the greedy policy of picking stimulants by prior probability.
et al 2017, as noted, provides responses for 4 drugs (catnip/Valerian/silvervine/honeysuckle) in a large sample of cats; responses turn out to be heavily intercorrelated, permitting the ability to better predict responses to the catnip alternatives based on a known response to one of the others. This becomes useful if we treat it as a drug selection problem where we would like to find at least one working drug for a cat while saving money, and adapting our next test based on failed previous tests.
If they were not intercorrelated, one would simply minimize expected loss in a greedy fashion, starting with catnip etc; but as they are intercorrelated, now a drug has both direct value (if the cat responds) and value of information (its failure gives evidence about what other drugs that cat might respond to), which means the greedy policy may no longer be the optimal policy. The optimal sequence can be derived by considering all possible sequences of tests, updating predictions in a Bayesian fashion for each hypothetical sequence, calculating total expected losses based on the posterior probabilities, and minimizing losses. For one set of costs and one cat response dataset, I derive an optimal sequence of: catnip, honeysuckle, silvervine, and valerian. Implementation below.
Load et al 2017 for predicting response to one drug based on responses to others:
bol2017 <- read.csv("https://gwern.net/doc/cat/psychology/drug/catnip/2017-bol-cats.csv")
bol2017[,5:8] <- (bol2017[,5:8] > 0) # treat '5'/'10' (weak/strong response) as binary
bol2017Responses <- subset(bol2017, select=c("Catnip", "Valerian", "Silver.vine", "Tatarian.honeysuckle"))
colnames(bol2017Responses) <- c("Catnip", "Valerian", "Silvervine", "Honeysuckle") # rename for consistency
library(skimr)
skim(bol2017Responses)
#... variable missing complete n mean count
# Catnip 1 99 100 0.68 TRU: 67, FAL: 32, NA: 1
# Honeysuckle 3 97 100 0.53 TRU: 51, FAL: 46, NA: 3
# Silvervine 0 100 100 0.79 TRU: 79, FAL: 21, NA: 0
# Valerian 4 96 100 0.47 FAL: 51, TRU: 45, NA: 4
library(psych)
tetrachoric(bol2017Responses)
# tetrachoric correlation
# Catnp Valrn Slvrv Hnysc
# Catnip 1.00
# Valerian 0.60 1.00
# Silvervine 0.24 0.47 1.00
# Honeysuckle 0.43 0.35 0.23 1.00
#
# with tau of
# Catnip Valerian Silvervine Honeysuckle
# -0.459 0.078 -0.806 -0.065Greedy one-step policy + simple marginal probability chooses a test sequence of catnip/valerian/silvervine/honeysuckle:
|
Drug |
Cost |
P |
Loss |
|---|---|---|---|
|
Catnip |
8.96 |
0.67 |
2.9568 |
|
Valerian |
7.00 |
0.47 |
3.7100 |
|
Silvervine |
17.77 |
0.79 |
3.7317 |
|
Honeysuckle |
7.99 |
0.53 |
3.7553 |
costs <- read.csv(stdin(), header=TRUE, colClasses=c("character", "numeric"))
Drug,Loss
Catnip,8.96
Valerian,7.00
Silvervine,17.77
Honeysuckle,7.99Define a catnip testing MDP: we are testing 4 cat drugs with intercorrelated responses, we want to find 1 drug which works, and we want to minimize the monetary loss (since we have to pay for each one as defined above). What is the optimal sequence, which minimizes expected loss before finding 1 working drug? We can solve by backwards induction on a decision tree and using Bayesian linear regression to predict posterior probability of each remaining drug’s success probability conditional on previous drugs not working (rather than using just the unconditional, marginal, probability of any cat responding to each):
library(rstanarm)
library(memoise)
library(boot)
predictBayes <- memoize(function (action, observations, df) {
formula <- as.formula(paste(action, paste(c(names(observations), "1"), collapse=" + "), sep=" ~ "))
b <- stan_glm(formula, family=binomial(), algorithm="optimizing", data=bol2017Responses)
print(b)
if (length(observations)==0) { mean(inv.logit(predict(b))) } else { inv.logit(predict(b, newdata=as.data.frame(observations))[1]) } })
f <- memoize(function(observations) {
allActions <- colnames(bol2017Responses)
actions <- allActions[!allActions %in% (names(observations))] # untried drugs
if (length(actions) == 0) { return(0) } else {
actionCosts <- costs[costs$Drug %in% actions,]$Loss
probabilities <- c(numeric())
for (i in 1:length(actions)) {
probabilities[i] <- predictBayes(actions[i], observations, bol2017Responses)
}
lossActions <- c(numeric())
for (i in 1:length(actions)) {
# we pay the loss to test each action; if successful, we stop here, otherwise we add a FALSE observation and recurse
obs <- list(a=FALSE); names(obs) <- actions[i]
obs <- c(observations, obs)
newHistory <- obs[order(unlist(obs), decreasing = TRUE)] # sort history to avoid unnecessarily different but equivalent calls
# 1. incur cost of each drug; success means stopping; failure: augment history with failure observation, and look for an optimal path through remaining actions recursively by calling 'f' again
lossActions[i] <- actionCosts[i] + probabilities[i]*0 + ((1-probabilities[i]) * (f(newHistory)))
}
print(data.frame(Actions=actions, P=probabilities, Loss=lossActions))
print(paste("Optimal action: ", actions[which.min(lossActions)], "; given observations: ", names(observations), observations))
return(min(lossActions)) }
})
# f(list(Catnip=FALSE, Honeysuckle=FALSE, Silvervine=FALSE))
f(list())
## No data, optimal choice is catnip:
# Actions P Loss
# 1 Catnip 0.6810641502 15.79007271
# 2 Valerian 0.4731509696 16.92706363
# 3 Silvervine 0.7879218896 20.92153367
# 4 Honeysuckle 0.5276423201 16.51408849
## With catnip resistance, optimal choice is honeysuckle:
#
# Actions P Loss
# 1 Valerian 0.2005122547 23.27730700
# 2 Silvervine 0.7202520977 21.49101933
# 3 Honeysuckle 0.3287608075 21.41519278
## With catnip/honeysuckle resistance, optimal choice is silvervine, and if silvervine doesn't work, only Valerian is left:
#
# Actions P Loss
# 1 Valerian 0.1695397115 21.75727933
# 2 Silvervine 0.6813415396 20.00060922
## Final optimal policy: catnip, honeysuckle, silvervine, Valerian; aside from catnip, almost reverse of greedy policy.Known Cat Stimulants


“Catnip, Valerian, Honeysuckle and other cat-attractant plants”, 2008:
-
Nepeta cataria (catnip): active ingredient nepetalactone
-
Lonicera Tatarica (Tatarian Honeysuckle) https://en.wikipedia.org/wiki/Lonicera_tatarica : nepetalactone TODO: that can’t be the only ingredient if catnip doesn’t work on Percy and honeysuckle does?
-
Valerian:
-
Valerian officinalis https://en.wikipedia.org/wiki/Valerian_%28herb%29#Effect_on_other_organisms : active ingredient actinidine
-
Valeriana celtica https://en.wikipedia.org/wiki/Valeriana_celtica : active ingredients nepetalactone ( et al 1983)
-
-
Actinidia Polygama (Japanese Catnip or Matatabi or Silvervine or silver vine or cat powder) https://en.wikipedia.org/wiki/Actinidia_polygama#Pets and Actinidia macrosperma : active ingredient Actinidine and dihydroactinidiolide
-
1968 claims to have found no responses in an unspecified but probably >4 number of cats when testing nepetalactone (catnip) and actinidine solutions, aside from two actinidine reactions: salivation when poured into one cat’s mouth and vomiting after an injection. Oddly, Hayashi claims in the conclusion section “Our experiments do not support the claim that Actinidia palygama produces behavioural changes in cats” and then immediately following that in the summary section that “The actinidine reflexes, called forth by the odour of the fluid, were observed in cats but not in mice, rabbits or guinea pigs.”, so I am left confused about what Hayashi’s results were.
-
et al 1998 notes that their cultured fruit calluses would “produce only a low amount of attractant for cats”, so wood/leaf is probably necessary for a response
-
et al 1960a, “Chemical components in matatabi. I. The isolation of the physiologically active principles, matatabilactone and actinidine” [in Japanese]
-
et al 1969, “Biologically active C9-, C10-, and C11-terpenes from Actinidia polygama, Boschniakia rossica, and Menyanthes trifoliata” (in Japanese; Tucker & Tucker summary: “ et al 1969 also isolated onikulactone from B. rossica and found that it induced the catnip response in cats.” None of the Sakan papers in English mention behavioral data or experiments, just chemistry.)
-
Hazama N (1942) “Felidae species and Actinidia polygama”. Shizen [‘Nature’] 6:55-59 [in Japanese]
A “Hazama, N” is mentioned several times in The Monkeys of Arashiyama: Thirty-five Years of Research in Japan and the West as one of the first researchers to study those monkeys, so apparently he was a biologist of some sort, but is listed as deceased as of 1991. The bibliography includes a 1962 publication in “Iwatayama Shizen Kenkyujo Chosa Kenkyu Hokoku” but it’s cited as volume 1, so can’t be the ‘Shizen’ in question. Folia psychiatrica et neurologica japonica, Volumes 17-18 1963 cites Hazama twice:
-
Hazama, N: Felidae and Matatabi. Shizen (Nature), 6: 55-59, 1951 (Japanese)
-
Hazama, N: Cat and Matatabi. Iden (Heredity), 7: 33-37, 1953 (Japanese)
So the original citation to 1942 may be wrong or he may’ve published three almost identically-titled papers (“Matatabi” = “Actinidia polygama”).
-
-
-
Acalypha indica (Indian acalypha/Indian nettle), active ingredients: Isodihydronepetalactone, Isoiridomyrmecin (eg. et al 2016)
-
cat thyme (teucrium marum) : active ingredient TODO
-
Buckbean (Menyanthes trifoliata): mitsugashiwalactone
-
Northern groundcone (Boschniakia rossica): boschniakine and boschnialactone
-
Yellowbells (Tecoma stans): boschniakine and actinidine
-
Trumpet Creeper (Campsis radicans): may boschniakine
-
Guelder Rose (Viburnum opulus, sometimes called Cranberry Bush and most commonly found in cultivation as the Snowball Tree)
-
the perennial Dittany of Crete (Origanum dictamnus/Hop Marjoram)
-
the spring-flowering annual Baby Blue-eyes (Nemophila menziesii)
-
the Zimbabwean plant Zinziba (Lippia javanica aka Verbena javanica).
Speculative:
-
there are anecdotal reports that some cats are attracted to olive products: olive wood, olive oil, and olive fruits themselves
Local Cat Experiments
The catnip literature has a good sample of what the catnip frequency response is, but it’s clear that a lot of cats are immune and their owners need to use one of the many substitutes. The literature does not seem to have much, if any, coverage of all the main alternatives, so owners don’t know what to try after catnip. There’s also no information on any correlations between responses: does catnip immunity cause susceptibility to a different stimulant? Are some cats more response to stimulants in general? If we know a cat is immune to, say, catnip and valerian, can we better predict what an owner should try next?
Since cats are easy to come by and the stimulants are cheap, I thought it might be interesting to assemble a collection of stimulants and systematically try them out on each cat I should happen to meet. Specifically, I’ll look at the most common and easy to come by stimulants, since it’s not useful to discover that some extinct African flower is super-potent:
-
Catnip (obviously)
-
Tatarian honeysuckle (one of the most frequently mentioned alternatives)
-
Valerian (not as commonly mentioned, but very cheap due to its popularity as a herbal supplement for sleep & anxiety)
-
Silvervine (rarer & more expensive but still accessible, and reputedly quite effective)
-
Cat thyme
-
Olive oil/wood (cats’ reacting to olive-related things is an obscure & anecdotal claim; but both are easy to get and included for the sake of comprehensiveness)
Purchasing
-
Stimulants:
-
I Love Catnip! 2 oz Liquid Catnip Spray, by Pet MasterMind: $11.62$8.962015
-
Honeysuckle Spray for Cats (2 oz): $10.36$7.992015
-
Valerian Root Extract: $15.38$11.862015 (another possibility: Nature’s Answer super-concentrated 1 fluid oz, $9.08$72015)
-
Arata Silvervine 12x0.5g, Cat’s Favorite, Best Value: $14.2$10.952015 + $8.84$6.822015 (S&H from Japan for the silvervine) = $23.05$17.772015 or $3.84$2.962015/g (ordered 2015-11-08, arrived 2015-12-04); silvervine is also available for less as Vitakraft Purrk Playful Toys for Silvervine Refills with Mouse, 5-Pack, $5.82$4.492015 for 5x0.5g or $2.33$1.82015/g, and I am using this as well. (The Arata silvervine powder is a gray tan, while the Vitakraft looks more like an brown/orange tan. I do not know if this color difference reflects a difference in potency due to freshness or concentration or varietal.)
-
olives:
-
Titone Bio Organic Extra Virgin Olive Oil 2015: $49.22$37.952015
Normally I would not buy such extremely expensive artisanal olive oil as regular virgin olive oil is adequate for my cooking, but the olive oil trade is notoriously rife with counterfeits and tests with standard supermarket wares might be worse than useless if I am actually testing out soy/hazelnut/sunflower-seed/canola oil and they turn out to not have any of the critical cat-attractant chemicals. The 2015 oil is recent and this brand should be authentic. (If nothing else, it tastes quite good.)
-
Large Olive Wood Pen Blanks from Bethlehem - 15.5 × 3.8 × 3.8 cm (6.1 × 1.496 × 1.496 Inch): $12.44$9.592015
Cheapest unworked/unprocessed chunk of olive wood I could find on Amazon.
-
-
Cat thyme/Teucrium marum potted plant from Companion Plants: $21.26$172016 (initial exposure for my cat & Percy: neither especially reacted but Percy sniffed it substantially longer. The plant does not smell strongly to me and seems a bit out of sorts, so perhaps it is simply in bad condition and at the end of the season. It unfortunately died over a winter and I had to buy a second one in 2018.) Photos of my planter with catnip & cat thyme growing: front/side/from above.
-
subtotal: $111.12
-
-
Toys (need multiple to avoid cross-contamination):
-
Go Cat Teaser Cat Catcher Wand Cat Toy: $9.12$7.032015
-
ColorPet Bird Replacement Feathers and Soft Furry For Interactive Cat and Kitten Toy Wands Super Refill, Assorted Colors Cat Toys; 9 pieces: $12.48$9.622015
-
subtotal: $21.59$16.652015
-
-
total: $82$63.232015
For each stimulant, one clean never-used feather was put into a clean jar along with a good helping of the relevant stimulant, and shaken and left to sit. The olive wood would not fit into a jar, so I sawed it in half, saved the sawdust, and put the two wood blocks, sawdust, and feather into a little ziplock bag. The wand lets the feathers be added or removed easily so I can test each feather one at a time by switching feathers, playing with the cat for 5 minutes, and waiting for any response or indication of interest beyond regular chase. This works well, aside from the silvervine powder where inevitably some of the powder falls off or blows out of the container, so it’s best to do the silvervine last.
Efficacy
|
Cat |
Sex |
Age |
Fixed |
Color |
Kind |
Catnip |
Valerian |
Honeysuckle |
Silvervine |
Olive wood |
Olive oil |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
My cat |
M |
1.5 |
1 |
black |
Domestic long |
0 |
1 |
0 |
1 |
0 |
0 |
|
Percy |
M |
3 |
1 |
brown |
Tabby |
0 |
0 |
1 |
1 |
0 |
0 |
|
Kiki |
M |
2 |
1 |
grey |
Tabby |
1 |
|||||
|
Stormy |
M |
10 |
1 |
grey |
Russian Blue |
||||||
|
Sara |
F |
10 |
1 |
brown |
Tabby |
1 |
|||||
|
Whitey |
F |
5 |
1 |
white |
Domestic short |
1 |
|||||
|
Sassy |
F |
12 |
1 |
orange |
Domestic short |
0 |
0 |
0 |
1 |
0 |
0 |
Description of effects:
-
Catnip: too well known to need much description. Catnip responder cats become ‘hyper’, uninhibited, playful, interested in the catnip toy.
Testing it in my 2 non-responder cats in December 2014, Percy and my cat initially sniffed it for a few seconds and then ignored it afterwards, regardless of whether I shook a quarter kilogram of catnip leaf under their nose or let the open jar sit next to them. Likewise, attempts to interest them in the catnip extract spray in November 2015 also failed. In October 2016, I purchased ~100g of dried catnip leaves at a local Renaissance festival to have a backup for the catnip extract spray and perhaps try out “catnip tea” myself (and if I can’t find any use for it, I can always experiment with home steam distillation of catnip oil from catnip leaves!). Retesting Percy/my cat with the new leaves, Percy remained uninterested but this time my cat was interested in the plastic bag containing the catnip leaves, trying to claw and chew it, so I put ~10g into a little cotton bag and give it to him, which he began to chew and claw and even laid down to hold it in his paws and kick at it - however, despite resembling the catnip response, he was not hyper, and he did not repeat the reaction on 4 subsequent occasions I tried to interest him in the catnip bag (spraying it with the catnip extract did not help). This makes me wonder if catnip response might have some ultra-long tolerance like some drugs in humans which take weeks or months for tolerance to be restored, or if the catnip response is not bimodal after all (catnip being an dominant gene would certainly seem like it almost has to produce a bimodal/binary trait, but we have only 1962 as evidence for it being dominant, and he used a single small breeding colony and no one has ever followed up & tried to replicate it that I know of). Perhaps the issue of measurement error has been underestimated in past studies and many cats will only display a catnip response occasionally or under ideal conditions, and so the estimates of catnip immunity are heavily biased upwards?
-
Valerian: on my cat, produces an interesting mix of passiveness and possessiveness - after onset and a long Flehmen response, he mostly lays on the floor passively, occasionally pulling himself across it towards the toy, but generally making little effort to hunt; if the toy comes within reach, though, then he seizes it energetically and abruptly begins clasping it to his face, chewing it, curling up around it and kicking at the toy with his hind legs. Eventually he can be coaxed into playing chase normally, with his usual level of competence and interest. Actively repelled Sassy.
-
Honeysuckle: on Percy, had a general stimulant effect; despite being fat, lazy, and usually entirely uninterested in chase, he will make an effort to play after sniffing a honeysuckle-impregnated toy. This stimulating effect does not produce the un-inhibition of catnip, and seems fairly mild. Actively repelled Sassy.
-
Silvervine:
-
on my cat, a general stimulating effect with considerable interest in playing chase or watching the toy, but curiously, he makes many fewer attempts at attacking or chasing and when he does, he is distinctly slower (and thus, less effective) than usual. His coordination is fine - he’s not clumsy or falling over - but he’s just not as effective (in a way hard to pin down specifically).
-
On Percy, likewise a general stimulating effect but far more effective than the honeysuckle in inducing chase play, with him even trying out jumps when coaxed appropriately; he may be less effective, like my cat when affected, but he plays chase so little that it’s impossible for me to make any comparisons with his ‘normal’ chase behavior.
-
Sassy: similar. More time on back while playing chase than usual.
-
-
Olive oil/wood: all cats showed brief interest in smell, then ignored entirely.
External Links
-
Discussion: HN
Appendix
Breeding Cats To Increase Frequency Of Catnip Response
I sketch out a threshold selection breeding program for increasing catnip response frequency. Based on 2011’s measured heritabilities of catnip response (corrected for measurement error), selecting exclusively responders would result in catnip response becoming nearly universal (~95%) within ~7 generations or potentially less than a decade.
Given the benefits of catnip for behavioral enrichment, it’s unfortunate that cat breeders have not used a little selection pressure to make catnip response universal. There are 3 major scenarios for catnip breeding, depending on the genetic architecture of catnip response (which remains in some doubt):
-
Mendelian autosomal dominant: marker-assisted genetic selection: 1 generation to fixation
A genetic test for catnip response is not available as of July 2017, since the allele has not even been localized to any chromosomes, much less identified, and given the small niche of cat genetics research, large-scale GWAS would almost certainly be very expensive (eg. the 99 Lives Cat Genome Sequencing Initiative requires, as of July 2017, ~$8524.28$70002017 to sequence 1 cat genome, which is >7x more than it would cost to sequence a human genome via Veritas, and they have sequenced 53 cats, increasing to 131 by February 2019 as their 30x WGS cost has apparently dropped to ~$1500; to sequence “Lil Bub”, et al 2019 targeted $8429.89$65002015 in May 2015). As catnip response appears somewhat similar across the felids, a successful find of a catnip gene in another species might make it much easier to find it in cats, reducing the sample size requirement.
Fortunately, cats are otherwise not expensive to test, as a number of successful existing feline saliva-based genetic tests indicate (2009, 2010, 2012): as of August 2017, the UC Davis Veterinary Genetics Laboratory offers coat color, ancestry, parentage, blood group, genetic diseases (Progressive Retinal Atrophy/PRA-PK Deficiency, Glycogen Storage Disease Type IV, GM1 & GM2 Korat Gangliosidosis, Polycystic Kidney Disease etc) for prices ranging $48.71$402017–$146.13$1202017; the UK Langford Vets (University of Bristol) offers a similar list of tests starting at £36.60/$48; the US CFA’s CatDNAtest.org offers a more limited selection but again all for $45. The Morris Animal Foundation sponsored development of an Illumina feline SNP array (the “Illumina Infinium iSelect 63K Cat DNA Array”) starting around 2011 (with unfortunately a limited selection of only 70k SNPs as opposed to the 500k+ standard in human SNP arrays), and as of 2014, was offering it for$100 to researchers. Hence, it is plausible that after discovering the catnip allele, the cost of testing a single cat might be <$60.89$502017.
Once a genetic test does become available at sufficiently low cost, it offers by far the fastest and most powerful selection method. Given a genetic test for the catnip allele (as a common variant, it is likely easily tested for), breeding could be conducted in 1 generation: test the population of catnip responders, and breed only the homozygous dominant cats (ie. the cats with 2 copies), who make will make up ~0.442 = 19% of the population. All offspring will then also be homozygous dominant & thus catnip responders, and catnip response rates will be 100% barring any further introduction from outside the breeding population of recessive carriers. This sort of single-generation selection would be doable at fairly modest total cost, <$121775.38$1000002017 (eg. start with 1000 cats, test for catnip response; about half will respond, and testing each at $60.89$502017 would cost ~$30443.85$250002017, of which about half will be homozygous rather than heterozygous, giving a large founding population of ~250 cats all of whose descendants will be catnip responders).
-
Mendelian autosomal dominant: phenotypic selection: ~9 generations to near-universality (>=99%)
Assuming there is no genetic test, one can instead breed based on the observed phenotype of catnip response; this will be slower and less efficient because heterozygous and homozygous cannot be distinguished.
But if Todd is correct about the allele being dominant, catnip response is still easily bred, since selection against a recessive proceeds fast when starting from a high frequency. Under the Mendelian autosomal dominant theory, if the catnip recessive is present at q = 0.56 per 1962, and we would like to decrease the rate of catnip resistance in a breed to <=1%, then we need to decrease the frequency to √0.01 = 0.10. If we breed only catnip responders (which fortunately are the majority already), this corresponds to a selection intensity s=1, and the number of generations has the simple equation (more general treatments: 1, 2) n = 1⁄qn − 1⁄q0 or 1⁄√0.01 − 1/0.56 = 8.2 generations. Cats mature reproductively at 18 months & pregnancy is around 2 months, so 8.2 generations would take ~14 years (((18+2) × 8.2) / 12). So a phenotypic catnip breeding program need not take an infeasible amount of time based on 1962’s estimates.
-
polygenic liability-threshold: phenotypic selection: ~25 generations to near-universality
Alternatively, if Todd is incorrect about catnip being Mendelian dominant controlled trait, it still appears to run in families & species and thus have a genetic basis, so, since the trait appears binary, the true genetic architecture might then be a liability threshold trait. Phenotypic selection in the liability threshold trait depends on the population frequency of the trait (which defines the unobserved latent threshold’s starting point, and efficacy slows at the extremes of 0 and 1) and on the heritability of the trait (which defines the genetic response to each generation of selection; unfortunately, unknown for cats). Large-scale human twin studies such as et al 2015 turn in a grand mean across all studied human traits of ~50% heritability, and the largest multi-behavioral-trait cat heritability study I know of, et al 2019, likewise obtains tight estimates of 50–50% heritability, so a priori one would expect a reasonably high heritability, and 2011’s large catnip results indicate, considering the measurement error, a heritability of at least 0.7, so we will consider that scenario:
threshold_select <- function(fraction_0, heritability) { fraction_probit_0 = qnorm(fraction_0) ## threshold for not manifesting schizophrenia: s_0 = dnorm(fraction_probit_0) / fraction_0 ## new rate of schizophrenia after one selection where 100% of schizophrenics never reproduce: fraction_probit_1 = fraction_probit_0 + heritability * s_0 fraction_1 = pnorm(fraction_probit_1) ## how much did we reduce schizophrenia in percentage terms? print(paste0("Start: population fraction: ", fraction_0, "; liability threshold: ", fraction_probit_0, "; Selection intensity: ", s_0)) print(paste0("End: liability threshold: ", fraction_probit_1, "; population fraction: ", fraction_1, "; Total population reduction: ", fraction_0 - fraction_1, "; Percentage reduction: ", (1-((1-fraction_1) / (1-fraction_0)))*100)) return(fraction_1) } heritability <- 0.70; frac <- 0.61 threshold_select(frac, heritability) # ... # [1] 0.7641164429 generations <- 0; while (frac < 0.99) { frac <- threshold_select(frac, heritability); generations <- generations+1 } # ... generations # [1] 25Progress, while initially swift (eg. getting to 95% only takes ~7 generations), slows down rapidly towards the target of 99% response rates. The selection, especially towards the end, could be improved by taking into account genetic information such as pedigree or GWAS-based polygenic scores in order to select against cats with a high liability for catnip resistance but who do not display the phenotype; modeling that, however, would be difficult without more data.
-
For example, 1962’s genetic analysis was based on just 34 cats of which 7 cats’ response were unknown; as far as I can tell, another pedigree analysis has never been done since then, much less extended to newer genetic methods like linkage or GWASes, although it continues to be cited as the justification for treating catnip response as an autosomal dominant genetic trait.↩︎
-
An example of founder effects in cat populations are the feral cats of Kerguelen Islands, whose fur colors are >95% black (or black with white spots): 1970, 1971, 1974, 1994, et al 2004 ↩︎
-
If catnip sensitivity frequency was 70% in 1950, and for the sake of argument we accepted that the proportion had decreased ~0.0024 per year and was 54.16% in 2016, and we also accept 1962’s analysis that catnip sensitivity is a dominant gene, then that implies that the frequency of the gene in 1950 was 0.7 = p2 + 2pq and so in 1950 p = 0.45; similarly, 0.516 = p2 + 2pq, and so in 2016 p = 0.30, so the gene frequency would’ve fallen by 0.15 1950 → 2016. If a domestic or wild cat generation is 3 years, then that 66 years is >22 cat generations, and dividing a total fall of 15% over that period, the gene frequency would be falling ~0.68% per generation.
While this could be caused by fairly weak selection against catnip responders, it’s hard to imagine what could cause that selection or how it is consistent with the continued existence of catnip responders given that: catnip has no known ill effects on cats, is rarely found in the wild, most cats are never exposed, those cats which are exposed at all tend to be pets which are spayed/neutered, no solid sex or breed correlation has been observed, and the existence of catnip responders has been documented for centuries (according to 1988, John Ray, died 1705, was the first, and Gary Lockhart attributes the first mention of cats/catnip to Al-Biruni, died 1048).↩︎