Bacopa Quasi-Experiment
A small 2014–2015 non-blinded self-experiment using Bacopa monnieri to investigate effect on memory/sleep/self-ratings in an ABABA design; no particular effects were found.
Bacopa is a supplement herb often used for memory or stress adaptation. Its chronic effects reportedly take many weeks to manifest, with no important acute effects.
Out of curiosity, I bought 2 bottles of Bacognize Bacopa pills and ran a non-randomized non-blinded ABABA quasi-self-experiment from June 201412ya to September 201511ya, measuring effects on my memory performance, sleep, and daily self-ratings of mood/productivity.
For analysis, a multi-level Bayesian model on two memory performance variables was used to extract per-day performance, factor analysis was used to extract a sleep index from 9 Zeo sleep variables, and the 3 endpoints were modeled as a multivariate Bayesian time-series regression with splines.
Because of the slow onset of chronic effects, small effective sample size, definite temporal trends probably unrelated to Bacopa, and noise in the variables, the results were as expected, ambiguous, and do not strongly support any correlation between Bacopa and memory/sleep/self-rating (+/−/− respectively).
Bacopa monnieri (Examine, nootropics survey (2020), Reddit discussions) is an herb prominent for its use in Ayurvedic medicine. Taken chronically over long time-periods, Bacopa may improve cognition and help with stress, but (like some other Ayurvedic remedies) has a potential drawback in the form of heavy metal contamination.
Background
The psychology & medical literature is sporadic and studies are somewhat uninterpretable due to variables of dosage & dose length, but overall the evidence for improvements is better than that for most nootropics. “The Cognitive-Enhancing Effects of Bacopa monnieri: A Systematic Review of Randomized, Controlled Human Clinical Trials” found evidence of benefits to memory in several >=12-week-long RCTs. “Cognitive effects of two nutraceuticals Ginseng and Bacopa benchmarked against modafinil: a review and comparison of effect sizes” reviewed mostly the same studies. “Meta-analysis of randomized controlled trials on cognitive effects of Bacopa monnieri extract” attempted to meta-analyze the studies (specifically: et al 2001b, et al 2002, et al 2006, et al 2008, et al 2008, et al 2008, Peth- et al 2012, & et al 2013) and found that of the 21 possible metrics/tests, the trail-making and reaction-time improvements had low heterogeneity between studies & also reached statistical-significance; unfortunately, heterogeneity was high in most metrics, few studies examined the same metrics, and the low study count renders impossible any estimate of how bad the publication bias is (typically severe) or other checks of quality/reliability, so the results are not as impressive as they might appear. Overall, it seems Bacopa likely has some useful effects.
Practically, I have 2 concerns about Bacopa:
obtaining a heavy-metal-free product for long-term consumption (what good is it to benefit from Bacopa if you are simultaneously building up a long-term heavy metal burden?)
CoAs are the first line of defense but availability differs: Ayur Sante, Nutrigold, Indigo Herbs, Banyan Botanical & Nutricargo reportedly provide CoAs as does NootropicsDepot; while Planetary Herbals, Himalaya, & Mind Nutrition have stonewalled requests.
Probably the best bet is to go with Bacognize: NootropicsDepot’s CoA & an independent lab test confirms that the heavy metal levels are acceptably low in that standardized branded source. (May cost more, though.)
how hard self-experimenting is.
Self-experimenting is both easy and hard: it’s easy because there should be effects on memory recall which can be easily extracted from spaced repetition software like Mnemosyne, but hard because onset requires many weeks so a self-experiment must either have few blocks (limiting comparability) or be lengthy (to allow for multiple transitions between Bacopa and placebo conditions). I may have to settle for a lesser analysis like a before-after comparison, and only then if the results are positive consider the expense & difficulty of a full RCT over a number of months.
Bacopa Sources
Bacopa can be bought from a number of retailers. There are several capsule sellers on Amazon, and NootropicsDepot sells both capsules & powder. More specifically (as of 2014-09-11, assuming using Amazon’s free shipping & NootropicsDepot’s regular S&H):
Seller |
Form |
Content/brand |
Dose (mg) |
Count |
Price ($) |
S&H |
mg/$ |
|---|---|---|---|---|---|---|---|
Cap |
Bacognize |
300 |
60 |
25.49 |
0 |
706 |
|
Cap |
Bacognize |
250 |
120 |
11.99 |
7.25 |
1159 |
|
Cap |
Bacognize |
300 |
60 |
8.99 |
4.49 |
1335 |
|
Cap |
Bacognize |
300 |
120 |
20.49 |
4.49 |
1441 |
|
Cap |
Bacognize |
250 |
240 |
22.99 |
7.25 |
1984 |
|
Cap |
Bacognize |
250 |
90 |
11.25 |
0 |
2000 |
|
Cap |
BacoMind+generic |
500 |
90 |
16.99 |
0 |
2649 |
|
Powder |
Bacognize |
125000 |
1 |
24.99 |
7.25 |
3877 |
|
Cap |
Bacognize |
300 |
240 |
12.49 |
4.99 |
41191 |
|
Powder |
Bacognize |
250000 |
1 |
45.99 |
7.25 |
4695 |
|
Powder |
Bacognize |
500000 |
1 |
89.99 |
7.25 |
5142 |
The cheapest Bacognize, if one doesn’t want to cap one’s own pills (as one probably does since the powder reportedly tastes bad), would seem to be the Swanson. (The Nutrigold is substantially cheaper, but also comes with a different branded source and is half-generic, and if one wanted to roll the dice, there are probably much cheaper sources of Bacopa on Amazon.) At 90x250mg, the dose per pill is a little inconveniently low for daily usage (>=300mg would be better) but still usable, so the daily cost would be $0.13, and it’d cover 90 days - conveniently, the same time period used in a number of studies such as et al 2008.
Quasi-Experiment
Intervention
I ordered 2 bottles of the Swanson on 14 September, and began taking one pill in the morning with olive oil on 2014-09-26. I decided to do an ABABA trial (baseline/Bacopa/off/Bacopa/off), checking for correlated changes in my Mnemosyne spaced repetition memory scores/grades, Zeo sleep variables (changes are often reported anecdotally), and possibly other things such as my daily self-ratings or extracted factors. I used 90-day blocks because that is long enough for effects to manifest (~12 weeks) and conveniently matches up with the pill count in each Swanson bottle:
Baseline/off (A): prior 90 days: 2014-06-28–2014-09-2512ya
On (B): 2014-09-26–2014-12-1912ya
Off (A): 2014-12-20–2015-03-1911ya
On (B): 2015-03-20–2015-06-0511ya
End/Off (A): 2015-06-06–2015-09-0411ya
The quasi-experiment went reasonably well and I noticed no side-effects or visible changes.
Data Prep
Daily ratings:
mp <- na.omit(read.csv("~/selfexperiment/mp.csv", colClasses=c("Date", "integer")))(I am not using any productivity factors which might improve substantially on my MP self-ratings because in the analyses I try periodically with a large set of variables eg. Git commits & number of emails sent, as of May 2018, I still haven’t found any clear ‘productivity’ factor, to my disappointment.)
Query Mnemosyne spaced repetition logs (see Treadmill), get grades recorded each day (which reflects memory retrieval that day) and the next future grade for each card (reflects memory encoding/increase in memorization that day), along with ‘easiness’ and hour/day covariates; then fit a Bayesian multilevel model with random effects for each card and day regressing on current & future grade; finally, extract the two random-effects for each day and sum them to get an index variable of my memory performance that day:
target <- "~/doc/mnemosyne/default.db"
library(sqldf)
# .schema log
# CREATE TABLE log(
# _id integer primary key autoincrement,
# event_type integer,
# timestamp integer,
# object_id text,
# grade integer,
# easiness real,
# acq_reps integer,
# ret_reps integer,
# lapses integer,
# acq_reps_since_lapse integer,
# ret_reps_since_lapse integer,
# scheduled_interval integer,
# actual_interval integer,
# thinking_time integer,
# next_rep integer,
# scheduler_data integer
# );
grades <- sqldf("SELECT timestamp,object_id,grade,easiness,thinking_time,actual_interval,(SELECT grade \
FROM log AS log2 WHERE log2.object_id = log.object_id AND log2.timestamp > log.timestamp \
ORDER BY log2.timestamp DESC LIMIT 1) AS grade_future FROM log WHERE event_type==9;",
dbname=target,
method = c("integer", "factor","integer","numeric","integer","integer", "integer"))
grades$timestamp <- as.POSIXct(grades$timestamp, origin = "1970-01-01", tz = "EST")
grades$thinking_time.log <- log1p(grades$thinking_time); grades$thinking_time <- NULL
colnames(grades) <- c("Timestamp", "ID", "Grade", "Easiness", "Interval.length", "Grade.future",
"Thinking.time.log")
## extract the temporal covariates from the timestamp
grades$WeekDay <- as.factor(weekdays(grades$Timestamp))
grades$Hour <- as.factor(as.numeric(format(grades$Timestamp, "%H")))
grades$Date <- as.Date(grades$Timestamp)
## multilevel model: mean-field variational inference rather than MCMC to avoid days of computation
library(brms)
mb <- brm(cbind(Grade,Grade.future) ~ (1|ID) + (1|Date.int) + WeekDay + Hour + Easiness, data=grades, algorithm="mean")
summary(mb)
r <- as.data.frame(ranef(mb)$Date.int)
averageGrade <- r$Estimate.Grade_Intercept + r$Estimate.Gradefuture_Intercept
dates <- as.Date(as.integer(rownames(r)), origin = "1970-01-01")
gradeDaily <- data.frame(Date=dates, Mnemosyne.performance=averageGrade)Zeo code largely borrowed from most-recent style of analysis in CO2/ZMA; for more details, see those, but the idea is to transform the variables into more Gaussian-looking variables for stabler model-fitting, specify a plausible amount of measurement error, define 2 latent variables for good and bad sleep (oddly, they don’t seem to be negations of each other), and like the Mnemosyne code, extract the latent variables for each day and sum into a single sleep quality score:
zeo <- read.csv("https://gwern.net/doc/zeo/gwern-zeodata.csv")
zeo$Date <- as.Date(sapply(strsplit(as.character(zeo$Rise.Time), " "), function(x) { x[1] }), format="%m/%d/%Y")
zeo <- subset(zeo, select=c("Date", "ZQ", "Total.Z", "Time.to.Z", "Time.in.Wake", "Time.in.REM",
"Time.in.Light", "Time.in.Deep", "Awakenings", "Morning.Feel"))
zeo$Total.Z.2 <- zeo$Total.Z^2
zeo$ZQ.2 <- zeo$ZQ^2
zeo$Time.in.REM.2 <- zeo$Time.in.REM^2
zeo$Time.in.Light.2 <- zeo$Time.in.Light^2
zeo$Time.in.Wake.log <- log1p(zeo$Time.in.Wake)
zeo$Time.to.Z.log <- log1p(zeo$Time.to.Z)
model1 <- '
## single-indicator measurement error model for each sleep variable assuming decent reliability:
ZQ.2_latent =~ 1*ZQ.2
ZQ.2 ~~ 0.7*ZQ.2
Total.Z.2_latent =~ 1*Total.Z.2
Total.Z.2 ~~ 0.7*Total.Z.2
Time.in.REM.2_latent =~ 1*Time.in.REM.2
Time.in.REM.2 ~~ 0.7*Time.in.REM.2
Time.in.Light.2_latent =~ 1*Time.in.Light.2
Time.in.Light.2 ~~ 0.7*Time.in.Light.2
Time.in.Deep_latent =~ 1*Time.in.Deep
Time.in.Deep ~~ 0.7*Time.in.Deep
Time.to.Z.log_latent =~ 1*Time.to.Z.log
Time.to.Z.log ~~ 0.7*Time.to.Z.log
Time.in.Wake.log_latent =~ 1*Time.in.Wake.log
Time.in.Wake.log ~~ 0.7*Time.in.Wake.log
Awakenings_latent =~ 1*Awakenings
Awakenings ~~ 0.7*Awakenings
GOOD_SLEEP =~ ZQ.2_latent + Total.Z.2_latent + Time.in.REM.2_latent + Time.in.Light.2_latent + Time.in.Deep_latent + Morning.Feel
BAD_SLEEP =~ Time.to.Z.log_latent + Time.in.Wake.log_latent + Awakenings_latent
'
## Fit Bayesian SEM:
library(blavaan)
s1 <- bsem(model1, n.chains=8, test="none", burnin=10000, sample=10000,
dp = dpriors(nu = "dnorm(0,1)", alpha = "dnorm(0,1)", beta = "dnorm(0,200)"),
jagcontrol=list(method="rjparallel"), fixed.x=FALSE, data=scale(zeo[-1])); summary(s1)
sleepIndex <- predict(s1)[,9] - predict(s1)[,10] # GOOD_SLEEP - BAD_SLEEP
zeo$Sleep.performance <- sleepIndexMerge the 3 datasets, restrict down to the ABABA time-range, classify by Bacopa status:
df <- merge(zeo, merge(gradeDaily, mp, all=TRUE), all=TRUE)
df <- df[!is.na(df$Date),]
df <- df[df$Date>=as.Date("2014-06-28") & df$Date<=as.Date("2015-09-04"),]
df$Date.int <- as.integer(df$Date)
df$Bacopa <- FALSE
df[df$Date>=as.Date("2014-06-28") & df$Date<=as.Date("2014-09-25"),]$Bacopa <- FALSE
df[df$Date>=as.Date("2014-09-26") & df$Date<=as.Date("2014-12-19"),]$Bacopa <- TRUE
df[df$Date>=as.Date("2014-12-20") & df$Date<=as.Date("2015-03-19"),]$Bacopa <- FALSE
df[df$Date>=as.Date("2015-03-20") & df$Date<=as.Date("2015-06-05"),]$Bacopa <- TRUE
df[df$Date>=as.Date("2015-06-06") & df$Date<=as.Date("2015-09-04"),]$Bacopa <- FALSE
write.csv(df, row.names=FALSE, file="2018-05-17-gwern-bacopa.csv")Analysis
df <- read.csv("https://gwern.net/doc/nootropic/bacopa/2018-05-17-gwern-bacopa.csv")
# Date ZQ Total.Z Time.to.Z Time.in.Wake Time.in.REM
# Min. :2014-06-28 Min. : 14.00000 Min. : 70.0000 Min. : 1.00000 Min. : 0.00000 Min. : 12.0000
# 1st Qu.:2014-10-14 1st Qu.: 85.00000 1st Qu.:496.2500 1st Qu.: 7.00000 1st Qu.: 12.00000 1st Qu.:138.0000
# Median :2015-01-30 Median : 95.00000 Median :544.0000 Median :20.00000 Median : 23.00000 Median :163.0000
# Mean :2015-01-30 Mean : 93.11521 Mean :530.2465 Mean :19.64286 Mean : 29.20507 Mean :157.4816
# 3rd Qu.:2015-05-18 3rd Qu.:103.00000 3rd Qu.:579.0000 3rd Qu.:27.00000 3rd Qu.: 37.00000 3rd Qu.:183.0000
# Max. :2015-09-04 Max. :129.00000 Max. :682.0000 Max. :95.00000 Max. :167.00000 Max. :263.0000
# NA's :1 NA's :1 NA's :1 NA's :1 NA's :1
# Time.in.Light Time.in.Deep Awakenings Morning.Feel Total.Z.2 ZQ.2 Time.in.REM.2
# Min. : 38.0000 Min. : 5.0000 Min. : 0.000000 Min. :0.000000 Min. : 4900.0 Min. : 196.000 Min. : 144.00
# 1st Qu.:292.0000 1st Qu.: 48.0000 1st Qu.: 4.000000 1st Qu.:2.000000 1st Qu.:246264.2 1st Qu.: 7225.000 1st Qu.:19044.00
# Median :317.0000 Median : 57.0000 Median : 6.000000 Median :3.000000 Median :295936.0 Median : 9025.000 Median :26569.00
# Mean :313.9516 Mean : 59.3318 Mean : 6.341014 Mean :2.562212 Mean :287184.9 Mean : 8915.078 Mean :26341.23
# 3rd Qu.:344.7500 3rd Qu.: 69.0000 3rd Qu.: 8.000000 3rd Qu.:3.000000 3rd Qu.:335241.0 3rd Qu.:10609.000 3rd Qu.:33489.00
# Max. :459.0000 Max. :142.0000 Max. :16.000000 Max. :4.000000 Max. :465124.0 Max. :16641.000 Max. :69169.00
# NA's :1 NA's :1 NA's :1 NA's :1 NA's :1 NA's :1 NA's :1
# Time.in.Light.2 Time.in.Wake.log Time.to.Z.log Sleep.performance Mnemosyne.performance MP
# Min. : 1444.0 Min. :0.000000 Min. :0.6931472 Min. :-1.8207928 Min. :-0.81207471 Min. :1.000000
# 1st Qu.: 85264.0 1st Qu.:2.564949 1st Qu.:2.0794415 1st Qu.:-0.1382757 1st Qu.:-0.08138984 1st Qu.:3.000000
# Median :100489.0 Median :3.178054 Median :3.0445224 Median : 0.2507222 Median : 0.02087041 Median :3.000000
# Mean :100831.6 Mean :3.091542 Mean :2.6811233 Mean : 0.2215090 Mean : 0.00790124 Mean :3.262069
# 3rd Qu.:118852.8 3rd Qu.:3.637586 3rd Qu.:3.3322045 3rd Qu.: 0.6038839 3rd Qu.: 0.12563885 3rd Qu.:4.000000
# Max. :210681.0 Max. :5.123964 Max. :4.5643482 Max. : 1.8661274 Max. : 1.68682336 Max. :4.000000
# NA's :1 NA's :1 NA's :1 NA's :1 NA's :77
# Date.int Bacopa
# Min. :16249.0 Mode :logical
# 1st Qu.:16357.5 FALSE:271
# Median :16465.0 TRUE :164
# Mean :16465.4 NA's :0
# 3rd Qu.:16573.5
# Max. :16682.0
cor(subset(df, select=c("Sleep.performance", "Mnemosyne.performance", "MP", "Bacopa")), use="pairwise.complete.obs")
# Sleep.performance Mnemosyne.performance MP Bacopa
# Sleep.performance 1.000000000000
# Mnemosyne.performance -0.008373508585 1.000000000000
# MP 0.019296978791 0.029580496779 1.00000000000
# Bacopa -0.013829613334 -0.083324462060 -0.02286848706 1.00000000000
library(gridExtra)
p1 <- qplot(Date, Mnemosyne.performance, color=Bacopa, data=df) + stat_smooth()
p2 <- qplot(Date, MP, color=Bacopa, data=df) + stat_smooth()
p3 <- qplot(Date, Sleep.performance, color=Bacopa, data=df) + stat_smooth()
grid.arrange(p1, p2, p3, ncol=1)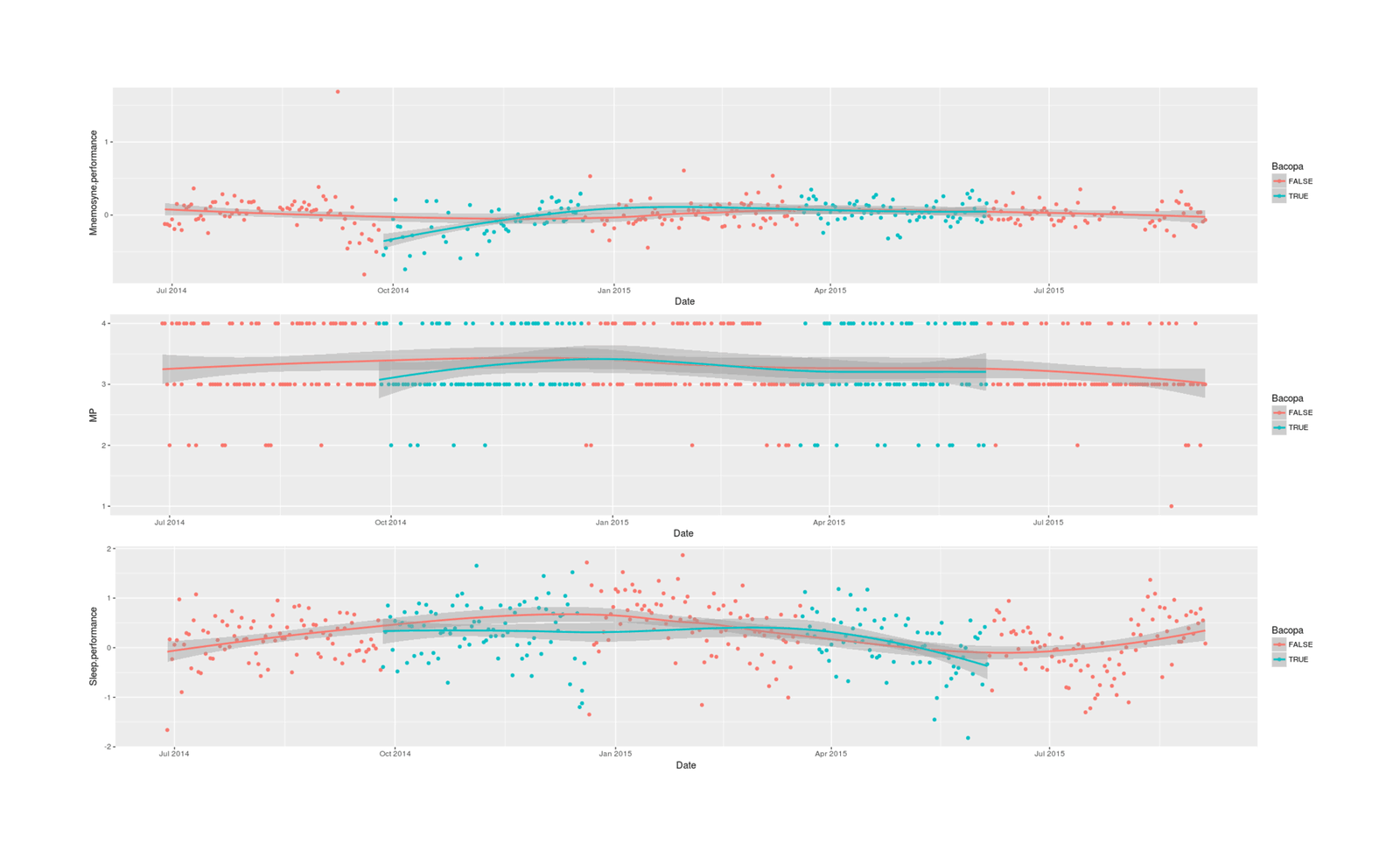
Graph of daily sleep, memory, and productivity self-ratings over time during Bacopa quasi-experiment
For analysis, the baseline linear model and then a Bayesian model with a B-spline to model the time-series/autocorrelation aspect2:
summary(lm(cbind(Mnemosyne.performance, Sleep.performance, MP) ~ Bacopa, data=df))
# Response Mnemosyne.performance :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.02091904 0.01377171 1.51899 0.12966
# BacopaTRUE -0.03534109 0.02256296 -1.56633 0.11816
#
# Residual standard error: 0.2061161 on 355 degrees of freedom
# (78 observations deleted due to missingness)
# Multiple R-squared: 0.00686354, Adjusted R-squared: 0.004065972
# F-statistic: 2.453396 on 1 and 355 DF, p-value: 0.1181619
#
# Response Sleep.performance :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.24477449 0.03711767 6.59455 1.5485e-10
# BacopaTRUE -0.06054636 0.06081197 -0.99563 0.32011
#
# Residual standard error: 0.5555265 on 355 degrees of freedom
# (78 observations deleted due to missingness)
# Multiple R-squared: 0.002784573, Adjusted R-squared: -2.44843e-05
# F-statistic: 0.9912838 on 1 and 355 DF, p-value: 0.320107
#
# Response MP :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 3.29464286 0.04072128 80.90716 < 2e-16
# BacopaTRUE -0.03900376 0.06671595 -0.58462 0.55917
#
# Residual standard error: 0.6094603 on 355 degrees of freedom
# (78 observations deleted due to missingness)
# Multiple R-squared: 0.0009618499, Adjusted R-squared: -0.001852342
# F-statistic: 0.3417855 on 1 and 355 DF, p-value: 0.5591718
bacopa <- brm(cbind(Mnemosyne.performance, Sleep.performance, MP) ~ s(Date.int) + Bacopa, data=df); summary(bacopa)
# Family: MV(gaussian, gaussian, gaussian)
# Links: mu = identity; sigma = identity
# mu = identity; sigma = identity
# mu = identity; sigma = identity
# Formula: Mnemosyne.performance ~ s(Date.int) + Bacopa
# Sleep.performance ~ s(Date.int) + Bacopa
# MP ~ s(Date.int) + Bacopa
# Data: df (Number of observations: 357)
# Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
# total post-warmup samples = 4000
#
# Smooth Terms:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sds(Mnemosyneperformance_sDate.int_1) 3.44 1.19 1.79 6.52 914 1.00
# sds(Sleepperformance_sDate.int_1) 3.30 1.43 1.24 6.89 1006 1.00
# sds(MP_sDate.int_1) 0.80 0.85 0.02 3.13 871 1.01
#
# Population-Level Effects:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# Mnemosyneperformance_Intercept -0.02 0.02 -0.05 0.02 3372 1.00
# Sleepperformance_Intercept 0.28 0.05 0.19 0.39 2946 1.00
# MP_Intercept 3.30 0.05 3.22 3.39 4000 1.00
# Mnemosyneperformance_BacopaTRUE 0.07 0.05 -0.02 0.16 3097 1.00
# Mnemosyneperformance_sDate.int_1 0.63 0.21 0.23 1.05 2168 1.00
# Sleepperformance_BacopaTRUE -0.16 0.11 -0.40 0.04 2461 1.00
# Sleepperformance_sDate.int_1 1.23 0.47 0.39 2.21 1697 1.00
# MP_BacopaTRUE -0.07 0.08 -0.23 0.09 4000 1.00
# MP_sDate.int_1 -0.15 0.23 -0.72 0.24 1444 1.00
#
# Family Specific Parameters:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sigma_Mnemosyneperformance 0.19 0.01 0.17 0.20 4000 1.00
# sigma_Sleepperformance 0.52 0.02 0.48 0.56 4000 1.00
# sigma_MP 0.61 0.02 0.57 0.66 4000 1.00
# rescor(Mnemosyneperformance,Sleepperformance) -0.00 0.05 -0.11 0.10 4000 1.00
# rescor(Mnemosyneperformance,MP) 0.02 0.05 -0.09 0.12 4000 1.00
# rescor(Sleepperformance,MP) -0.01 0.05 -0.11 0.09 4000 1.00
mean(posterior_samples(bacopa, "Mnemosyneperformance_BacopaTRUE")[,1] > 0)
# [1] 0.93025
mean(posterior_samples(bacopa, "Sleepperformance_BacopaTRUE")[,1] < 0)
# [1] 0.94525
mean(posterior_samples(bacopa, "MP_BacopaTRUE")[,1] < 0)
# [1] 0.803Unsurprisingly given a de facto sample size n = 5 due to the long-term chronic effects forcing a small ABABA quasi-experimental design, the results are largely inconclusive; using multilevel Mnemosyne scores and latent sleep indexes can help reduce measurement error but can only do so much.
The strongest result, in terms of posterior probability of a nonzero correlation between Bacopa & the 3 variables, is, perhaps as one would predict based on the Bacopa literature, on my Mnemosyne memory performance: a 0.07 (95% credible interval: -0.02-0.16) SD increase in retention, P = 0.93. If real & causal, that would be a small effect, but perhaps worthwhile in some contexts like medical school cramming (especially since it comes on top of an already quite powerful memory enhancement intervention - spaced repetition). The other two estimated correlations, unfortunately, are negative and also of similar posterior probability (P = 0.95, P = 0.80).
Conclusion
So on net, I’d say the results neither encourage nor discourage Bacopa use and are uninformative mostly as I expected due to the small sample size and difficulty of distinguishing any temporal trends from actual Bacopa effects. Given the difficulty of investigating Bacopa, it probably isn’t worthwhile to try to experiment further with a randomized blinded self-experiment because it would require extremely long time investments.
This is calculated assuming Vitacost is still offering the 2-for-1 sale which it was on 2014-09-26.↩︎
In the past I’ve used
bstswithbrmsfor time-series, but the author now strongly discourages its use, saying it is integrated intobrmsin an ad hoc and unmaintainable matter and thinks splines are a better approach in general, so I’ve switched over although I’m not as familiar with Bayesian splines as I’d like.↩︎