The Problem

Most scientifically-inclined people are reasonably aware that one of the major divides in research is that correlation ≠ causation: that having discovered some relationship between various data X and Y (not necessarily Pearson’s r, but any sort of mathematical or statistical relationship, whether it be a humble r or an opaque deep neural network’s predictions), we do not know how Y would change if we manipulated X. Y might increase, decrease, do something complicated, or remain implacably the same.

Correlations Often Aren’t

This might be because the correlation is not a real one, and is spurious, in the sense that it would disappear if we gathered more data, and was an illusory correlation due to biases; or it could be an artifact of our mathematical procedures as in “spurious correlations”; or it is a Type I error, a correlation thrown up by the standard statistical problems we all know about, such as too-small n, false positives from sampling error (A & B just happened to sync together due to randomness), data-mining/multiple testing, p-hacking, data snooping, selection bias, publication bias, misconduct, inappropriate statistical tests, etc. The Replication Crisis has seriously shaken faith in the published research literature in many fields, and it’s clear that many correlations are over-estimated in strength by severalfold, or the sign is in fact the opposite direction.

Correlation Often Isn’t Causation

I’ve read about those problems at length, and despite knowing about all that, there still seems to be a problem: I don’t think those issues explain away all the correlations which turn out to be confounds—correlation too often ≠ causation.

But let’s say we get past that and we have established beyond a reasonable doubt that some X and Y really do correlate. We still have not solved the problem.

Shouldn’t It Be Easy?

We’d expect that the a priori odds are good, by the principle of indifference: 1⁄3! After all, you can divvy up the possibilities as:

1. A causes B (A → B)

2. B causes A (A ← B)

3. both A and B are caused by C (A ← C → B)

   (Possibly in a complex way like Berkson’s paradox or conditioning on unmentioned variables, like a phone-based survey inadvertently generating conclusions valid only for the phone-using part of the population, causing amusing pseudo-correlations.)

If it’s either #1 or #2, we’re good and we’ve found a causal relationship; it’s only outcome #3 which leaves us baffled & frustrated. If we were guessing at random, you’d expect us to still be right at least 33% of the time. (As in the joke about the lottery—you’ll either win or lose, and you don’t know which, so it’s 50-50, and you like dem odds!) And we can draw on all sorts of knowledge to do better.³

I think a lot of people tend to put a lot of weight on any observed correlation because of this intuition that a causal relationship is normal & probable because, well, “how else could this correlation happen if there’s no causal connection between A & B‽” And fair enough—there’s no grand cosmic conspiracy arranging matters to fool us by always putting in place a C factor to cause scenario #3, right? If you question people, of course they know correlation doesn’t necessarily mean causation—everyone knows that—since there’s always a chance of a lurking confound, and it would be great if you had a randomized experiment to draw on; but you think with the data you have, not the data you wish you had, and can’t let the perfect be the enemy of the better. So when someone finds a correlation between A and B, it’s no surprise that suddenly their language & attitude change and they seem to place great confidence in their favored causal relationship even if they piously acknowledge “Yes, correlation is not causation, but… obviously hanging out with fat people will make you fat / parents influence their kids a lot eg. smoking encourages their kids to smoke / when we gave babies a new drug, fewer went blind / female-named hurricanes increase death tolls due to sexistly underestimating women / Kaposi’s sarcoma correlates so highly with AIDS that it must be another consequence of HIV (actually caused by HHV-8 which is transmitted simultaneously with HIV) / vitamin and anti-oxidant use (among many other lifestyle choices) will save lives / LSD & marijuana use associates with and thus surely causes schizophrenia and other forms of insanity (despite increases in marijuana use not followed by any schizophrenia increases) / hormone replacement therapy correlates with mortality reduction in women so it definitely helps and doesn’t hurt” etc.

Besides the intuitiveness of correlation=causation, we are also desperate and want to believe: correlative data is so rich and so plentiful, and experimental data so rare. If it is not usually the case that correlation=causation, then what exactly are we going to do for decisions and beliefs, and what exactly have we spent all our time to obtain? When I look at some dataset with a number of variables and I run a multiple regression and can report that variables A, B, and C are all statistically-significant and of large effect-size when regressed on D, all I have really done is learned something along the lines of “in a hypothetical dataset generated in the exact same way, if I somehow was lacking data on D, I could make a better prediction in a narrow mathematical sense of no importance (squared error) based on A/B/C”. I have not learned whether A/B/C cause D, or whether I could predict values of D in the future, or anything about how I could intervene and manipulate any of A-D, or anything like that—rather, I have learned a small point about prediction. To take a real example: when I learn that moderate alcohol consumption means the actuarial prediction of lifespan for drinkers should be increased slightly, why on earth would I care about this at all unless it was causal? When epidemiologists emerge from a huge survey reporting triumphantly that steaks but not egg consumption slightly predicts decreased lifespan, why would anyone care aside from perhaps life insurance companies? Have you ever been abducted by space aliens and ordered as part of an inscrutable alien blood-sport to take a set of data about Midwest Americans born 1960^–₉1969_55ya with dietary predictors you must combine linearly to create predictors of heart attacks under a squared error loss function to outpredict your fellow abductees from across the galaxy? Probably not. Why would anyone give them grant money for this, why would they spend their time on this, why would they read each others’ papers unless they had a “quasi-religious faith”⁴ that these correlations were more than just some coefficients in a predictive model—that they were causal? To quote Rutter2007, most discussions of correlations fall into two equally problematic camps:

…all behavioral scientists are taught that statistically significant correlations do not necessarily mean any kind of causative effect. Nevertheless, the literature is full of studies with findings that are exclusively based on correlational evidence. Researchers tend to fall into one of two camps with respect to how they react to the problem.

1. First, there are those who are careful to use language that avoids any direct claim for causation, and yet, in the discussion section of their papers, they imply that the findings do indeed mean causation.

2. Second, there are those that completely accept the inability to make a causal inference on the basis of simple correlation or association and, instead, take refuge in the claim that they are studying only associations and not causation. This second, “pure” approach sounds safer, but it is disingenuous because it is difficult to see why anyone would be interested in statistical associations or correlations if the findings were not in some way relevant to an understanding of causative mechanisms.

So, correlations tend to not be causation because it’s almost always #3, a shared cause. This commonness is contrary to our expectations, based on a simple & unobjectionable observation that of the 3 possible relationships, 2 are causal; and so we often reason as though correlation were strong evidence for causation. This leaves us with a paradox: experimental results seem to contradict intuition. To resolve the paradox, I need to offer a clear account of why shared causes/confounds are so common, and hopefully motivate a different set of intuitions.

What a Tangled Net We Weave When First We Practice to Believe

Here’s where Bayes nets & causal networks (seen previously on LW & Michael Nielsen) come up. Even simulating the simplest possible model of linear regression, adding covariates barely increase the probability of correctly inferring direction of causality, and the effect sizes remain badly imprecise (Walker2014). And when networks are inferred on real-world data, they look gnarly: tons of nodes, tons of arrows pointing all over the place. Daphne Koller early on in her Probabilistic Graphical Models course shows an example from a medical setting where the network has like 600 nodes and you can’t understand it at all. When you look at a biological causal network like metabolism:

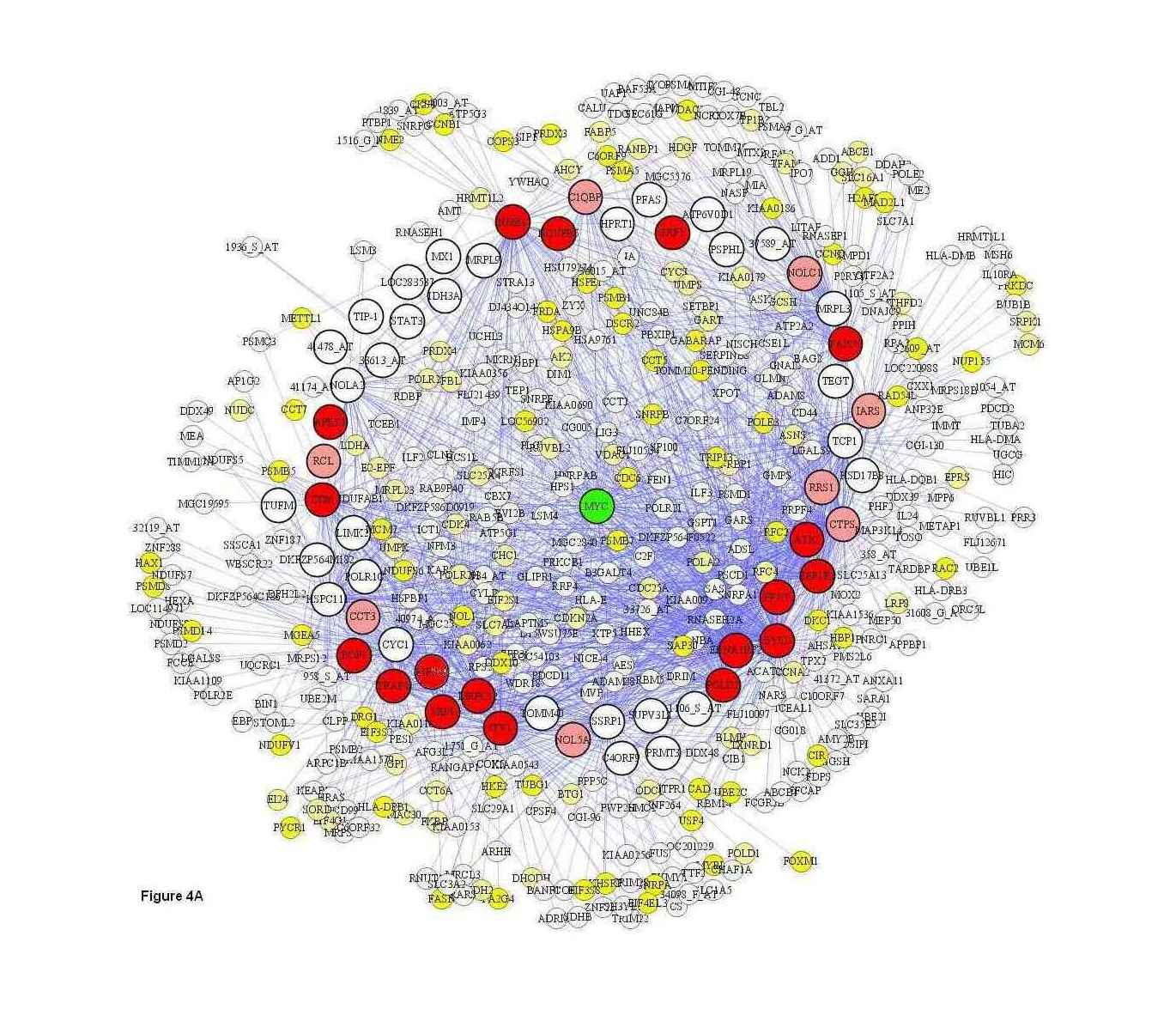
You start to appreciate how everything might be correlated with everything, but (usually) not cause each other.

This is not too surprising if you step back and think about it: life is complicated, we have limited resources, and everything has a lot of moving parts. (How many discrete parts does an airplane have? Or your car? Or a single cell? Or think about a chess player analyzing a position: ‘if my bishop goes there, then the other pawn can go here, which opens up a move there or here, but of course, they could also do that or try an en passant in which case I’ll be down in material but up on initiative in the center, which causes an overall shift in tempo…’) Fortunately, these networks are still simple compared to what they could be, since most nodes aren’t directly connected to each other, which tamps down on the combinatorial explosion of possible networks. (How many different causal networks are possible if you have 600 nodes to play with? The exact answer is complicated but it’s much larger than 2⁶⁰⁰—so very large!)

One interesting thing I managed to learn from PGM (before concluding it was too hard for me and I should try it later) was that in a Bayes net even if two nodes were not in a simple direct correlation relationship A → B, you could still learn a lot about A from setting B to a value, even if the two nodes were ‘way across the network’ from each other. You could trace the influence flowing up and down the pathways to some surprisingly distant places if there weren’t any blockers.

The bigger the network, the more possible combinations of nodes to look for a pairwise correlation between them (eg. If there are 10 nodes/variables and you are looking at bivariate correlations, then you have 10 choose 2 = 45 possible comparisons, and with 20, 190, and 40, 780. 40 variables is not that much for many real-world problems.) A lot of these combos will yield some sort of correlation. But does the number of causal relationships go up as fast? I don’t think so (although I can’t prove it).

If not, then as causal networks get bigger, the number of genuine correlations will explode but the number of genuine causal relationships will increase slower, and so the fraction of correlations which are also causal will collapse.

(Or more concretely: suppose you generated a randomly connected causal network with x nodes and y arrows perhaps using the algorithm in Kuipers & Moffa2012, where each arrow has some random noise in it; count how many pairs of nodes are in a causal relationship; now, n times initialize the root nodes to random values and generate a possible state of the network & storing the values for each node; count how many pairwise correlations there are between all the nodes using the n samples (using an appropriate significance test & alpha if one wants); divide # of causal relationships by # of correlations, store; return to the beginning and resume with x+1 nodes and y+1 arrows… As one graphs each value of x against its respective estimated fraction, does the fraction head toward 0 as x increases? My thesis is it does. Or, since there must be at least as many causal relationships in a graph as there are arrows, you could simply use that as an upper bound on the fraction.)

It turns out, we weren’t supposed to be reasoning ‘there are 3 categories of possible relationships, so we start with 33%’, but rather: ‘there is only one explanation “A causes B”, only one explanation “B causes A”, but there are many explanations of the form “C₁ causes A and B”, “C₂ causes A and B”, “C₃ causes A and B”…’, and the more nodes in a field’s true causal networks (psychology or biology vs physics, say), the bigger this last category will be.

The real world is the largest of causal networks, so it is unsurprising that most correlations are not causal, even after we clamp down our data collection to narrow domains. Hence, our prior for “A causes B” is not 50% (it’s either true or false) nor is it 33% (either A causes B, B causes A, or mutual cause C) but something much smaller: the number of causal relationships divided by the number of pairwise correlations for a graph, which ratio can be roughly estimated on a field-by-field basis by looking at existing work or directly for a particular problem (perhaps one could derive the fraction based on the properties of the smallest inferrable graph that fits large datasets in that field). And since the larger a correlation relative to the usual correlations for a field, the more likely the two nodes are to be close in the causal network and hence more likely to be joined causally, one could even give causality estimates based on the size of a correlation (eg. an r = 0.9 leaves less room for confounding than an r of 0.1, but how much will depend on the causal network).

This is exactly what we see. How do you treat cancer? Thousands of treatments get tried before one works. How do you deal with poverty? Most programs are not even wrong. Or how do you fix societal woes in general? Most attempts fail miserably and the higher-quality your studies, the worse attempts look (leading to Rossi’s Metallic Rules). This even explains why ‘everything correlates with everything’ and Andrew Gelman’s dictum about how coefficients are never zero: the reason large datasets find most of their variables to have non-zero correlations (often reaching statistical-significance) is because the data is being drawn from large complicated causal networks in which almost everything really is correlated with everything else.

And thus I was enlightened.

Comment

Since I know so little about causal modeling, I asked our local causal researcher Ilya Shpitser to maybe leave a comment about whether the above was trivially wrong / already-proven / well-known folklore / etc; for convenience, I’ll excerpt the core of his comment:

But does the number of causal relationships go up just as fast? I don’t think so (although at the moment I can’t prove it).

I am not sure exactly what you mean, but I can think of a formalization where this is not hard to show. We say A “structurally causes” B in a DAG G if and only if there is a directed path from A to B in G. We say A is “structurally dependent” with B in a DAG G if and only if there is a marginal d-connecting path from A to B in G.

A marginal d-connecting path between two nodes is a path with no consecutive edges of the form * → * ← * (that is, no colliders on the path). In other words all directed paths are marginal d-connecting but the opposite isn’t true.

The justification for this definition is that if A “structurally causes” B in a DAG G, then if we were to intervene on A, we would observe B change (but not vice versa) in “most” distributions that arise from causal structures consistent with G. Similarly, if A and B are “structurally dependent” in a DAG G, then in “most” distributions consistent with G, A and B would be marginally dependent (eg. what you probably mean when you say ‘correlations are there’).

I qualify with “most” because we cannot simultaneously represent dependences and independences by a graph, so we have to choose. People have chosen to represent independences. That is, if in a DAG G some arrow is missing, then in any distribution (causal structure) consistent with G, there is some sort of independence (missing effect). But if the arrow is not missing we cannot say anything. Maybe there is dependence, maybe there is independence. An arrow may be present in G, and there may still be independence in a distribution consistent with G. We call such distributions “unfaithful” to G. If we pick distributions consistent with G randomly, we are unlikely to hit on unfaithful ones (subset of all distributions consistent with G that is unfaithful to G has measure zero), but Nature does not pick randomly… so unfaithful distributions are a worry. They may arise for systematic reasons (maybe equilibrium of a feedback process in bio?)

If you accept above definition, then clearly for a DAG with n vertices, the number of pairwise structural dependence relationships is an upper bound on the number of pairwise structural causal relationships. I am not aware of anyone having worked out the exact combinatorics here, but it’s clear there are many many more paths for structural dependence than paths for structural causality.

---

But what you actually want is not a DAG with n vertices, but another type of graph with n vertices. The “Universe DAG” has a lot of vertices, but what we actually observe is a very small subset of these vertices, and we marginalize over the rest. The trouble is, if you start with a distribution that is consistent with a DAG, and you marginalize over some things, you may end up with a distribution that isn’t well represented by a DAG. Or “DAG models aren’t closed under marginalization.”

That is, if our DAG is A → B ← H → C ← D, and we marginalize over H because we do not observe H, what we get is a distribution where no DAG can properly represent all conditional independences. We need another kind of graph.

In fact, people have come up with a mixed graph (containing → arrows and ⟺ arrows) to represent margins of DAGs. Here → means the same as in a causal DAG, but ⟺ means “there is some sort of common cause/confounder that we don’t want to explicitly write down.” Note: ⟺ is not a correlative arrow, it is still encoding something causal (the presence of a hidden common cause or causes). I am being loose here—in fact it is the absence of arrows that means things, not the presence.

I do a lot of work on these kinds of graphs, because these are graphs are the sensible representation of data we typically get—drawn from a marginal of a joint distribution consistent with a big unknown DAG.

But the combinatorics work out the same in these graphs—the number of marginal d-connected paths is much bigger than the number of directed paths. This is probably the source of your intuition. Of course what often happens is you do have a (weak) causal link between A and B, but a much stronger non-causal link between A and B through an unobserved common parent. So the causal link is hard to find without “tricks.”

Shouting 2+2=4 From the Rooftops

To go on a tangent: why is it so important that we hammer this in?

The unreliability is bad enough, but I’m also worried that the knowledge correlation ≠ causation, one of the core ideas of the scientific method and fundamental to fields like modern medicine, is going underappreciated and is being abandoned by meta-contrarians due to its inconvenience. Pointing it out is “nothing helpful” or “meaningless”, and justified skepticism is actually just “a dumb-ass thing to say”, a “statistical cliché that closes threads and ends debates, the freshman platitude turned final shutdown” often used by “party poopers” “Internet blowhards” to serve an “agenda” & is sometimes “a dog whistle”; in practice, such people seem to go well beyond the XKCD comic and proceed to take any correlations they like as strong evidence for causation, and any disagreement is an unsophisticated middlebrow dismissal & denialism.

So it’s unsurprising that one so often runs into researchers for whom indeed correlation=causation (we certainly wouldn’t want to be freshmen or Internet blowhards, would we?). It is common to use causal language and make recommendations (Prasad et al 2013), but even if they don’t, you can be sure to see them confidently talking causally to other researchers or journalists or officials. (I’ve noticed this sort of constant motte-and-bailey slide from vague mentions of how results are correlative tucked away at the end of the paper to freely dispensing advice for policymakers about how their research proves X should be implemented is particularly common in medicine, sociology, and education.)

Bandying phrases with meta-contrarians won’t help much here; I agree with them that correlation ought to be some evidence for causation. eg if I suspect that A → B, and I collect data and establish beyond doubt that A&B correlates r = 0.7, surely this observation, which is consistent with my theory, should boost my confidence in my theory, just as an observation like r = 0.0001 would trouble me greatly. But how much…?

As it is, it seems we fall readily into intellectual traps of our own making. When you believe every correlation adds support to your causal theory, you just get more and more wrong as you collect more data.

Heuristics & Biases

Now assuming the foregoing to be right (which I’m not sure about; in particular, I’m dubious that correlations in causal nets really do increase much faster than causal relations do), what’s the psychology of this? I see a few major ways that people might be incorrectly reasoning when they overestimate the evidence given by a correlation:

• they might be aware of the imbalance between correlations and causation, but underestimate how much more common correlation becomes compared to causation.

  This could be shown by giving causal diagrams and seeing how elicited probability changes with the size of the diagrams: if the probability is constant, then the subjects would seem to be considering the relationship in isolation and ignoring the context.

  It might be remediable by showing a network and jarring people out of a simplistic comparison approach.

• they might not be reasoning in a causal-net framework at all, but starting from the naive 33% base-rate you get when you treat all 3 kinds of causal relationships equally.

  This could be shown by eliciting estimates and seeing whether the estimates tend to look like base rates of 33% and modifications thereof.

  Sterner measures might be needed: could we draw causal nets with not just arrows showing influence but also another kind of arrow showing correlations? For example, the arrows could be drawn in black, inverse correlations drawn in red, and regular correlations drawn in green. The picture would be rather messy, but simply by comparing how few black arrows there are to how many green and red ones, it might visually make the case that correlation is much more common than causation.

• alternately, they may really be reasoning causally and suffer from a truly deep & persistent cognitive illusion that when people say ‘correlation’ it’s really a kind of causation and don’t understand the technical meaning of ‘correlation’ in the first place (which is not as unlikely as it may sound, given examples like David Hestenes’s demonstration of the persistence of Aristotelian folk-physics in physics students as all they had learned was guessing passwords; on the test used, see eg. Halloun & Hestenes1985 & Hestenes et al 1992); in which cause it’s not surprising that if they think they’ve been told a relationship is ‘causation’, then they’ll think the relationship is causation. Ilya remarks:

  Pearl has this hypothesis that a lot of probabilistic fallacies/paradoxes/biases are due to the fact that causal and not probabilistic relationships are what our brain natively thinks about. So eg. Simpson’s paradox is surprising because we intuitively think of a conditional distribution (where conditioning can change anything!) as a kind of “interventional distribution” (no Simpson’s type reversal under interventions: “Understanding Simpson’s Paradox”, Pearl2014 [see also Pearl’s comments on Nielsen’s blog)).

  This hypothesis would claim that people who haven’t looked into the math just interpret statements about conditional probabilities as about “interventional probabilities” (or whatever their intuitive analogue of a causal thing is).

  This might be testable by trying to identify simple examples where the two approaches diverge, similar to Hestenes’s quiz for diagnosing belief in folk-physics.

Everything Correlates With Everything

Main article: “Everything Is Correlated”.